机械手不同抓取控制方式对番茄机械损伤的影响分析

周 俊 孟一猛 张 娜 严正红

(南京农业大学江苏省智能化农业装备重点实验室， 南京 210031)

机械手不同抓取控制方式对番茄机械损伤的影响分析

周 俊 孟一猛 张 娜 严正红

(南京农业大学江苏省智能化农业装备重点实验室， 南京 210031)

为了分析机械手不同抓取控制方式对番茄造成的机械损伤。通过Burgers粘弹性模型描述番茄的变形特征，利用蠕变实验获得番茄样本的粘弹性参数。选择匀减速、先匀速后减速以及变减速作为3种典型的抓取控制方式，并利用一次函数、巴特沃斯幅度平方函数和指数函数3种函数曲线描述末端执行器实际抓取过程中不同抓取控制方式的速度变化。在此基础上，对番茄塑性变形进行求解，分析在抓取时间一定时，不同抓取控制方式下番茄的塑性变形规律，并以最小塑性变形为依据，确定最优的抓取策略。结果表明：抓取控制方式3为最优抓取控制方式，当抓取速度v0=1 mm/s，抓取时间t0=1 s时，产生的最小塑性变形最小，红熟前期和红熟中期番茄的最小塑性变形分别为0.002 6 mm和0.009 8 mm。以抓取控制方式3进行抓取控制实验，实验数据和理论数据的吻合度较高，决定系数R2为0.99，验证了抓取控制方式3作为最优抓取控制方式的合理性和可行性，为优化机械手抓取过程提供了参考。

番茄； 采摘； 机械手； 抓取控制方式； 机械损伤

引言

应用农业机器人完成果蔬采摘、分拣等作业的研究越来越多[1-2]，末端执行器抓取果蔬对象是其中一个重要的作业环节。末端执行器抓取果实方式不同，对果实产生的机械损伤程度也不尽相同。在抓取过程中，果实因受到挤压、冲击、振动等多种载荷作用而产生变形，主要形成以塑性变形为主的现时损伤和以粘弹性变形为主的延迟损伤[3]，而其中塑性变形对果品品质的影响最为关键[4]。大多数的果实为粘弹性体，具有固体和流体的双重特性[5]，利用粘弹性模型及参数对果实的变形进行分析，可以为加工与采收机械的设计提供理论基础，也可以减少与控制作业过程中的机械损伤，为提高产品质量提供技术支持。

目前国内外学者已通过多种方式对抓取过程中果实的变形损伤进行研究。LI等[6]对同一番茄的不同部位进行抓取试验，对比不同抓取位置产生的峰值力和最大变形，为减少机器人抓取的机械损伤提供依据。AHMADI等[7]建立了苹果的非线性粘弹性模型，通过仿真获得不同抓取速度下苹果与刚性平板接触过程中的变形随时间的变化规律。HIGASHIMORI等[8]基于获得流变物体的四单元粘弹性模型参数分析施加的抓取力与变形之间的关系，在避免对象过度变形的条件下减少夹持作业时间。文献[9-10]利用有限元的方法分别对苹果和柑橘与不同指面类型的夹持手指的接触进行了研究，对比自动抓取过程中不同指面类型作用下接触应力和果实变形的差异。刘继展等[11]以果实的粘弹性模型为基础，研究了抓取速度与碰撞峰值力和变形之间的关系，为实现果实快速夹持作业提供借鉴。马晓丽等[12]对杨梅果开展压缩试验，结合力-变形关系曲线对其力学特性进行分析，探讨机械采摘条件下杨梅果的机械损伤机理。

但现有研究中依据塑性变形这一影响果品品质的关键因素来分析机械手抓取果蔬所造成的机械损伤的研究较为少见。因此，本文以番茄为作业对象，利用Burgers粘弹性模型表征其压缩变形特征。通过蠕变实验获得番茄样本的粘弹性参数，对3种典型抓取控制方式下果实的塑性变形进行理论分析，并依据最小塑性变形原则确定最优抓取控制方式，以期减少机械手在抓取过程中对果实产生的机械损伤。

1 番茄抓取塑性变形

对于固体农业物料的果蔬而言，可将其受力时的形变分为弹性变形和塑性变形[8,13-14]。机械手起始抓取阶段，果蔬组织产生的初始小变形为弹性变形，但变形能够完全恢复；塑性变形指在施加的外力撤销后，不能恢复而保留下来的那部分变形，是物体无法恢复原状的一种物理现状。物体最终的形状由塑性变形直接决定，同时塑性变形也是影响果品品质的关键因素。因此，本文将塑性变形作为番茄机械损伤的衡量指标，通过分析接触产生的塑性变形来评判当前抓取控制方式的优劣，从而选择合适的抓取控制方式，减少被抓物体的机械损伤。

1.1 番茄粘弹性数学模型

包括番茄在内的农业物料大多为粘弹性体，具有流变特性。果蔬的流变特性主要研究的是果蔬在外力作用下产生的流动与变形，利用粘弹性模型描述其流变特性，可以更好地分析果蔬在受载条件下的变形特征。粘弹性模型最基本的有Maxwell模型和Kelvin模型，但对于果蔬等农业物料，利用简单的两种模型不足以较为完整地表征果蔬复杂的力学特性。将两种简单的组合方式再串联起来就形成了伯格斯模型(Burgers)，如图1所示。

图1 Burgers模型Fig.1 Burgers model

Burgers模型蠕变加载过程的微分方程为

(1)

式中D(t)——变形量，mm

t——时间，s

F0——恒定载荷，N

k1——瞬时弹性系数，N/mm

k2——延迟弹性系数，N/mm

c1——串联粘性系数，N·s/mm

c2——并联粘性系数，N·s/mm

Burgers模型可以表示瞬时弹性变形、延迟弹性变形以及永久塑性变形等多种变形，且根据前人对果品特性的研究，Burgers模型能够较好地描述果品的流变特性[15-16]。因此，本文决定采用伯格斯模型表征番茄果实的变形特征。

1.2 抓取塑性变形定义

当外力f施加在物体上时，伯格斯模型表征的番茄变形如图2所示。x、xi及fi分别表示物体的总变形、每一层变形以及弹性单元层作用力(i=1)，粘弹性平行单元层作用力(i=2)和粘性单元作用层作用力(i=3)，kh为机械手指刚度，xh为从接触到稳定抓取过程中机械手的闭合位移，则番茄受力和变形的表达式为[17]

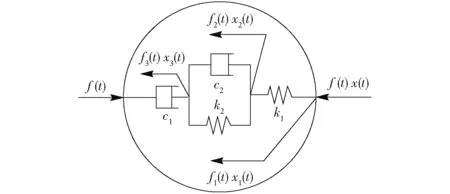
图2 番茄伯格斯模型受力变形表征Fig.2 Force-deformation characterization of Burgers model

(2)

x(t)=x1(t)

(3)

其中

f1(t)=k1(x1(t)-x2(t))

(4)

(5)

(6)

又因

x(t)=xh(t)-f(t)/kh

(7)

根据式(2)～(7)，移除fi和xi，可得抓取过程中的力-位移关系模型为

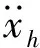
(8)

其中

B2=c1c2/k2

(9)

B1=c1

(10)

A2=c1c2(k1+kh)/(k1k2kh)

(11)

A1=[c1k1k2+kh(k1c2+k1c1+k2c1)]/(k1k2kh)

(12)

伯格斯模型表征的粘弹性物体的塑性变形主要由粘性系数c1决定[18]，则番茄的塑性变形为

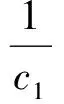
(13)

式中T——末端执行器和果实的接触时间

根据式(8)和式(13)可知，对番茄的塑性变形进行理论分析需要获得其粘弹性参数。因此，本文利用式(1)的蠕变方程，对番茄开展恒定载荷蠕变实验获得其粘弹性参数[19-21]。

2 番茄粘弹性参数获取

2.1 蠕变实验

选择番茄品种为皖粉2号的红熟前期(着红面积10%～40%)、红熟中期(着红面积40%～60%)番茄各10个，番茄的赤道直径在62～80 mm之间，质量在166～252 g之间。实验仪器包括美国FTC公司的TMS-PRO质构仪、P75型探头(直径75 mm)、工控机、游标卡尺、数显电子秤。

对各成熟期的番茄进行编号，将测试样品的果柄水平放置在质构仪上下探头间，并通过底座固定，逐一进行实验。设定探头加载速度为60 mm/min，数据采集频率为10 Hz，起始力为0.6 N，加载时间30 s。每个样品在果腰处随机选取3个样本点，并且对这3个样本点分别设定恒定压力3、5、7 N进行测试，共进行60次蠕变实验。

2.2 模型参数获取

蠕变实验可以获得番茄在恒载作用下变形随时间变化关系的蠕变曲线，利用Origin 8.0数据分析软件中的非线性拟合工具箱，通过式(1)对番茄蠕变数据进行曲线拟合，得到蠕变模型的粘弹性参数及相关系数。表1为从20个样本中随机选择2个番茄样本的粘弹性参数与相关系数，并计算其平均值。决定系数R2均高于0.992，其余样本的拟合情况与之类似，验证了所选模型的有效性。本文利用番茄样本粘弹性参数的平均值进行后续抓取控制方式的理论和仿真分析。

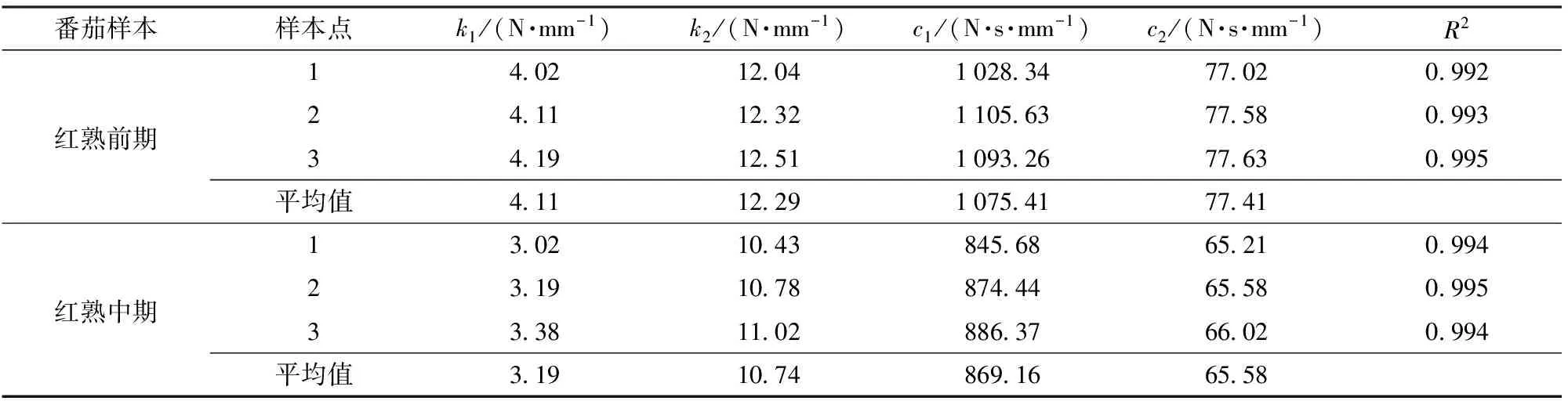
表1 粘弹性参数及决定系数Tab.1 Viscoelastic parameters and determination coefficient

3 不同抓取控制方式对塑性变形的影响

3.1 3种典型抓取控制方式

对于采摘机器人而言，在末端执行器从接触果实到停止抓取的整个阶段，末端执行器闭合速度均为从某一抓取速度最终减小为零。虽然该过程中速度变化形式存在无数种可能，但匀减速、先匀速后减速以及变减速3种方式为典型速度变化形式，即：①末端执行器以设定的抓取速度匀速闭合，接触物体后开始匀减速，直至停止。②末端执行器接触果实后，仍保持设定的抓取速度匀速闭合，一段时间后减速最终停止。③末端执行器接触果实后以加速度不断变化的方式减速运行，直至停止闭合。因此，本文选择匀减速、先匀速后减速以及变减速3种具有代表性的抓取控制方式进行分析。通常情况下人工完成单次稳定抓取动作的时间为1 s，目前，日本采摘机械手完成稳定抓取的时间大约为4 s[22]，为了分析在一定的采摘时间内，不同的抓取控制方式对果实机械损伤的影响，本节对3种典型抓取控制方式下产生的塑性变形规律进行分析，对比3种典型抓取控制方式对番茄机械损伤的影响。

结合现有实验平台(WSG 50机械手)的配置参数，选择一次函数、巴特沃斯幅度平方函数和指数函数3种函数曲线分别描述匀减速、先匀速后减速和变减速3种典型的抓取控制方式，3种函数表征的抓取速度随时间变化的关系如图3所示。

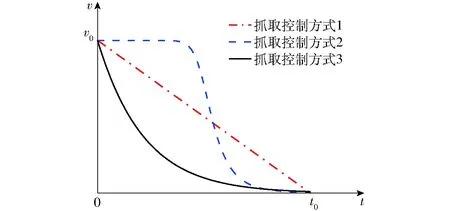
图3 3种抓取控制方式的速度随时间变化曲线Fig.3 Diagram of velocity change over time of different grasping control modes

根据实验平台的实际参数配置，确定3种典型抓取控制方式对应的速度随时间变化的函数方程为

(14)

式中v0——设定的抓取速度

v1(t)——一次函数下的速度

v2(t)——巴特沃斯幅度平方函数下的速度

v3(t)——指数函数下的速度

t0——稳定抓取时间

3.2 塑性变形理论计算

由于塑性变形是影响果品品质的关键因素，因此决定利用果实抓取过程中的塑性变形作为评判抓取控制方式优劣的依据。设定机械手抓取速度为v0，依据果实质量m，可得到当前作业对象的停止抓取力F0=mg/(2μ)(μ为摩擦因数，实验测得μ=0.22)。依据2.2节随机选取的番茄样本及其粘弹性参数平均值进行理论计算，利用式(8)、(14)进行微分方程求解获得不同抓取控制方式下番茄的受力随时间变化关系。将其代入式(13)可以获得在一定抓取时间下，不同抓取控制方式产生的塑性变形量。理论分析的数学模型求解参数如表2所示。

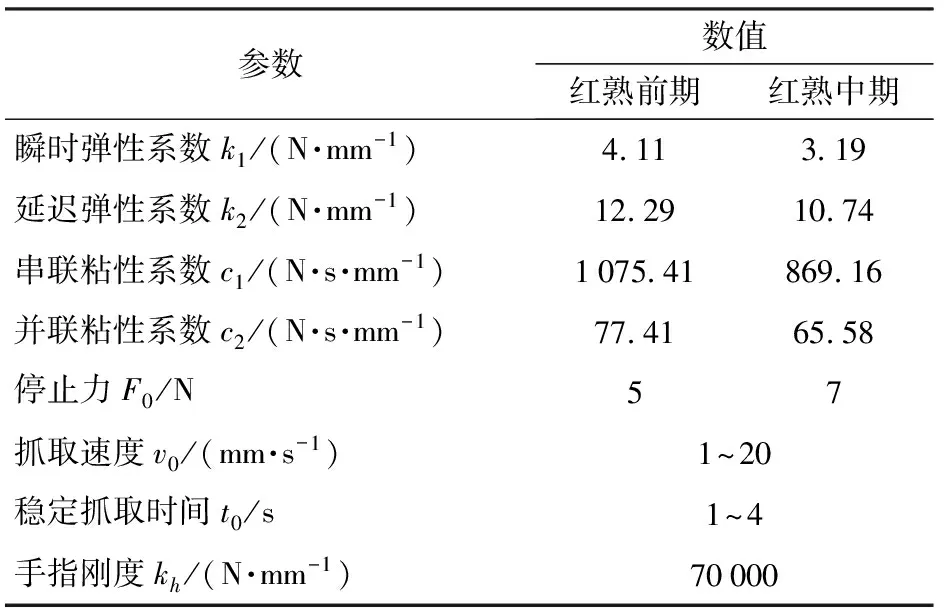
表2 模型求解参数Tab.2 Solving parameters of model

为了进一步说明求解过程，本文以抓取控制方式1在抓取速度v0=1 mm/s，t0=1 s时的抓取过程为例，对红熟前期番茄样本塑性变形的理论分析过程进行详细介绍，求解步骤如下：

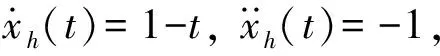
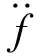
(15)

(2)式(15)为二阶常系数非齐次线性微分方程，属于f(t)=eλtPm(t)的类型。由函数解的性质知，求该式的通解可以归结为求对应齐次方程

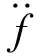
(16)

的通解和非齐次方程式(15)的一个非零特解y*。

(3)式(16)对应的特征方程为

1 648.17r2+355.47r+1=0

(17)

f*(t)=c1e-0.002 9t+c2e-0.212 8t

(18)

由于λ=0不是特征方程式(17)的根，所以应设特解为

y*=b0t+b1

(19)

将其代入式(15)，求得其1个特解为

y*=-1 075.41t+376 577.78

(20)

(4)根据机械手的稳定抓取过程参数，确定方程(15)的初始条件为：f(0)=0，f(t0)=F0，将初始条件代入式(15)求得其通解为

f(t)=-12 630e-0.002 9t-11.462 6e-0.212 8t-
1 075.41t+376 577.78

(21)

则该抓取过程对应的塑性变形表达式为

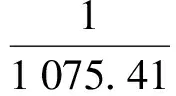
(22)

式(21)即为当番茄的粘弹性参数为k1=4.11 N/mm，k2=12.29 N/mm，c1=1 075.41 N·s/mm，c2=77.41 N·s/mm，稳定抓取时间t0=1 s，抓取速度v0=1 mm/s时，抓取控制方式1的整个稳定抓取过程中抓取力随时间的变化关系。通过Matlab仿真获得式(21)对应的力随时间变化曲线如图4所示，将式(21)代入塑性变形表达式(13)可得抓取控制方式1在该过程中的塑性变形表达式，求出对应的塑性变形Xp=0.002 7 mm。

同理，利用上述微分方程求解方法对抓取控制方式2和抓取控制方式3进行计算，得到对应的t0=1，v0=1 mm/s时的抓取力随时间变化关系如图5所示，求得对应抓取控制方式2和抓取控制方式3的塑性变形Xp分别为0.006 2、0.002 6 mm。根据以上求解过程，结合Matlab工程计算软件对不同成熟度番茄样本在通常的机械手抓取时间t0为1～4 s，抓取速度v0为1～20 mm/s情况下的塑性变形进行计算，番茄红熟前期和红熟中期的求解结果如图6和图7所示。

图6、图7为采取不同抓取控制方式，在不同抓取时间t0下，不同成熟度番茄产生的塑性变形随抓取速度的变化规律。从图6、图7中可以看出，对同一成熟度的番茄样本而言，在同一抓取时间下，随着抓取速度的增大，番茄的塑性变形增大；在不同抓取时间下，随着抓取时间的增大，机械手与番茄的接触时间延长，蠕变现象愈明显，产生的塑性变形越大。对于不同成熟度的番茄样本而言，其塑性变形随抓取速度和抓取时间的变化规律一致，且成熟度越高，相同抓取时间和抓取速度条件下产生塑性变形越大。

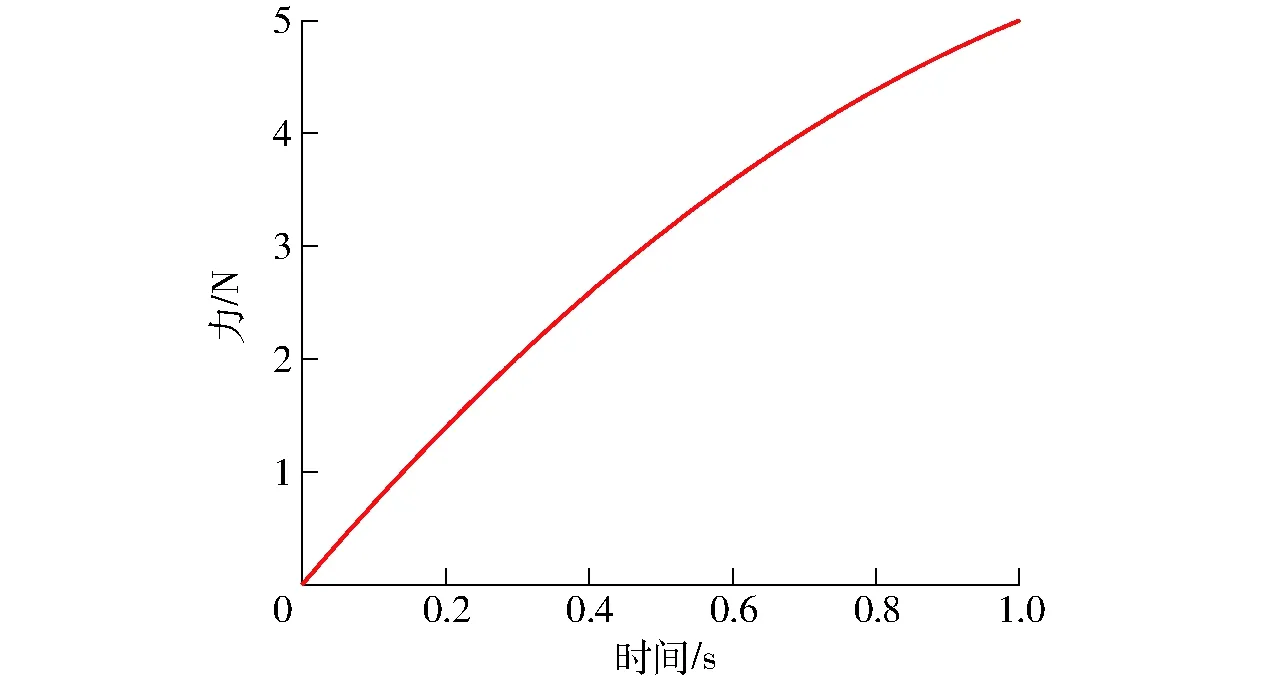
图4 抓取控制方式1的力随时间变化曲线Fig.4 Changing curve of force over time of the first grasping control mode

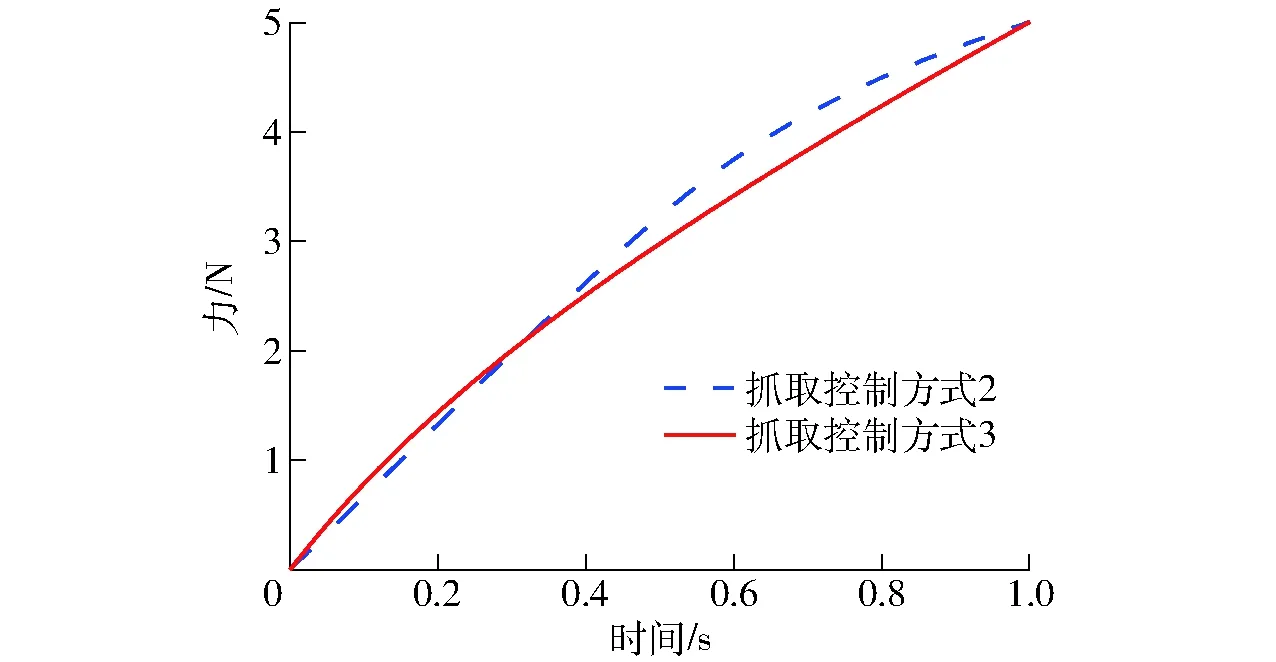
图5 抓取控制方式2和抓取控制方式3的力随时间变化曲线Fig.5 Changing curves of force over time of the second and third grasping control modes

图6 3种抓取控制方式下红熟前期番茄的塑性变形规律Fig.6 Plastic deformations of early maturity tomato with three grasping control modes

图7 3种抓取控制方式下红熟中期番茄的塑性变形规律Fig.7 Plastic deformations of middle maturity tomato with three grasping control modes

通过对比3种典型抓取控制方式，可以得出：在相同抓取速度下，抓取控制方式2产生的塑性变形最大，抓取控制方式3产生的塑性变形最小；当抓取速度v0=20 mm/s，t0=4 s时，抓取控制方式2产生的塑性变形Xp最大，红熟前期和红熟中期番茄的最大塑性变形分别为0.105 mm和0.119 mm；抓取速度v0=1 mm/s，t0=1 s时，抓取控制方式3产生的塑性变形最小，红熟前期和红熟中期番茄的最小塑性变形分别为0.002 6 mm和0.009 8 mm。因此，为了减少作业过程产生的塑性变形，降低番茄的机械损伤，采取合适的抓取控制方式具有重要意义。综上分析，应选择抓取控制方式3为番茄采摘机械手的最优抓取控制方式，即变减速抓取控制策略。

3.3 抓取实验

为验证抓取过程中番茄塑性变形理论分析的正确性，以及选择抓取控制方式3作为造成机械损伤较小的抓取控制方式的合理性和可行性。利用式(8)表征的番茄力-位移关系模型，结合当前实验平台，在抓取速度v0=1 mm/s，抓取时间t0=1 s的抓取条件下，对番茄样本开展抓取实验与理论分析。

实验平台采用德国SCHUNK公司生产的WSG 50型电动二指平行夹指，如图8所示。该末端执行器整合了控制器、编码器和SD存储卡，与PC机的通讯协议为TCP/IP协议。其中一个力反馈手指可以实时测量番茄的接触力，手指的位移由编码器测量。设定机械手的抓取速度v0=1 mm/s，抓取时间t0=1 s，利用该实验平台对上述选择的红熟前期的番茄以抓取控制方式3进行抓取实验，分析其可行性。

图8 抓取实验平台Fig.8 Grasping experimental platform1.信息采集系统 2.WSG 50型机械手 3.力反馈手指 4.稳压电源

图9为以抓取控制方式3完成稳定抓取过程时，番茄的接触力随时间变化的实验数据与理论数据曲线。从图9中可以看出，理论数据和实验数据的吻合度较高，通过Origin 8.0统计分析，确定实验数据和理论数据的决定系数R2=0.99，该模型能较准确地描述抓取过程中番茄的受力特征。由式(13)可知，塑性变形是由抓取过程中接触力变化最终决定，表明了以此为基础进行的番茄塑性变形理论分析的正确性。因此，可选择抓取控制方式3为造成机械损伤较小的抓取控制方式，为优化采摘机械手抓取过程提供依据。

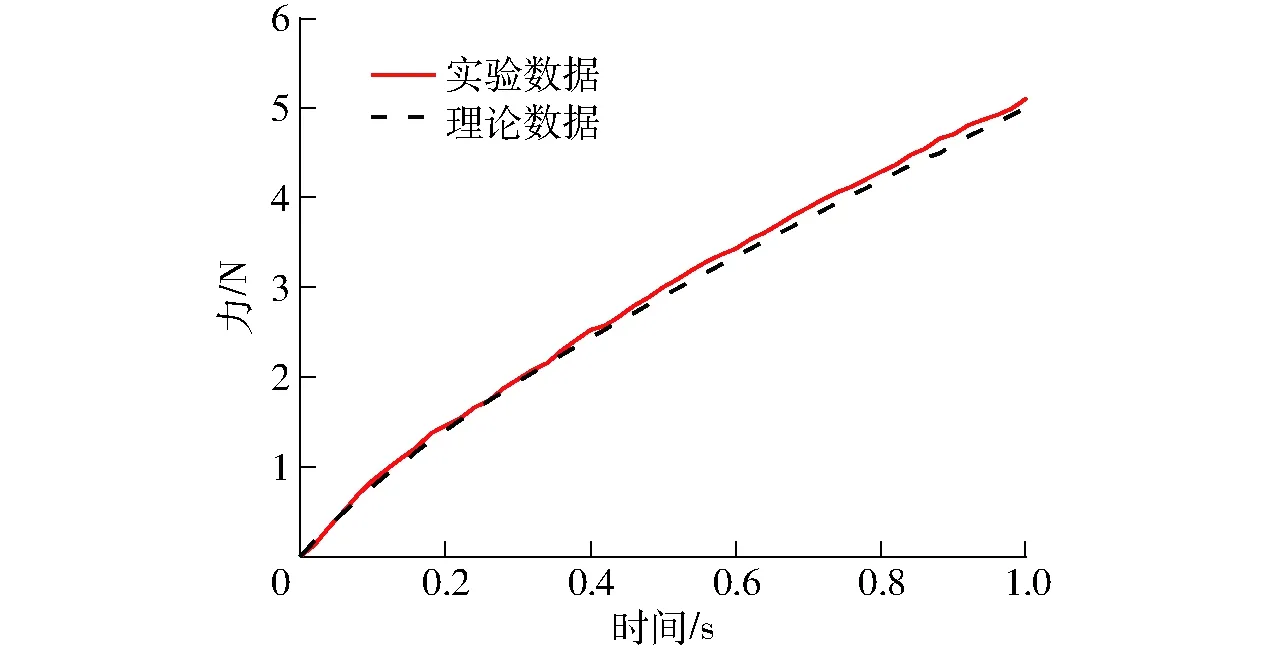
图9 抓取控制方式3的理论与实验曲线Fig.9 Theory and test curves of the third grasping control mode

4 结论

(1)以Burgers模型描述番茄的变形特征，通过Origin 8.0数据分析软件对红熟前期和红熟中期的番茄蠕变曲线进行拟合，得到粘弹性参数k1、k2、c1、c2，且拟合决定系数均在0.992以上。

(2)利用一次函数、巴特沃斯幅度平方函数以及指数函数，分别表征采摘机械手匀减速、先匀速后减速和变减速3种典型的抓取控制方式。以塑性变形作为衡量番茄机械损伤的关键因素，根据理论计算确定最小塑性变形量，选择抓取控制方式3作为最优抓取控制策略。当抓取速度v0=1 mm/s，抓取时间t0=1 s时，产生的塑性变形Xp最小，红熟前期和红熟中期番茄的最小塑性变形分别为0.002 6、0.009 8 mm。

(3)实验与理论数据对比结果表明：实验和理论模型的吻合度较高，决定系数R2为0.99，验证了抓取控制方式3作为抓取策略的可行性和有效性。

1 BELFORTE G, DEBOLI R, GAY P, et al. Robot design and testing for greenhouse applications[J]. Biosystems Engineering, 2006, 95(3): 309-321.

2 方建军. 移动式采摘机器人研究现状与进展[J]. 农业工程学报, 2004, 20(2): 273-278.

FANG Jianjun. Present situation and development of mobile harvesting robot[J]. Transactions of the CSAE, 2004, 20(2): 273-278.(in Chinese)

3 曹海燕, 卢立新. 梨果实跌落冲击特性与流变模型[J]. 食品与生物技术学报, 2007, 26(4):11-15.

CAO Haiyan, LU Lixin. The dropping impact behavior and rheological model of pear[J]. Journal of Food Science and Biotechnology, 2007, 26(4):11-15.(in Chinese)

4 卢立新, 王志伟. 基于准静态压缩的果实黏弹塑性模型[J]. 农业工程学报, 2005, 21(12):30-33.

LU Linxin, WANG Zhiwei. Nonlinear viscoelastic plastic model of the fruits under quasi-static compressive loading[J].Transactions of the CSAE, 2005, 21(12):30-33. (in Chinese)

5 TSAI C H D, KAO I, SHIBATA A, et al. Experimental study of creep response of viscoelastic contact interface under force control[C]∥International Conference on Intelligent Robots and Systems, IEEE, 2010:4275-4280.

6 LI Z G, LIU J Z, LI P P, et al. Study on the collision-mechanical properties of tomatoes gripped by harvesting robot fingers[J]. African Journal of Biotechnology, 2009, 8(24):7000-7007.

7 AHMADI E, BARIKLOO H, KASHFI M. Viscoelastic finite element analysis of the dynamic behavior of apple under impact loading with regard to its different layers[J]. Computers and Electronics in Agriculture, 2016, 121: 1-11.

8 HIGASHIMORI M, YOSHIMOTO K, KANEKO M. Active shaping of an unknown rheological object based on deformation decomposition into elasticity and plasticity[C]∥Robotics and Automation (ICRA), IEEE International Conference on Robotics and Automation, IEEE, 2010: 5120-5126.

9 姬伟, 李俊乐, 杨俊, 等. 机器手采摘苹果抓取损伤机理有限元分析及验证[J]. 农业工程学报, 2015,31(5): 17-22.

JI Wei, LI Junle, YANG Jun, et al. Analysis and validation for mechanical damage of apple by gripper in harvesting robot based on finite element method[J]. Transactions of the CSAE, 2015,31(5): 17-22. (in Chinese)

10 陈燕, 谈建豪, 蒋志林,等. 柑橘机器人夹持损伤有限元预测及试验验证[J]. 华南农业大学学报,2016,37(5):98-102.

CHEN Yan, TAN Jianhao, JIANG Zhilin, et al. Finite element prediction and experimental verification for damage on citrus fruit from robot clamping[J]. Journal of South China Agricultural University, 2016, 37(5):98-102. (in Chinese)

11 刘继展，白欣欣，李萍萍，等. 果实快速夹持复合碰撞模型研究[J/OL]. 农业机械学报,2014, 45(4):49-54. http:∥www.j-csam.org/ch/reader/view_abstract.aspx?file_no=20140408amp;flag=1amp;journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2014.04.008.

LIU Jizhan, BAI Xinxin, LI Pingping, et al.Complex collision model in High-speed gripping of fruit[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2014, 45(4):49-54. (in Chinese)

12 马晓丽, 陈晓英, 闫语丝,等. 杨梅果的机械损伤试验和生物力学特性[J]. 农业工程学报,2012, 28(16):282-287.

MA Xiaoli, CHEN Xiaoying, YAN Yusi, et al. Mechanical damage test and biomechanical characteristics of red bayberry fruit[J].Transactions of the CSAE, 2012, 28(16): 282-287. (in Chinese)

13 熊威，甘忠，许旭东，等. 基于粘弹塑性模型的时效成形仿真[J]. 塑性工程学报, 2012, 19(2): 33-37.

XIONG Wei, GAN Zhong, XU Xudong, et al. Simulation for age forming based on viscoelastic plastic model[J]. Journal of Plasticity Engineering, 2012, 19(2): 33-37. (in Chinese)

14 张亚新，郑晓，林国祥. 葵花籽压榨过程中的塑性模型[J]. 农业机械学报, 2009, 40(7): 138-142.

ZHANG Yaxin, ZHENG Xiao, LIN Guoxiang. Plasticity model for pressing of sunflower seeds[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(7): 138-142. (in Chinese)

15 TUDOR C S N, DANIELA I N, MARIAN V, et al. An experimental method for determining the time of relaxation at static compression of apples[J]. Journal of Engineering Studies amp; Research, 2011, 17(2):18-27.

16 LIU J Z, BAI X X, LI P P. Modified Burger’s model for describing creep behavior of tomato fruits[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(9):249-255.

17 SAKAMOTO N, HIGASHIMORI M, TSUJI T, et al. An optimum design of robotic food handling by using Burger model[J]. Intelligent Service Robotics, 2008, 2(1):53-60.

18 李瀚如, 潘君拯. 农业流变学导论[M]. 北京：农业出版社, 1990.

19 杨玲, 张彩霞, 康国栋,等. 华红苹果果肉的流变特性及其主成分分析[J]. 中国农业科学, 2015, 48(12):2417-2427.

YANG Ling, ZHANG Caixia, KANG Guodong, et al. Rheologic properties of Huahong apple pulp and their principal component analysis[J]. Scientia Agricultura Sinica, 2015, 48(12):2417-2427. (in Chinese)

20 李小昱, 朱俊平, 王为,等. 苹果蠕变特性与静载损伤机理的研究[J]. 西北农林科技大学学报：自然科学版, 1997，25(6):64-68.

LI Xiaoyu, ZHU Junping, WANG Wei, et al. A study on creep properties and static loading damage mechanisms of apple[J]. Journal of Northwest A amp; F University: Natural Science Edition, 1997,25(6):64-68. (in Chinese)

21 杨晓清, 王春光. 河套蜜瓜静载蠕变特性的试验研究[J]. 农业工程学报, 2007, 23(3):202-207.

YANG Xiaoqing, WANG Chunguang. Creep properties of Hetao muskmelon under static loading[J]. Transactions of the CSAE, 2007, 23(3):202-207. (in Chinese)

22 李智国. 番茄采摘机器人夹持系统的加减速过程研究[D]. 镇江：江苏大学, 2009.

LI Zhiguo. Acc/Dec process of the grip system on tomato harvesting robot[D].Zhenjiang: Jiangsu University,2009. (in Chinese)

ImpactofRobotGraspingControlModesonMechanicalDamageofTomato

ZHOU Jun MENG Yimeng ZHANG Na YAN Zhenghong

(KeyLaboratoryofIntelligentAgriculturalEquipmentinJiangsuProvince,NanjingAgriculturalUniversity,Nanjing210031,China)

In order to analyze the impact of robot grasping control modes on mechanical damage of tomato, the Burgers model was used to express the deformation characteristics of tomato, and the viscoelastic parameters of tomato were obtained by the creep experiment. Three kinds of variations of speed, i.e., motion with uniform deceleration, deceleration after uniform motion and motion with variable deceleration were selected to indicate different grasping control modes. The linear function, Butterworth amplitude square function and exponential function were used to represent different grasping control modes during the robot grasping process. On this basis, the model of plastic deformation of tomato was solved, and the rules of tomato plastic deformations in different grasping control modes were analyzed when the grasping time was constant. Then, the optimal grasping strategy was selected based on the minimum plastic deformation. Experimental results indicated that the third grasping control mode was selected as the best grasping strategy, when the grasping speed was 1 mm/s, the grasping time was 1s, the plastic deformation of tomato was the smallest, the early maturity and middle maturity of plastic deformations were 0.002 6 mm and 0.009 8 mm, respectively. Using the third grasping control mode to carry out the grasping control experiment, the simulation results were highly identical with measured results, the determination coefficientR2was 0.99, which proved the rationality and feasibility of the third mode as the optimal grasping control mode. This research can offer a reference for robots grasping process optimization.

tomato; picking; robot; grasping control mode; mechanical damage

10.6041/j.issn.1000-1298.2017.11.003

TP24

A

1000-1298(2017)11-0021-07

2017-03-03

2017-03-23

国家自然科学基金项目(31471419)和教育部博士点基金博导类项目(20130097110043)

周俊(1974—)，男，教授，博士生导师，主要从事农业机器人和机器视觉与模式识别研究，E-mail： zhoujun@njau.edu.cn