存在部分连通断层的条带状油藏试井解释新模型

曾 杨， 康晓东， 谢晓庆， 石 爻， 张烈辉

(1.海洋石油高效开发国家重点实验室， 北京 100028； 2.中海油研究总院， 北京 100028； 3.西南石油大学 油气藏地质及开发工程国家重点实验室， 四川 成都 610500)

存在部分连通断层的条带状油藏试井解释新模型

曾 杨1,2， 康晓东1,2， 谢晓庆1,2， 石 爻1,2， 张烈辉3

(1.海洋石油高效开发国家重点实验室， 北京 100028； 2.中海油研究总院， 北京 100028； 3.西南石油大学 油气藏地质及开发工程国家重点实验室， 四川 成都 610500)

条带状油藏是断块油田中最常见的构造形态之一，国内外学者对非封闭断层的研究大都集中于均质油藏和复合油藏.因此，用现有的试井解释模型对具有存在非封闭断层的条带状油藏试井资料进行解释所得到的结果往往并不理想.通过引入界面表皮的概念，将部分连通断层视为一个无限薄的表皮边界，建立了条带状油藏中存在部分连通断层的试井解释新模型，并利用Fourier指数变换和Laplace变换等方法进行求解，绘制了井底压力响应特征曲线.分析表明：界面表皮越大，曲线上翘越多，当它足够大时，表现为封闭断层的特征；边界距离对典型曲线形态的影响显著；流度比、厚度比、导压系数比主要影响压力导数曲线上升和下降.

部分连通断层； 条带状油藏； 界面表皮； 试井模型； 典型曲线

0 引言

国内外学者对封闭断层[1-4]的研究较为系统和成熟.一般的，常用于判别封闭断层的方法就是Horner半对数曲线法[5].1975年，Prasad和Tiab等[6-8]将存在一条封闭断层边界的模型扩展到多条交叉或者平行的封闭断层模型.然而，目前对非封闭断层的研究大都集中于均质油藏和复合油藏.Bixel等[9]首次提出将断层视为非封闭边界，但他所建立模型仅仅考虑岩石和流体性质在平面上发生突然变化的情形，Kuchuk等[10]后来对该模型的求解方法进行了完善.1984年，Stewart和Streltsova等[11，12]在Bixel研究的基础上通过数值模拟研究了部分连通断层对干扰试井的影响.Yaxely[13]、李传亮[14]推导了无限大均质油藏中含有部分连通断层模型的解析解.在此基础上，Ambastha和张望明等[15，16]进一步研究了复合油藏中存在部分连通断层边界的井底压力响应特征.

上述对条带状油藏中存在非封闭断层的情况并没有研究，而实际油藏由于沉积环境的影响，断块油田中最常见的构造形态之一为条带状油藏，它直接影响到后续压力波传播到断层边界的反应.

为此，本文通过引入Everdingeen[17]和Hurst[18]提出的界面表皮的概念，将部分连通断层视为一个无限薄的表皮边界，建立了存在部分连通断层的条带状油藏试井解释新模型，绘制了模型的井底压力响应特征曲线并对相关的影响因素进行了分析.

1 渗流物理模型

针对两条平行不渗透边界的条带状油藏中存在部分连通断层的情形，如图1所示.假设断层两侧的岩石特性、储层厚度及渗透率不同，但同一区域内为均质油藏且各向同性.激动井为定产量线源，且流体为微可压缩等温渗流，流动服从达西定律.引入界面表皮的概念考虑两个储层区域之间断面的传导率，忽略重力和毛管力的影响.

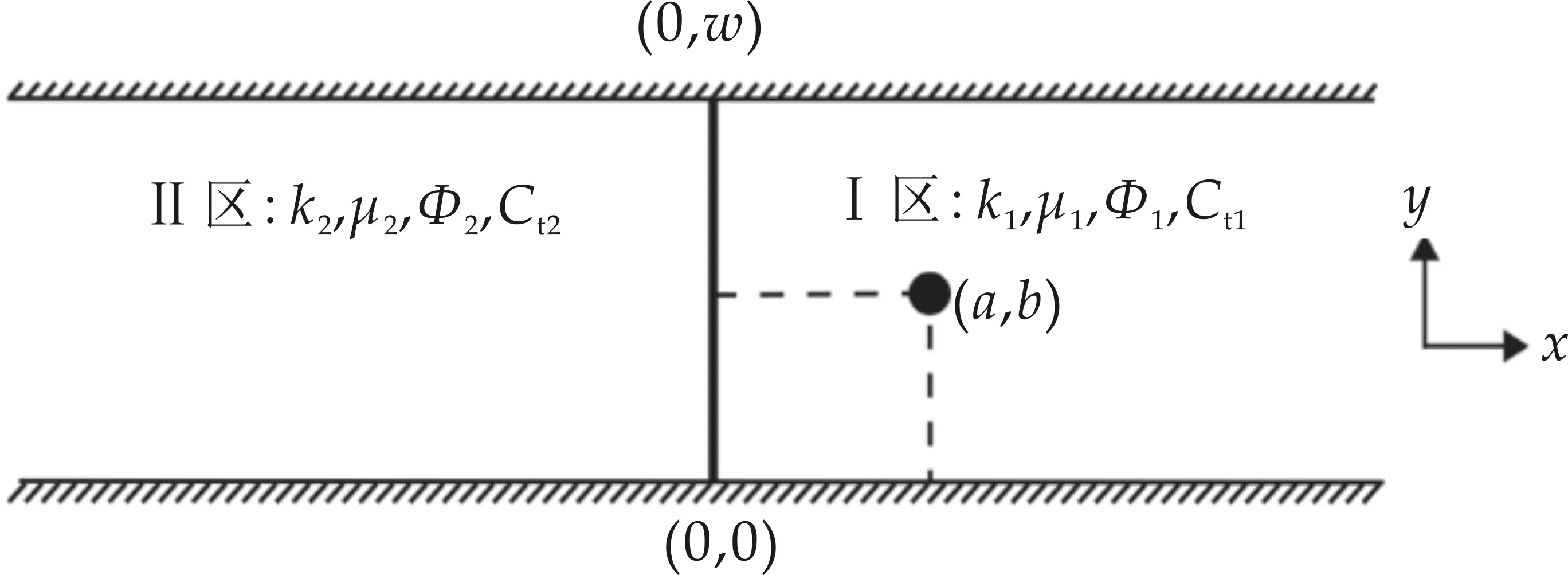
图1 存在部分连通断层的条带状油藏示意图

2 数学模型的建立及求解

2.1 数学模型的建立

根据图1所建立的坐标系和上述假设条件，以基本的渗流力学理论为依据，根据前面的假设条件，激动井为定产量线源，且以产量q生产，开井前地层各处压力相等，均为pi，根据点源函数理论，可推导出条带状油藏中存在部分连通断层的无因次试井解释模型.

(1)渗流微分方程

Ⅰ区，对xDgt;0：

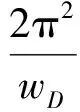
(1)

Ⅱ区，对xDlt;0：

(2)

式(1)～(2)中，无因次变量分别为：

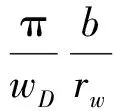
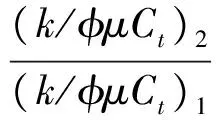
其中：p1D、p2D-Ⅰ区、Ⅱ区的无因次压力；wD、xD、yD、aD、bD-无因次距离；tD-无因次时间；M-流度比；hD-厚度比；ηD-导压系数比；p1、p2-Ⅰ区、Ⅱ区压力；k1、k2-Ⅰ区、Ⅱ区地层渗透率；h1、h2-Ⅰ区、Ⅱ区地层厚度；μ1、μ2-Ⅰ区、Ⅱ区流体粘度；φ1、φ2-Ⅰ区、Ⅱ区孔隙度；Ci1、Ci2-Ⅰ区、Ⅱ区地层综合压缩系数；x、y-横、纵坐标；a、b-井点横、纵坐标；δ-δ函数表示定产量线源井.

(2)初始条件

p1D(xD,yD,0)=p2D(xD,yD,0)=0

(3)

(3)边界条件

x方向的边界条件：

p1D(∞D,yD,tD)=p2D(∞D,yD,tD)=0

(4)

y方向的边界条件：

(5)

(4)连接条件

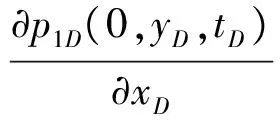
(6)

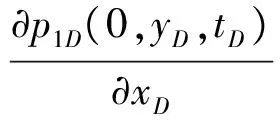
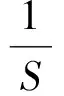
(7)

2.2 数学模型的求解

对上述无因次试井模型式(1)～(7)取基于yD的Fourier指数变换和基于tD的Laplace变换并化简，可得：

(8)

式(8)中：

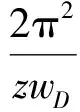
求解可得：

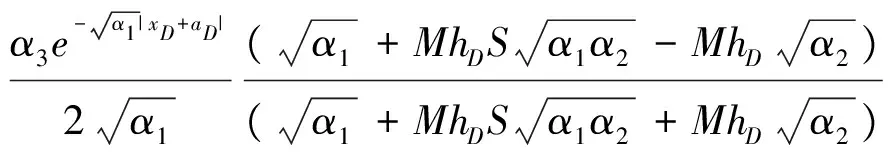
xDgt;0

(9)

xDlt;0

(10)

要求生产井的井底压力，令xD=aD-1，yD=bD，得：

xDgt;0

(11)

3 典型曲线的绘制及特征分析

3.1 边界距离的影响

图2所示为井位于条带状地层中部(bD/wD=0.5)，aD、bD对典型曲线的影响.从图2可以看出，无论aD、bD取值如何，典型曲线早期都表现出井储阶段的特征，压力与压力导数曲线重合，二者均为斜率为1的直线.随着压力波的不断向外传播，当tD较小时，压力波尚未传播到任何断层边界或界面，地层中表现出均质储层渗流特征，压力导数曲线表现为0.5水平线，该阶段持续时间的长短取决于aD和bD中的较小值.

当aD/bDlt;1时，如图2中的aD/wD=0.05情况，随着tD不断增大，压力波首先传播到两区分界面处，由于此时考虑分界面的界面表皮S=106，这已接近于封闭断层，因此压力导数曲线上翘并出现第二个水平段，该水平段值趋于1，反映出分界面处为封闭断层的特征，曲线上翘值的大小取决于界面表皮S值的大小，S越大，上翘越多，并最终趋于封闭断层的特征.该水平段在压力波传播到平行断层边界时结束，其持续时间取决于井到平行断层边界的距离bD.由于井位于条带状地层中部(bD/wD=0.5)，故压力波同时传到两平行断层边界处，之后地层中流动变为等效均质储层中的线性流，压力导数曲线表现为斜率为1/2的直线.

当aD/bD=1时，如图2中的aD/wD=0.5情况，经过早期井储流动和Ⅰ区均质储层径向流阶段后，压力波同时传到两平行断层边界和区域交界面处.由于交界面处S=106，已接近与封闭断层，此时会出现一短暂的过渡阶段，过渡段结束后，地层中流动进入等效均质储层线性流阶段，压力导数曲线表现为斜率为1/2的直线.

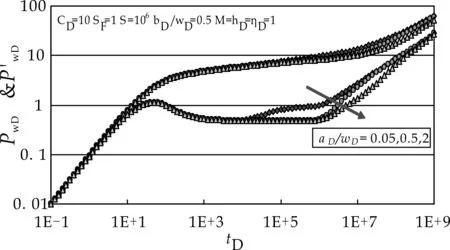
图2 aD和bD对典型曲线的影响(井位 于条带状地层中部)

当aD/bDgt;1时，如图2中的aD/wD=2情况，经过早期井储流动和Ⅰ区均质储层径向流阶段后，随着tD不断增大，压力波首先传播到平行断层边界，地层中出现均质储层线性流，压力导数曲线表现为斜率1/2的直线，该阶段一直持续到压力波传播到区域界面aD处为止.当压力波继续向外传播至两区界面时，由于界面处S=106，此时典型曲线上会出现短暂的过渡段，过渡段结束后，地层中流动进入等效均质储层线性流阶段，压力导数曲线又出现斜率为1/2的直线.需要注意的是，第二次出现的1/2斜率直线段反映的是等效均质储层中的线性流，故与之前出现的1/2斜率直线段并不重合，两直线截距之差的大小与S值、流度比和导压系数比等相关.

3.2 界面表皮S的影响

图3显示了当井靠近条带状地层的一条断层边界时，界面表皮S对井底压力动态曲线的影响.由于aD/bDlt;1，压力波首先传到两区分界面，界面表皮S主要影响压力导数曲线上第二个水平段位置的高低，S越大，说明Ⅰ区与Ⅱ区的连通性越弱，流体在地层中流动的压力损失就越大，压力导数曲线由0.5水平线开始上翘，随着S值的不断增大，上翘越多.当S=106时，两区分界面趋于封闭断层，压力导数曲线表现出值为1的水平线，随后，当压力波继续传到其中一条断层时，此时形成角度为90 °的夹角断层，压力导数曲线表现出值为2的水平线，最后出现的反映等效均质储层线性流的1/2斜率压力导数曲线.当S=103时，两区分界面部分连通，当压力传播到此分界面，由于界面表皮的存在，流体流动的压力损失增大，压力导数曲线逐渐从0.5水平线开始上翘，随着Ⅱ区流体开始流动压力有所下降，随后，当压力波继续传到其中一条断层时，流动阻力再一次增加，压力导数曲线出现上翘，直到压力波传播到另外一条断层边界，最后出现反映等效均质储层线性流的1/2斜率压力导数曲线.

图3 界面表皮对典型曲线 的影响(aD/bDlt;1)

3.3 流度比、厚度比、导压系数比的影响

图4显示了流度比M对井底压力动态曲线的影响.当aD/bDlt;1时，流度比M主要影响压力导数曲线上第二个水平段位置的高低，M越大，说明Ⅱ区物性越好，流体在地层中流动的压力损失就越小，压力导数曲线就下降越多，最后出现的反映等效均质储层线性流的1/2斜率压力导数曲线位置也越靠下.

厚度比hD与导压系数比ηD对井底压力动态的影响与流度比M对井底压力动态的影响类似，这里就不在一一赘述.

图4 流度比对典型曲线 的影响(aD/bDlt;1)

4 结论

(1)条带状油藏边界直接影响到后续压力波传播到断层后的反应，首次建立了条带状油藏中存在部分连通断层边界的试井解释新模型，对具有类似边界条件的油藏研究和应用具有一定的借鉴意义.

(2)边界距离对存在部分连通断层条带状油藏典型曲线形态的影响显著；当界面表皮S值足够大时，表现为封闭断层的特征；流度比主要影响压力波传到Ⅱ区之后的压力动态，流度比越大，压力及压力导数曲线的位置越靠下，厚度比与导压系数比对井底压力动态的影响与流度比类似.

(3)本文提出的断层模型可用于双重介质油藏、复合油藏等的试井解释及压力分布规律研究.

[1] 王 奎，杨 静，侯光宗，等.断层封闭性研究现状及其发展趋势[J].断块油气田，2008，15(3)：43-45.

[2] 周 路，王丽君，罗晓容，等.断层连通概率计算及其应用[J].西南石油大学学报(自然科学版)，2010，32(3)：11-18.

[3] 叶双江，姜汉桥，孙传宗，等.断块油藏水平井产能研究及断层封堵影响分析[J].西南石油大学学报(自然科学版)，2011，33(5)：131-136.

[4] 张 旭，刘启国，张小龙，等.断层板状油藏斜井试井模型研究[J].天然气与石油，2012，30(5)：60-63.

[5] Horner D R.Pressure build-up in wells[C]//Presented at the 3rd World Petroleum Congress.Hague：SPE,1951：503-521.

[6] Prasad R K.Pressure transient analysis in the presence of two intersecting boundaries[J].JPT,1975,27(1)：89-96.

[7] Tiab D,Kumar A.Detection and location of two parallel sealing faults around a well[J].JPT,1980,32(10)：1 701-1 708.

[8] Earlougher R C.Pressure distributions in a rectangular reservoirs[J].JPT,1968,20(2)：199-208.

[9] Bixel H C,Larkin B K,Van Poolen H K.Effect of linear discontinuity on pressure buildup and drawdown behavior[J].JPT,1963,15(8)：885-895.

[10] Kuchuk F J,Habashy T M.Pressure behavior of laterally composite reservoir[J].SPEFE,1997,12(1)：47-56.

[11] Stewart G,Gupta A,Westaway P.The interpretation of interference tests in a reservoir with a sealing and a partially communicating faults[C]//Presented at the 1984 European PetroIeum Conference.London：SPE,1984：411-429.

[12] Streltsova T D,McKinley R M.Effect of flow time duration on buildup pattern for reservoirs with heterogeneous properties[J].SPEJ,1984,24(3)：294-306.

[13] Yaxely L M.Effect of partially communicating fault on transient pressure behavior[J].SPEFE,1987,2(4)：590-598.

[14] 李传亮.非封闭断层的试井解释方法[J].新疆石油地质，1997，18(4)：370-376.

[15] Ambastha A K,McLeroy P G,Grader AS.Effect of a partially communicating fault in a composite reservoir on transient pressure testing[J].SPEFE,1989,4(2)：210-218.

[16] 张望明，曾 萍.存在局部连通断层的复合油藏不稳定试井分析及典型曲线拟合方法[J].石油勘探与开发，1992，19(2)：69-76.

[17] Van Everdingen A F.The skin effect and its influence on the productivity capacity of a well[J].JPT,1953,5(6)：171-176.

[18] Hurst W.Establishment of the skin effect and its impediment to fluid flow in a wellbore[J].Pet.Eng,1953,25(8)：6-16.

【责任编辑：蒋亚儒】

Transientpressurebehavioranalysisinabandedreservoirwithpartiallycommunicatingfaults

ZENG Yang1,2， KANG Xiao-dong1,2， XIE Xiao-qing1,2， SHI Yao1,2， ZHANG Lie-hui3

(1.State Key Laboratory of Offshore Oil Exploitation, Beijing 100028, China； 2.CNOOC Research Institute, Beijing 100028, China； 3.State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation， Southwest Petroleum University， Chengdu 610500, China)

Banded reservoir is one of the most common structures in fault block reservoir,most of the researches on non-closed faults are concentrated in homogeneous reservoirs and composite reservoirs.When we used the existing well testing interpretation models to interpret the actual banded reservoir well test data with partially communicating fault boundary,the obtained results are not always ideal.A well testing model for wells located near a partially communicating fault in a two-zone,banded reservoir was established by introduced the “boundary skin” concept,the solution was obtained with the Fourier and Laplace transformation.Type curves were plotted by the Stehfest numerical inversion method and this model was verified by the examples.The result showed that the bigger the boundary skin value,the more the curve upturned;the boundary distance has a significant effect on the typical curve shape;the mobility ratio,thickness ratio,pressure conductivity coefficient mainly affected the pressure derivative curve rise and fall..

partially communicating fault； banded reservoir； boundary skin； well testing model； type curve

2017-08-03

国家科技重大专项项目(2016ZX05025-003)； 中海石油有限公司综合科研项目(YXKY-2014-ZY-03)

曾 杨(1987-)，女，四川广安人，工程师，硕士，研究方向：油气田开发及提高采收率

2096-398X(2017)06-0104-05

TE353

A