基于“共享单车”问题的矩阵分析

田献珍++靳宝霞

摘要：本文主要根据《2017年MathorCup大学生数学建模挑战赛B题》附件1中的数据，利用MATLAB软件对采集的数据进行了处理，并利用矩阵的乘法运算及矩阵特征值与特征向量对共享单车问题进行分析。

Abstract： In this paper， mainly based on the data of"2017 MathorCup College Students Mathematical Modeling Challenge B，" Annex 1， MATLAB software is used to deal with the collected data and matrix multiplication and matrix eigenvalues and eigenvectors are used to analyze the sharing-bikes problem.

关键词：系数矩阵；矩阵的乘法运算；矩阵的特征值和特征向量

Key words： coefficient matrix；matrix multiplication；matrix eigenvalues and eigenvectors

中图分类号：U492.2+2 文献标识码：A 文章编号：1006-4311（2017）36-0011-02

0 引言

共享单车以分时租赁模式，为校园、地铁站点、公交站点、居民区、商业区等公共服务区提供自行车共享服务，已经越来越多地引起人们的注意。

很多共享单车公司的单车都有GPS定位，能够实现动态化地监测车辆数据、骑行分布数据，进而对单车做出全天候供需预测，为车辆投放、调度提供指引。

本文主要根据《2017年MathorCup大学生数学建模挑战赛B题》附件1中的数据，给出矩阵的乘法运算及矩阵特征值与特征向量在共享单车问题中的应用。

1 原始数据分析

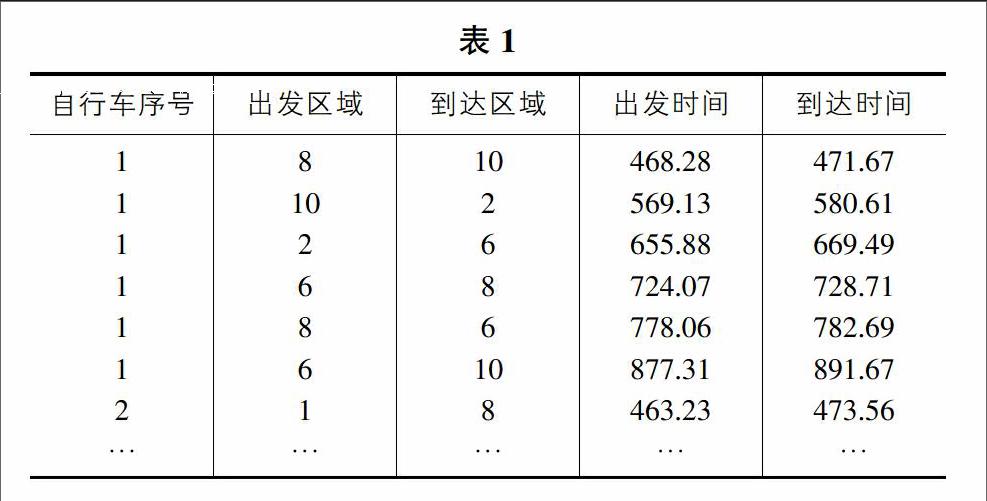
附件1中部分数据如表1所示。

所采集的数据信息时间段为6：00到24：00。假设企业的调度时间段为24：00到6：00之前。容易统计出各区全天最大的需求量为：

zdxq=[39 50 22 34 40 34 25 49 30 24]，

由于各区自行车是相互流动的，那么只要每天在6：00之前向各区投放如向量zdxq所示的車辆时，各区全天的骑行需求得到满足。

假设各区早上投放车辆为向量zdxq，再统计各区24：00为止停放的车辆数为

zz=[41 41 21 26 52 37 33 33 36 27]，

那么，每天24：00后需要调度的车辆数为：

dd=[2 -9 -1 -8 12 3 8 -16 6 3]

其中6个区域比6：00之前多出34辆车，4个区域比6：00之前少了34辆车，总的调度车辆数为34辆。endprint