基于Elman神经网络算法的电力负荷预测模型研究

李 文

（安徽机电职业技术学院，安徽 芜湖 241000）

基于Elman神经网络算法的电力负荷预测模型研究

李 文

（安徽机电职业技术学院，安徽 芜湖 241000）

随着社会经济的发展，也为电力负荷系统带来极大的考验.如何才能够让电力保持平稳、高质量的输送，使客户的用电需求得到用力保证，避免因为断电给客户造成极大的经济损失，这我们需要不断思索的问题.随着依托于人工神经系统的新预测技术出现，对电力负荷的预测越来越准确，在保障电力顺利平稳输送的同时，也减少可人工成本的支出.本文通过Elman型神经网络，对电力负荷预测进行研究，并通过Matlab进行仿真.

神经网络；电力负荷；仿真

前馈型网络是构成神经网络的主要类型之一，另外一种非常重要构成类型则是反馈型网络，这主要是根据信号在神经网络中的走向来看区分的.相比而言，前者是所有神经网络中最早被提出的，也是公认的最简单的一种神经网络，它的工作原理是神经元信号从输入层开始，只能不停地向前流动，一直到输出层为止，如同我们交通道路中的不能掉头的单行道一般.我们通常讲的回归网络，其实就是说反馈型神经网络，这种网络算法比前馈神经网络更为繁杂难算，换而言之，发聩神经网络型就是指神经元信号在从输入层到输出层输送的过程中，可以进行反向输送.因为发聩型神经网络具有十分明显的延迟、发聩等的特征.

这就相当于生活中人们最常用的Elman神经网络，还有Boltzmann神经网络也都算于反馈型神经网络.其中Elman神经网络最有代表性，是Elman在1990年时率先提出的.

1 Elman神经网络结构

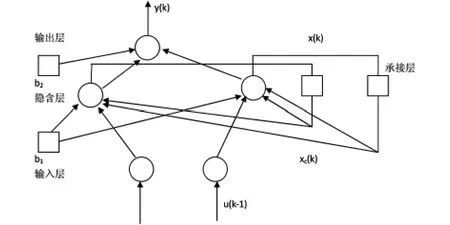
首先是输入这个层面，其次是隐含，还有承接和输出，共同组成了Elman型神经网络的最主要流程.如图23-1示，如果将其中输入、隐含以及输出这三个层次进行相连的话，就会形成一种前馈式网络.

输入层的功能就是对信号进行输送，而输出层的功能就是对信号进行线性加权.隐含层的功能就是进行线性或者非线性函数的传送，可以认为是一个一步延时算子，起到一个承上启下的作用，它主要是对隐含层的传输的信号进行记录以后，并将其传输给输入层.

Elman神经网络有两大突出优势：第一，利用承接层的延迟以及存储排除隐匿层,其可以自动连接到隐含层的进入.上述自动连接的突进能够将过去状态的数据非常灵活,再加上融入了内部反馈网络能够将网络自身处理信息的能力提升,最终建立动态数字模型.第二,它可以任何一个精确度接近任何一个非线性映射,忽视外部噪声对系统的影响,进而建立数字模型.

2 Elman神经网络学习过程

下面就是23_1,Elman网络的非线性状态空间数学计算方式：

y(k)=g(w3x(k))

x(k)=f(w1xc(k)+w2(u(k-1)))

xc(k)=x(k-1)

式中,y为m维输结点向量；x为n维中间层结点单元向量；u维r维输入向量；x为n维反馈状态向量；w3为中间层到输出层连接权值；w2为输入层到中间层连接权值;w1为承接层到中间层连接权值；上式当中，g(*)则代表的是排出神经元传导这个函数，即线性组合用的中间层;f(*)则代表了传导中间层神经元这个函数，我们还会用S来替代.

与此同时，Elman神线网络也使用BP算法.式中，yk（w）为目标输入向量.

3 电力负荷预测机述

发电系统、电网以及用电客户三者统一构成了整个电力系统，不间断地满足广大客户的生产、生活用电需求是电力系统的主要职能.由于电是一种无色无形的能量，具有极大的危险性，再加上存储技术上的限制，电在生产过程的中，很难被大量储存下来.同时，客户对电能的消耗也不是一成不变的，而是随机性发生变化，忽高忽低，这对电力负荷系统带来极大的考验.如何才能够让电力保持平稳、高质量的输送，使客户的用电需求得到用力保证，避免因为断电给客户造成极大的经济损失，这是电力部门正不断思索的问题.随着依托于人工神经系统的新预测技术出现，对电力负荷的预测越来越准确，在保障电力顺利平稳输送的同时，也减少可人工成本的支出.

与传统的预测方法有所不同的是，新的负荷预测方法是运用人工神经网络中的一种非数学模型预测法而建立起来的.而传统的负荷预测方法，先将以往的负荷数据进行人工统计，然后利用数学方程式，建立一个数学模型，其特点就是计算速度十分快，这种预测方法十分适用于对小范围内的电力负荷进行预测.但随着我国社会日新月异，生产、生活用电量与日俱增，在更多的电力系统建设的同时，其电力负荷变化更是越来越复杂.因为传统的预测方法自身也存在着严重的不足，预测范围小，对环境的变化十分不适应，已经满足不了电力部门逐渐增加的需求，因此对新的预测技术进行开发进行改进，成为一个摆在电路部门面前，不得不解决的一个大难题.因为负荷会随着时间的变化而不时发生变化，很难用数学模型来表现清楚，随着一种建立人工神经网络基础上的非数学模型预测法,推动了新的负荷预测方法的出现.

与传统的预测方法有所不同的是，新的预测方法是利用人工神经网络中的一种非数学模型预测法而进行建立的.而传统的负荷预测方法，先将以往的负荷数据进行人工统计，然后利用数学方程式，建立一个数学模型，其特点就是计算速度十分快，这种预测方法十分适用于对小范围内的电力负荷进行预测.但随着我国社会日新月异，生产因为传统的预测方法自身也存在着严重的不足，预测范围小，对环境的变化十分不适应，已经满足不了电力部门逐渐增加的需求，因此对新的的预测技术进行开发进行改进，成为一个摆在电路部门面前，不得不解决的一个大难题.因为负荷会随着时间的变化而不时发生变化，很难用数学模型来表现清楚，随着一种建立人工神经网络基础上的非数学模型预测法的出现,推动了新的负荷预测方法的出现.

4 数学模型建立

随着社会经济的发展，我国的生活、生产用电将人工神经网络和预测方法有机结合起来，并运用二者的突出优势，打造一个数据模型.在所有的人工神经网络中，只有输入延迟的反馈式神经网络,非常适用于网络模型的建立.在网络模型建立后，通过对以往的电力负荷数据和预测数据进行全面比较分析,对电力系统负荷运行的规律进行探索，并对未来的某个时段的电力负荷情况进行预测，为该时段的电力负荷管控提供依据.

通常来讲,每天的9点到19点，是电力系统当天负荷高峰时期.下表是对每天9点到19点电力负荷数据的统计，作者将用这些数据进行一个网络预测，看预测的结果是否和实际数据相一致.

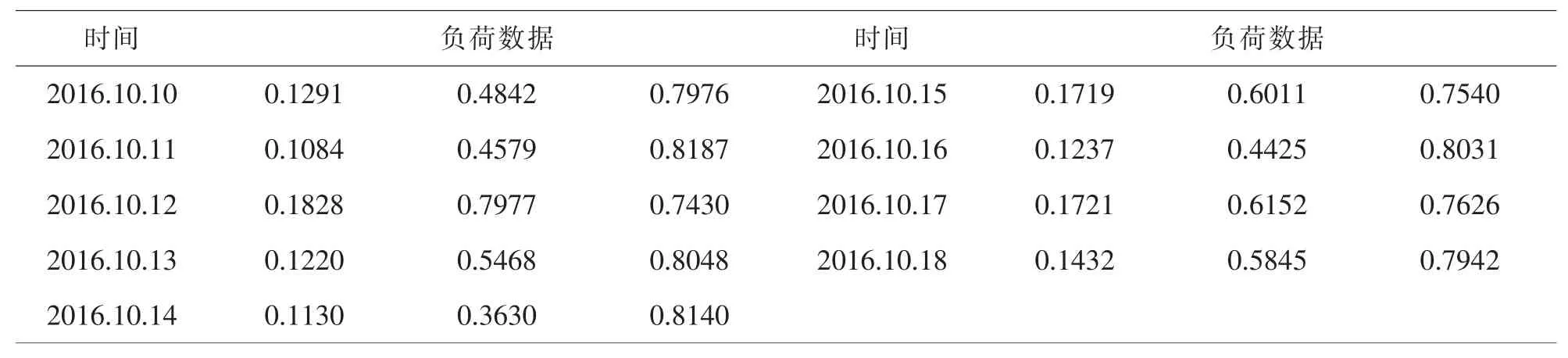
表1 电力系统负荷数据表

5 Matal实现

本例中用到的关键函数为newelm（），其作用为创建一个Elman网络，其调用格式如下：

net=newelm(PR,[S1 S2SN1]，{TF1 TF2TFN1},BTF,BLF,PF,IPF,OPF)

在上述公式中，R版块中要素的具体值是P；T为SN*Q2的具有SN个元素的输出矩阵；Si为第i层的长度；Tfi为第i层的传递函数，默认值：隐藏层为’tansig’，输出层为’purelin’；BTF具体指神经网络反向传达，通常用’trainlm’来表示；BLF具体指神经网络权值指反向传达，一般表示为’learngdm’；PF 为性能函数，默认值为’mse’；IPF 为输入处理函数，默认值为：’{’fixunknowns’,’removeconstantrows’,’mapminmax’}’；OPF 为输出处理函数，默认值为’{ ‘removeconstantrows’,’mapminmax’}’

MATLAB实现代码如下：

% 建立在,Elman神经网络基础上的电力负荷预测模型研究

%% 清空环境变量

clc;

clear all

close all

nntwarn off;

%% 数据载入

load data;

a=data;

%% 选取训练数据和测试数据

for i=1:6

p(i,:)=[a(i,:),a(i+1,:),a(i+2,:)];

end

% 训练数据输入

p_train=p(1:5,:);

% 训练数据输出

t_train=a(4:8,:);

% 测试数据输入

p_test=p(6,:);

% 测试数据输出

t_test=a(9,:);

% 为适应网络结构做转置

p_train=p_train';

t_train=t_train';

p_test=p_test';

%% 网络的建立和训练

% 采用轮回使用，将各个隐藏层神经元的数量进行建立

nn=[7 11 14 18];

for i=1:4

threshold=[0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1];% 进行Elman神经网的构建看不到的层是nn(i)个神经元

net=newelm(threshold,[nn(i),3],{'tansig','purelin'});

% 设置网络训练参数

net.trainparam.epochs=1000;

net.trainparam.show=20;

% 初始化网络

net=init(net);

% Elman网络训练

net=train(net,p_train,t_train);

% 预测数据

y=sim(net,p_test);

% 计算误差

error(i,:)=y'-t_test;

end

%%；利用作图的方式查看具体隐藏层神经元的数量，得到的网络的预料结果

plot(1:1:3,error(1,:),'-ro','linewidth',2);

hold on;

plot(1:1:3,error(2,:),'b:x','linewidth',2);

hold on;

plot(1:1:3,error(3,:),'k-.s','linewidth',2);

hold on;

plot(1:1:3,error(4,:),'c--d','linewidth',2);

title('Elman预测误差图')

set(gca,'Xtick',[1:3])

legend('7','11','14','18','location','best')

xlabel('时间点')

ylabel('误差')

hold off;

预测结果如下图所示：

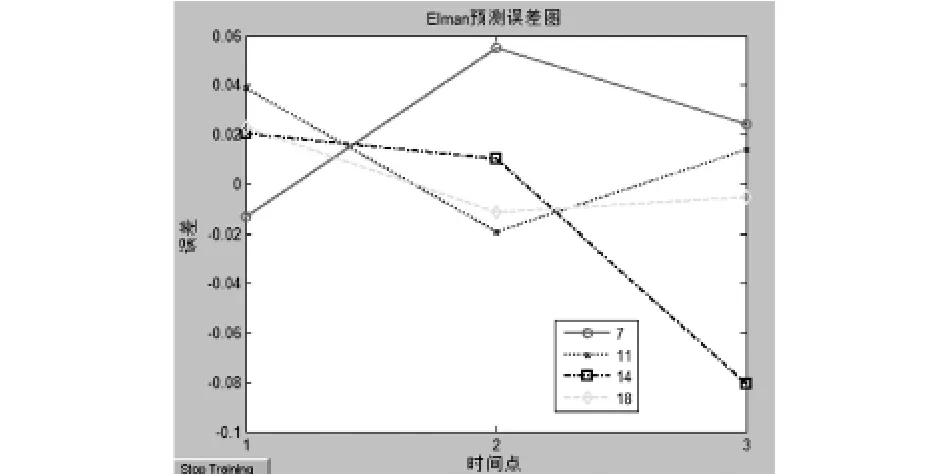
我们可以从上图看出，在这次预测的误差是非常小的，简直可以忽略不计.只有出现7个神经元的时候，存在着较大的误差，这可能和操作不当有关.在出现18个神经元时，误差变成了最小，其波动幅度十分的小，可见18个神经元才是本次负荷预测中最准确的.

其实现在能够准确对电力负荷进行预测的技术其实有很多，每一种的正确率都很高.但是随着电力行业迅速发展，其系统更加庞杂，如何让电力负荷预测能够跟上电力行业的发展步伐，仍需要电力部门进行探索研究.本案例为时间序列类型数据预测提供了依据和思路.但是建立一个电力负荷预测，只有以往的预测数据是远远不够的，毕竟历史不能代表现在，这需要对各个方面进行综合考虑，如电力基础数据、天气情况，工作日和节假日的不同用电量等等.本例由于篇幅有限，对预测模型做了简单化处理，但这并不影响Elman预测功能的演示.

〔1〕邰晓红,王丽娜.基于模糊控制修正Elman神经网络的电力负荷短期动态预测[J].世界科技研究与发展，2016(04）.

〔2〕陈冬沣,肖建华,马留洋,孟安波.基于纵横交叉算法与Elman神经网络的短期负荷预测研究 [J].贵州电力技术，2016(11).

〔3〕郭姣姣.基于改进Elman神经网络的短期电力负荷预测[D].辽宁工业大学.

〔4〕赵铭扬,陈亚,李萍.改进的Elman神经网络在短期电力负荷预测中的应用[J].宁夏工程技术，2016(06).

TP183；TM715

A

1673-260X（2017）11-0038-03

2017-08-07

安徽高校自然科学研究重点项目（KJ2016A141）