基于多孔非稳定抽水试验的缓倾层状含水层各向异性渗透参数计算

江 冰, 唐一格, 夏 强, 许 模

(1.地质灾害防治与地质环境保护国家重点实验室(成都理工大学), 成都 610059；2.重庆诚德岩土工程勘察有限公司,重庆 401147)

基于多孔非稳定抽水试验的缓倾层状含水层各向异性渗透参数计算

江 冰1,2, 唐一格1, 夏 强1, 许 模1

(1.地质灾害防治与地质环境保护国家重点实验室(成都理工大学), 成都 610059；2.重庆诚德岩土工程勘察有限公司,重庆 401147)

探讨通过多孔抽水试验的降深(s)-时间(t)关系获取水文地质参数中的各向异性参数。利用重庆市渝北区某场地砂岩含水层的多孔非稳定流抽水试验数据，结合非轴向各向异性渗透系数张量的理论，通过运用Matlab编程迭代计算了渗透系数张量的比值及其主要方向。结果显示，2组试验结果所获得的数据较为吻合，渗透系数(K)张量的方向θ值范围为[8°, 18°]，Ky/Kx的取值范围为[7.5, 13]。该结果证明了计算方法的适用性和合理性，运用该方法确定含水层各向异性渗透参数所需的核心参数为s-lnt直线在零降深上的截距。

抽水试验；层状含水层；各向异性；渗透系数张量

自20世纪60年代以来，通过抽水试验来确定各向异性岩层渗透张量的研究在国外已有了一定的成果。I.S.Papadopulos[1]最先提出各向异性含水层中的井流公式；随后M.S.Hantush[2]通过坐标变换的方法将各向同性非稳定井流公式转变为各向异性条件下的井流公式。S.Way[3]则提出三维各向异性的渗透系数的确定方法。S.P.Neuman[4]则提出通过三孔两次抽水的确定平面渗透张量的方法。在国内，田开铭等[5]通过对裂隙岩体渗透性的学习并归纳总结，整合编著出版《各向异性裂隙介质渗透性的研究与评价》。周志芳等则于1997年提出通过抽水试验确定渗透系数张量的半解析法[6]，并于2015年通过单孔微水振荡试验现场确定裂隙导水系数及岩体渗透系数张量[7]。相对国外的研究进展，中国学者对渗透系数张量的研究多着眼于岩体裂隙特征，许模等[8]通过对岩体裂隙发育特征的研究确定岩体的各向异性渗透张量；刘青泉等[9]则通过引入裂隙的贯通系数概念，结合随机裂隙网络生成技术，得出估算等效二维裂隙等效渗透系数张量的叠加算法；而关于抽水试验确定岩体各向异性参数的研究仍然较为缺乏。

本文通过非稳定抽水试验所得降深值，结合非轴向各向异性渗透系数张量的理论确定方法，直接计算出目标含水层各向异性渗透系数张量比值及主方向。

1 多孔非稳定抽水试验求参数的理论与方法

本文研究内容为通过定流量非稳定流抽水试验资料即已知地下水水位及流量反求目标含水层参数。周志芳在参考I.S.Papadopulos, M.S.Hantush和S.Way的研究成果后，依据泰斯公式，通过坐标轴的旋转、压缩变换提出，当有3口观测井在不同时刻的降深资料时，计算各向异性渗透系数张量主值和主方向的公式[10]

(1)

式中：s表示降深；Q表示流量；t表示时间；δ表示含水层厚度；Kx表示渗透系数在X轴方向的分量；Ky表示渗透系数在Y轴方向的分量；θ表示坐标系XOY顺时针旋转变换的角度。

该公式表明，s与lnt呈线性关系。对于任一观测井由直线斜率i，可以得

(2)

设第k(k=1,2,3)个观测井的井位为(Xk，Yk)，且对应s-lnt直线在零降深上的截距为[tk]，则由公式得

(3)

(4)

(5)

令Pyk=(xksinθ+kkcosθ)2，Pxk=(xkcosθ-yksinθ)2，带入上式中可整理为

[t1]2(Py2Px3-Py3Px2)+[t1][t2](Py3Px1-Py1Px3)+[t1][t3](Py1Px2-Py2Px1)=0

(6)

设

f(θ)=[t1]2(Py2Px3-Py3Px2)+[t1][t2](Py3Px1-Py1Px3)+[t1][t3](Py1Px2-Py2Px1)

(7)

设

F(θ)=[f(θ)]2≥0

当θ=θ*(精确解)时，F(θ)取得极小值(0)，即求目标函数

E(θ)=minF(θ) (A0≤θ≤B0)

的最优解。A0和B0为θ角变化的范围，在此设为0°和90°。根据求得的θ角，可带入公式(3)、(4)、(5)，从而计算出Ky与Kx的比值。

利用抽水试验数据带入理论公式具体步骤如下：

a.利用降深s与时间t半对数曲线获取各观测孔所对应的截距[tk](k=1,2,3)。

b.将[tk](k=1,2,3)和各观测孔坐标(Xk，Yk)代入式(7)和(8)，得到渗透系数张量的主要方向θ值。

c.将θ值带入式(3)、(4)、(5)联立对比最终得到Ky/Kx。

通过使用Matlab 2014将上述理论公式程序化，可直接输入各监测孔坐标和对应截距而得出渗透系数张量方向θ值和Ky/Kx，这样简化了计算工作量，并且提高了计算效率和准确性，程序计算流程见图1。

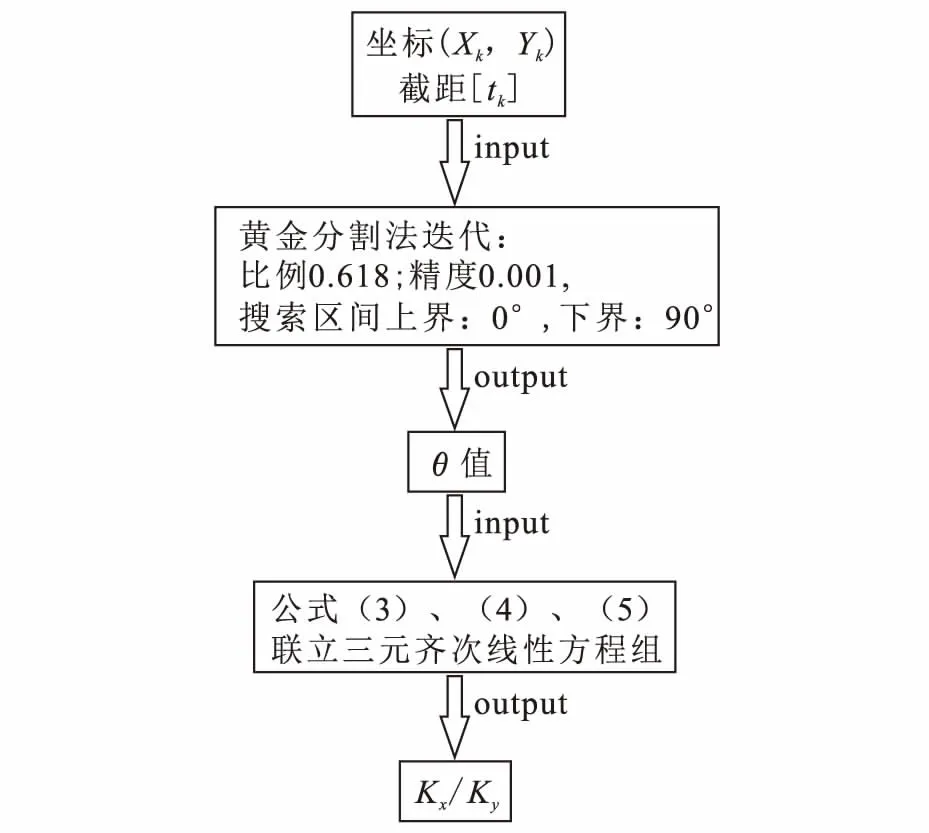
图1 Matlab程序计算流程Fig.1 Calculating process of Matlab

2 计算实例

2.1 试验场地及试验过程

试验场地位于重庆市渝北区，共布设4口钻孔(图2)，以抽水孔ZK1为原点，确定3个观测孔坐标(表1)。试验场地覆盖层厚1.5 m，下伏地层岩性为砂泥岩互层的单斜地层，倾角lt;10°，为缓倾角岩层，与上述公式的含水层产状近似水平的基本条件一致。第一层泥岩厚约15 m，目标含水层砂岩层厚约25 m(图3)。

在此共进行9次抽水试验，水位降深值由仪器Diver自动记录，文中选取其中2次试验数据进行计算，2次试验s-t曲线见图4。

图2 试验场地平面图Fig.2 Plane map showing experiment site

图3 试验场地剖面图Fig.3 Profile of experiment site

试验一于2016年8月15日9时30分开始，8月16日11时00分停止抽水，持续时长25.5 h，平均抽水速率3.17 m3/h。抽水孔ZK1内最大降深为2.68 m；各观测孔ZK2、CK1、CK2内的最大降深分别为2.42 m、2.43 m、2.55 m。

由s-t曲线可以看出，试验一进行过程中，曾在500～900 min时间段内水位发生震荡，根据Q-t曲线基本可以判断是由于水泵功率不稳定，在这段试验过程中，流量起伏过大而造成，但对整体试验结果无实质性影响。

图4 试验一与试验二s-t及Q-t曲线Fig.4 Q-t and s-t curves of Test 1 and Test 2

试验二于 2016年8月19日12时10分开始， 8月20日6时10分停止抽水，持续时长18 h。累计抽水量273.43 m3，平均抽水速率3.15 m3/h。抽水孔ZK1内最大降深为4.1 m，各观测孔ZK2、CK1、CK2内的最大降深分别为3.51 m、3.54 m、3.51 m。

2.2 各向异性渗透参数求解

本文计算各向异性渗透参数的核心在于作出降深值(s)与时间(t)的半对数曲线，以获取能够直接带入Matlab程序中进行迭代计算的s-lnt直线在零降深上的截距为[tk](k=1,2,3)，在此两次试验统一设监测孔CK1截距为[t1]，ZK2为[t2],CK2为[t3]。

分别作出试验一与试验二的s-lnt曲线(图5)。从图中可以看出，s-lnt的完整曲线是随时间的增加逐渐趋近为一条直线，而并非绝对的直线。从图中所作虚线可以看出，s-lnt曲线的斜率实际上需要确定一个有效范围，而这样会导致其截距也产生了相应的取值区间，并且2个s-lnt曲线都能看出CK1与ZK2曲线基本重合，所以在确定各观测孔对应截距取值区间时，可取[t1]= [t2]。

试验一中，根据曲线确定[t1]和[t2]取值区间为[55, 60]，[t3]取值区间为[45, 50]。为提高计算效率，截距取值均取整数。将所有取值组合输入程序，最终得到以下计算结果(表2)。

试验二中，确定[t1]和[t2]取值区间为[30,35]，[t3]取值区间为[25, 30]。将数据带入程序中运行得到结果见表3。

图5 试验一与试验二s-lnt曲线Fig.5 s-lnt curves of Test 1 and Test 2

[t3][t1]454647484950θKy/KxθKy/KxθKy/KxθKy/KxθKy/KxθKy/Kx5518.013.215.010.012.08.59.07.76.07.44.07.25620.519.317.017.514.59.611.08.39.07.76.07.45723.043.020.017.217.011.614.09.311.08.28.67.65819.015.616.511.013.69.110.88.05821.726.219.014.416.010.613.08.96024.0112.021.022.018.013.415.010.0

2.3 数据讨论

据表2结果，各向异性渗透张量的主要方向θ取值范围为[4°, 24°]，Ky/Kx取值范围为[7.2, 112]。而据表3结果，θ值对应取值区间为[1°,24°]，Ky/Kx取值区间为[7.3, 254]。2次试验计算结果取其交集为θ值取值区间为[4°, 24°]，Ky/Kx取值区间为[7.3, 112]。但考虑抽水试验各观测孔的实际降深情况及泰斯公式自身的局限性，区间内仍存在部分取值范围不合理。结合实际抽水试验过程，最终确定θ值范围为[8°, 18°]，Ky/Kx值范围为[7.5, 13] 。

四川盆地红层分布区构造作用较弱的缓倾斜砂岩岩体，其渗透性各向异性三维特征主要受控于岩层产状，呈现出以岩层倾向、走向和法向为三向渗透优势主方向，统计上显示以倾向与走向为渗透性最强的2个主要优势方向，法向(一般多为垂向)一般为最小渗透优势方向。本文计算结果推测出该区域岩体渗透性存在较明显的方向性，其优势方向为近南北向，这与研究区砂岩地层走向一致，显示的是岩层走向的主控作用。

表3 试验二计算结果Table 3 Calculating results of Test 2

3 结 论

a.运用Matlab将公式程序化是使用黄金分割法迭代计算参数最高效的方式之一。

b.通过多孔非稳定抽水试验，运用试验参数成功反求各向异性渗透参数，将2次试验数据的反求结果对比分析得到以下结果：渗透系数张量的方向θ值范围为[8°, 18°]，Ky/Kx的取值范围为[7.5, 13]。

c.在计算过程中，参数的取值尤为关键，由于s-lnt曲线并不完全是一条直线，而是越来越趋近于直线，这样会导致曲线在零降深上的截距取值为一个区间而非唯一值。

d.s-lnt曲线在零降深上的截距是一个敏感度极高的参数，参数值的微小变化甚至可以导致Ky/Kx发生大于10倍的变化，因此确定其有效取值范围是极为重要的。

e.本文研究的目标含水层实际为潜水，虽不完全满足泰斯公式的承压含水层条件，但计算结果与实际各钻孔水位降深情况基本吻合，这样的计算理论是适用的。

[1] Papadopulos I S. Nonsteady flow to a well in an infinite anisotropy aquifer[J]. Symposium of Dubrovnik, 1965, 1: 21-31.

[2] Huntash M S. A method for analyzing a drawdown test in anisotropic aquifer[J]. Water Resources Research, 1966, 2(2): 281-285.

[3] Way S C. In-situ determination of three-dimensional aquifer permeabilities[J]. Ground Water, 1982, 20(5): 595-603.

[4] Neuman S P, Walter G R, Bentley H W,etal. Determination of horizontal aquifer anisotropy with three wells[J]. Ground Water, 1984, 22(1): 66-72.

[5] 田开铭,万力.各向异性裂隙介质渗透性的研究与评价[M].北京:学苑出版社, 1989.

Tian K M, Wan L. Research and Evaluating of Anisotropic Fissured Medium Permeability[M]. Beijing: Xueyuan Publishing House, 1989. (in Chinese)

[6] 周志芳,朱学愚,李艳.岩体渗透系数张量的半解析计算[J].水利学报,1997(9):6-11.

Zhou Z F, Zhu X Y, Li Y. Semi-analytic method for conductivity tensor in rock mass[J]. Journal of Hydraulic Engineering, 1997(9): 6-11. (in Chinese)

[7] 周志芳,庄超,戴云峰,等.单孔振荡式微水试验确定裂隙岩体各向异性渗透参数[J].岩石力学与工程学报,2015,34(2):271-278.

Zhou Z F, Zhuang C, Dai Y F,etal. Determining anisotropic hydraulic conductivity in fractured rocks based on single-borehore slug tests[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(2): 271-278. (in Chinese)

[8] 许模,黄润秋.岩体渗透特性的渗透张量分析在某水电工程中的应用[J].成都理工学院学报, 1997,24(1):56-63.

Xu M, Huang R Q. Application of permeability tensor analysis to study rock mass permearbility of a certain hydroelectric project in southwest of China[J]. Journal of Chengdu University of Technology, 1997, 24(1): 56-63. (in Chinese)

[9] 刘青泉,樊红光.二维裂隙渗流等效渗透系数张量的一种近似算法[J].力学与实践,2012,34(5):16-20.

Liu Q Q, Fan H G. An approximate method for calculating the equivalent permeability tensor of seepage in complicated fractures[J]. Mechanics in Engrneering, 2012, 34(5):16-20. (in Chinese)

[10] 周志芳,王锦国.地下水动力学[M].北京：科学出版社,2013:135-137.

Zhou Z F, Wang J G. Groundwater Dynamics[M]. Beijing: Science Press, 2013: 135-137. (in Chinese)

Calculationofanisotropicpermeabilityparametersofflatpitchaquiferbasedonmultiple-wellunsteadypumpingtest

JIANG Bing1,2, TANG Yige1, XIA Qiang1, XU Mo1

1.StateKeyLaboratoryofGeohazardPreventionandGeoenvironmentProtection,ChengduUniversityofTechnology,Chengdu610059,China;2.ChongqingChengdeGeotechnicalEngineeringInvestigationCo.Ltd,Chongqing401147,China

The parameters of anisotropy of hydrogeology can be obtained through drawdown-time relationship of multiple-well pumping test. In this paper, the multiple-well unsteady pumping test data are used to calculate the main direction and specific value of permeability tensor by Matlab incorporating with non-axial anisotropic permeability tensor theory. The final result which is consistent with the actual drawdown condition is obtained after contrastive analysis from two separate test results, with the main direction range of [8°, 18°], and theKy/Kxrange of [7.5, 13]. The calculation method proves to be feasible and rational for the non-axial anisotropic permeability tensor theory. It points out that the key parameter to calculate anisotropic permeability parameters is the intercept ofs-lntcurve.

pumping test; layered aquifer; anisotropy; permeability tensor

P641.2

A

10.3969/j.issn.1671-9727.2017.06.13

1671-9727(2017)06-0756-06

2017-01-16。

国家自然科学基金青年基金项目(41502237)。

江冰(1963-)，男，高级工程师，研究方向：水文地质与工程地质, E-mail:448124138@qq.com。