利用 -t图透视各类碰撞

马永毅

(河北辛集中学,河北 辛集 052360)

·问题讨论·

马永毅

(河北辛集中学,河北 辛集 052360)

本文将利用v-t图展示不同类型的碰撞,同时系统总结了所涉及到的关于碰撞的规律,具体包括3类： (1) 根据恢复系数不同划分的3类碰撞; (2) 根据两球质量不同划分的5类碰撞及其相关的二级结论; (3) 根据两球速度不同划分的5类碰撞,并着重研究了不同碰撞相互转换的条件及方法.

碰撞;速度-时间图像;类型

在高考试题中以碰撞为背景的试题较多,但碰撞的种类繁多,与碰撞相关的二级结论也比较多,而研究碰撞问题应用的规律主要是动量守恒、能量守恒.这两个规律又是高考的重点、热点.有效地掌握这些类型各异的碰撞、熟练地应用碰撞的规律,需要对碰撞有更深刻系统的认识.本文将利用v-t图展示不同类型的碰撞,同时系统总结了所涉及到的有关碰撞的二级结论,使学生对碰撞有更深刻的理解.

1 根据恢复系数不同划分的3类碰撞

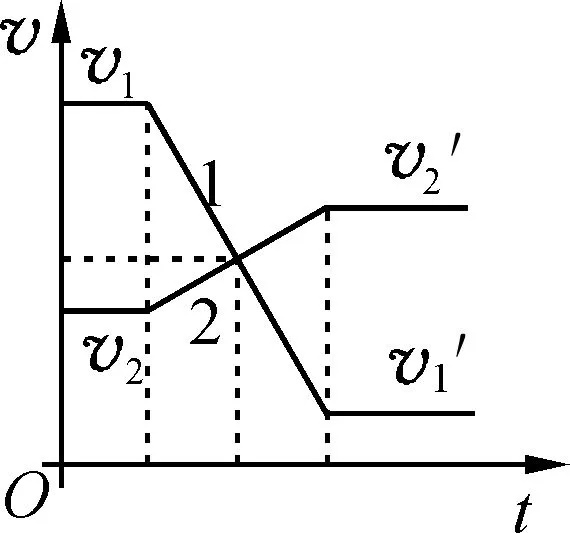
图1

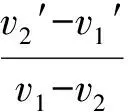
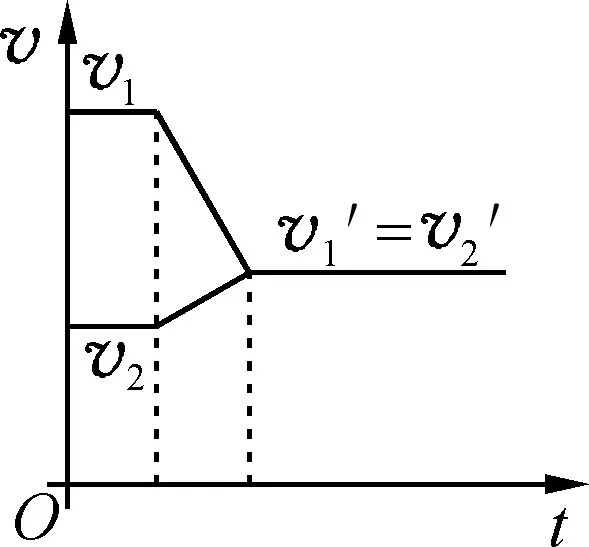
图3

2 根据两球质量不同划分的5类碰撞

针对完全弹性碰撞,两球质量不同造成的结果也将不同.

(1) 质量相等的两个小球发生完全弹性碰撞,结果交换速度.

如图5所示,由于两球质量相等,1线段、2线段的斜率大小相同,整个图形相对于虚线pt0对称,可得两球碰后交换速度.

(2)m1gt;m2,两个小球发生完全弹性碰撞,如图6所示,1线段斜率的大小小于2线段的斜率,整个图形相对于p点对称.

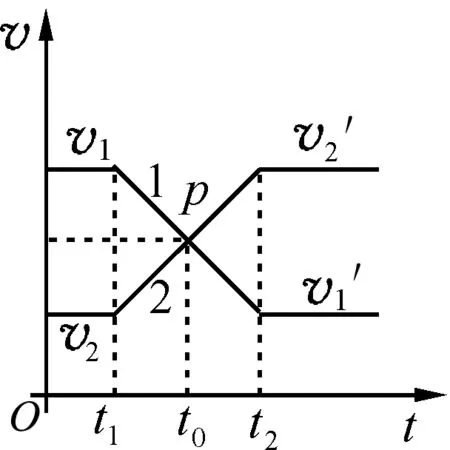
图5

(3)m1lt;m2,两个小球发生完全弹性碰撞,如图2所示,1线段斜率的大小大于2线段的斜率,整个图形相对于p点对称.

(4)m1≫m2,也就是质量非常大的1球追上质量非常小的2球发生完全弹性碰撞,如图7所示,1线段斜率趋于0,2线段斜率趋于无限大,碰撞时间t1到t2也非常短,结果,1球速度几乎不变v1′≈v1,2球被碰后速度增加了碰前两球相对靠近速度的2倍,v2′≈v2+2(v1-v2).如图8所示,如果碰前2球速度为0,则v1′≈v1,v2′≈2v1,即碰后1球速度几乎不变,2球获得1球速度2倍.

图7

(5)m1≪m2,也就是质量非常小的1球追上质量非常大的2球发生完全弹性碰撞,如图9所示,1线段斜率趋于无限大,2线段斜率趋于0,碰撞时间t1到t2也非常短,结果,2球速度几乎不变v2′≈v2,1球碰后速度减少了碰前两球相对靠近速度的2倍,v1′≈v1-2(v1-v2).如图10所示,如果碰前2球速度为0,则v1′≈-v1,v2′≈v2,即碰后1球被原速率反弹,2球速度几乎不变.

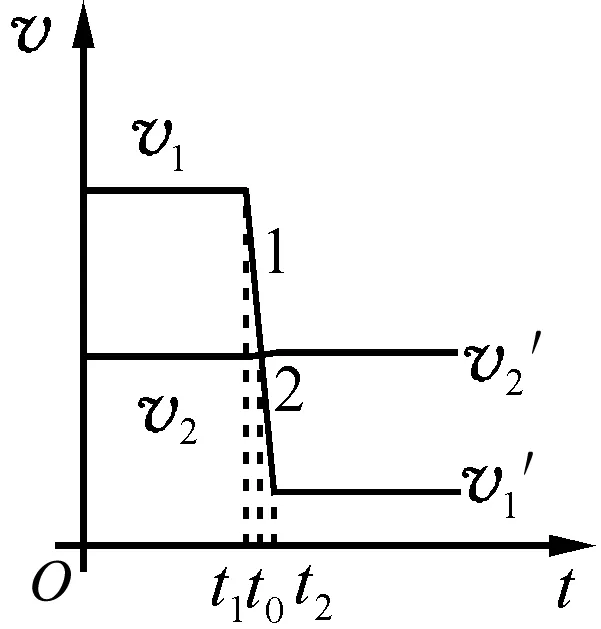
图9

3 根据两球速度不同划分的5类碰撞

(1) 碰前碰后速度各异的5类碰撞,以完全弹性碰撞为例.

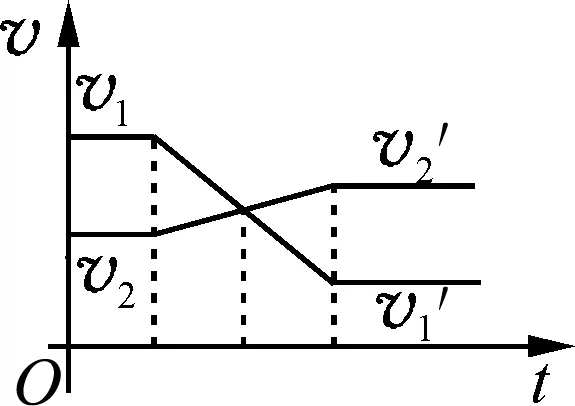
图11

第一类:碰前两球速度同向,碰后两球速度均沿该方向,如图11所示.

第二类:碰前两球速度同向,碰后1球速度反向,如图12所示.

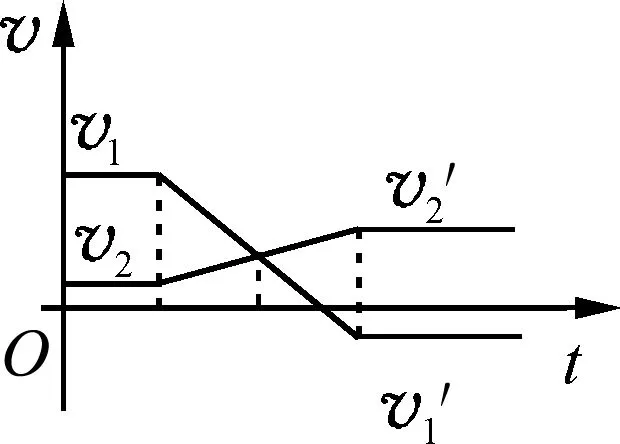
图12

图14

第三类:碰前2球速度为0,碰后1球速度反向,如图13所示.

第四类:碰前两球相向运动,碰后两球均反向运动,如图14所示.

第五类:碰前两球相向运动,碰后两球同向运动,如图15所示.

(2) 两球两次碰撞程度完全相同的条件.

只要有确定质量、确定材料的两个小球相对速度相等,无论两球碰前是同向还是反向,无论两球碰前速度为多大,无论两球发生的是完全弹性碰撞、完全非弹性碰撞还是非完全弹性碰撞,也无论两球质量差距是多少,两球的碰撞时间、碰撞的程度是完全相同的.

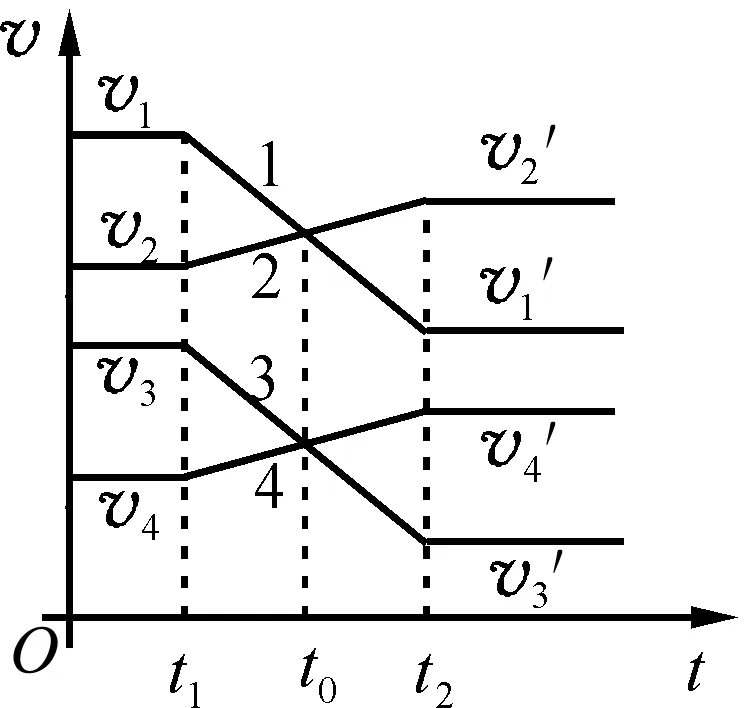
图16

如图16所示,设质量确定的两个球发生了两次完全弹性碰撞,碰前其相对速度相等v1-v2=v3-v4.由v-t图可判断这两次碰撞只是图形整体上下平移而已,其余无任何差距,进而可推得两次碰撞时间相同,碰撞的情况也相同.

(3) 两球两次碰撞相互转换的方法.

从v-t图上观察可以得到一个结论,两次碰撞碰前相应球速度的差值与碰后相应球速度的差值均相等,即v1′-v3′=v1-v3=v2′-v4′=v2-v4=Δv,其中Δv是两次碰撞相互转换的关键量.这样只要质量及材料确定的两个球碰前相对速度相等,就可以利用Δv将一种碰撞转换成另一种碰撞.

根据上述的推导,结论是否成立与碰撞究竟属于弹性碰撞还是非弹性碰撞无关,因此对这些碰撞均适用;两球质量的差距只影响图线的倾斜程度,也不影响结论的成立.

(4) 通过转换对复杂的碰撞进行简化.

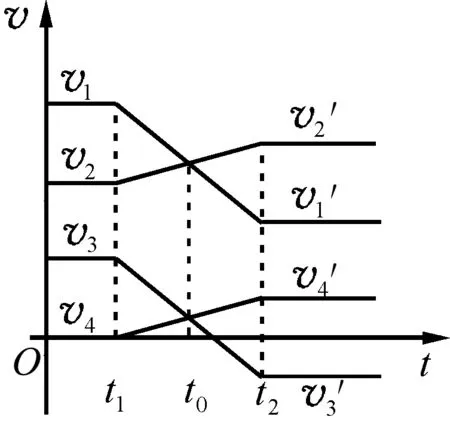
图17

既然有确定质量、确定材料的两个小球相对速度相等,碰撞的情况就完全相同,就可以进行两次碰撞的相互转换,因此所有复杂的碰撞都会对应自己的一动碰一静的简单的碰撞如图17所示.

1 漆安慎，杜婵英.力学[M].北京： 高等教育出版社,1997： 180-188.

2017-05-12)