基于可扩展多目标蚁群算法的土地利用优化配置
2017-12-01莫致良杜震洪张丰刘仁义
莫致良,杜震洪*,张丰,刘仁义
(1. 浙江大学 浙江省资源与环境信息系统重点实验室, 浙江 杭州 310028; 2. 浙江大学 地理信息科学研究所, 浙江 杭州 310027)
基于可扩展多目标蚁群算法的土地利用优化配置
莫致良1,2,杜震洪1,2*,张丰1,2,刘仁义1,2
(1. 浙江大学 浙江省资源与环境信息系统重点实验室, 浙江 杭州 310028; 2. 浙江大学 地理信息科学研究所, 浙江 杭州 310027)
传统的土地利用优化配置模型无法灵活应对现实场景中多变的优化目标要求,也无法实现土地利用在空间布局上的优化.根据常见的优化目标进行抽象建模,建立了可扩展的多目标体系,并与蚁群算法有机结合,构建了基于可扩展多目标蚁群算法的土地利用优化配置模型,使土地利用配置在不同目标的指导下能够灵活优化,同时实现了土地利用配置在数量结构和空间布局优化上的统一,为土地利用规划提供了更具现实意义的参考方案.最后对该模型,以杭州市萧山区2015年土地利用格局为基础数据进行实例验证.结果表明: 模型能够在多目标体系的指导下,合理配置研究区域的土地利用结构与布局,促进区域土地利用的可持续发展,并针对不同的多目标体系,给出具有不同侧重点的优化方案.
土地利用优化配置;蚁群算法;可扩展的多目标体系
土地资源是人类生产活动最基本的物质资源,合理利用有利于促进社会经济发展、保障粮食安全以及保护生态环境.人口增长和城市化进程的加快,带来了发展与保护的双重任务、资源利用与生态保护的双重压力[1],导致土地资源的供需矛盾越发突出.在我国,土地资源的不合理利用已经造成了严重的社会和环境问题,成为制约可持续发展的“瓶颈”[2-3].因此,优化土地利用配置,实现土地的可持续利用和社会的可持续发展,是摆在国人面前的重要任务.
蚁群优化算法(ant colony optimization,ACO)是受自然界中蚂蚁觅食行为的启发而建立的一种启发式算法[4],最早由意大利学者DORIGO等[5]提出,并迅速发展为一种通用的优化方法.ACO最早用于解决旅行商问题[5-6](traveling salesman problem,TSP),后期发展出了MMAS、EAS、AS等多种改进形式,并被广泛用于解决各类组合优化问题,如刘建华等[7]提出了基于势场蚁群算法的移动机器人路径规划方法,可有效加快机器人的路径寻优速度并提高搜索能力,而李倩等[8]和高晋凯等[9]分别将蚁群算法应用于扩展约束P-中位和图像分割问题,均得到了良好的优化结果.
在土地利用优化配置方面,国内外学者已进行了比较多的探索,从优化配置的方法来看,主要分为2种: DAS等[10]、徐磊等[11]、黄海[12]分别采用线性规划、系统动力学和粒子群算法等对区域土地利用的结构和数量进行优化;CHEN等[13]、袁满等[14]和LIU等[15]则分别采用模拟退火、多智能体遗传算法和粒子群算法进行土地利用优化配置,解决了土地利用的空间布局优化问题.另外,高小永[1]建立了基于多目标蚁群算法的土地利用优化配置模型,并与GIS系统结合,实现了模型在实际场景下的应用.以上方法均是在特定目标体系下进行的研究,而土地利用优化配置是一个复杂的多目标优化问题,不可变的目标体系无法对特定规划目标给出优化方案,不能满足现实场景中复杂的多目标需求,从而限制了模型的推广应用.
本文将基本的单目标蚁群算法与多目标体系相结合,针对多目标决策技术与土地利用空间布局优化的特点,提出基于可扩展多目标蚁群算法的土地利用优化配置模型,并选取杭州市萧山区为研究区域,在不同的多目标体系下进行土地利用的优化配置,通过比较不同多目标体系下的优化结果,验证模型的有效性.
1 基于可扩展多目标蚁群算法的土地利用优化配置模型
在模型中,将研究区域处理为I行J列的二维格网矩阵,每个格网表示长、宽均为Lm的土地单元;共分K种土地利用类型,需要分配的土地利用类型有耕地、绿地、建设用地、林地和未利用地5种.每只蚂蚁ant包含禁忌表(tabu)、配置方案(tours)和各目标函数值(targs).由于每只蚂蚁对应一种优化配置方案,因此,搜索优化配置方案解集的过程,即为确定蚂蚁代表的配置方案为Pareto最优解的过程.
1.1 研究思路
建立基于可扩展多目标蚁群算法的土地利用优化配置模型,首先建立基本的多目标体系,对目标进行抽象建模,建立可扩展的多目标体系;其次将蚁群算法与多目标体系相结合,须对基本蚁群算法的核心函数进行改进,使其满足多目标优化的要求;最后将改进后的多目标蚁群算法与土地利用优化配置相结合,根据土地利用优化配置的多目标体系与约束体系,完成模型的构建.
1.2 可扩展多目标体系的构建
土地利用优化配置是一个复杂的多目标优化问题,而指导优化的多目标体系是一个动态扩展的体系.从历史来看,土地利用优化配置早期仅考虑区位经济目标,而如今逐步扩展,已经涵盖了社会目标和生态目标,因此多目标体系会随社会发展而逐渐扩展.在现实条件下,由于土地利用优化配置涉及多个行业和部门的利益,可以通过不同的指标来表示其用地需求,这些指标种类丰富而难以充分涵盖,可能随时间而增加或减少,因此需要多目标体系以动态、灵活地适合这种需求.
理论上讲,各行各业最基础的物质资源是土地资源,它们对不同土地利用类型的用地需求,可通过不同的指标表征,这些指标共同构成土地利用优化配置的目标体系,因此,均可成为扩展目标.然而,在当前阶段,由于指标的复杂性,通过多目标体系难以准确模拟社会的真实情况,则根据优化配置目的选择扩展目标较为合理,常见的扩展目标有生态服务价值目标、碳排放量目标等,具有针对性的目标还有土地退化评价目标、景观生态安全评价目标等.
可扩展的多目标体系,由基本的多目标体系和扩展目标体系共同构成.其中基本多目标体系由土地适宜性目标、空间集聚目标和最小规划成本目标3个基本目标共同构成,缺一不可.根据格网数据结构和土地利用类型,参考3种基本目标,建立相应的扩展目标模型,进而将不同指标按照模型完成建模,并根据实际需要加入扩展目标体系,即将扩展目标文件放入目标体系所在的目录.本文所有目标均以L表示.
基本的多目标体系由土地适宜性目标、空间集聚目标和最小堆成本目标构成,基本目标的建立如下所述:
(1) 土地适宜性目标L1
由于土地单元具有空间异质性,即使是同一土地单元,对不同的地类也具有不同的适宜度,因此在全面分析土地状况的基础上进行土地适宜性评价,并以此为基础进行土地利用优化配置,是土地利用优化配置的科学基础,也是土地利用空间布局优化实现的保证.本文采用AHP方法得到研究区域内每个格网对耕地、绿地、森林和建设用地的适宜度,并定义目标函数为
(1)
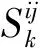
(2) 空间集聚目标L2
根据经济地理学的集聚效应,将相同地类的土地尽可能集聚在一起,实现资源、要素和经济活动在空间中的集聚,可以降低成本,创造更高的经济效益[16],因此提高区域地类的集聚程度,应该作为土地利用优化配置的一项优化目标.根据格网i,j处土地利用类型是否为k,定义二值函数:
(2)
其中uij为格网(i,j)处的土地利用类型,则(i,j)处土地利用类型k的邻域同一性指数为
(3)
其中(i,j)≠(s,t),这里采用八邻域作为窗口,则空间集聚目标函数定义为
(4)
(3) 最小规划成本目标L3
在土地利用优化配置过程中,土地单元的类型因重新配置而发生转换,从而产生转换代价,以最小的代价获得最高的综合效益符合规划目的,因此最小化规划成本应该作为优化配置的目标之一.
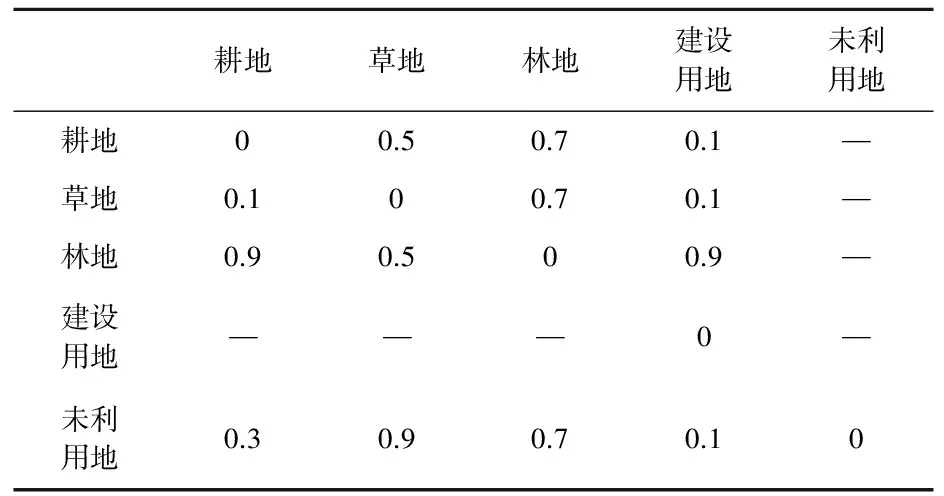
由于不同土地利用类型之间的转换成本难以获取,本文通过AHP方法确定不同土地利用类型之间的转换因子,对转换因子进行归一化处理.由于最小规划成本为最小化问题,这里考虑将其转为最大化问题.因此,在最小规划成本目标下,(i,j)处的土地单元从土地利用类型k转为类型p的目标函数为
(5)
其中Ckp表示从地类k转化为地类p的成本,则最小规划成本目标函数:
(6)
在扩展多目标体系中,由于可能的扩展目标种类多而难以预测,因此从格网的数据结构出发,抽象出3种可能的扩展目标模型如下:
(1) 适宜度类型扩展目标L4
适宜度类型扩展目标是用单因子目标或多因子综合目标在对研究区域进行评价的基础上,对区域内所有的土地单元分别计算不同地类的适宜度.这种扩展目标在每个格网的各个地类上均有相应的适宜度,因此是最详细的目标类型,可以从空间上对土地利用配置进行优化指导.土地适宜度评价目标是适宜度类型扩展目标的基础模型.每个土地单元上的适宜度类型扩展目标的属性结构如表1所示.
表1 适宜度类型扩展目标的结构

Table 1 Structure of extensible target of suitability type
其目标函数采用类似适宜度评价的目标函数,定义为
(7)

(2) 转换类型扩展目标L5
转换类型扩展目标是对不同土地利用类型之间的转换给目标带来促进或抑制的定量描述.理想条件下,任何目标都可以在空间上指导土地利用的优化配置,然而,在现实场景下,很多目标往往因为数据难以获取或难以量化等原因,无法对每个格网上的土地利用类型转换都进行定量描述,而只能从整体上,对不同土地利用类型之间的转换进行模拟,而最小规划成本就是转换类型扩展目标的基础模型.这种类型的扩展目标的属性结构如表2所示.
表2 转换类型扩展目标的结构

Table 2 Structure of extensible target of transform type
转换类型扩展目标的函数定义为
(8)
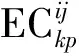
(3) 价值类型扩展目标L6
类似地,价值类型扩展目标也无法为每个土地单元的不同土地利用类型提供量化描述,只能对研究区域内每种土地利用类型在整体上进行定量描述,这种价值可能是正价值,也可能是负价值,因此价值类型扩展目标可能是最小化问题,需要先将目标处理为最大化问题,并做归一化处理.这种类型的扩展目标没有出现在基本目标中,但作为一种可能出现的目标类型,应该对其进行抽象建模.价值类型扩展目标的属性结构如表3所示.
表3 价值类型扩展目标的结构

Table 3 Structure of extensible target of value type
因此,价值类型扩展目标的函数定义为
(9)

1.3 蚁群算法与多目标体系的融合
将多目标体系与蚁群算法相结合,需要改进蚁群算法的核心函数,主要包括启发信息函数η(t)、信息素释放函数Δτ(t)和概率转移函数p(t).
(1) 启发信息函数
设在第t次迭代时,第a只蚂蚁在格网(i,j)处将地类从k转为p,在单目标L下的启发信息函数为η(t),则目标L在(i,j)处的目标函数值fL有
(10)
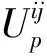
(11)
其中sp为目标L与L2的平衡系数.因此,在多目标体系下,启发信息函数定义为
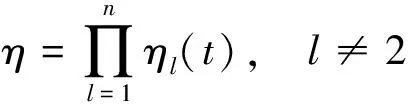
(12)
(2) 信息素更新函数
GOSS等[17]的研究表明,蚂蚁会在经过的路径上留下信息素,相同时间内,较短的路径上信息素挥发较少,而蚂蚁倾向于选择信息素浓度高、路径短的路径,从而实现蚁群的正反馈机制.模拟这一正反馈机制的算法即为蚁群算法.其中的关键函数就是信息素更新函数τ(t)和信息素释放函数Δτ(t).蚁群算法与多目标体系结合时,信息素释放函数定义为
(13)
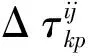
(14)
其中,ρ为信息素挥发因子,N为蚁群规模.
(3) 概率转移函数
在土地利用优化配置过程中,当前土地单元配置为其他类型时,仅在当前土地单元发生,而不会造成邻域的土地单元也发生类型转换,因此只需考虑当前格网从当前地类转为其他地类的概率即可,其概率转移函数为
(15)
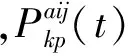
1.4 构建基于可扩展多目标蚁群算法的土地利用优化配置模型
本文对多目标体系进行抽象建模,建立了可扩展的多目标体系,将其与蚁群算法结合,应用于土地利用优化配置,建立了基于可扩展多目标蚁群算法的土地利用优化配置模型.模型流程如图1所示.
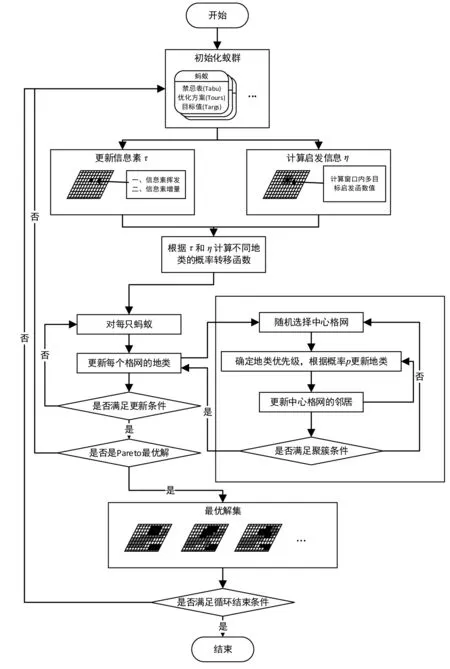
图1 基于多目标蚁群算法的土地利用优化配置模型流程图[18]Fig.1 Flow chart of land use optimizing allocation based on multi-objective ant colony algorithm
在模型基础上,本文使用JAVA语言完成了模型的实现,模型流程的伪代码如下:
Opti opti= new Opti ();
//读取数据
opti.instance = opti.inOut.read_data(path);
//初始化蚁群和参数
opti.init ();
while (判断终止条件) {
//蚁群构造优化配置方案
if (opti.simulateAnts()){
//选择最优解,更新信息素
opti.updatePheros ();
//重新初始化蚁群
opti.restartAnts ();
}
}
//输出Pareto最优解集
opti.inOut.output();
在上述伪代码中,综合考虑性能和优化结果,设置终止条件为最少80次迭代周期,同时要求在最后的20次迭代中最优解无更新.
在蚁群算法与多目标体系融合的过程中,启发信息函数是融合的关键,蚂蚁a在格网p处将土地利用类型配置为type,计算启发信息函数目标的伪代码如下:
if (判断是否符合约束规则) {
double res = 1.0;
for (遍历所有目标) {
//计算目标在位置p的启发信息值
res *=e.getValue().eta(p, type, grids);
}
//更新配置方案在p处类型type的启发信息
grids[p.x][p.y].exp.replace(type, res);
return res;
} else {
return 0;
}
在构建的模型中,信息素更新是蚁群算法正反馈机制的关键,模型中信息素更新和蚁群信息素释放的伪代码如下:
//遍历整个格网和不同地类,更新信息素
for (intl=0;l // 信息素挥发 ph.pheroVolat(i,j,l); for(intk=0;k if(蚂蚁改变了格网的地类类型){ 蚂蚁释放信息素 } } } 可扩展多目标体系的灵活性,在于对不同目标的优化或对不同指标进行选择时,可以独立构建、添加或删除具有针对性的扩展目标,而不需要对多目标体系的其他部分进行调整. 本文以杭州市萧山区为研究区域,进行实例验证.在完成模型的构建后,首先在传统无扩展目标的基本多目标体系(简称M1)下进行实验验证.由于可扩展多目标体系的灵活性,本文单独构建了转换类型的碳排放量目标和价值类型的生态服务价值目标,从而形成4种不同的多目标体系,分别为添加碳排放量的多目标体系M2、添加生态服务价值的多目标体系M3和添加碳排放量与生态服务价值的综合多目标体系M4.然后,在不同的多目标体系下分别进行实验,最后对优化配置方案进行对比,验证模型的有效性. 2.1 研究区域介绍 萧山区位于杭州市南部,2001年3月撤市设区,西北临钱塘江,地理坐标为120°04′22″E~120°43′46″E,29°50′54″N~30°23′47″N.萧山区下辖15个镇,11个街道,辖区总面积1 420.22 km2.南部以低山丘陵为主,中北部主要为平原,地区内平原约占66%,山地约占17%.属亚热带季风性气候,雨量充沛.截至2014年末,户籍登记人口125.54万,生产总值1 728.32亿元,三大产业结构比例为3.5∶54.1∶42.4,人均GDP达到138 309元. 2.2 数据收集与多目标体系设置 研究区域数据有统计数据、遥感数据、空间数据3类.统计数据,主要包括2014年各城镇、街道的常住人口、自营出口额,来自萧山区统计年鉴;遥感数据,主要包括SRTM DEM数据、DMSP/OLS灯光数据;空间数据为2015年萧山区1∶10 000土地利用数据.通过ArcMap软件,将数据处理为200 m×200 m的格网,共计35 335个.并根据数据提取地形、经济和自然因子,形成土地适宜性因子评价表,最终得到所有格网的土地适宜性评价结果. 对于最小规划成本目标,由于不同土地利用类型之间的转换成本难以直接获取,则参考文献[3]提出的用土地利用类型转换系数来间接反映转换成本,最后不同土地利用类型之间的转换成本如表4所示. 表4 最小规划成本中的地类转换因子 Table 4 Conversion factor between land use types in minimum planning cost target 注—表示无相应的转换因子. 对于碳排放量扩展目标,根据文献[19-20]对不同生态系统与碳排放量关系的研究,得到不同土地利用类型的碳排放/吸收系数,处理得到不同土地利用类型转换过程中引起的碳排放/吸收量矩阵,如表5所示. 表5 碳排放量目标中的地类转换因子 Table 5 Conversion factor between land use types in carbon emission target 根据文献[21]的研究,得到不同土地利用类型代表的生态服务价值,如表6所示. 表6 生态服务价值目标中的地类价值因子 Table 6 Value factor of land use type in ecological service value target 2.3 蚁群算法参数设置 模型中蚁群算法的重要参数均为基本蚁群算法的参数,其取值与土地利用优化配置无关,本文根据多次试验的模拟优化配置结果,参数设置如表7所示. 表7 蚁群算法参数设置 Table 7 Parameter setting of ant colony algorithm 2.4 结果与分析 在不同的多目标体系下进行土地利用优化配置,分别得到相应的优化配置解集,并选取解集中任一优化配置方案,与其他多目标体系下的优化方案做对比分析. 2.4.1 目标函数分析 在M1、M2、M3、M4四种不同的多目标体系优化配置方案下的各个目标函数的收敛情况如图2所示.可知,在不同的多目标体系下,各个目标函数都能在迭代过程中逐步优化,在搜索初期优化速度较快,后期则较慢,如M4下的空间集聚目标,初期以较快的速度优化,在迭代30次后,优化速度明显减慢,其土地适宜性目标也具有类似特点. 图2 M1/M2/M3/M4中各目标函数的优化曲线Fig.2 Optimizing curves of all targets in M1/M2/M3/M4注 横坐标为迭代次数,纵坐标为对应目标值. 不同的多目标体系下,各目标函数在优化过程中,对每次优化的贡献不同,这是由蚁群搜索过程中随机选择待优化格网造成的.同时,不同的优化配置方案,收敛到最大值的迭代次数不同,在M1和M4中,基本都在第40次迭代时完成收敛,而在M2和M3中,则在第60次迭代时才完成收敛.另外,在不同的多目标体系下,即使目标相同,最终收敛到的最大值也不相同,如碳排放量目标,在M2和M4中,最后收敛到的最大值分别为0.044 3和0.025 6. 2.4.2 土地利用数量结构分析 在不同的多目标体系下进行优化配置,得到不同的土地利用类型转换矩阵,如表8~11所示. 表8 M1中的土地利用类型转换矩阵 Table 8 Transform matrix of land use types in M1 表9 M2中的土地利用类型转换矩阵 Table 9 Transform matrix of land use types in M2 表10 M3中的土地利用类型转换矩阵 Table 10 Transform matrix of land use types in M3 表11 M4中的土地利用类型转换矩阵 Table 11 Transform matrix of land use types in M4 由以上4表可知,在M1中,耕地有明显转为建设用地和林地的趋势,分别有984个土地单元的耕地被建设用地占用,另有436个耕地单元退耕还林.因此在基本多目标体系下,萧山区土地利用优化配置,以建设用地占用耕地和退耕还林为主.M2的优化配置方案与M1非常类似,其中建设用地占用耕地的面积几乎相同,但注意到加入碳排放量目标后,林地与耕地碳排放量的差异,使得M2中退耕还林趋势比M1更明显,整体上M2中林地比M1多90个单元.与M1相比,M3增加了生态服务价值目标,因此M3与M1的优化配置结果相比,建设用地占用耕地的趋势在M3中被遏止,而且出现大规模退耕还林现象,因此M3中建设用地单元比M1减少了1 076个土地单元,而林地则比M1增加了726个单元.M4综合了M2与M3的特点,注意到M4的优化配置结果与M3非常类似,但相对而言,M4的耕地面积比M3略多,而林地面积有少量减少.因此,M4与M1的差异中起主要作用的是生态服务价值目标,碳排放量目标起次要作用. 不同多目标体系下,土地利用优化结果与优化前土地利用结构对比,如表12所示. 表12 不同多目标体系优化后的土地利用结构对比 Table 12 Comparison of land use structures after different multi-objective system’s optimizing 由不同多目标体系下的优化结果与优化前的对比可知,整体上表现为耕地面积占用比例减少,林地和建设用地占用比例增加的趋势,另外未利用地占用比例也有所减少,土地利用率有所提高. 注意到M1与M2、M3与M4中各地类比例相似,但两者之间差异较大.其中M2与M1优化后的比例结构相似,与M1相比,M2的耕地比例较小,而林地和建设用地比例有所增加;而M3与M4优化后的比例结构相似,但M4中耕地和建设用地的比例比M3中有所增加,而林地比例有所下降.因此认为在扩展目标中,生态服务价值起主要作用,而碳排放量起次要作用,由M3与M4的差异可知,碳排放量目标对生态服务价值目标有一定的抑制作用. 综上所述,在不同的多目标体系下,模型能对萧山区的土地利用结构进行调整优化. 2.4.3 土地利用空间布局分析 对不同多目标体系下的土地利用优化结果进行土地景观格局分析,分别从斑块密度、景观分离度指数和景观形状指数3个方面来评价优化配置结果的空间布局情况,如表13所示. 表13 不同多目标体系优化后的各地类景观指数统计对比 Table 13 Comparison of landscape indices of land use types after different multi-objective system’s optimizing 由表13可知,在不同的多目标体系下,优化后的耕地、建设用地、林地在斑块密度、分离度指数、形状指数3个指标上整体呈明显的减小趋势,表明优化配置后耕地、建设用地和林地的斑块形状更加规则,零散度更小,在空间中更加集聚.因此,不同的多目标体系下的模型都可以改善萧山区的土地利用状况,使土地利用空间布局更加合理. 在M1和M2中,建设用地集聚效应更为明显,体现了集约用地的要求,更有利于发挥土地的集聚效应,对经济发展更加有利,M2中碳排放量目标的存在,使得M2更侧重于发展和保护生态环境,而建设用地集聚程度较M1略小;在M3和M4中,更强调生态服务价值目标的作用,使得林地更加集聚,更有利于保护生态环境,改善区域的自然条件. 分析了土地利用优化配置中基本多目标的形式,将可能的目标分为3种基本类型,由此建立了可扩展的多目标体系,将其与蚁群算法结合,构建了基于可扩展多目标蚁群算法的土地利用优化配置模型,并选取杭州市萧山区为研究区域,展开实例验证. 试验结果表明,基于可扩展多目标蚁群算法的土地利用优化配置模型能够灵活地适应不同的多目标体系,对区域内的土地利用布局进行合理配置,提高区域内的土地利用率,促进土地的可持续发展.当前的模型将土地利用类型分为5类比较简单,因此下一步研究要细化模型的土地利用类型,提供更精细的土地利用分类,提高模型的现实可靠性;另外,土地利用优化配置目标非常复杂,且相互之间并非线性关系,因此未来须对可扩展多目标体系中各个目标的权重策略进行深入研究,加强可扩展多目标体系对土地利用优化配置的指导作用. [1] 高小永.基于多目标蚁群算法的土地利用优化配置[D].武汉: 武汉大学,2010. GAO X Y.OptimizingLandUseAllocationBasedonMulti-ObjectiveAntColonyAlgorithm[D]. Wuhan: Wuhan University,2010. [2] 刘彦随,陈百明.中国可持续发展问题与土地利用/覆被变化研究[J].地理研究, 2002, 21(3): 324-330. LIU Y S, CHEN B M. The study framework of land use / cover change based on sustainable development in China[J].GeographicalResearch, 2002, 21(3): 324-330. [3] 张鸿辉,曾永年,谭荣,等.多智能体区域土地利用优化配置模型及其应用[J].地理学报, 2011, 66(7): 972-984. ZHANG H H, ZENG Y N, TAN R, et al. A model for regional land use optimization allocation based on multi-agent system and its application[J].ACTAGeographicaSinica, 2011, 66(7): 972-984. [4] 覃刚力,杨家本. 自适应调整信息素的蚁群算法[J].信息与控制,2002, 31(3): 198-201. QIN G L, YANG J B. An improved ant colony algorithm based on adaptively adjusting pheromone[J].InformationandControl, 2002, 31(3): 198-201. [5] COLORNI A, DORIGO M, MANIEZZO V. Distributed optimization by ant colonies[C]//Ecal91-EuropeanConferenceonArtificialLife. Paris: Elsevier Publishing, 1991: 134-142. [6] DORIGO M. Ant colonies for the traveling salesman problem[J].Biosystems, 1997, 43(2): 73-81. [7] 刘建华,杨建国,刘华平,等.基于势场蚁群算法的移动机器人全局路径规划方法[J].农业机械学报,2015, 46(9): 18-27. LIU J H, YANG J G, LIU H P, et al. Robot global path planning based on ant colony optimization with artificial potential field[J].TransactionsoftheChineseSocietyforAgriculturalMachinery, 2015, 46(9): 18-27. [8] 李倩,张惠珍,CESAR B.带投资约束P-中位问题的混合蚁群算法[J].计算机应用研究,2017, 33(6): 1-7. LI Q, ZHANG H Z, CESAR B. Hybrid ant colony algorithm for capacitated p-median problem with investment[J].ApplicationResearchofComputers, 2017, 33(6): 1-7. [9] 高晋凯,侯文,杨冰倩,等.基于蚁群算法的模糊C均值聚类的改进研究[J].现代雷达,2016, 38(11): 30-34, 39. GAO J K , HOU W, YANG B Q, et al. Improved fuzzy C-means clustering based on ant colony algorithm[J].ModernRadar, 2016, 38(11): 30-34, 39. [10] DAS B, SINGH A, PANDA S N, et al. Optimal land and water resources allocation policies for sustainable irrigated agriculture[J].LandUsePolicy, 2015, 42(42): 527-537. [11] 徐磊,董捷,张安录.湖北省土地利用减碳增效系统仿真及结构优化研究[J].长江流域资源与环境,2016, 25(10): 1528-1536. XU L, DONG J, ZHANG A L. Study on simulation and structure optimization of land use carbon reduction and efficiency improvement system of Hubei province[J].ResourcesandEnvironmentintheYangtzeBasin, 2016, 25(10): 1528-1536. [12] 黄海.基于改进粒子群算法的低碳型土地利用结构优化——以重庆市为例[J].土壤通报,2014, 45(2): 303-306. HUANG H. Optimization of low-carbon land use structure based on improved particle swarm optimization algorithm: A case study in Chongqing municipality[J].ChineseJournalofSoilScience, 2014, 45(2): 303-306. [13] CHEN P Y, TUNG C P, LIN W C, et al. Spatial optimization procedure for land-use arrangement in a community based on a human comfort perspective[J].PaddyandWaterEnvironment, 2016, 14(1): 71-83. [14] 袁满,刘耀林.基于多智能体遗传算法的土地利用优化配置[J].农业工程学报,2014, 30(1): 191-199. YUAN M, LIU Y L. Land use optimization allocation based on multi-agent genetic algorithm[J].TransactionsoftheChineseSocietyofAgriculturalEngineering, 2014, 30(1): 191-199. [15] LIU Y, LIU Y, PENG J, et al. Psola: A heuristic land-use allocation model using patch-level operations and knowledge-informed rules[J].PlosOne, 2016, 11(6): e0157728. [16] 刘艳芳.经济地理学:原理、方法与应用[M]. 北京: 科学出版社,2006. LIU Y F.EconomicGeography:Principles,MethodsandApplications[M]. Beijing: Science Press,2006. [17] GOSS S, ARON S, DENEUBOURG J L, et al. Self-organized shortcuts in the Argentine ant[J].TheScienceofNature, 1989, 76(12): 579-581. [18] BIN A, MA S F, SHUO W. Land-use zoning in fast developing coastal area with ACO model for scenario decision-making[J].GeospatialInformation, 2015, 18(1): 43-55. [19] 李颖,黄贤金,甄峰. 江苏省区域不同土地利用方式的碳排放效应分析[J].农业工程学报,2008, 24(S2): 102-107. LI Y, HUANG X J, ZHEN F. Effects of land use patterns on carbon emission in Jiangsu province[J].TransactionsoftheChineseSocietyofAgriculturalEngineering, 2008, 24(S2): 102-107. [20] 周婷婷,毛春梅.我国土地利用与碳排放的关系研究[J].安徽农业科学,2012, 40(2): 1175-1177. ZHOU T T, MAO C M. Research on the relation between land use and carbon emissions in China[J].JournalofAnhuiAgriculturalSciences, 2012, 40(2): 1175-1177. [21] 谢高地,甄霖,鲁春霞,等.一个基于专家知识的生态系统服务价值化方法[J].自然资源学报,2008, 23(5): 911-919. XIE G D, ZHEN L, LU C X, et al. Expert knowledge based valuation method of ecosystem services in China[J].JournalofNaturalResources, 2008, 23(5): 911-919. MO Zhiliang1,2, DU Zhenhong1,2, ZHANG Feng1,2, LIU Renyi1,2 (1.ZhejiangProvincialKeyLabofGIS,ZhejiangUniversity,Hangzhou310028,China; 2.DepartmentofGeographicInformationScience,ZhejiangUniversity,Hangzhou310027,China) Landuseoptimizingallocationbasedonextensiblemulti-objectiveantcolonyalgorithm.Journal of Zhejiang University (Science Edition),2017, 44(6): 649-659, 674 The traditional land use optimizing allocation model can’t flexibly response to the changing optimizing requirements under the realities, and can’t achieve the optimization of land use in spatial layout. This paper abstracts modeling based on the common optimizing targets, and establishes an extensible multi-objective system combining with the ant colony algorithm. Finally, a land use optimizing allocation model based on extensible multi-objective ant colony algorithm is constructed, making the land use optimizing allocation more flexible under the direction of different multi-objective systems, realizing the unification of land use optimizing allocation in structure and spatial layout, and providing a more practical reference for land use planning. The Xiaoshan district of Hangzhou is an area of good economic, social and ecological environment, which makes it a good choice of our study area to verify the model. The experimental results show that the model can reasonably allocate the land use layout of the study area under the guidance of multi-objective system, promote the sustainable development of regional land use, and give different optimization schemes for different multi-objective systems. land use optimizing allocation; ant colony algorithm; extensible multi-objective system 2017-08-10. 国家自然科学基金资助项目(41471313,41101356);浙江省科技攻关计划项目(2013C33051);国家海洋公益性行业科研专项(201505003-6,201305012);国家科技基础性工作专项(2012FY112300);中央高校基本科研业务费专项资金资助项目(2016XZZX004-02). 莫致良(1990—),ORCID: http: //orcid.org/0000-0001-7571-3425,男,硕士,主要从事国土资源地理信息系统基础研究. *通信作者,ORCID: http: //orcid.org/0000-0001-9449-0415,E-mail: duzhenhong@zju.edu.cn. 10.3785/j.issn.1008-9497.2017.06.003 P 208 A 1008-9497(2017)06-649-112 实例验证与结果分析



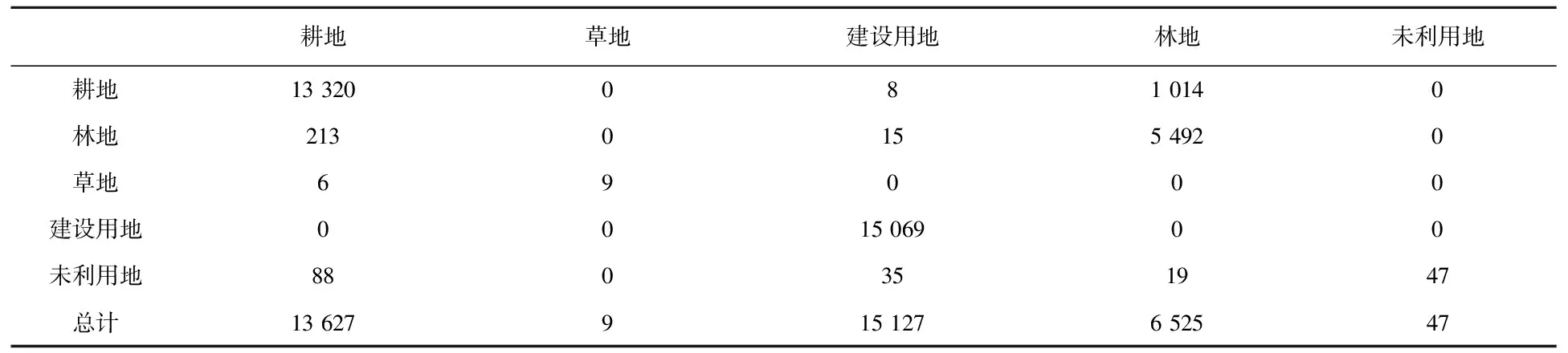
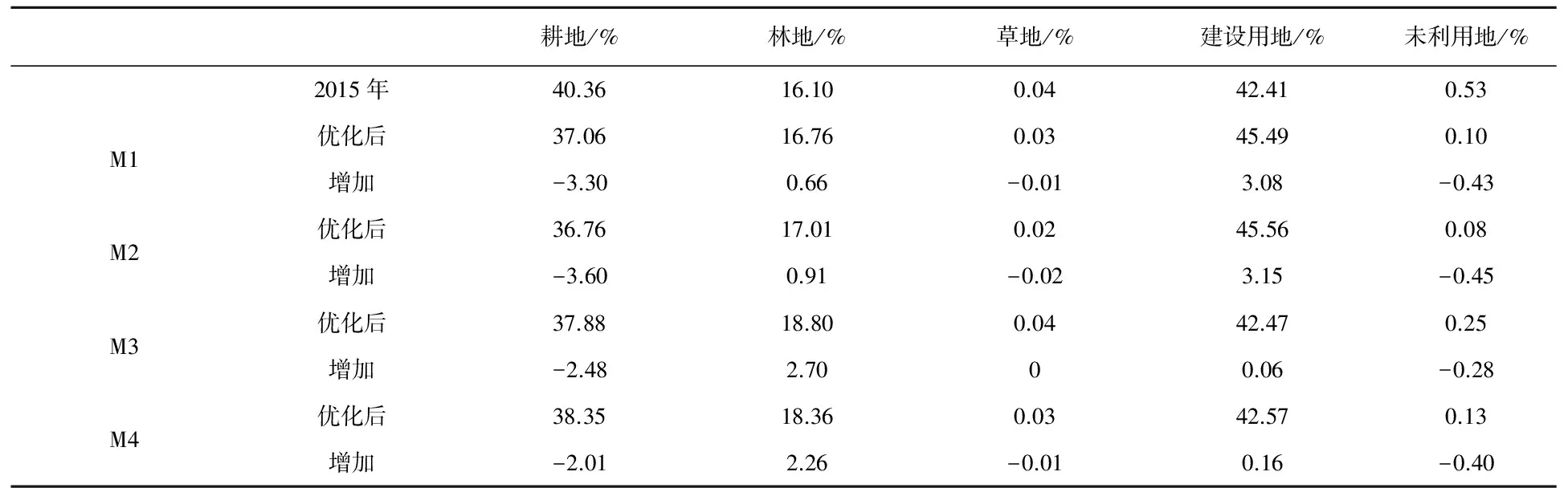

3 结论与讨论

