无扰载荷航天器相对运动动力学建模

孔宪仁，武 晨，刘 源，李海勤

(哈尔滨工业大学卫星技术研究所, 哈尔滨 150080)

无扰载荷航天器相对运动动力学建模

孔宪仁，武 晨，刘 源，李海勤

(哈尔滨工业大学卫星技术研究所, 哈尔滨 150080)

为满足无扰载荷(DFP)航天器中非接触式作动器对有效载荷模块(PM)与支持模块(SM)之间相对运动的要求，本文建立了PM与SM之间的六自由度相对运动动力学模型。考虑立方构型DFP接口，分析了作用于PM与SM的力和力矩。考虑DFP航天器相对运动控制的特殊性，建立了SM相对PM的相对姿态动力学模型和PM相对SM的相对平动动力学模型，然后采用比例微分(PD)控制方法设计了DFP航天器的控制系统。数值仿真结果表明，定向状态或姿态机动过程PM与SM六自由度相对运动均满足非接触式作动器作用范围的要求，既可保证PM与SM无机械接触，又可实现对PM精确定向和姿态机动，说明六自由度相对运动动力学建模对研究DFP航天器具有重要意义。

无扰载荷(DFP)航天器；超高指向精度；立方构型DFP接口；相对运动动力学模型

0 引 言

随着人类对宇宙的不断探索，对航天器有效载荷精确定向与稳定性提出越来越严苛的要求。对于超高精度航天器，振源部件产生的高频微振动是必须考虑的关键影响因素之一，文献[1]全面概述了目前对高频微振动主要的隔振方法，并评述了各自的局限性。为了从根本上解决有效载荷的隔振问题，Pedreiro[2]提出了一种新型航天器结构——无扰载荷(Disturbance-free-payload，DFP)结构。DFP航天器将传统的航天器拆分为有效载荷模块(Payload-module，PM)、支持模块(Support-module，SM)和DFP接口。具有高精度要求的有效载荷部件安装于PM上，如空间相机、光学敏感器以及空间激光器等，而产生振动的部件及其他附件安装于SM上，如反作用飞轮、推力器、柔性帆板和计算机等。DFP接口由非接触式作动器(如音圈电机)和非接触式敏感器(如电感式传感器)组成，主要用于实现PM的六自由度控制和非接触式连接PM与SM。因此可在对PM的六自由度控制的同时保证PM与SM无机械接触。由于DFP航天器中PM与SM之间无机械接触，理论上可完全消除航天器振源部件对高精度有效载荷性能的影响。

文献[2]详细介绍了DFP航天器，并以DFP结构的下一代空间望远镜(Next generation space telescope,NGST)[3]分析了DFP结构对PM的隔振性能。Pedreiro等[4]建立了DFP结构NGST的二维物理试验模型，通过试验展示了DFP结构对PM的精确定向性能以及快速机动性能。Gonzales等[5]改进了文献[4]中的试验设备，可使DFP航天器获得更高的隔振性能。Pedreiro等[6]还提出将DFP结构应用于敏捷航天器中，并验证了其可行性。Trankle等[7]建立了DFP航天器的线性和非线性仿真模型，分析了隔振性能和机动性能。Xu等[8]建立了接口动力学模型，并设计了H∞鲁棒姿态控制系统，而没有研究PM与SM之间的相对平动。庞岩等[9]建立了带有柔性连接缆线的DFP航天器的动力学模型，分析了柔性连接缆线对PM超高精度的影响。

综上所述，目前对DFP航天器的研究较多集中于性能展示，而在其相对运动动力学模型方面有所欠缺。DFP航天器中PM与SM之间的相对运动不同于航天器之间的相对运动，航天器之间的相对运动控制只需控制随从航天器接近主航天器，而DFP航天器中需要通过非接触式作动器和SM上的常规执行机构协同控制PM与SM的相对位姿，因此其相对运动动力学模型具有一定的特殊性。对航天器之间的相对运动动力学建模已有大量研究[10-18]，但当两个航天器相距较远时其相对运动动力学模型并不适用于DFP航天器。

本文针对具有六杆立方体构型接口的DFP航天器，分析了DFP接口作用于PM与SM的力与力矩，推导获得了PM相对于SM的相对平动动力学模型和SM相对于PM的相对姿态动力学模型。设计了DFP航天器的PD控制系统，并通过数值仿真分析了PM与SM的相对位姿，以及DFP结构的隔振性能和机动能力。

1 DFP接口力学分析

1.1DFP接口概述

典型的DFP接口构型有六杆平台构型和八杆磁悬浮构型[19]，本文采用六杆立方构型[20]DFP接口，如图1所示。Li(i=1,2,3,4,5,6)表示DFP接口的支杆i;s12，s34和s56为支杆与SM平台的连接点，p61，p23和p45为支杆与PM平台的连接点，PM和SM分别安装于PM平台和SM平台上。DFP接口中的每个支杆上安装一组非接触式作动器与非接触式敏感器。

建立DFP接口作用力模型需明确若干坐标系：轨道坐标系O-XYZ，PM平台坐标系P-XPYPZP，SM平台坐标系S-XSYSZS，PM体坐标系BP-XPBYPBZPB和SM体坐标系BS-XSBYSBZSB，如图2所示。轨道坐标系O-XYZ原点位于SM质心处，作为PM和SM运动以及二者相对运动的参考坐标系，平台坐标系原点位于平台质心处，体坐标系原点分别位于PM和SM质心处。PM和SM分别与PM平台和SM平台刚性连接，因此坐标系BP-XPBYPBZPB和BS-XSBYSBZSB分别与坐标系P-XPYPZP和S-XSYSZS相对静止。

1.2力学分析

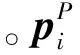
(1)

(2)

非接触式作动器为电磁式作动器，由铁磁体与通电线圈组成，且分别通过刚性杆与PM平台和SM平台连接，连接点分别为pi和si，如图3所示。则在连接点pi和si处非接触式作动器作用于PM和SM的作用力分别为：

(3)

作用力fi引起的作用于PM和SM的力矩分别为：

(4)

考虑DFP接口中的6个非接触式作动器的输出力，作用于PM与SM上的作用力分别为：

(5)

作用于PM与SM上的力矩分别为：

(6)

2 相对运动动力学模型

DFP航天器的动力学模型包括PM姿态动力学模型和PM与SM之间的六自由度相对运动动力学模型。PM的姿态动力学模型与一般航天器的姿态动力学模型类似，本文不作赘述。本节主要建立PM与SM之间的六自由度相对运动动力学模型，包括PM相对SM的相对平动动力学模型和SM相对PM的相对姿态动力学模型。

2.1PM姿态动力学模型

DFP结构中，PM姿态由DFP接口中的非接触式作动器控制，则PM所受控制力矩即为TPV。设PM的三轴姿态角分别为φP，θP和ψP，干扰力矩为TPd=[TPdx,TPdy,TPdz]T，则其姿态动力学模型为：

(7)

式中：TPVx，TPVy和TPVz分别为TPV的分量；ω0为轨道角速度大小；IPx，IPy和IPz为PM的转动惯量。

2.2相对平动动力学模型

设PM与SM在惯性系下的位置矢量分别为RP和RS，根据牛顿定律可得PM与SM的运动方程为：

(8)

式中：aPd和aSd分别为作用在PM和SM上的干扰加速度,aP和aS分别为作用在PM和SM上的控制加速度，在轨道坐标系下可表示为：

(9)

式中：mP和mS分别为PM和SM的质量。

惯性系下PM质心相对于SM质心的相对位置矢量为：

ρI=RP-RS

(10)

式(10)求二次导数，并考虑DFP结构航天器中PM与SM在同一轨道且相距较近，即RP≈RS，可得质心相对加速度为：

(11)

设轨道坐标系下PM质心相对于SM质心的相对位置矢量可表示为ρ，则质心相对加速度可表示为：

(12)

将式(11)代入式(12)，可得：

(13)

其中,ω0为惯性坐标系下的轨道角速度，表示为

ω0=[0, 0,ω0]T

(14)

将式(9)代入式(13)可得PM相对SM的相对平动动力学模型为：

(15)

2.3相对姿态动力学模型

设SM与PM的角速度在各自体坐标系下的表示分别为ωS与ωP，则SM相对于PM的角速度为：

(16)

对式(16)求导可得：

(17)

(18)

PM与SM的姿态动力学方程分别为：

(19)

(20)

式中：IP与IS分别为PM与SM的转动惯量矩阵；TP与TS分别为PM与SM受到的力矩，TP包括DFP接口对PM的控制力矩TPV和PM所受干扰力矩TPd，TS包括SM上飞轮或推力器对SM的控制力矩TSc，DFP接口对SM的作用力矩TSV和SM所受干扰力矩TSd，即：

TP=TPV+TPd，TS=TSc+TSV+TSd

整理式(18)～式(20)可得：

(21)

将式(16)代入式(21)，则SM相对PM的相对姿态动力学模型为：

(22)

3 控制系统设计

DFP航天器控制系统结构[2]如图4所示。对DFP航天器的控制系统包括三个控制回路：PM的姿态控制，PM相对于SM的相对平动控制，SM相对于PM的相对姿态控制。本节采用PD控制方式分别设计了三个控制回路的控制律。

3.1PM姿态控制律

uPAC=KPD(Ω0-ΩP)+KPP(Θ0-ΘP)

(23)

式中：uPAC为PM姿态控制器输出,KPD和KPP分别为控制器比例和微分系数,Θ0和Ω0为期望姿态角与姿态角速度,ΘP和ΩP为PM姿态角与姿态角速度，分别为：

3.2相对姿态控制律

uRAC=KSD(ΩP-ΩS)+KSP(ΘP-ΘS)

(24)

式中：uRAC为相对姿态控制器输出,KSD和KSP分别为控制器比例和微分系数,ΘS和ΩS为SM姿态角与姿态角速度，分别为：

3.3相对位置控制律

(25)

4 数值仿真

本节数值仿真了DFP航天器定向和姿态机动两种运行状态，分析运行过程中PM与SM之间的相对姿态与位置。DFP航天器结构参数如表1所示，控制系统控制律如表2所示。

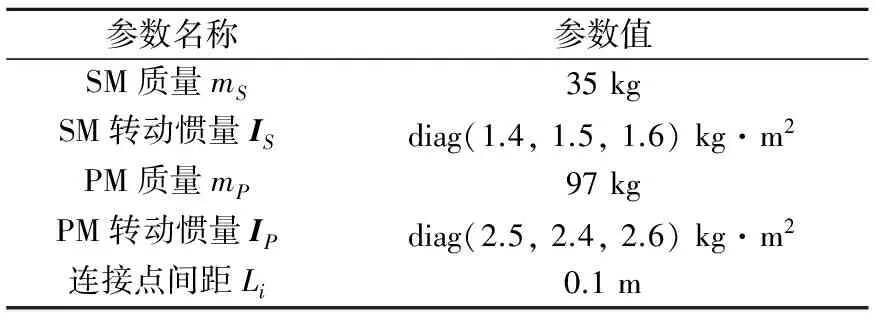
表1 DFP航天器结构参数Table 1 Structure parameters of DFP spacecraft

表2 控制系统参数Table 2 Parameters of the control system

数值仿真考虑了SM上飞轮动静不平衡引起的振动干扰力矩，设飞轮三正交安装，且飞轮参数相同，则干扰力矩数学模型如式(26)[22]所示：

(26)

式中：Ck为动静不平衡系数；ωx，ωy和ωz分别为三个方向上飞轮的转速；K为谐波数；hk为第k个谐波频率与飞轮转速之比；TID x，TID y和TID z分别为振动干扰力矩，模型参数如表3所示。由式(26)可知，振动干扰力矩与飞轮转速有关，具有较宽的振动频率范围。

表3 干扰力矩数学模型参数Table 3 Parameters of the disturbance torque

设非接触式作动器中铁磁体与通电线圈之间的作用范围小于5 mm，即铁磁体与通电线圈之间的距离超过5 mm非接触式作动器将不能正常工作。

4.1定向仿真结果

图5和图6分别为定向状态下PM和SM的姿态角曲线。由图5～6可知，存在飞轮动静不平衡的情况下，SM的指向精度约为5.137×10-2°，而PM的指向精度可达到4.873×10-5°，高于SM指向精度约3个数量级，说明飞轮动静不平衡不影响PM的指向精度，间接说明PM与SM之间通过非接触式作动器连接实现了无机械接触，且在定向过程中，PM与SM之间的相对运动控制可保证PM与SM保持安全距离无碰撞。

图7和图8分别为PM相对于SM的位置曲线和SM相对于PM的姿态曲线。由图7～8可知，PM相对于SM的位置保持在(0, 0, 1.2577) m左右，偏差不超过±1.5 mm，SM相对于PM的三轴姿态均保持0 rad左右，偏差不超过0.0015 rad。根据位姿偏差可计算获得对应连接点pi与si的间距Li，连接点分别与非接触式作动器中的铁磁体和通电线圈通过刚性杆连接，因此连接点间距可代表铁磁体和通电线圈的间距。图9所示为连接点间距Li，由图9可知，连接点间距均保持在0.1 m左右，且偏差在±1 mm范围内，说明非接触式作动器中铁磁体与通电线圈间距变化最大为±1 mm，满足非接触式作动器的正常工作要求。

4.2机动仿真结果

从图10可以看出，在50 s时PM 根据指令历时167 s俯仰轴姿态机动0.7 rad，SM可同步机动0.7 rad，说明DFP结构可完成航天器的姿态机动。图11表示姿态机动过程中连接点pi与si间距Li。由图11可知，间距保持在0.1 m左右，且最大偏差为±3 mm，虽大于定向过程中的偏差范围，但仍小于非接触式作动器中铁磁体与通电线圈之间的作用范围，满足非接触式作动器的正常工作要求。

5 结 论

本文针对DFP航天器，分析了六杆立方构型DFP接口中非接触式作动器对PM与SM的作用力和力矩，建立了PM与SM之间的六自由度相对运动动力学模型，基于PD控制方法设计了DFP航天器的控制系统。仿真结果表明，无论定向状态还是机动过程，PM与SM之间的相对位姿均可满足非接触式作动器的正常工作要求，在保证PM与SM无机械接触的同时实现PM的姿态控制和PM相对SM的位置控制，说明DFP航天器中相对运动动力学建模对深入研究DFP航天器具有重要意义。此外，验证了DFP航天器对有效载荷具有优越的隔振性能以及姿态机动能力。

[1] Liu C, Jing X, Daley S, et al.Recent advances in micro-vibration isolation[J]. Mechanical Systems and Signal Processing, 2015, 56: 55-80.

[2] Pedreiro N. Spacecraft architecture for disturbance-free payload[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(5): 794-804.

[3] Bely P Y,Perrygo C, Burg R. NGST yardstick mission[C]. The 34th Liege International Astrophysics Colloquium, Liège, Belgium, June 15-18,1998.

[4] Pedreiro N, Carrier A,Lorell K, et al. Disturbance-free payload concept demonstration[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, Monterey, USA, August 5-8, 2002.

[5] Gonzales M, Pedreiro N, Brookes K, et al. Unprecedented vibration isolation demonstration using the disturbance-free payload concept[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit， Providence, USA, August 16-19, 2004.

[6] Pedreiro N, Gonzales M, Foster B, et al. Agile disturbance free payload[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, USA, August 15-18, 2005.

[7] Trankle T, Pedreiro N, Andersen G. Disturbance free payload flight system analysis and simulation methods[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, USA, August 15-18, 2005.

[8] Xu Y F, Liao H, Liu L, et al. Modeling and robust H-infinite control of a novel non-contact ultra-quiet Stewart spacecraft[J]. Acta Astronautica, 2015, 107: 274-289.

[9] 庞岩, 李静, 刘磊. 柔性线缆连接的分离式卫星动力学建模[J]. 宇航学报, 2017, 38(1): 1-9.[Pang Yan, Li Jing, Liu Lei. Dynamics modeling of the separated satellite with flexible cable[J]. Journal of Astronautic, 2017, 38(1): 1-9.]

[10] Wang J, Liang H, Sun Z, et al. Finite-time control for spacecraft formation with dual-number-based description[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(3): 950-962.

[11] Condurache D, Burlacu A. On six-dof relative orbital motion parametrization using rigid bases of dual vectors[J]. Advances in the Astronautical Sciences, 2013, 150: 2293-2312.

[12] Wang J Y, Liang H Z, Sun Z W, et al. Relative motioncoupled control based on dual quaternion[J]. Aerospace Science and Technology, 2013, 25(1): 102-113.

[13] Segal S,Gurfil P, Shahid K. In-orbit tracking of resident space objects: a comparison of monocular and stereoscopic vision[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(1): 676-688.

[14] Chen Y,Rong S, Li S, et al. Adaptive pose tracking control for on-orbit tumbling target spacecraft[C]. The Fifth Instrumentation and Measurement, Computer, Communication and Control (IMCCC), Qinhuangdao, China, September 18-20, 2015.

[15] Filipe N,Tsiotras P. Adaptive position and attitude-tracking controller for satellite proximity operations using dual quaternions[J]. Journal of Guidance, Control, and Dynamics, 2014, 38(4): 566-577.

[16] Chen B,Geng Y. Super twisting controller for on-orbit servicing to non-cooperative target[J]. Chinese Journal of Aeronautics, 2015, 28(1): 285-293.

[17] Deng Y, Wang Z.Modeling and control for spacecraft relative pose motion by using twister representation[J]. Journal of Guidance, Control, and Dynamics, 2015, 39(5): 1147-1154.

[18] Lee D,Vukovich G. Kinematically coupled spacecraft relative motion without attitude synchronization assumption[J]. Aerospace Science and Technology, 2015, 45: 316-323.

[19] 张伟, 赵艳彬, 廖鹤, 等. 动静隔离, 主从协同控制双超卫星平台设计[J]. 上海航天, 2014, 31(5): 7-11.[Zhang Wei, Zhao Yan-bin, Liao He, et al. Design of an active-quiet isolated and master-slave coordination controlled dual-super satellite platform[J]. Aerospace Shanghai, 2014, 31(5):7-11.]

[20] Geng Z J, Haynes L S. Six degree-of-freedom active vibration control using the Stewart platforms[J]. IEEE Transactions on Control Systems Technology, 1994, 2(1): 45-53.

[21] Lee D, Bang H, Butcher E A, et al.Kinematically coupled relative spacecraft motion control using the state-dependent Riccati equation method[J]. Journal of Aerospace Engineering, 2014, 28(4).

[22] Masterson R A. Development and validation of empirical and analytical reaction wheel disturbance models[D]. Cambridge: Massachusetts Institute of Technology, 1999.

DynamicModelingofRelativeMotionforDisturbance-Free-PayloadSpacecraft

KONG Xian-ren, WU Chen, LIU Yuan, LI Hai-qin

(Research Center of Satellite Technology, Harbin Institute of Technology, Harbin 150080, China)

In the disturbance-free-payload (DFP) spacecraft, the relative motion between the payload-module (PM) and support-module (SM) should be researched to meet the requirements of the non-contact actuators. In this paper, the six-degrees-of-freedom relative dynamics model between the PM and SM is established. Focusing on the DFP spacecraft with a hexapod cubic DFP interface, the forces and torques acting on the PM and SM are analyzed. Then, the rotational dynamic model of the SM relative to the PM and the translational dynamics model of the PM relative to the SM are established considering the characteristics of the relative motion between the PM and SM. Furthermore, the control system of the DFP spacecraft is designed based on the proportional differential (PD) control. The simulation results show that the relative motion of the DFP spacecraft can satisfy the requirement of the non-contact actuators, whether it is pointing or maneuvering. This illustrates that the non-contact actuators can separate the PM and SM and control the PM simultaneously, and reveals the significance of the dynamic modeling of the relative motion for investigating the DFP spacecraft.

Disturbance-free-payload spacecraft (DFP); Ultra-high pointing accuracy; Cubic DFP interface; Dynamic modeling of relative motion

V421.4

A

1000-1328(2017)11- 1139- 08

10.3873/j.issn.1000- 1328.2017.11.001

2017- 06- 05;

2017- 09- 14

国家自然科学基金(51375109)

孔宪仁(1966-)，男，教授，博士生导师，主要从事振动控制，热控系统方面的研究。

通讯地址：黑龙江省哈尔滨市南岗区一匡街2号哈尔滨工业大学科学园B3栋(150080)

电话：(0451)86413300-8406

E-mail: kongxr@hit.edu.cn

武晨(1991-)，男，博士生，主要从事航天器振动控制方法方面的研究。本文通信作者。

通信地址：黑龙江省哈尔滨市南岗区一匡街2号哈尔滨工业大学科学园B3栋(150080)

电话：18800427014

E-mail: 14B918044@hit.edu.cn