突破计数单位学习困难的教学思考

梁洪超

[摘 要]在平时的教学和听课活动中發现，学生在学习整数、分数、小数的计数单位时都存在着较大的困难，而且大多数教师对计数单位的理解也存在偏差。通过深入挖掘教材对“10以内数的认识”中长方形背景框的使用，依托计数单位来衔接整数、小数和分数体系之间的联系，让学生在计数单位的拓展和累加中完成数的认识的学习，为学生的计算打下坚实的基础。

[关键词]计数单位；10以内的数；主体地位

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2017）32-0020-03

【重要地位】

数的认识的核心是对“位值原则”的理解，而“位值原则”可以理解为计数单位和进位法则的高度统一。正是计数单位的出现，才使人们实现了用0～9这10个数字来表示无穷无尽的数的可能。因此，从这个角度来看，计数单位是组成数的基石，在数的认识中有着不可替代的地位。

新课改后，计算教学的总课时数和习题数量都较以前大幅度减少，学生的计算能力也随之减弱。要改变这一现状，首先要求学生对算理有一定的理解，而理解算理又必须对计数单位有一定的理解，理解计数单位则要从数的认识的学习中实现。

目前，计数单位的教学到底处于一个什么样的状态呢？

【现象扫视】

现象一：学生学习小数的计数单位时感觉很难。

2010年春，我有幸参与了县小数研修班“小数的意义”的“同课异构，一课多上”的研讨活动，三位上课教师的教学都别具匠心，各有千秋，然而在教学小数的计数单位时，却碰到了相同的困难：即使教师费尽九牛二虎之力对学生加以引导，学生却总是似懂非懂，学得十分吃力。在课后的交流讨论中，与会教师也都觉得对此没有有效的应对之法。

后来我在“千课万人”的听课活动中，看到唐彩斌老师在执教“小数的意义”时，从学生熟知的整数引入，以教师的不同身高为载体，层层引入、环环相扣，不禁令人眼前一亮。然而，他在教学小数计数单位时，也遇到了同样的问题。

现象二：在调查学生掌握计数单位的情况中发现，正确率不足五成。

随后我对本校五年级七个班，学号末位数为0或5的学生进行了一次问卷调查，结果发现学生对计数单位的掌握情况不容乐观。

如，题目：整数的计数单位有（ ）、（ ）、（ ）、（ ）……与它们相对应的数位分别是（ ）、（ ）、（ ）、（ ）……小数的计数单位有（ ）、（ ）、（ ）（ ）……与它们相对应的数位分别是（ ）、（ ）、（ ）、（ ）……

学生解答该题的正确率仅为53.90%，其中有近六成的学生是因为分不清数位和计数单位的概念而出错。

后来我对四年级的学生进行访谈，听说过“计数单位”这一词的学生竟不足两成。大多数学生认为计数单位和数位很难区分，学习计数单位也没有什么用处。由此可见，学习计数单位的困难并不仅存在于“小数的意义”这一节课中，学生对整数和分数的计数单位的学习也存在同样的困难。

【成因分析】

1.对教材缺乏深入的研读

对于学生学习计数单位困难这个现象，诸多教师都认为造成这些的原因是教材中计数单位概念出现的次数太少。分析整套人教版教材，在1～12册教材中，出现“计数单位”这一完整概念的总共只有6次：第一、二次分别出现在四年级下册第3页“亿以内数的认识”和第20页“十进制计数法”的整数数位顺序表中；第三、四次分别出现在四年级下册第51页“小数的意义”和第52页“小数的读法和写法”的小数数位顺序表中；第五、六次分别出现在五年级下册第62页“分数的意义”和第64页练习十一的第8题中。如此重要的内容，在教材中的“出镜率”显然太低。尤其是对整数的教学，直到教学了“个、十、百、千、万、十万、百万、千万、亿”这些计数单位，在整数的认识教学即将结束时，教材中才第一次出现“计数单位”这一完整概念。

2.过分强调生活情境，缺少计数单位的适时抽象

课改后，越来越多的教师认识到数学情境生活化的重要作用和意义，然而数学情境过分生活化，却导致许多数学知识抽象程度不够，为学生日后学习更深层次的数学知识留下隐患。如，四年级下册“小数的加法和减法”中的“5.72+1.3”，对于为什么要把7和3相加而不是2和3相加，有的学生是根据元、角、分的情境来理解，认为角和角对应相加，分和分对应相加；有的学生是根据长度单位来理解，认为分米和分米对应相加，厘米和厘米对应相加；很少有学生能从“计数单位”的角度上去理解算理。虽然前两者的理解都对，但无论从数学知识的抽象程度，还是对学习后续知识的影响上看，教师都应该将学生向后者的方向上引导。其中，对后者理解上的缺失也正好反映了学生在学习“计数单位”中存在的问题。

3.教师对计数单位的理解也十分模糊

在与许多教师的访谈中发现，大家对计数单位的认知和理解存在着很大的分歧。有些教师认为：5个5个地数，5就是计数单位；8个8个地数，8就是计数单位；一位小数最大的计数单位应该是0.5，因为2个0.5正好可以凑成一个更大的计数单位。有些教师认为，只有以10个、100个、1000个等进行数数的时候才能将其叫作计数单位，而5个5个地数时，5就不能称之为计数单位。我专门就这一问题向杭州新思维培训中心的姜荣富老师请教，才清楚：无论是几个几个地数，都不能称之为计数单位，只能叫作按群计数，只有在计数和计算时才会有计数单位的概念。真正的计数单位只有1，其他的计数单位都是人为创造的。也就是说，只有在位值制出现后才有计数单位一说。

综上，学生出现上述问题的原因包括：传统教学中只重视计数单位的知识讲授，使得学生对计数单位的学习只停留在数的组成和分解之中，没有经历计数单位从量变到质变的逐步累加过程，忽略了新计数单位学习的必要性，以及理解和体会它的重要作用。因此，教学的改进可以从以下这几方面入手。endprint

【改进方略】

1.加強教材的深入发掘，重视长方形背景框的使用

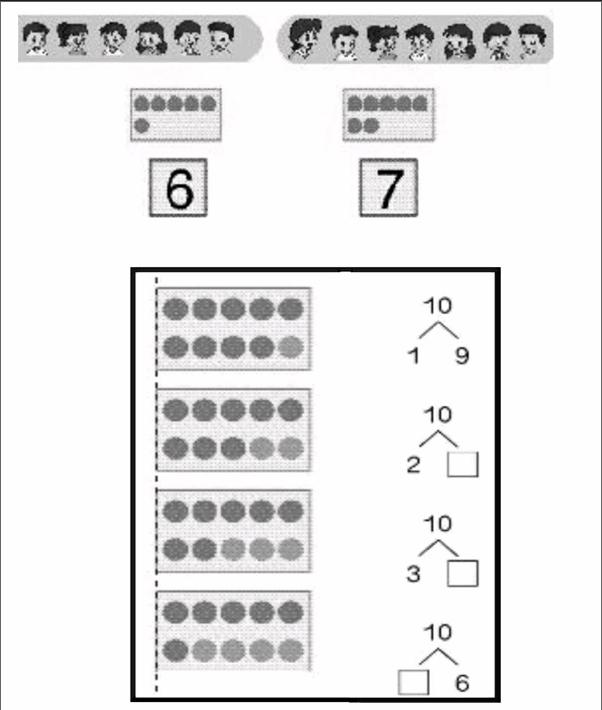
深入整理和研读教材中“10以内数的认识”的内容，不难发现，从“5以内数的认识”开始，到“10的认识”，教材中都配了长方形背景框中的点子图，这显然是对10作为计数单位的有意渗透。教师在教学时若能用好这个背景框，不但可以促进学生理解10作为计数单位的意义，对学生学习20以内数的进位加法和退位减法，并能够用凑整思想进行简算都大有帮助。

众所周知，20以内数的进位加法是一年级计算教学的难点，因此很多教师在教学“7加几的进位加法”时，常常会让学生背诵“看到7想到3，把几分成3和几……”的计算口诀，然而不少学困生对“看到7一定要想到3”表示难以理解，这是因为学生对“10”作为“计数单位”的理解不够深刻造成的。如果教师能在教学“6和7的认识”时，利用好点子图的背景框（渗透计数单位“10”）让学生思考“把这个长方形框摆满，还能再摆几个点子？你是怎么想的？”；在教学“10以内数的认识”时，对于10的分解和组成，结合点子图让学生画一画、想一想、做一做……学生就能获得对计数单位“10”更多的直观体验，给学习进位加法的算理打好基础。

2.在“10的认识”中突破“10”的局限性，让“10”成为新数认知的新起点

在教学“10的认识”时，“10”应该是本课教学的终点，大多数教师在教学中都会安排学生进行“把10根小棒捆成1捆，把10颗珠子串成1串”等操作活动，以此来加深学生对新的计数单位的理解。而这样的操作大都是“被操作”，学生并没有真正理解教师要求操作的目的。从“10作为计数单位”的角度来思考，“10”不该成为“10的认识”的教学终点，应该是学生认识新数的一个新起点。因为，从理论上讲，学生学了“10的认识”后再去数数时，应该就可以数到10个“十”。

因此，在以上操作活动的基础上，教师应带领学生再向前多走一步，让计数单位真正变得有用。

【教学片段】一年级上册“10的认识”

师（多媒体出示散乱的小方块，引导学生从1数到10；多媒体出示很多个散乱的小方块（100个），铺满整个屏幕）：共有几个小方块？

生1：太多了，数不清楚。

师：通过电脑操作，我们把原来分散的每10个“一”组合成了现在的1个1个的“十”。

师：现在我们再来数一数。

生2：一个“10”、两个“10”、三个“10”……一共有十个“10”。

师（小结）：“1个1个”散乱地数太费时了，我们可以把它们稍作整理，变成“10个10个”地数，就可以把原来数不清楚的小方块数得很清楚了。

在学习每一个新的计数单位时，都让学生经历这一幕，学生对计数单位的作用就能有更加深刻的体会了。

3.在小数和分数体系的认识和拓展中，让计数单位先行

张奠宙教授在2011年《小学数学教师》的第4期中就明确阐述了“小数有自己的概念系统，不能也不必依赖于对分数的理解”“小数的本质是位值计数法的拓展，而不是十分之几的表述”等观点。

【教学片段】小数的意义

师（出示一把没有刻度的尺子）：如果我用自然数1来表示这把尺子的长度，你觉得教室门的高大约可以用什么数字来表示？黑板的长呢？

生1：2、4。

师：这支毛笔的长度呢？能用几个1来表示？

生2：毛笔的长度还不到1。

师：也就是说现在用1作为计数单位太大了，那该怎么办？

生3：我们需要创造一个比1更小的计数单位。

师：有道理。那么我们把1平均分成几个小的计数单位比较好呢？

生4：平均分成10个比较好，因为整数也是满十进一。

师：你很会思考，整数是满十进一，这里就可以是“一分为十”。

师（多媒体演示：把一把尺子平均分成10份） ：这样我们就创造了一个比1更小的计数单位——0.1（十分之一），那接下来（取下自制尺子中的0.1，边演示边讲解）我们就可以0.1为单位进行计数和测量物品了。

师：数数看1里面一共分成了几个0.1呢？（板书：1里面有10个0.1）那么，现在毛笔的长度是几个0.1呢？3个0.1可以怎么表示？

生5：0.3。

师：空白部分有几个0.1，可以用什么分数来表示？

生6：7个0.7，表示为■。

师：没错，有了0.1这个计数单位以后，就可以方便我们数数了。我们一起来数一数。（教师带领学生一起从0.1数到1）

师：这个0.1是把1平均分成10份，每一份其实就是分数里的十分之一，所以我们也可以十分之一、十分之一地数。0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0、1.1……

【设计意图：两次数数，第一次以0.1为单位数，第二次以十分之一为单位数，从而帮助学生理解小数都是由0.1累加而成的，十分之几是由十分之一累加而成的，进一步强化了学生对计数单位的体验，有利于增强学生对小数意义的理解，与华罗庚先生“数，数也！”的见解相吻合。】

其实，无论整数、分数、小数，还是十进制、二进制、八进制等，都只是计数单位和进位法则上存在区别，在这些内容中，整数的十进制是学生学习课时最长，生活体验最为丰富的内容。因此，教师要抓住计数单位的改变这一主线，先拓展计数单位，再带领学生数计数单位的个数，最大限度地借助学生整数学习中的经验，依托计数单位让学生对小学阶段各数系的认识实现无缝对接，以此为后续的相关计数教学打好基础。

[ 参 考 文 献 ]

[1] 中华人民共和国教育部.全日制义务教育数学课程标准（修订稿）[S]. 北京：北京师范大学出版社，2010.

[2] 张奠宙. 谈小数教学[J]. 小学数学教师，2011（4）.

[3] 吴振亚. 关于计数单位的教学思考[J]. 小学教育教学，2011（1）.

（责编 童 夏）endprint