浅谈OFDM系统中基于导频的几种常用的信道估计算法

徐筱昕，贾亦真

（中国卫通集团有限公司，北京 100094）

浅谈OFDM系统中基于导频的几种常用的信道估计算法

徐筱昕，贾亦真

（中国卫通集团有限公司，北京 100094）

无线通信系统由于信道环境复杂，具有很大的随机性,误码率常常很高。能否获得详细的信道信息，从而改善接收端的误码率，是衡量一个无线通信系统性能的重要指标。本文针对正交频分复用（OFDM）系统中基于导频的信道估计技术，分析几种常用的信道估计算法，并使用MATLAB对模拟信道中的几种估计算法进行仿真比较。

信道估计；OFDM系统；最小二乘法；导频

1 引言

OFDM是一种多载波技术，它将信道分成若干份，保证每个子信道之间是相互正交的。传输的信号由串行转化为并行，再分别被调制到各个子信道上。这样的话，传输过程中各个子信道上的信号之间干扰减小，传输质量会得到提升。在接收端，通过同步和相干检测对传输的信号进行恢复，从而得到我们所需要的信息。

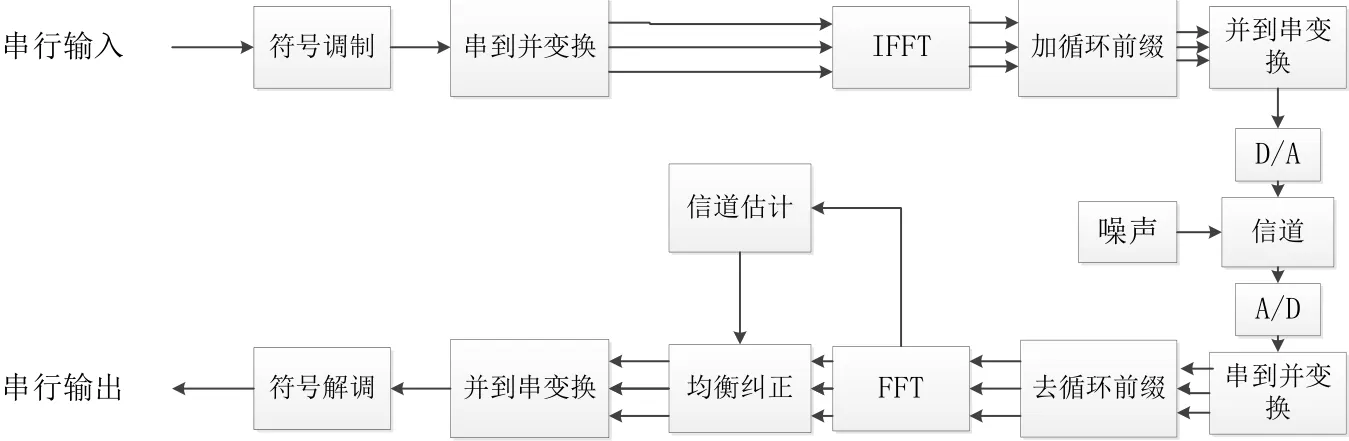
图1 OFDM系统实现框图

以上可以看出，采用OFDM技术需要用到相干检测。同时，面对多变的信道环境，我们需要一种方式能随时的跟踪信道变化。信道估计技术就是基于这样的考虑应运而生的。信道估计的结果不仅可以实时的反映当前信道的情况，成为可供我们参考的信道信息，同时还可以在信道均衡的问题上提供帮助，有利于提升信息传输的质量。因此，多年以来，信道估计技术始终是一个长盛不衰的研究热点。

2 信道估计技术研究现状

当下基于OFDM系统的信道估计方式主要可以分为三大类：第一种是利用导频序列对信道进行估计，第二种是盲信道估计以及半盲信道估计，第三种是利用将训练信号隐含在数据中一同传输的隐训练序列信道估计。

从复杂程度上来说，基于导频的信道估计方式是最简单的，但是这种方式会占用带宽资源。从更好的利用带宽的角度来说，它不算是一种好方法。这种方式的基本原理就是将导频按一定的规律和方式插入到发送的信号之中。导频信号与数据信号一同在信道中传输，在接收端通过提取出导频信号与原导频信号进行比对，再通过相应的内插方法得到所有数据点的信道信息，以实现对信道的估计。盲信道估计则是利用调制信号的一些固有特性以及通过判决反馈的方式对信道进行估计。半盲估计将盲估计和导频估计的一些特点进行融合，导频插入较少。虽然盲信道估计和半盲估计的频带利用率较高，但也有它们自己的应用局限性，需要长时间对数据进行观察，会出现相位模糊、收敛速度慢、误差传播等问题。

隐训练序列信道估计可以说是当下最受欢迎的信道估计方式。训练序列的符号和数据部分的符号叠加起来一同通过信道，接收端通过接收到的信号和训练序列符号不相关的特性，经由一定的算法就可以得到信道信息了。但是，这种估计方式的结果受到训练序列和发送数据相关性的影响比较大。两种信号的相关性越小，估计出来的效果就越好。

3 基于导频的信道估计方法

导频辅助的信道估计方法是在发送信号之前按照一定的插入方式将已知的数据插入我们所要传输的数据之中，插入位置分为块状、梳状、梅花状，插入域又可以选择时域或是频域，或者两个域都插入。然后将导频信号和信息数据一起传输通过信道，接收的时候，把这些收到的导频与原本传输的导频通过一定的算法联系起来，得到一个关系函数，我们就可以把这个函数作为信道的反映。最后，通过某种插值方式还原整个信道的数据，具体插值方式也要根据实际情况来选择。

导频插入间隔与插入图案有关，Nyquist抽样定理要求fs≥2fm，fm是发送信号最高的频率，fs这里代表采样的频率，只有满足这样的条件才能在收端完整还原出原来的信号。相应地，变换到时域上，也就是说导频插入的间隔不能大于2fm的倒数。为了更好的跟踪信道，导频间隔当然越小越好。但是，导频的插入本身就是一种对带宽资源的浪费，可以说是利用一部分有用的资源来估计信道，导频插入间隔过小是得不偿失的。

为了全面的反映信道信息，导频插入位置的安排也可简单分为3类。块状位置分布是在时域上间隔的插入导频。可以理解为导频被周期性的插入到OFDM符号的所有子载波中。这种估计方式的精度在平稳变化的信道条件下比较好，导频覆盖了所有频率，可以较好地应对频率选择性，不需要在频域插值。但是，缺点也比较明显，由于这种方式相当于是离散的采样，两个导频符号之间的信息就会有一定程度上的缺失。信道情况变化小的慢衰信道更适合采用这种方法。

梳状位置分布是取某些子载波固定的传输导频，其余子载波上传输数据。它在时域上连续，频域上间隔插导，正好和之前提到的块状相反。这种方式对频率的影响很敏感，但是跟踪信道变化的能力优于块状。梳状更适宜快衰信道，也就是那些随时间变化比较快的信道。

还有一种，就是学术上称为网状或是梅花状的位置插入方式，其实就是将上述的两种方式做一个混合，可以在一定程度上弥补前面两种方式各自的缺点，高速传输时估计效果更好。不过这种方式计算难度大，花费时间长。即便如此，这样的安排仍旧在实际应用中占有一定的地位，当实时性要求不高时，可以选择这种方式进行估计。

梳状和块状导频位置示意，可以参考图2，●代表导频，○代表数据。

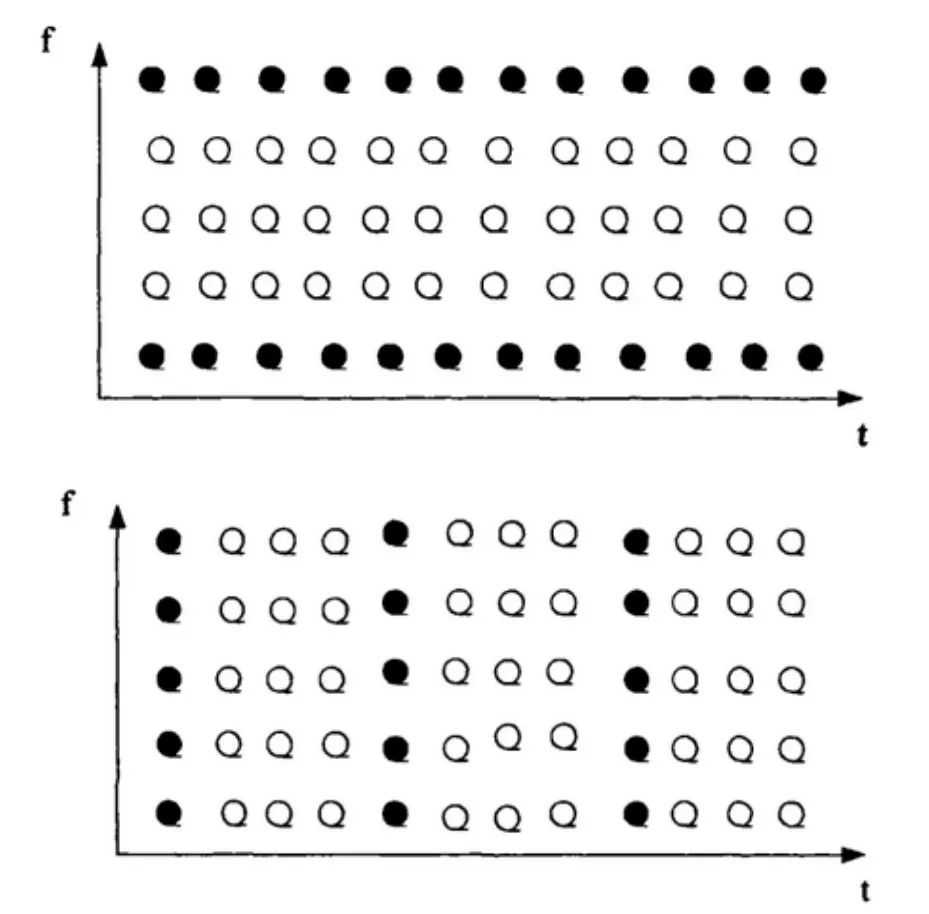
图2 梳状和块状导频位置示意图

4 常见的信道估计算法

4.1 LS算法

这是一种算法简单并且容易理解的估计算法，也是研究中最常用最基础的一种。背后的思想是以适应模型的方式来对信道进行测量，使实际值减去估计值的平方的总和是最小的。在块状导频安排中，导频在OFDM符号的全部子载波中都被插入了，LS估计的信道传递函数可以写成：

在梳状导频安排中，Np个导频信号Xp=(m),m=0,1,...,Np-1均匀的插入X(k)。经过调制，在第k个子载波的OFDM信号就可以表示为：

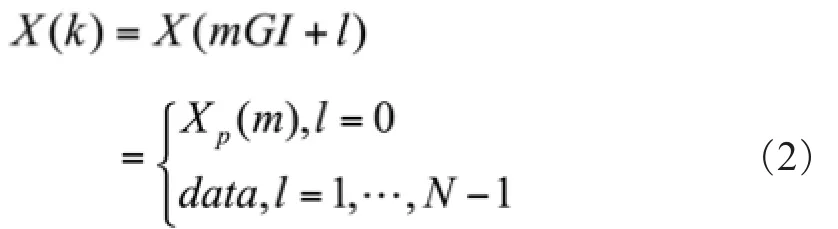
式中，GI=N/Np。假设把接收的导频信号矢量表达为下式：

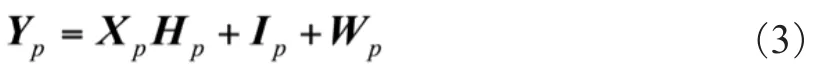
式中，

式中，Ip是信道间干扰（ICI）的矢量；Wp是导频子载波中的高斯白噪声。如果Ip和Wp假定被保护带除去，梳状导频安排中基于最小二乘（LS）准则的导频估计由下式给出：

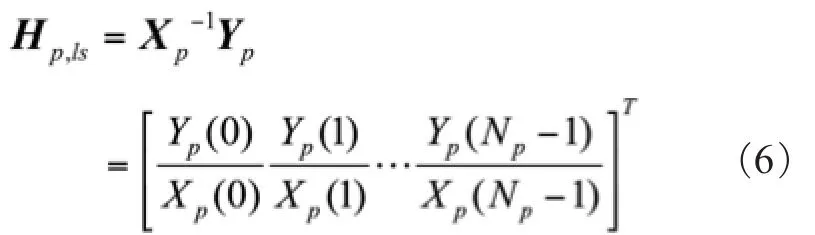
因为最后得到的整个的信道响应是以导频处的响应值作为参考，再在其间插值所得到的，所以OFDM系统的性能在基于梳状导频安排中通常高度依赖于导频信号估计的准确度。不过，这种算法把噪声影响也当作了信道响应来处理，没有考虑到ICI影响，所以效果并不是很理想。但是，由于简单易行，使用的还是很多。实际上，这种估计算法是基于数学的理论得来的，使实际和估计的误差平方最小，以下是（6）式的推导过程：

式中，右上角的H代表转置共轭；F是一个矩阵（N维的），把代入（7）式就可以得到（6）式了。

4.2 LMMSE算法

如果对估计精度的要求高些，LS可能就达不到了，所以可以采用这种使线性均方误差最小的方式，在平方和的基础上再进行平均。当信道满足随机性，符合高斯要求并且噪声特性独立的时候，信道的估计值可以用下式表示：

如果我们按照上面的（8）来计算的话，就会发现计算量非常的大，虽说估计效果有所改善，但是随着N的增加和求逆矩阵部分的计算，还是会把大量的时间浪费在计算上，最传统的MMSE方式就是这么做的。而我们所要说的LMMSE是在MMSE的基础上进行线性变换，是其中的一种特殊情况。

把4.1中的LS公式和MMSE结合一下得到：

然后，我们用近似量替换某些复杂量，把(XXH)-1换成。其他文献中对于这种近似的仿真表明，这种替换对于结果的影响很小，是可行的。如果每个信号在系统中的调制的概率相同的情况下，就会满足：

β在这里是由具体的调制方式所决定的，是个常数，比如本文仿真部分使用的是16QAM的技术，那么β=17/9，如果用的是QPSK那么β=1。

以上可以看出，好的估计效果也会带来实现难度的升高，所以严格意义上来说LMMSE的算法不够完美，不仅求逆复杂度高，还要事先得到一些统计特性。所以很多学者致力于研究如何将这种估计效果好的算法赋予更多的优点，比如降秩。

4.3 基于SVD的低秩LMMSE算法

对这种算法只做一个简单的介绍，它是在LMMSE算法上进化而来，利用给矩阵降秩的方式来减小复杂度的。式中，，U表示满秩酉阵（N）， 是RHH特征值分解（λ），按降序组成对角阵列，只取前r阶：

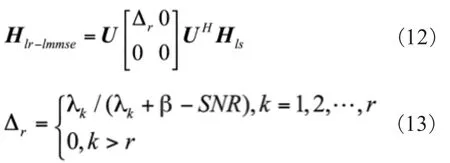
4.4 基于LS的DFT算法

这种算法不仅利用快速算法将计算过程大为简化，而且还可以人为的消除部分噪声的干扰。我们知道，信号在通过信道的时候对信道的响应通常只有一小段，而我们设计OFDM系统时加入的保护间隔又常远大于多径传输带来的影响时间，包括噪声在内的影响都被计算在LS的信道响应中。实际上，有很多能量小的点我们都可以把它当作是多余的部分，只考虑集中的几个能量大的点。

信号处理里面有种叫做泄漏的说法，虽然原理不同但是效果上跟这种拖尾多余的信道响应是类似的。如果我们有选择性的来选取响应点，将其他点的响应当作0来处理，一定程度上就能补偿原本LS中噪声的影响。可用图3来表示这个过程：（保证时域处理后的长度L不变）

图3 DFT算法过程

5 插值方法

在导频处的估计已知的情况下，就需要借助插值来对整个信道进行还原，最常用的就是线性插值。不过，所有的插值都离不开一个基本模式：

线性插值（Linear）就是把两个点连起来，然后把连线上的点作为要插入的点，这里的点就是指挨着的两个导频，满足均匀分布。不管是在频域还是时域都是如此，计算速度快，但是拟合度也稍差，斜率不是变化的所以线是折行的。

三次样条（Spline）插值是一种利用低次的多项式来模拟曲线变化的方法，它将整个曲线分成几段，用4个系数来拟定每一段变化。比如我们有7个导频，那么就有6段要插值，每一段都要解一个三次多项式，采用的公式为（i是段数）：

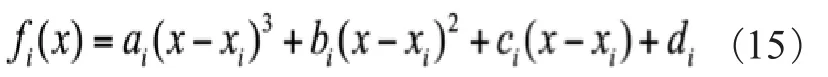
这种方式的要求比较高，曲线最为光滑，保证一、二阶导都连续，最大的缺点就是计算量很大，不均匀的分布会使结果异常。

除了上面两种方式之外，还有利用高数里的language公式N次多项式来插值的方法，两点之间可以间隔不等，计算起来比较麻烦。上述提及的各种插值的方式都是让相邻的两个参考点之间的连线能更接近真实曲线，只有这样我们才能把中间的取值作为我们估计时的插入值。虽然牺牲准确度可以换来过程的简化，但是要想获得更贴近真实的估计还是要用比较复杂的方法。

6 信道估计的MATLAB仿真与比较

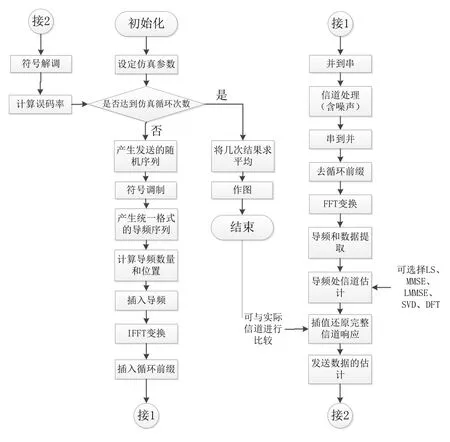
图4 仿真流程图

仿真条件设定如下：传输100个OFDM符号，循环前缀=16（大于最大时延），128路载波每符号，五径衰落信道加白噪声，每径时延分别为0，2，4，8，12，仿真循环10次，16QAM调制方式，插导间隔取5，DFT算法中截取循环前缀长度，所有时间单位设为μs，采用不同算法。得到的实验结果如下所示：

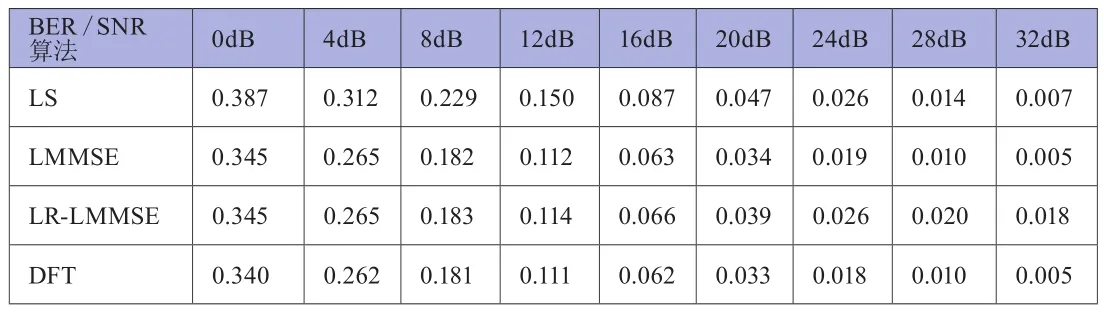
表1 不同算法的SNR-BER结果

分析仿真出的数据结果可以得出不同算法之间的差别。从程序运行所花的时间来看，LMMSE最复杂，花在上面的时间最多，低秩稍次。相同SNR值时，估计质量最好的是DFT，LMMSE与其相比从仿真结果来看差别不大。本次仿真的DFT算法按传统方式截取了循环前缀的长度，如果我们用更为复杂的方式来处理信道响应值理论上可以得到更好的BER。值得注意的是：低秩LMMSE算法随着SNR的升高反而会使BER变差；LS在信噪比低的时候BER比其他几种方法都高，它的估计结果受噪声影响大，在高信噪比的时候效果与其他复杂算法差别不大；以上仿真结果基于特定的实验条件，在实际复杂多变的信道环境中，几种算法之间的差别会更加明显。

7 结束语

毋庸置疑，信道估计技术未来的发展一定会更加完善，本文中介绍的基于导频的估计方法作为信道估计技术的基础，对于我们了解和研究信道估计是很有帮助的。不过，随着通信技术的发展，这种信道估计的方法已稍显浪费，并不是一种性价比高的选择。而本文由于篇幅所限，未能详尽介绍的另外几种估计方法，事实上应用广泛，很多都是时下热点，相信其余的通信学者会给出更加细致和严谨的介绍。

[1] 樊昌信，曹丽娜.通信原理[M]．北京：国防工业出版社，2009

[2] 熊积慧．LS准则下基于DFT插值的OFDM信道估计算法研究[D]．天津大学，2011

[3] 刘钧雷，叶芳，朱琦．OFDM系统基于导频的信道估计[J]．重庆邮电学院学报，2004，16(4):17-20

[4] Taheri Z, Ardebilipour M, Mohammadi M. A. Channel Estimation in Time and Frequency Domain in OFDM Systems [C]. International Conference on Wireless Networks and Information Systems, 2009.

[5] 韩艳春，刘红云，钟雪锋．一种新的低复杂度信道估计算法[J]．电讯技术，2012，52(4)：478-482

[6] 石磊，郭宝龙，李小平等．一种低复杂度LMMSE信道估计算法[J]．西安电子科技大学学报（自然科学版），2012，39(2)：24-28

[7] Xiaodai Dong , Wu-Sheng Lu, Anthony C. K. Soong Senior Member. Linear Interpolation in Pilot Symbol Assisted Channel Estimation for OFDM [J]. IEEE Transactions On Wireless Communications, May5, 2007, 6(5): 1910-1920.

[8] 徐以涛，张玉明，陈卫．16QAM-OFDM系统的迭代信道估计[J]．解放军理工大学学报（自然科学版），2007，8(1)

[9] MORELLI M, MENGALI U. A comparison of Pilot-Aided Channel estimation methods for OFDM system [J]. IEEE Transactions on Signal Processing, 2001, (12): 3065-3073.

[10] 王俊峰，孙江峰．通信原理MATALB仿真教程[M]．北京：人民邮电出版社，2010

[11] 马玉峰．OFDM系统中基于导频的信道估计算法性能分析[J]．科技视界，2012，(14)：171-173

Discussion on Several Common Channel Estimation Algorithms Based on Pilot Signal in OFDM System

Xu Xiaoxin, Jia Yizhen
(China Satellite Communications Corporation, Beijing, 100094)

Because of the complex channel environment, wireless communication systems have great randomness, and the bit error rate is often very high. Whether we can obtain detailed channel information to improve the bit error rate at the receiver is an important index to measure the performance of a wireless communication system. This paper addresses the channel estimation techniques based on pilot signal in orthogonal frequency division multiplexing (OFDM) systems and analyzes several common channel estimation algorithms in OFDM systems.In this paper, we will use MATLAB to simulate several commonly used estimation algorithms of simulation channel and compare them.

Channel estimation; OFDM system; The Least Squares Algorithm; Pilot signal

10.3969/J.ISSN.1672-7274.2017.11.004

TN927

1672-7274（2017）11-0014-05

徐筱昕，毕业于华北电力大学通信工程专业，工学学士，现就职于中国卫通集团有限公司业务运行中心。