基于粒子群算法的拆装机器人逆解研究*

贺倩倩，来跃深，刘梦军，常 宏

(1.西安工业大学 机电工程学院，西安 710021； 2.深圳市北辰亿科科技有限公司 西安研发中心，西安 710065)

基于粒子群算法的拆装机器人逆解研究*

贺倩倩1，来跃深1，刘梦军1，常 宏2

(1.西安工业大学 机电工程学院，西安 710021； 2.深圳市北辰亿科科技有限公司 西安研发中心，西安 710065)

为了使连续生产线工件拆装实现自动化，设计了一种满足工业需求的关节型拆装机器人，并对其样机加工装配。采用D-H法将机器人的三维模型转化为连杆坐标系，通过坐标变换求出机器人的运动学正解。由于机器人结构中连杆关联的原因，采用常规的逆变换法和几何法不能求出逆解，因此提出以“目标点位姿误差最小”为目标函数，各关节转角极限为约束条件，利用粒子群优化算法，对机器人的逆解求最优解。最后，通过对机器人位姿点和连续运动轨迹进行逆解求解验证并对其运动过程仿真分析。实验结果表明该方法求逆解速度快、精度高，能够满足规划的路径，克服了传统方法仅适应于特殊构型机器人的逆解的不足，解决了该机器人的逆解求解。

机器人；运动学；逆解；粒子群算法

0 引言

随着工业生产中自动化改造的需求，工业机器人已广泛应用于各个领域的工业现场。对于工业机器人的结构类型大部分为串联型，其逆解求解过程是研究过程中的关键部分。不同结构类型的机器人求解方法也不同，通常的逆解求解方法包括逆变换法和几何法[1]。逆变换法为较常用的方法，利用矩阵的逆变换分别乘以已知矩阵的方法，对应元素相等求解未知解并回带得到各关节变量的值，其特点为计算量大，求解复杂，且只能针对特定结构的机器人。几何法是利用机器人连杆之间的数学关系，转化成求解平面几何问题，适应于结构较简单直观的机器人。由于本文设计的拆装机器人的特殊结构，用以上方法不能很好的求出逆解，因此，提出“目标点位姿误差最小”为目标函数，各关节转角极限为约束条件，利用粒子群优化算法，对机器人的逆解求最优解。

1 拆装机器人结构设计

本文针对现有连续生产线上的工件焊接时进行拆装的需求，设计了一台拆装机器人代替人工工作。其生产线运动如下：工件(铜管)整齐地排列在直线式链条上的工装上，相邻工件的距离为40mm。当链条以10mm /s的速度匀速运行，铜管通过感应器进行加热焊接，焊接完毕机器人对其进行抓取，水平跟踪运行链条的同时把工件拆出放置在固定的位置。

根据上述连续生产线的实际情况，需要设计满足工作要求和尺寸要求的拆装机器人，其机器人的工作半径为400mm。根据实际要求对其设计加工组装后得到拆装机器人的实物模型，如图1所示。机器人整体采用串联型连杆结构[2]，主要包括底座和腰部的旋转、大臂的摆动、小臂的摆动和手爪相对腕部的旋转，共4个自由度。底座与腰部之间的旋转为了满足工件抓取后回转放置功能；大臂安装在腰部的两侧，摆动实现末端的前后移动；小臂通过连杆机构安装在大臂的后端，摆动实现末端的上下移动；手爪安装在腕部，绕其转动满足在抓取工件后保证水平跟踪一段位姿；腕部是采用双平行四边形连杆结构控制运动过程中的水平性[3]。另外，各个驱动电机极限位置处都装有接近开关，在工作过程中碰到接近开关后急停保证工作的安全性。

图1 拆装机器人实物图

2 运动学分析

2.1 坐标系建立

采用D-H法[4]对上述的拆装机器人建立坐标系，如图2所示。取机器人底座的中点为原点坐标系，其他的坐标系在相邻关节连接处，相邻的坐标系之间的关系用坐标变换矩阵来描述，最终得到末端点关于原点坐标系的矩阵变换。

图2 拆装机器人连杆坐标系

根据连杆长度参数与坐标系得到拆装机器人的连杆变换参数，如表1所示。

其中：αi-1表示连杆扭转角；ai-1表示连杆的长度；θi表示连杆之间的夹角；di表示连杆之间的距离；d1=138mm，d2=135mm，d3=160mm，d4=49.5mm，d5=19mm，d6=30mm。

表1 连杆坐标变换参数表

2.2 运动学正解

机器人的运动学正解指输入各关节的转动角度参数，得到末端的位姿。机器人连杆变换矩阵的通用表达式：

(1)

将表1中的参数代入公式(1)中,根据坐标变换公式0T5=0T1·1T2·2T3·3T4·4T5得，末端相对于原点的坐标变换矩阵为：

其中:

px=d6·c0·(c12·c3-s12·s3)·c4-d6·s0·s4+d4·c0·
c12·c3-d4·c0·s12·s3+d5·c0·c12·s3+d5·c0·
s12·c3+d5·c0·c1·c2-d5·c0·s1·s2+d2·c0·c1

(2)

py=d6·(s12·c3+c12·s3)·c4+d1+d4·s12·c3+d4·
c12·s3+d5·s12·s3-d5·c12·c3+d3·s1·c2+d3·
c1·s2+d2·s1

(3)

pz=d6·s0·(s12·s3-c12·c3)·c4-d6·c0·s4-d4·s0·
c12·c3+d4·s0·s12·s3-d5·s0·c12·s3-d5·s0·
s12·c3-d3·s0·c1·c2+d3·s0·s1·s2-d2·s0·c1

(4)

式中：si=sinθi;ci=cosθi;s12=c1·s2+s1·c2；

c12=c1·c2-s1·s2；矩阵0T5为机器人末端的位姿；Px,Py,Pz为机器人末端的位置坐标。

3 运动学逆解

机器人的逆解指的是已知机器人末端的位姿求出每个关节对应的角度，是机器人控制中必不可少的一部分。根据上述介绍的机器人结构中的连杆关联结构导致不能用几何法和解析法求出机器人的逆解，因此本文提出“目标点位姿误差最小”为目标函数，各关节转角极限为约束条件，利用粒子群优化算法，对机器人的逆解求最优解[5-6]。

3.1 建立数学模型

根据上述提出的“目标点位姿误差最小”的求解目标，利用求出的机器人正解的末端位姿公式与期望的位姿的距离建立数学模型，其中位姿包括位置和姿态，由于位置和姿态在数量级上的差距，引入惩罚因子使其满足整体误差最小[7-8]。其目标函数为：

s.t.Px(θ0,…θ4)=Px;Py(θ0,…θ4)=Py;
Pz(θ0,…θ4)=Pz;F-160°≤θ0≤160°;10°≤θ1≤90°;
-145°≤θ2≤45°;θ3=-θ1-θ2;-120°≤θ4≤120°

(5)

3.2 算法描述

本文采用粒子群算法[9]对上述目标函数求解，首先定义一群满足约束条件的随机解，通过每一组解在一次迭代中的求得当前最优值和所有组粒子的全局最优值的比较来确定满足目标函数的对应解。粒子的更新通过下面的速度更新式子和位置更新式子：

v(i)=w·v(i)+c1·rand()·(y(i)-x(i))+c2·
rand()·(pg-x(i))
x(i)=x(i)+v(i)

(6)

其中,v(i)为第i个粒子的速度，w为惯性权重，c1，c2为学习因子，rand()为0-1之间的随机数，y(i)为第i个粒子的当前最优值，x(i)为第i个粒子的当前位置，pg为全局的最优值。

利用粒子群算法求解机器人逆解的具体步骤流程图如图3所示。

图3 逆解算法流程图

利用上述算法，采用粒子群寻优思想，求出一组位姿对应的逆解，在matlab中编程验证。

4 验证

拆装机器人的运动学逆解通过以下两方面进行验证。一方面是随机取一组机器人末端位姿，通过在matlab中对逆解算法编程，经过多次运行，观察结果的误差范围；另一方面对其一个连续运动轨迹进行规划，求出其逆解并在adams中进行驱动函数添加，得到末端位移曲线，验证其是否满足轨迹要求[10]。

4.1 位姿点验证

取机器人末端一组位姿Px=247.3,Py= 155.9,Pz= -142.8,nx=0.5,oy=0.732,取粒子群数为100，迭代次数50次，运行5次后，收敛曲线如图4所示，逆解结果如表2所示。

图4 适应度值收敛曲线

角度12345θ029．999330．002930．006730．002929．9999θ160．000459．988759．997459．999259．9977θ2-90．0008-89．9997-89．9963-89．9976-89．9985θ40．0098-0．0325-0．0637-0．0205-0．0039f1．3422e-82．6762e-78．9268e-71．9257e-71．4159e-7

从上述的结果可以看出每次运算各个关节角度的误差较小，都接近一个值，且整体位姿误差可达e-7,该位姿对应的关节的角度分别为θ0=30°,θ1=60°,θ2=-90°，θ3=30°,θ4=0°，且目标函数即适应度值的曲线有很好的收敛性。

4.2 连续轨迹验证

根据机器人实际运动的需求，对其运行路径做分段规划，其运动时间，末端坐标以及对应的角度如下表3所示，其中角度利用上述的求逆解方法得出的。

表3 路径规划逆解结果

根据表3中的路径规划，对其整个运动过程进行adams仿真分析，将表3求出的逆解添加在机器人的各关节的驱动函数中，整个仿真时间为4s,后处理后得到机器人末端点的x,y,z方向位移曲线如图5所示。

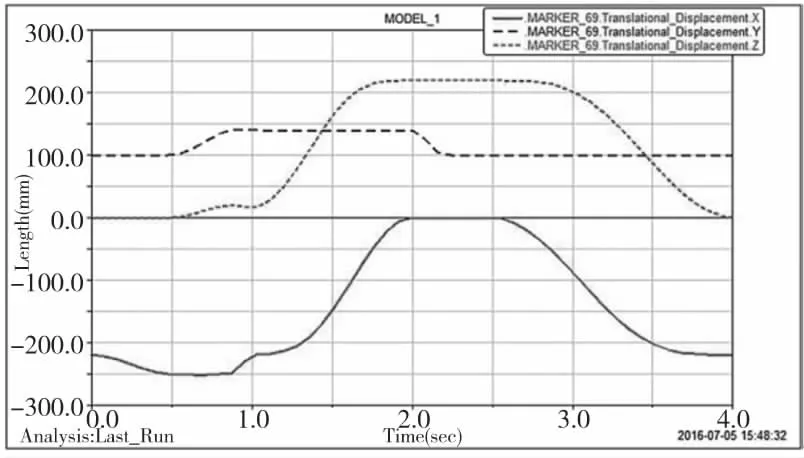
图5 末端的位移曲线

从图5中可以看出机器人末端的x,y,z方向位移坐标均满足整个运动规划过程，验证了利用上述算法求解的逆解的正确性。

5 结论

本文针对项目合作公司提出的需求设计了适应于特定生产线的拆装机器人，解决了特殊行业的工件拆装长期由人工完成的效率低、危害大、成本高的问题。其次，提出了适应于这种关联性结构机器人的逆解求解方法，可应用于不能用常规方法很好的求出逆解的机器人。最后，设计了逆解求解算法，并编程实现随机位置逆解求解验证后，能够保证末端达到预期的位置。该方法相对于传统的求解逆解方法，其计算量较小，舍去了繁杂的公式推导；可运用于特殊构型的机器人逆解求解中；求解速度快，算法有很好的收敛性，结果满足精度要求。

[1] 王光道，刘荫忠，孙维堂.基于加权优化的机器人逆向运动学求解[J].组合机床与自动化加工技术，2016(5):1-3.

[2] 叶辰雷.码垛机器人的结构优化及轨迹规划研究[D].北京:北京邮电大学,2014.

[3] 姚猛，韩宝玲，罗庆生. 工业码垛机器人机构设计与运动学分析[J]. 组合机床与自动化加工技术, 2011(5):31-33.

[4] 蔡自兴.机器人学[M].北京：清华大学出版社,2009.

[5] Y Wang,L Sun,W Yan,et al. An Analytic and Optimal Inverse Kinematic Solution for a 7-DOF Space Manipulator[J]. Robot,2014(5):592-599.

[6] 王战中,杨长建,刘超颖,等.MATLAB环境下六自由度焊接机器人运动学逆解及优化[J].机械设计与制造，2013(7):182-184.

[7] 孙恒辉，赵爱武，李达,等. 基于新旋量子问题改进一类6R串联机器人逆解算法[J].机械工程学报,2016,52(1):79-86.

[8] Damas B,Santors-Victor J.An online algorithm for simultaneously learning forward and inverse kinematics[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2012: 1499-1506.

[9] 刘衍民.一种求解约束优化问题的混合粒子群算法[J].清华大学学报(自然科学版),2013，53(2):242-246.

[10] 李爱成，唐火红，冯宝林. 关节式码垛机器人运动学分析与动力械设计,2013,30(10):16-20.

StudyontheInverseKinematicsofDisassemblingRobotBasedonParticleSwarmOptimization

HE Qian-qian1,LAI Yue-shen1,LIU Meng-jun1,CHANG Hong2

(1.School of Mechatronic Engineering,Xi′an Technological University,Xi′an 710065,China; 2.Xi′an R & D Center, PO LARIS ETek, Xi′an 710065，China)

To realize automation for artifacts disassembled in continuous production line, designed an articulated disassembling robot which meet industrial requirements, and the prototype is processed and assembled.The three dimensional model of the robot is transformed into the link coordinate system by using D-H method, forward kinematics of the robot is obtained by means of coordinate transformation. The reason for the connection of the robot links in the structure, inverse solution can′t be obtained by using the conventional inversion method and the geometric method. Regarded “the error of target′s position-orientation is minimum” as objective function is proposed, the limit of each joint angle is the constraint condition，using particle swarm optimization algorithm to find optional solution of the robot′s inverse solution. Finally, the inverse solution is verified by the robot pose and the continuous trajectory, then simulate and analyse the motion process. The results of the experimental show that the method is fast and accurate, be able to meet the planning path, overcome the shortcomings of traditional methods which only adapt to the inverse solution of special robot, the inverse solution of the robot is solved.

robot; kinematics; inverse solution; particle swarm optimization

1001-2265(2017)11-0008-03

10.13462/j.cnki.mmtamt.2017.11.003

2017-01-23；

2017-03-17

陕西省科学技术厅工业攻关项目(2014k06-26)

贺倩倩(1994—)，女，西安人，西安工业大学硕士研究生，研究方向为机电系统设计及控制，(E-mail)18392066086@163.com。

TH165;TG659

A

(编辑李秀敏)