基于IGOWSA算子的优性组合预测模型

刘 攀，冯长焕

（西华师范大学 数学与信息学院，四川 南充 637002）

基于IGOWSA算子的优性组合预测模型

刘 攀，冯长焕

（西华师范大学 数学与信息学院，四川 南充 637002）

将诱导广义有序加权平均（IGOWA）算子与正弦函数相结合，提出了诱导广义有序加权正弦平均（IGOWSA）算子的概念，研究了该算子的一些优良性质．同时基于IGOWSA算子构建了新的组合预测模型，从理论上证明了该模型是优性组合预测模型，比单一模型的精度更高．最后给出了实例分析，结果显示其5种误差指标均明显小于各个单一预测模型．

诱导集成算子；IOWSA算子；IGOWSA算子；组合预测

0 引言

自Bates等[1]首次提出组合预测的概念以来，组合预测模型越来越受到预测研究者的重视[1-12]．这是因为组合预测模型是将不同单一预测模型进行了适当的组合，克服了单一模型不能反映数据的所有信息的缺陷．它能有效地组合各个单一模型的信息，更加全面反映数据的特征．传统组合预测模型根据不同单一预测模型赋予不同的权重，同一单一预测模型在各个时点的权重相同，赋权的方法主要有算数平均法、方差倒数法、残差倒数法、最优权法等[1-4]．但是对于同一单一预测模型而言，它可能在某个时点的预测误差较小，而在另一时点的预测误差较大．Yager[4]和陈华友[5]提出了基于诱导信息的系列有序集成算子，使这一问题得到解决．周礼刚[6]在Yager和陈华友研究的基础上提出了几种广义信息的集成算子．此后，文献[7-10]基于各种相关性指标对文献[4-6]的集成算子进行了拓展，文献[11，12]把集成算子推广到区间组合预测．当前，集成算子已经成为预测研究的一个热门方向，并获得了广泛的拓展和应用．本研究在诱导广义有序加权平均（IGOWA）算子的基础上提出诱导广义有序加权正弦平均（IGOWSA）算子的概念，建立新的组合预测模型，以期提高预测的精度．

1 IGOWSA算子

定义 1 设 xOWSA，W：Rm→R 为 m 元函数，W=（w1，w2，…，wm）T是与 xOWSA，W有关的加权向量，满wi≥0，i=1,2，…，m．若：

其中bi是a1，a2，…，am中按从大到小的顺序排列的第i个大的数，则称函数xOWSA，W为m维有序加权正弦平均算子，简记为OWSA算子．

定义 2 设（〈v1，a1〉，〈v2，a2〉，…，〈vm，am〉）为 m 个二维数组，令：

其中v-index(i)是v1，v2，…，vm中按从大到小的顺序排列的第i个大的数的下标，则称函数xIOWSA，W是由v1，v2，…，vm所产生的m维诱IOWSA算子，vi称为ai的诱导值．其他符号说明同定义1．

定义3 称

为m维广义有序加权正弦平均算子，简记为GOWSA算子．其中λ是不为0的参数，其他符号说明同定义1．定义4 称

为由v1，v2，…，vm所产生的m维IGOWSA算子．符号说明同定义1-定义3．

根据上述定义，当v1＞v2＞…＞vm时，IGOWSA算子退化为GOWSA算子；当λ=1时，IGOWSA算子退化为IOWSA算子．同时当λ=1时，GOWSA算子退化为OWSA算子．因此OWSA算子、IOWSA算子和GOWSA算子都是IGOWSA算子的特殊形式．下面只研究IGOWSA算子的性质及组合预测模型．

2 IGOWSA算子的性质

当 λ＞0 时，（7）式大于等于 0，所以 λln g（〈v1，a1〉，〈v2，a2〉，…，〈vm，am〉）关于 av-index(i)单调递增，从而 g（〈v1，a1〉，〈v2，a2〉，…，〈vm，am〉）关于av-index(i)递增，f（〈v1，a1〉，〈v2，a2〉，…，〈vm，am〉）关于av-index(i)单调递增.

当 λ＜0 时，（5）式小于等于 0，所以 λln g（〈v1，a1〉，〈v2，a2〉，…，〈vm，am〉）关于 av-index(i)单调递减，从而 ln g（〈v1，a1〉，〈v2，a2〉，…，〈vm，am〉）关于av-index(i)递增，f（〈v1，a1〉，〈v2，a2〉，…，〈vm，am〉）关于av-index(i)单调递增．

性质 2（置换不变性） 设 f为 IGOWSA 算子，（〈v1′，a1′〉，〈v2′，a2′〉，…，〈vm′，am′〉）为二维数组（〈v1，a1〉，〈v2，a2〉，…，〈vm，am〉）的任意置换后的二维数组，则：

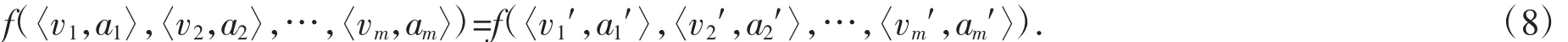
证明：因为（〈v1′，a1′〉，〈v2′，a2′〉，…，〈vm′，am′〉）是（〈v1，a1〉，〈v2，a2〉，…，〈vm，am〉）的置换后的数组，则 av-index(i)=

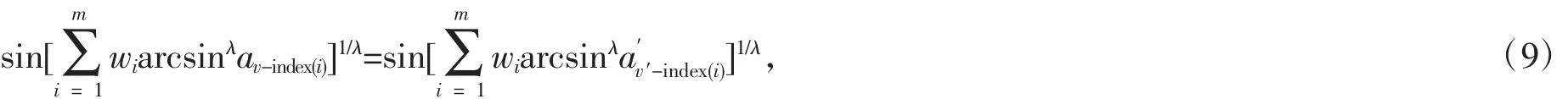
根据定义4，性质2得证．

因为 ai≥ai′，所以 aindex(i)≥，故：

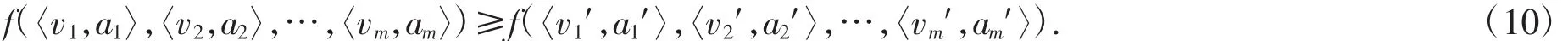
性质3（幂等性） 设f为IGOWSA算子，若ai=a，i=1,2，…，m，则：

证明：若 ai=a，则 av-index(i)=a，从而有：

性质4（介质性） 设f为IGOWSA算子，则：

证明：根据性质1和性质3：

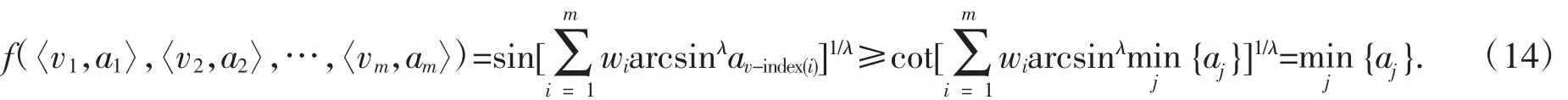
同理可证：

3 基于IGOWSA算子的组合预测模型

设某个指标序列的实际值为xt，t=1,2，…，n，存在m种单一模型对其进行预测，xit为第i种模型在第t时刻的预测值，vit为第i种预测模型在第t时刻的预测精度[5]．

由于反正弦函数的定义域为[-1，1]，数据序列的值域可能不在[-1，1]范围内，需要对数据进行标准化处理．选择：

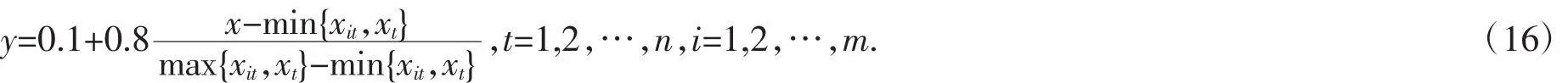
作为规范化处理函数，把数据序列规范在[0.1，0.9]内．处理后的数据仍记为xit，xt．

定义5 令：

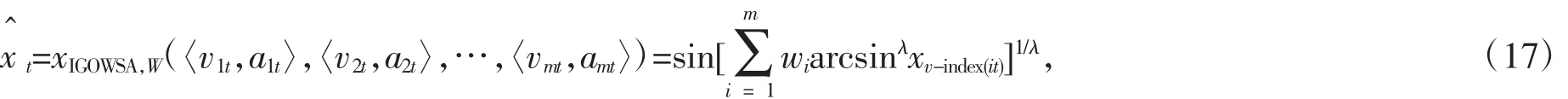
定义 6 称 eit=arcsin-arcsin为第i种预测方法在第t时刻的反正弦λ次幂的预测误差；称et=arcsinλxt-arcsinλx＾t为IGOWSA组合预测值在第t时刻的反正弦λ次幂的预测误差．

要使得n个时刻组合预测值的反正弦λ次幂的预测误差的平方和s最小，其中：

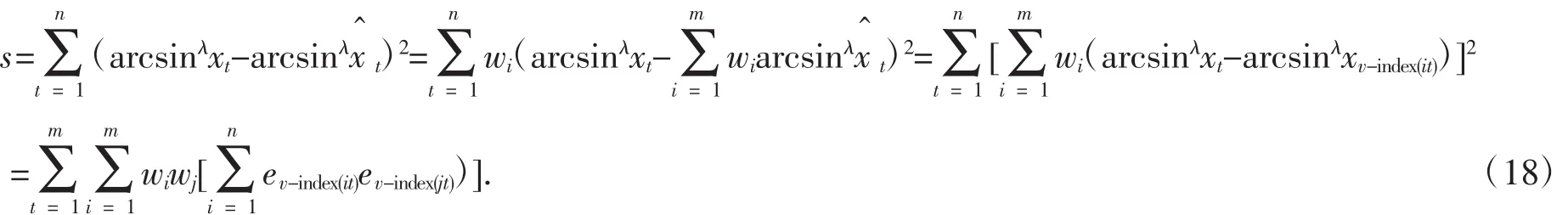
因此基于IGOWSA算子的组合预测模型可以表示为如下优化模型：

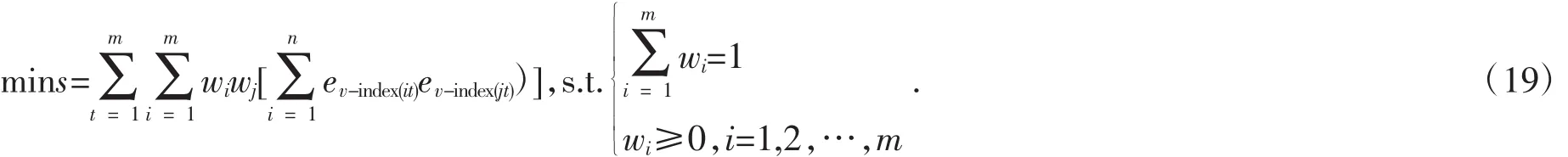
（19）式实际上是一个二次规划问题，利用Lingo或MATLAB等软件可以求解．对求解出来的xt进行反归一化处理，可以得到最终组合预测结果．

根据定义2、定义4和定义5，基于IOWSA算子和IGOWSA算子的组合预测模型依据各单一模型的精度不同，把各个时点的不同预测值按照对应精度从大到小的顺序重新排序．这种基于诱导精度的集成算子能在一定程度上解决“同一单一模型在某个时点的误差较小，而在另一时点的误差较大”的缺陷．下面从理论上给出证明．

定义7 设vit为第i种预测模型在第t时刻的预测精度（t=1,2，…，n，i=1,2，…，m），vt为组合预测模型在第 t时刻的预测精度．∀t∈{1,2，…，n}，若满足 vt≥maix {vit}，称该组合模型为优性组合预测模型；若满足miin {vit}≤vt≤maix {vit}，称该组合模型为非劣性预测组合模型；若满足miin{vit}≥vt，称该组合模型为劣性预测组合模型．

性质5 设f为IGOWSA算子，则基于f的组合预测模型为优性组合预测模型．

根据定义 4，vit≤vindex(it)，所以△it≥△index(it)．并且△index(it)≥△index(jt)，∀i＞j.

根据性质1和性质3，当i=1时，

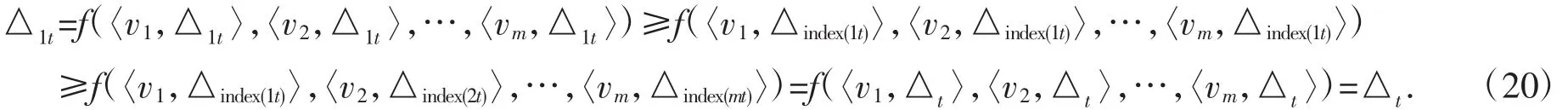
同理，当 i=2,3，…，m 时，△it≥△t．故 vt≥{vit}，基于f的组合预测模型为优性组合预测模型．

4 实例分析

为了说明IGOWSA算子的有效性，利用文献[8，9]中的数据进行验证，具体数据如表1所示．

取λ=1，λ=0.9和λ=0.5，对表1中的数据分别建立基于IOWSA算子组合预测模型，预测结果如表2所示．

为了检验模型的预测效果，选择5种误差指标作为模型好坏的评价体系：

具体结果如表3所示．根据表3可知，取λ=1，λ=0.9和λ=0.5的基于IGOWSA算子的组合预测模型的各项误差指标均明显小于单一预测模型的误差指标，并且在一定程度上比文献[8，9]的组合预测模型误差更小，稳定性更好，结果令人满意．

表1 某指标的实际值和各单一模型预测值

表2 不同参数IGOWTA组合预测模型预测结果

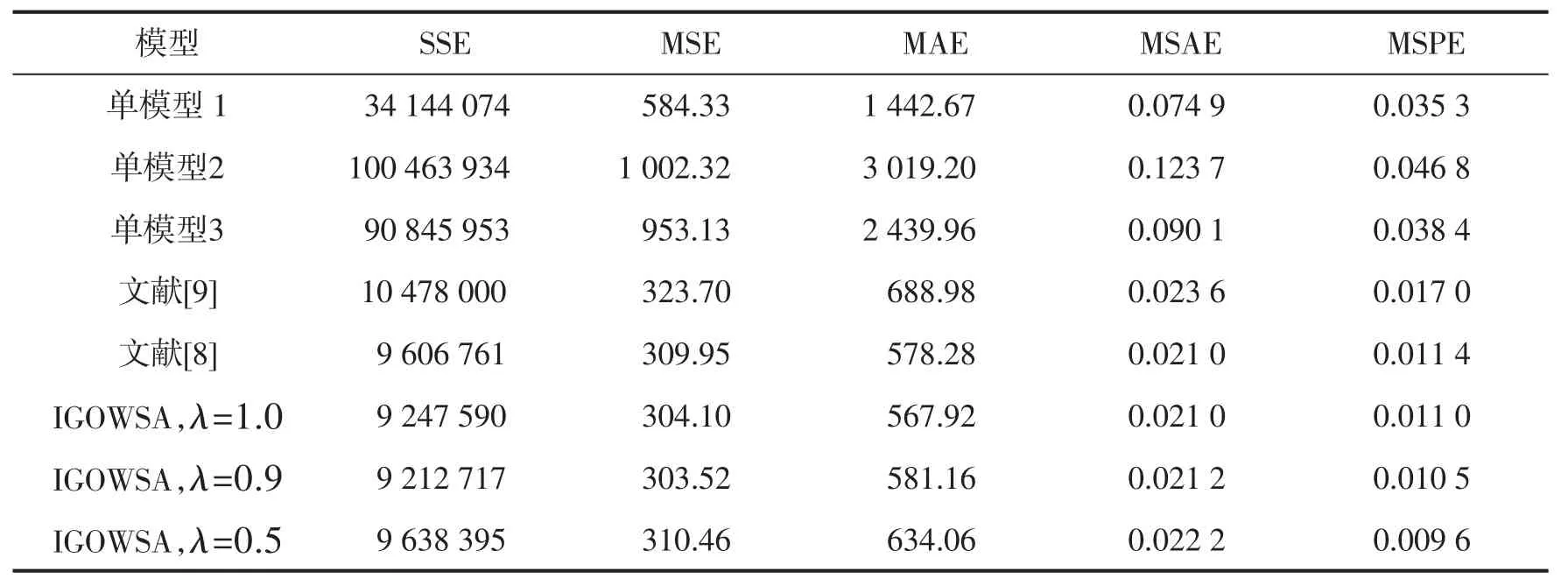
表3 不同模型预测误差比较

5 结束语

提出了有序加权正弦系列集成算子：OWSA算子、IOWSA算子、GOWSA算子和IGOWSA算子，讨论了IGOWSA算子的一些优良性质，建立了基于IGOWSA算子的新的优性组合预测模型．根据表3，参数的取值对组合预测模型的结果有重要的影响，如何确定使模型最优、误差最小，是今后研究的方向.

[1]BATESJM，GRANGERCW.The Combination of Forecasts[J].Journal of the Operational Research Society，1969，20（4）：451-468.

[2]翟静，曹俊.基于时间序列ARIMA与BP神经网络的组合预测模型[J].统计与决策，2016，（4）：29-32.

[3]薛倩，牟凤云，涂植凤.组合预测方法在重庆市GDP预测中的应用[J].重庆工商大学学报（自然科学版），2017，34（1）：56-63.

[4]YAGERRR.Induced Aggregation Operators[J].Fuzzy Setsamp;Systems，2003，137（1）：59-69.

[5]陈华友.组合预测方法有效性理论及其应用[M].北京：科学出版社，2008：166-196.

[6]周礼刚.几类广义信息集成算子及其在多属性决策中的应用[D].合肥：安徽大学，2013：13-136.

[7]石琼强，杨桂元.基于L1范数IOWGA算子的大学生就业信心指数组合预测模型[J].湖北文理学院学报，2014，35（2）：8-11.

[8]储震，杨桂元，吴齐.基于灰关联度的IGOWLA算子中国楼市库存的预测分析[J].佳木斯大学学报（自然科学版），2016，34（4）：599-602.

[9]孙浩，杨桂元.基于一种贴近度的IGOWLA算子的最优组合预测模型[J].延边大学学报，2017，43（1）：19-24.

[10]姚成，袁宏俊.基于向量夹角余弦的IGOWLA算子组合预测模型[J].怀化学院学报，2016，35（5）：25-29.

[11]胡纪纲，芮源，袁宏俊.基于区间关联度的IOWGA算子的区间组合预测[J].统计与决策，2016，（12）：19-22.

[12]袁宏俊，钟梅，吴庆鹏.基于IGOWLA算子的区间组合预测模型[J].统计与决策，2016，（14）：22-25.

A Superior Combination Forecasting M odel Based on IGOWSA Operator

LIU Pan,FENG Chang-huan
(School of Mathematicsamp;Information,China West Normal University,Nanchong,Sichuan 637002,China)

Combining the induced generalized ordered weighted average(IGOWA)operator with the sine function,the concept of induced generalized ordered weighted sine average(IOWSA)operator is proposed,and some excellent properties of the operator are studied.At the same time,a new combination forecasting model is established based on IGOWSA operator,and it proves that the model is a superior combination prediction model above the single model.Finally,the example analysis shows that the 5 kinds of error indexes are obviously smaller than each single prediction model.

induced aggregation operators;IOWSA operator;IGOWSA operator;combined forecasting

F224.0；O212.1

A

1673-1972（2017）06-0057-05

2017-09-02

南充市社科规划一般规划（NC2013B027）；西华师范大学基本科研项目（14C004）

刘攀（1995-），男，四川资阳人，硕士研究生，主要从事预测与决策、应用数理统计研究.

（责任编辑 钮效鹍）