软商空间及其运算性质

刘用麟，黄秀珠

（武夷学院 数学与计算机学院，福建 武夷山 354300）

软商空间及其运算性质

刘用麟，黄秀珠

（武夷学院 数学与计算机学院，福建 武夷山 354300）

将软集合理论应用到商向量空间中，给出了软商空间的合理定义，并给出具体实例证明了软商空间的存在性。 研究软商空间的运算性质，如两个软商空间的扩展交、限制交和限制差分。最后，研究软商空间的同态性质。

软商空间；扩展交；限制交；限制差分；同态

1 引言

众所周知，现实世界存在许多不准确，不完整或不完全可靠信息，统称不确定信息。因此，在现实生的各个领域，人们需要处理大量的不确定信息。由于经典的数学方法不能有效地处理不确定信息，多年来，研究人员一直在探索科学地处理不确定性信息的有效途径。1965年美国控制论专家Zadeh提出模糊集理论，它是处理不确定信息的一种数学方法。1982年，波兰学者Pawlak提出了粗糙集理论，它是又一种刻划不确定性信息的数学工具。另外概率理论也用来处理一些不确定性信息。但是，这些理论都有自己的困难和问题。Molodtsov[1]认为原因之一可能是这些理论的参数工具不足。 为了克服这些困难，1999年Molodtsov引进了软集的概念作为一种新的处理不确定性信息的数学工具。他同时指出了软集的若干可能应用方向。软集理论提出后，一些学者从不同的角度对软集合开展了广泛深入的研究，取得了较大进展。Maji等[2]应用软集理论于决策分析，Maji等[3]还研究了软集理论的运算。 随后，Ali等[4]指出了文献[3]中所提出的交、并运算的一些问题，并给出了新的运算。Chen等[5]提出了参数约简的一个新定义，并将这个定义与粗糙集理论中相关概念属性约简进行了比较。近年来，Aktas等[6]定义了软群并给出了相关的性质，将软集理论应用到群结构上去。从此，一些学者成功地将软集合理论应用到各类代数系统上，如Feng等[7]提出了软半环，Zhan等[8]提出软 BL代数，Acar等[9]提出了软环，Akram等[10-11]提出了软李代数、软K—代数等概念。本文也对软代数理论作了一些研究[12-14]。已经证明软代数具有与经典代数不一样的性质。

本文将软集合理论应用到商向量空间中，给出了软商空间的合理定义，并用具体实例证明了软商空间的存在性。研究软商空间的运算性质，如两个软商空间的扩展交、限制交和限制差分。最后，研究软商空间的同态性质。

2 预备知识

2.1 向量空间的定义及性质

定义2.1.1[15]令P是一个数域，P中的元素用小写拉丁字母 a，b，c，···来表示。令 V 是一个非空集合，V中元素用小写希腊字母α，β，γ，···来表示。把 V 中的元素叫做向量，而把P中的元素叫做数（标）量，如果下列条件被满足，就称V是P上的向量空间：

1)在V中定义了一个加法，对于V中任意两个向量α，β，有唯一确定的向量与它们对应，这个向量叫做α 与 β的和，并且记作 α+β。即若 α∈ V，β∈ V，则（α，β）→ α+β∈ V。

2)有一个数量与向量的乘法，对于P中每一个数a和V中每一个向量有V中唯一确定的向量与它们对应，这个向量叫做a与α的积，并记作aα。即若a∈P，α∈ V，（a，α）→ aα∈ V。

3)向量的加法和数与向量的乘法满足下列算律。

(1)α+β=β+α；

(2)α+β+γ=α+（β+γ）；

(3)在V中存在一个零向量，记作0，它具有下列性质：对于V中每一个向量α，都有0+α=α；

(4)对于V中每个向量α，在V中存在一个向量α'，使得 α'+α=0，这样的 α'叫做 α的负向量；

(5)a（α+β）=aα+aβ；

(6)（a+b）α=aα+ba；

(7)（ab）α=a（bα）；

(8)1a=a。

定义2.1.2[15]设V是数域P上的一个向量空间，W是V的一个非空子集，若W对于V的加法与数乘作成一个向量空间，则称W是V的一个子空间。

定理2.1.1[15]设W 是数域P上向量空间V的一个非空子集，如果W对于P的加法以及标量与向量的乘法是封闭的，那么W本身也作成P上一个向量空间。

定理2.1.2[15]若V1，V2是向量空间V的两个子空间，那么它们的交V1∩V2也是V的子空间。

性质2.1.1[15]在向量空间V中有以下性质：

1)零元素是唯一的，任一元素的负元素是唯一的，a的负元素记为-a；

2)-（-a）=a；

3)0a=0，(-1)a=-a，λ0=0；

4)如果 λa=0，则 λ=0 或 a=0；

5)α（a-β）=αa-αβ，（α-b）a=αa-ba。

2.2 商空间的定义及性质

定义2.2.1[16]设数域P上的向量空间，W 是V的子空间表示V中关于子空间W的所有陪集作V 成的集合，即在集合V中引进加法和数乘运算：（α+W ）+（β+W ）=（a+β）+W ；k（α+W ）=kα+W ；k∈ P。

可以证明关于上面定义的加法和数乘运算作成数域P上的向量空间，称之为向量空间关于子空间W的商向量空间，简称商空间，记为。

定理2.2.1[16]设V是n维线性空间，W 是它的r维子空间V/W，则商空间的维数为n-r。

定理2.2.2[16]设f是线性空间V到V'的同态映射，W 是 V 的子空间，则是 V'的射，是的子空间，则是 V 的子空间。

定理2.2.4[16]（第一同构定理）设f是线性空间V到V'的满同态，W'是 V'的子空间，则 V/f-1（W'）≅V'/W'。

定理2.2.5[16](同态基本定理)设V是一个线性空间，则V的任一商空间都是V的同态象。即线性空间V与它的每一个商空间V/W 同态。反之，若V'=f（V）是V的同态象，则V'≅V/ker f。

定理2.2.6[16](第二同构定理)设W1，W2是线性空间 V 的子空间，则（W1+W2）/W2≅ W1/（W1∩ W2）。

2.3 软集理论的定义及基本运算

定义2.3.1[1]设U是一个论域，E是参数集，A⊂E，P（U）是U的幂集。若F是A到P（U）的映射，则称（F，A）为U上的一个软集合。

定义 2.3.2[4]设（F，A）和（G，B）是 U 上的两个软集合，定义它们的扩展交为软集合（H，C）。其中，C=A∪ B，且子空间。

定理2.2.3[16]设f是线性空间V到V'的同态映

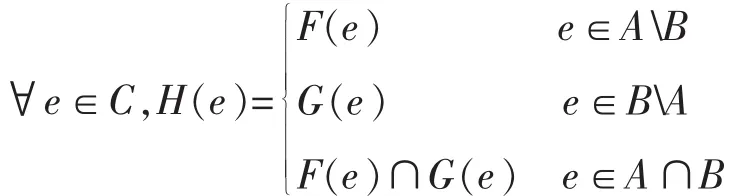
记（F，A）∩E（G，B）=（H ，C）。

定义 2.3.3[4]设（F，A）和（G，B）是 U 上的两个软集合，且A∩B≠φ，

1)定义它们的限制交为软集合（H，C），其中C=A∩ B，且∀ e∈ C，H （e）=F（e）∩ G（e）。记（F，A）∩△（G，B）=（H ，C）。

2)定义它们的限制并为软集合（H，C），其中C=A∩ B，且∀ e∈ C，H （e）=F（e）∪ G （e），记（F，A）∪R（G，B）=（H ，C）。

3)定义它们的限制差分为软集合 （H，C），其中C=A ∩ B，且∀ e∈ C，H （e）=F（e）G （e），记（F，A）∩D（G，B）=（H ，C）。

定义 2.3.4[4]对于两个软集合和（F，A）和（G，B），如果满足下面两个条件：

1）A⊂ B；

2）∀ X∈ A，F（X）⊂ H（X）。

则称（F，A）是（G，B）是的软子集，记为（F，A）⊂ （H，B）。

3 软商空间

3.1 软商空间的定义

为了便于说明，本文中令X是数域P上一个商空间，A是一个非空集合。

定义3.1.1 设（F,A）是数域P上商空间X上的一个软集，如果∀X∈A，F（x）是X的一个子空间，则称（F,A）是X上的一个软商向量空间，简称软商空间。

定义 3.1.2 设（F，A）和（H，B）是商空间 X 上的两个软商空间，如果满足下列两个条件：

1)B⊂ A；

2)∀X∈ B，H （x）是 F（x）的子空间。

则称（H ，B）是（F，A）的软商子空间，记为（H，B）＜（F，A）。

推论 3.1.1 设（F，A）和（H ，B）是商空间 X 上的两个软商空间，当H=F时，仅需满足条件：B⊂A，则（H，B）是（F，A）的软商子空间。

3.2 软商空间的例子

例 3.2.1 设 α1，α2，α3，α4，α5∈ R5，W=L （α1，α2）,商空间 X=R5/W=L（α3+W ，α4+W ，α5+W ）。令

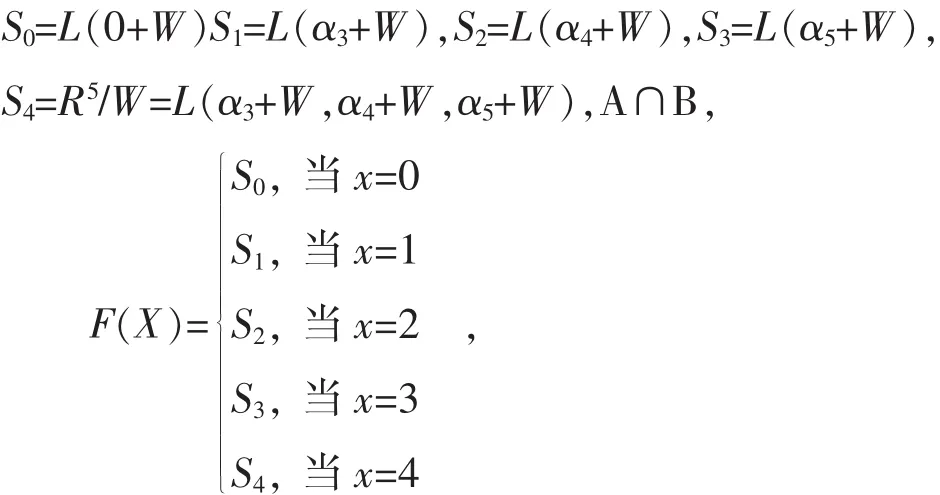
于是 F（0）=S0，F（1）=S1，F（2）=S2，F（3）=S3，F（4）=S4都是X的子空间，所以（F，A）是X上的软商空间。此例说明了软商空间是存在的。

例3.2.2 设M2（F）为数域P上的所有二阶方阵所成的集合，关于矩阵的加法和数乘作成数域P上的向量空间是 M2（F）的子空间，商空间

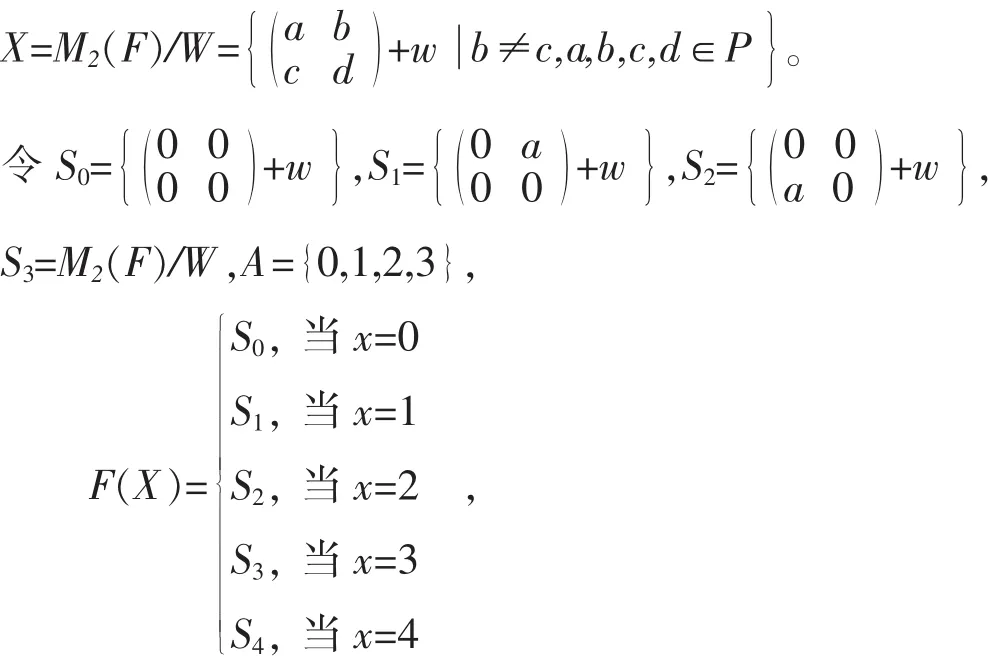
于是 F（0）=S0，F（1）=S1，F（2）=S2，F（3）=S3，都是 X 的子空间，所以（F，A）是X上的软商空间。

4 软商空间的性质

4.1 软商空间的扩展交

引理4.1.1 若A,B均为商空间X的子空间，则A∩B也是X的子空间。

证明：首先，根据 0∈A，0∈B 可知 0∈A∩ B，因此 A∩ B 是非空的。其次，若 α，β∈ A∩ B，即 α，β∈ A，且 α，β∈ B，则 α+β∈ A，α+β∈ B，于是 α+β∈ A∩ B。对α∈ A∩ B，k∈ P，即 α∈ A，α∈ B，那么 kα∈A，kα∈B，因此kα∈A∩B，所以A∩B也是X的子空间。

定理 4.1.1 如果（F1，A1）和（F2，A2）是商空间 X 上的两个软商空间，则（F1，A1）∩E（F2，A2）也是商空间 X上的软商空间。

证明：令（F，A ）=（F1，A1）∩E（F2，A2），其中 A=A1∪ A2，∀x∈A,

因为（F1，A1）和（F2，A2）都是商空间 X 上的软商空间，对∀ x∈ A，则 x∈ A2A1或 x∈ A1∩ A2三者必然成立一个，若 x∈ A2A1或 x∈A1A2则 F（x）=F1（x）或 F2（x），均为 X 的子空间。若 x∈ A1∩ A2，则 F（x）=F1（x）∩F2（x），由引理 4.1.1，F（x）也为 X 的子空间。 因此（F，A）是是X上的软商空间。

4.2 软商空间的限制交

定理 4.2.1 如果（F1，A1）和（F2，A2）都是商空间 X上的软商空间，且 A1∩ A2≠ φ，则（F1，A1）∩△（F2，A2）也是X上的软商空间。

证明：令（F，A ）=（F1，A1）∩△（F2，A2），其中 A=A1∩A2且对∀ x∈ A ，F（x）=F1（x）∩ F2（x）。由于（F1，A1）和（F2，A2）都 X 上的软商空间，所以对∀ x∈A1，有 F1（x）是 X 上的子空间；同理可得∀ x∈ A2，有 F2（x）是 X 上的子空间，因此，对∀x∈A，有F（x）是X上的子空间，从而（F1，A1）∩△（F2，A2）是 X 上的软商空间。

4.3 软商空间的限制差分

定理 4.3.1 如果（F1，A1）和（F2，A2）都是商空 X 上的软商空间，且 A1∩ A2≠ φ，则（F1，A1）∩△（F2，A2），则一定不是商空间X上的软商空间。

证明：令（F，A ）=（F1，A1）∩△（F2，A2），其中 A=A1∩A2且对∀ x∈ A，F（x）=F1（x）F2（x）。由已知，对∀ x∈ A ，F1（x），F2（x）为商空间 X 的子空间，所以 0∈ F1（x），0∈F2（x），故 0∉ F（x）。于是，F（x）不为商空间 X 上的子空间，故（F1，A1）∩D（F2，A2）一定不是商空间 X 上的软商空间。

4.4 软商空间的同态性质

定义4.4.1 设X和Y是数域P上两个商空间，f：A→B是一个映射，若满足：

1)∀ α，β∈ A ，有 f（α+β）=f（α）+f（β），

2)∀ k∈ P，α∈ A 有 f（kα）=kf（α），

则称f是商空间A到B的一个同态映射。若f是满射，则称f是商空间A到B的一个满同态；若f是单射，则称f是商空间A到B的一个单同态；若f是双射，称是商空间A到B的一个同构。

引理4.4.1 设X，Y是两个商空间，如果f：X→Y为从X到Y的商空间同态：

1)若M 为X的子空间，则f（M）为Y的子空间；

2)若L为Y的子空间，则f-1（L）为X的子空间。

证明：设∀y1，y2∈ f（M ），在 M 中存在两个元素 x1，x2使得 y1=f（x1），y2=f（x2），则 y1+y2=f（x1）+f（x2）=f（x1+x2）。由M 为X的子空间可知x1+x2∈ M，从而y1+y2=f（x1+x2）∈ f（M ）；设∀ k∈ P，∀ y∈ f（M ），则 M 中存在 x，使得y=f（x），于是 ky=kf（x）=f（kx），由于 kx∈ M ，所以 ky=f（kx）∈f（M ）。因此 f（M ）为 Y 的子空间。同理可证，f-1（L）为X的子空间。

定理4.4.1 设X，Y是两个商空间，如果f：X→Y为从X到Y的商空间同态，（F,A）是X上的软商空间，则（f（F），A ）是 Y 上的软商空间。

证明：首先由（f（F），A）的定义知（f（F），A）为 Y 上的软集。由（F,A）是X上的软商空间知，对任意的a∈A，F（a）是 X 的的子空间，由引理 4.4.1 可知，f（F（a））为 Y 的子空间，即对任意的 a∈A，f（F）（a）是 Y 的子空间，从而有（f（F），A ）是 Y 上的软商空间。

定理4.4.2 设X，Y是两个商空间，如果f：X→Y为从X到Y的商空间同态，（H，B）是Y上的软商空间，则（F-1（H ），B）为 X 上的软商空间。

证明：首先由（F-1（H ），B）的定义知（F-1（H ），B）为 X上的软集。对任意的b∈B，由（H，B）是Y上的软商空间知 H （b）是 Y 的子空间，因此由引理 4.4.1，f-1（H （b））是 X 的子空间，即对任意的 b∈ B，f-1（H）（b）是 X 的子空间，从而有（f-1（H ），B）为 X 上的软商空间。

定理4.4.3 如果f：X→Y是一个商空间同态，（F，A）和（H，B）是商空间 X 上的软商空间，（F，A）≾（H，B），则（f（F），A）≾ （f（H ），B）。

证明：由（F，A）≾ （H，B）可知 A⊂B，故对∀ x∈ A，有 F（x）是 H （x）的子空间。又由 f是同态映射，有 f（F）（x）=f（F（x））是 f（H （x））=f（H ）（x）的子空间，由定理4.4.1 可知，（f（F），A）与（f（H ）B）为 Y 上的软商空间，再根据定义 3.1.2 可得，（f（F），A）≾（f（H ），B）。

[1] MOLODTSOV D.Soft set theory-first results[J].ComputMath Appl,1999,37(4-5):19-31.

[2] MAJIP K,ROY A R,Biswas R.An application of soft sets in a decision making problem [J].Comput Math Appl,2002,44(8-9):1077-1083.

[3] MAJIP K,ROY A R,Biswas R.Soft set theory[J].Comput Math Appl,2003,45(4-5):555-562.

[4] ALIM I,FENG F,LIU X,et al.On some new operations in softset theory[J].ComputMath Appl,2009,57(9):1547-1553.

[5] CHEND,TSANGECC,YEUNGD S,etal.The parametriza-tion reduction of soft sets and its applications[J].Comput Math Appl,2005,49:757-763.

[6] AKTASH,CAGMAN N.Soft sets and soft groups[J].Information Science,2007,177(13):2726-2735.

[7]FENG F,JUN Y B,ZHAO X.Soft semirings[J].ComputMath Appl,2008,56(10):2621-2628.

[8] ZHAN J,JUN Y B.Soft BL-algebras based on fuzzy sets[J].ComputMath Appl,2010,59(6):2037-2046.

[9] ACAR U,KOYUNCU F,TANAY B.Soft sets and soft rings[J].ComputMath Appl,2010,59(11):3458-3463.

[10]AKRAM M,FENG F.Soft intersection Lie algebras[J].Quasigroupsand Related Systems,2013(21):1-10.

[11] AKRAM M,Al-SHEHRIE N O,ALGHAMDIR S.Fuzzy soft K-algebras[J].Utilitas Mathematica,2013(90):307-325.

[12] LIU Y L,KIM H S.Non-commutative residuated lattices based on soft sets[J].J Intelligentamp;Fuzzy Systems,2015(29):2271–2278.

[13] 刘用麟,黄艺娟.软结合BCI-代数[J].数学进展,2016,45(4):500-508.

[14] LIU Y L,KIM H S,NEGGERS J.Hyperfuzzy subsets and subgroupoids[J].J Intelligentamp;Fuzzy Systems,2017(33):1553-1562.

[15] 王萼芳,石生明.高等代数[M].3版.北京:高等教育出版社,2003:237-262.

[16] 刘用麟.商空间的同构定理及其应用 [J].南平师专学报,2006,25(4):1-4.

（责任编辑：华伟平）

Soft Quotient Space and Its Operational Properties

LIU Yonglin，HUANG Xiuzhu

（School ofMathematics and Computer Science,Wuyi University,Wuyishan,Fujian 354300）

In this paper,the soft set theory is applied to the quotient vector spaces.The concept of softquotient vector spaces is introduced.We show the existence of soft quotient vector spaces by an example.And then we discuss the operation properties of soft quotient vector spaces,such as the extended intersection operation,the restricted intersection operation and the restricted difference operation of two soft quotient vector spaces,and so on.Finally,we research the homomorphism properties of softquotient vector spaces.

softquotient vector space;extended intersection;restricted intersection;restricted difference;homomorphism

O151.2

A

1674－2109(2017)09－0001－05

2017-08-10

福建省科技计划引导性项目（2016Y0077）。

刘用麟（1959-），男，汉族，教授，博士，主要从事逻辑代数和软代数研究。