基于NNG的软测量技术在空气分离中的应用

余旺， 孙凯(齐鲁工业大学 电气工程与自动化学院，济南 250353)

基于NNG的软测量技术在空气分离中的应用

余旺， 孙凯
(齐鲁工业大学 电气工程与自动化学院，济南 250353)

针对空气分离装置，设计了一种基于非负阈值的软测量算法。算法以贝叶斯准则作为模型的评价标准，以v-fold交叉验证法来确定最优非负阈值系数。所设计算法应用于空气分离装置的O2浓度检测，并和最小二乘法进行比较。MATLAB仿真结果表明该算法能够实现O2浓度的精确测量，并且模型精度上优于最小二乘法。

软测量； 变量选择； 非负阈值算法

0 引言

在工业生产中，为获得更多合格的高质量产品，从而提高装置的经济效益，就需要对产品质量或与产品质量密切相关的重要过程变量进行严格控制。然而在过程控制中，存在许多难以或无法直接使用传感器进行检测的变量，如：催化剂活性、干点、某些精馏塔产品成分、反应器中反应物浓度、高炉铁水的含硅量等。为了解决这类变量的测量问题，一般有两种途径：一种是研究新型的传感器以硬件形式实现过程变量的直接在线测量；另一种是目前应用较为广泛的软测量方法[1-2]。

软测量的基本思想是把难以测量或无法直接测量的重要变量(主导变量、响应变量)，选择另外一些容易测量的变量(辅助变量、预测变量)来构造某种数学关系对主导变量进行估计或预测，以计算机软件代替传感器功能。因此又称之为软仪表技术。这种方法具有响应迅速、投资低、维护保养简单等优点。目前工业过程的软测量实现流程主要包括：辅助变量的选择、数据的采集与处理、软测量模型的建立和软仪表的校正。软测量工业实现流程,如图1所示。

辅助变量的选择要通过机理分析以及有关装置和工艺流程来初步确定影响主导变量的相关辅助变量，包括变量类型、变量数目和监测点的选择。这些方面相互作用，互有影响，是由过程特性决定的。此外，在实际应用中还要考虑经济性、维护的难易程度等。应用中，对于线性回归的变量挑选方法主要有前向选择算法、后向选泽算法和逐步回归算法，但当备选变量比较多时，枚举比较的计算量非常大，导致算法效率太低。当前研究较多的是基于系数压缩的变量选择方法，它能同时进行变量选择和参数估计，如非负阈值算法[3-4](Nonnegative garrote，NNG)，套索算法(Least absolute shrinkage and selection operator，LASSO)等。

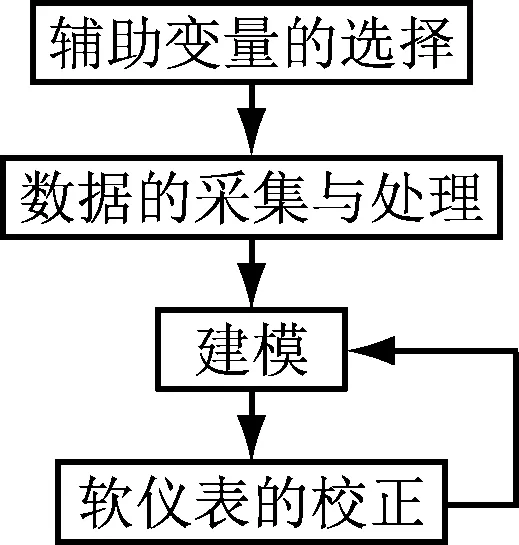
图1 软测量模型

过程数据的处理包括数据的变换和误差处理。通过数据变换，如数据的转换、标度的处理和权函数，可有效改善算法的精度和稳定性，降低原数据的非线性特性，实现对变量动态特性的补偿。误差分为随机误差和过失误差，前者主要使用滤波的方法解决；后者出现的几率虽小，但它的存在会严重恶化数据的品质，甚至导致软测量的失败，这类误差的处理主要有统计假设检验法、贝叶斯法、硬件冗余法等。

软测量的核心问题是建立能够由辅助变量预测主导变量的关联模型。目前，软测量建模方法一般可分为：机理建模、回归分析、状态估计、人工神经网络、模糊数学、基于支持向量机和核函数的方法、过程层析成像和现代非线性系统信息处理技术等。这些方法各有各的适用范围且都不同程度地应用于软测量实践中，有些方法在软测量实践中已有许多成功的应用，后面几种建模方法限于理论研究，目前在过程控制中的应用还比较少。

由于工作点和测量对象特性的变化，已建立的软测量模型也会发生相应的变化，因此必须对软测量模型进行在线校正，才能适应新工况。模型结构的校正一般需要重新采集大量数据，因此比较耗时难以在线进行，为解决模型结构校正耗时长和在线校正的矛盾，研究人员提出了短期学习和长期学习的校正方法。短期学习在不改变模型结构的情况下用新采集的数据对模型中的相关系数进行更新；而长期学习则利用新采集的数据重新建模。

1 空气分离装置介绍

本节对空气分离装置的工作流程进行介绍并列出该装置的18个可测输入变量。空气分离装置的工业流程,如图2所示。

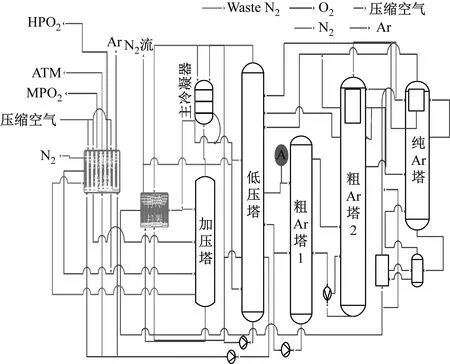
图2 空气分离装置工业流程图

空气分离装置有五个相互协调的蒸馏塔，用来分离压缩空气中的N2，O2和Ar。压缩空气首先注入主热交换器(Main heat exchanger，MHE)中然后再注入加压塔，N2产品流会从加压塔的顶部分离出来，加压塔顶端的产品流经过再冷却系统后又作为粗Ar塔2和纯Ar塔的冷凝剂使用，然后经过低压塔降低压强后和加压塔流出的剩余N2汇合，其中一部分N2产品流经过主冷凝器和再冷凝器得到液化的N2产品，另一部分再次经过MHE得到N2产品。

液化O2产品来自于低压塔底部，经过主热交换系统后用泵进行压缩可分别得到32 kg/cm2的高压O2产品和12 kg/cm2的中压O2产品。Ar产品经过粗Ar塔1、粗Ar塔2和纯Ar塔的3层过滤得到提纯的Ar。

液Ar产品存放在特制的容器中，容器中的液Ar反过来流经主热交换器而气化，以此来降低压缩空气的温度。

在空气分离设备中安装了一个O2浓度的在线检测装置如图中A所示。O2浓度监测的目的一方面是为了保证产品的质量，另一方面是为了防止粗Ar塔2的N2的泄露。如果O2浓度较低，粗Ar塔1的入口处就会聚集大量的N2，这时粗Ar塔2顶端的压强就会增大直到把塔内N2排除为止。另一方面，如果O2浓度过高，那么Ar的产量就会因为Ar浓度的减少而减少。因此，O2浓度在线检测装置的测量值要保持在一定的范围之内，然而，这种在线装置并不能很好的达到这些要求，因此需要一种代替在线分析仪表的软测量方法。

空气分离装置有18个可测输入变量和一个输出变量—氧气浓度。所有的可测输入变量,如表1所示。

表1 空气分离装置的可测输入变量

空气分离装置的预测模型所使用的数据都是在2013年1月1日到6月30日每隔五分钟测得的。其中，一半的数据用来建立预测模型，剩余一半的数据用来测试预测模型的精度。

2 NNG介绍

NNG算法是一种稳定性好，又能对候选变量进行筛选和系数压缩的变量选择方法[3-4]，即它不仅可以压缩候选变量的个数，还可以压缩相应变量的系数。从实际和仿真的结果来看，相比传统的最小二乘回归，NNG拥有较小的预测误差。对于一个回归方程来说，如果其中一个数据的较小变化不会引起预测方程较大的变动，那么称这个过程是稳定的。而子集回归的缺点之一就是稳定性差，例如，N=100，M=40，对变量进行逐步删除可得到一系列的变量子集{xm；m∈ζk}，(|ζk|=k)k=1，…,M。现在移除一个变量(yn，xn)，再进行相同的选择过程也会得到一系列新的变量子集{xm；m∈ζk′}。通常情况下，{ζk′}和{ζk}是不同的，参见文献[6]。也就是说，对于相同的k，单个数据的扰动，就会对预测方程产生巨大的影响。与此相比，如果使用NNG算法，在移除单个数据的情况下，新得到的主导变量的估计和之前的估计不会有较大的偏差[5]。

在统计分析方法中最常用的就是数据的选择性回归分析(subset-selection regression)。也就是在给出的如下数据：{(yn，x1n，…，xMn)，n=1，…,N}，x1，…，xM中的一些变量被淘汰，剩下的变量将用来构造y的预测方程。

数据的选择对于预测方程有两个方面的好处，一是减小预测方程的方差，二是预测方程的简化。众所周知，每增加一个用于构造y的预测方程的变量都会增加预测方程的方差，因此，预测方程中的变量数越少方差就越小。然而需要注意的是，使用的辅助变量太少可能会导致预测结果有较大的偏差。但是如果一个有40个辅助变量的回归方程可以把变量数压缩到5个而不影响预测方程的精度，那么不仅预测方程得到了简化而且还可以知道哪些辅助变量对主导变量y来说是重要的，变量选择的重要性不言而喻。

2.1 最小二乘法

对于线性回归模型,如式(1)。

y=Xβ+e

(1)

(2)

式(2)有唯一最小解的充要条件是XTX或X的秩为p(满秩)。此时得到方程(2)的唯一解为式(3)。

(3)

应用实践表明当变量之间的相关性较高时，最小二乘估计不是很令人满意，具体表现为：

(1) 某些回归系数估计值的绝对值差异较大

(2) 有时回归系数的估计值符号与实际意义相违背

此外，当XTX不可逆时，该方法没有唯一最小二乘估计，且只能应用于线性估计。

2.2 NNG的工作原理

下对{ck}极小化,即解式(4)。

(4)

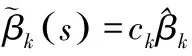
2.3s的选择及预测误差

变量选择的目的就是要找到对y影响较大的辅助变量，还希望由辅助变量对y可能出现的情况进行预测。当把预测作为我们的主要任务时，常把预测误差(平方和)PE(prediction error)(式(5))

(5)

(6)

其中的第一项为由噪声引起的系统本身的固有误差，第二项为模型误差ME(model error)。模型误差的大小反映了不同模型的优劣。最佳的s值就是使PE取得最小的s值[16]。然而，在实践中由于样本数据的限制，PE的值并不是可直接观测到的，我们必须对数据进行重用，对数据进行多次切分来得到较好的估计。V折交叉验证法由于其简洁性和普遍性被认为是一种行之有效的办法。

V折交叉验证法首先是把数据集平均分为V份，每次从V份数据集中拿出一份数据集作为验证集，剩下的V-1份数据集作为训练集，重复进行V次，最后平均V次的结果作为最后泛化误差的估计。通常V的取值为5到10时能得到较好的结果，当V取值太大时，方差也会随之增大；当V取值较小时由于参与训练的样本数据减少会导致预测误差的增大。本文取V=10，即把样本数据平均分为10份，记为A1，…Av。且对于任意子集Aj，都有M(Aj)≈n/V，M为第j个子集中样本的个数，PE的估计值,为式(7)。

(7)

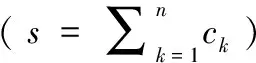
3 仿真结果

图3为用NNG算法对O2浓度的预测结果，结果表明NNG算法能很好地对O2浓度进行预测。

OLS的预测结果，如图4所示。可以看出其预测波动较大，整体上没有NNG拟合的好。

使用NNG算法和OLS算法对空气分离装置的O2浓度进行预测时的平均均方误差(Mean Squared Error，MSE)，如表2所示。

由表2可知，应用NNG算法对O2浓度进行预测比OLS算法的预测精度高。

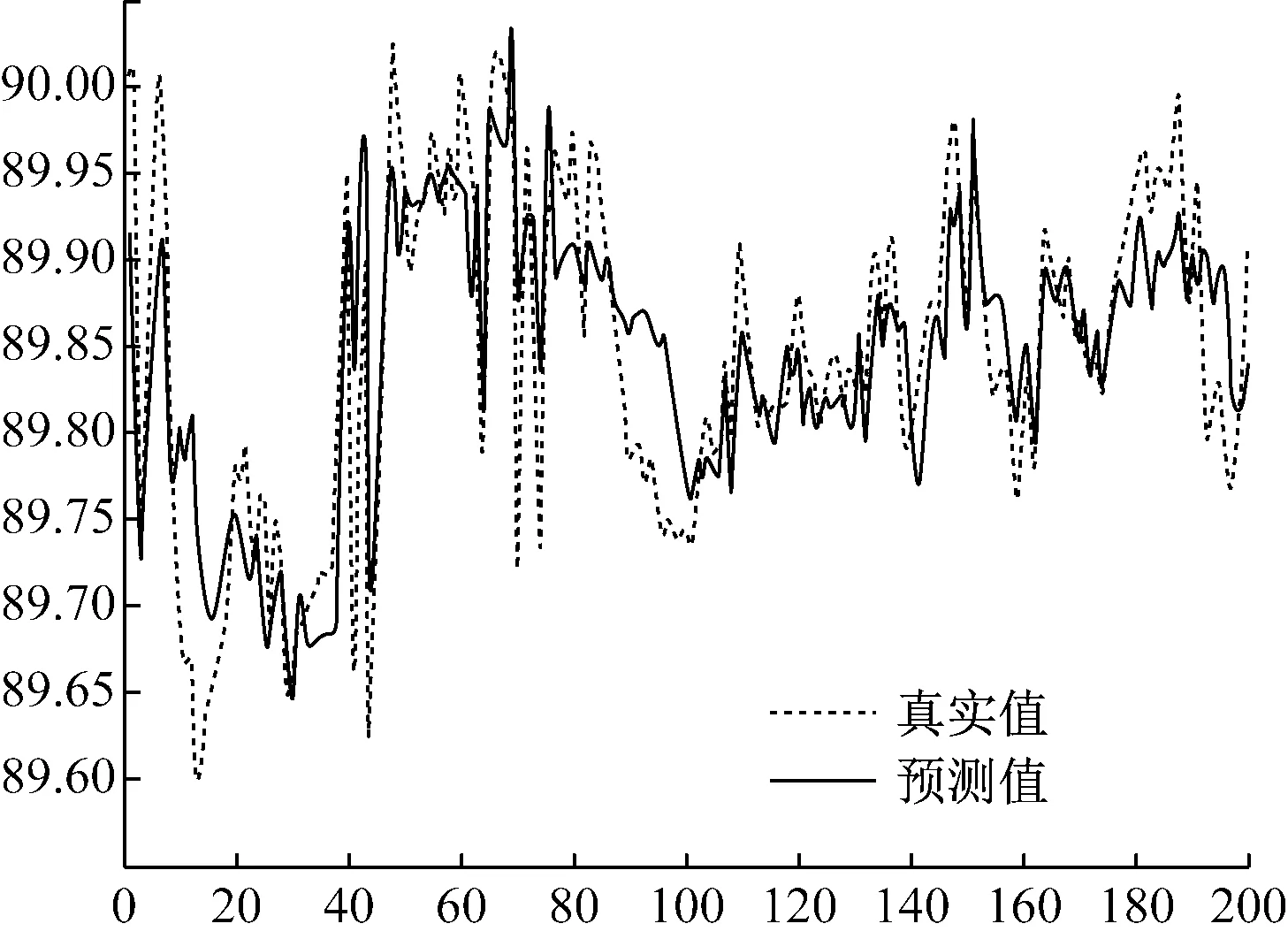
图3 NNG回归预测

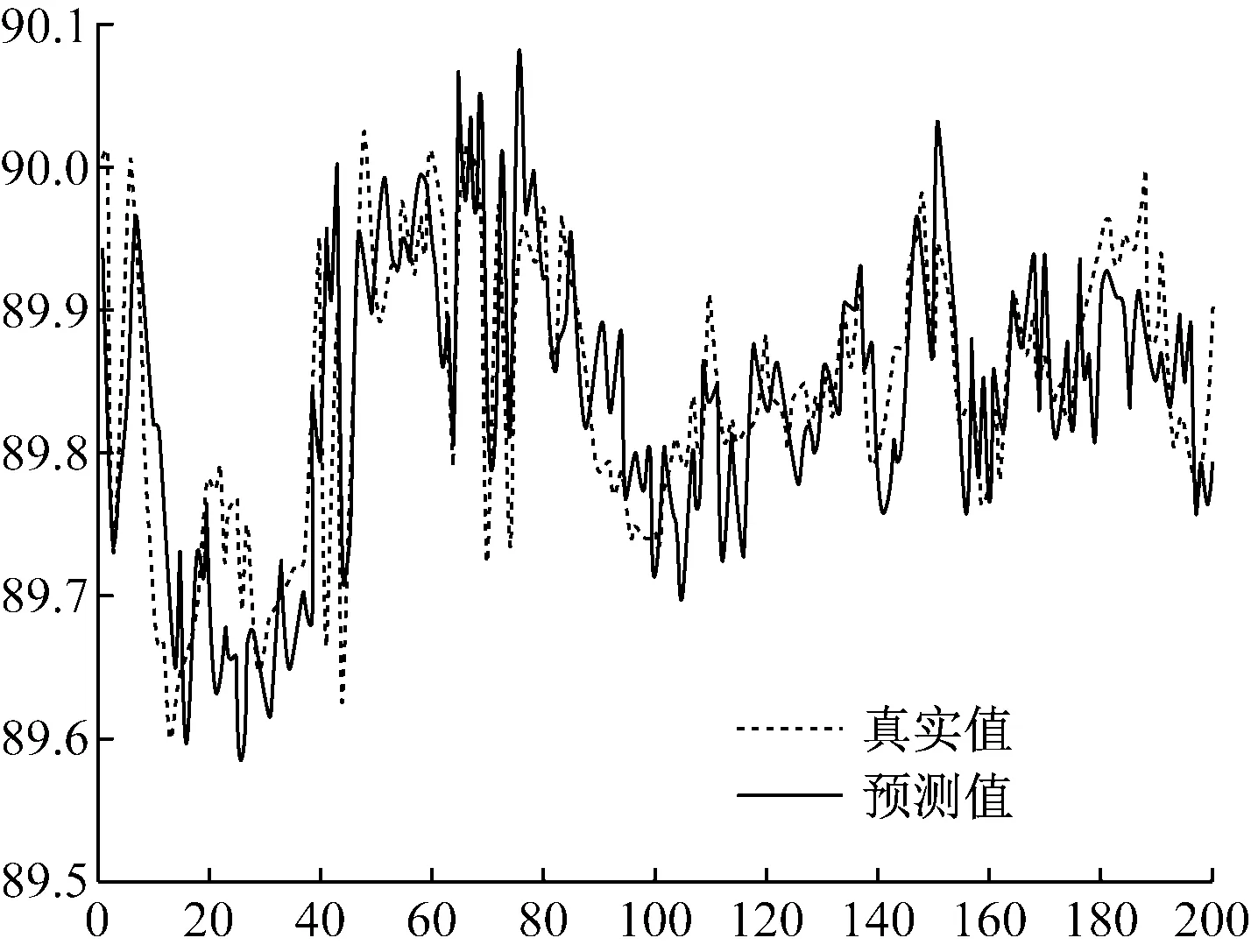
图4 OLS回归预测

表2 NNG和OLS算法对O2浓度的预测精度

为了更直观的比较两种方法的预测效果，把NNG算法和OLS算法的预测误差进行了比较，如图5所示。

图5 NNG和OLS的预测误差比较

由图5可知， NNG的预测误差几乎处处都比OLS的预测误差小，且预测稳定性较高。

应用NNG算法对O2浓度进行与测试时最终筛选出的变量及其相应系数,如表3所示。

表3表明：应用NNG方法对O2浓度进行与测试时，在保证预测精度的基础上共从18的候选变量中选出8个。由系数可知，对O2浓度进行预测时，变量17(低压塔出口处温度)的作用最大，其次是变量7(低压塔流入主热交换器的液O2流量)和3(总液N2流量)。由现场操作经验可知变量17处在采样点A附近，因此，该变量与O2浓度有很高的对应关系。实际上，当在线检测装置A出现故障时，操作人员通常是监测低压塔出口处温度来保证空气分离装置的正常运行。当温度太高时，变量4(回流至低压塔的液N2流量)就会增加，从而达到降温的目的，而变量3(总液N2流量)对变量4有着直接的影响；相反，当A处温度较低时，变量7(低压塔流入MHE的液O2流量)就会减少，从而减少低压塔的热量损失而达到升温的目的。从空气分离装置的工作流程和表2表3可知，NNG算法对预测变量的筛选是十分正确的。

表3 NNG变量选择结果

4 总结

本文首先介绍了软测量技术及其优点。其次介绍了NNG算法和最小二乘法并应用交叉验证法对s值进行了确定。最后应用NNG算法和OLS算法对空气分离装置中的重要过程参数O2浓度进行了预测。仿真结果表明，NNG算法不仅能对O2浓度进行很好的预测，而且比OLS算法的预测精度更高，模型法更简单，稳定性更好。基于NNG的软测量算法克服了普通传感器价格昂贵、滞后和维护保养困难的缺点，具有较好的实用性和经济性。

[1] 朱学峰. 软测量技术及其应用[J]. 华南理工大学学报(自然科学版), 2002,30(11): 61-67.

[2] 郦晓雪, 肖伯乐. 软测量技术及其在火电厂的应用[J]. 发电设备, 2012,26(1): 62-64.

[3] SUN Kai, LIU Jialin, KANG Jialin, et al. Development of a variable selection method for soft sensor using artificial neural network and nonnegative garrote[J]. Journal of Process Control, 24(2014): 1068-1075.

[4] 谭力宁,韩海涛,马红光. 基于Nonnegative Garrote的ARX和ARMX模型定阶方法[J]. 科学技术与工程,2013,13(9): 2509-2512.

[5] Kesavan P, Lee J H, Saucedo V. Partial least squares(PLS) based Monitoring and control of batch digesters[J]. Journal of Process Control, 2000, 10(23): 229-236.

[6] Breiman L. Better subset regression using the nonnegative garrote [J]. Technometrics,1995, 37: 373-384.

TheApplicationofSoftSensorBasedonNonnegativeGarroteintheAirSeparateProcess

Yu Wang， Sun Kai
(School of Electrical Engineering and Automation, Qilu University of Technology, Jinan 250353, China)

This paper developed a new variable selection method for soft sensor applications using the nonnegative garrote (NNG). This paper took Bayesian information criterion as the model evaluation criterion， and the optimal garrote parameter was determined by v-fold cross-validation. The method were applied to a real industrial application for air separation process. Compared to the least square method, the simulation results showed that the nonnegative garrote has better model accuracy and fewer variables selected.

soft sensor; variable selection; nonnegative garrote

国家自然科学基金项目(61603203)

余旺(1991-),男,济南人,硕士研究生,研究方向:复杂系统建模。

孙凯(1979-),男,鱼台人,副教授,博士,硕士生导师,研究方向:过程控制复杂系统建模。

1007-757X(2017)11-0001-04

TP13

A

2017.04.25)