带有漂浮对象的水波模拟

韩林呈， 陈喜春(机械化步兵学院 作战训练实验中心， 石家庄 050083)

带有漂浮对象的水波模拟

韩林呈， 陈喜春
(机械化步兵学院 作战训练实验中心， 石家庄 050083)

针对实时水波模拟中二维波动方程解法复杂度高、编程求解困难的缺点，基于网格对水面建模，在时间和空间轴上对水波运动离散化处理，并使用数值方法对微分方程近似求解。且为满足场景中水面与物体交互需要，对漂浮对象进行物理建模，通过计算漂浮对象在水中浮力和水波对其推力来模拟水面上的漂浮状态。运行结果表明，该方法可对水波及漂浮物进行实时仿真，模拟速度快，视觉效果好，漂浮效果真实自然。

水波; 物理模型; 波动方程; 离散化; 浮力

0 引言

动态的水可以为室外环境的模拟增加较大的美感，一直是计算机图形学领域研究的重点。作为一种非固定形态的流体，实时地对其进行精确描述较为困难，国内外许多学者均对此有过相关研究。

通常来说，水波模拟主要分为两类：一类方法是基于数学函数模拟绘制水波形状。如文献[1]基于傅立叶合成的方法来模拟海洋波浪；文献[2]采用Perlin噪声源的预计算模拟水面的持续抖动来生成水波效果；文献[3]对文献[1]进行改进，基于逆傅立叶变换生成若干线性函数，将这些函数相互叠加后生成水波；文献[4]将不同相位，不同频率的正弦波的幂函数相互叠加模拟水面波浪；文献[5]受文献[4]启发，但改用余弦的自然指数函数叠加的方法模拟波浪。另一类方法是基于物理模型构建水波。通过求解流体方程，获得流体质点在各个时间的坐标。比较典型的如文献[6]通过解Navies Stokes方程来模拟水面；文献[7]在文献[6]的基础上，采取邻域传播的思想，离散求解Navies Stokes方程，提高了构造水波形状的速度；文献[8]引入物理上用于海水建模的Gerstner波模型对波浪进行构造；文献[9]在充分考虑液体粘性和扩散特性的基础上，基于Lattice Boltzmann流体模型实现了两种液体的混合模拟；文献[10]基于二维波动方程描述水波，使用3D引擎OGRE模拟了水面动态荡漾的效果。

在上述两类方法中，基于数学函数模拟绘制的方法实现简单，在相位、振幅等方面易于控制，但生成的波形规律性较强，不够自然；基于物理方程的方法产生的效果较为真实，但求解复杂、计算量大，实时性较差。为提高求解流体物理方程的效率，本文对水面质点坐标及运动时间分别进行了离散化处理，通过数值方法来近似求解二维波动方程，简化了计算过程，提高了求解速度。此外，大多数学者对水波本身的构成和模拟进行了研究，无论在真实性和实时性上均取得了很好的效果，但对水波与水面漂浮物的互动仿真较少有涉足。本文通过计算物体浮力和水波推力，对物体在水面漂浮滑行的运动过程进行了仿真。

1 二维波动方程

波动方程是一种表示波动现象的偏微分方程，可对自然界的声波、水波等现象进行描述。当水面上无限小的部分移动时，水粒子的直接邻近点会施加线性“弹力”(表面张力)来最小化粒子之间的距离。由于水平方向的力是相等的，粒子仅在z方向运动。关于时间和水粒子空间的位置可以由二维波动方程来描述，如式(1)。

(1)

这里c是波越过水面传播的速度。当边界条件为齐次且水面的初始z方向速度为0时，对于一个L×L大小的正方形水域的通解为式(2)、(3)。

(2)

(3)

系数Amn由计算下面的积分得到式(4)。

(4)

这里f(x,y)是水面的初始形态[11]。如果将水面离散化为以z为高度域且平均分隔的栅格(图1)，则式(4)可以用FFT变换解出[12]。但在实时应用中计算大量的三角函数会大幅降低程序的运行效率。为克服该缺点，本文采用数值方法求近似式(1)。

图1 一个用来近似表示水面的L×L网格，每条边有N个离散点

2 近似求解方法

将流体表面离散化表示为一个顶点排列成表面积为L×L，且每条边含有N个点的规则栅格网络，如图2所示。

图2 计算该点x方向切线斜率

(5)

(6)

(7)

二阶导数可通过计算一阶导数的近似值的方法得出，即计算一阶导数差的平均值来近似求出二阶导数。该点处一阶导数的平均差为式(8)。

(8)

将(5)式代入(8)式得式(9)。

(9)

(10)

可以看出，在某个顶点处二阶导数的计算过程中要用到与该顶点距离两个顶点间距处的顶点位移。将坐标系以(i,j)顶点为中心缩小1/2，同时Δx也缩小1/2，就可以获得对于x的二阶导数的等价近似方程，即式(11)。

(11)

同理可得z相对于y和t的二阶导数近似值为式(12)、(13)。

(12)

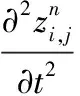
(13)

将式(11)、(12)、(13)代入式(1)，可以得出式(14)。

(14)

(15)

上式说明了点zi,j仅受其相邻点的影响如图3所示。

图3 点zi,j的运动仅受相邻点影响

3 浮力对象

当物体的密度小于水密度时，就可浮于水面之上，物体上的浮力等于其排除的水的重量。该力的方向与气压梯度(pressure gradient)相同，在近似模拟中，可以取水面的法线方向。将船体按照离散的点建模，则其浸入水中的浮力方向，见图4所示。

图4 漂浮物的外形以一组pi近似

(18)

上式中zwater是在pk的双线性差值水面高度。在这个位置的浮力为式(19)。

(19)

且转动力矩为式(20)。

Nk=rkFk

(20)

上式中rk是从质心到pk的矢量。一个对任意参数化的右手螺旋三维表面的法向量可通过式(21)进行计算[13]为式(21)。

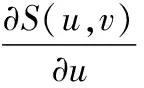
(21)

如果将x和y作为参数，则水面可以用下面的矢量描述为式(22)。

S(x,y)water=[x,y,z(x,y,t)]

(22)

用本文第2节所述方法近似(22)式的导数得式(23)、(24)。

(23)

(24)

则位于第i,j栅格处的法向量为式(25)。

(25)

将该向量放大2h倍，得到等价有效法向量为式(26)。

ni,j=[zi-1,j-zi+1,j,zi,j-1-zi,j+1,2h]

(26)

漂浮物在水面上的推力为漂浮物各点的分力之和为式(27)。

Fdrag=∑-bvk,rel=∑b[vwater-(vcm+ωcm×rk)]

(27)

其中，vk,rel是在rk处漂浮物与水的相对速度，b是相对速度与合力之比。

4 算法实现

4.1 计算z值缓冲区

为实现式(15)所示算法，似乎有必要为在时刻t-1,t0,t1开辟3块内存区域。但是如果zn和zn+1适当代换，则只需要两块内存区域即可。在首次计算结束后，指向zn+1和zn的指针交换。在下一次迭代中，原本指向zn的指针指向了zn+1，而指向zn+1的指针则指向了zn+2。这样只通过两块内存区域就可以实现本文算法。下面是实现该节省内存方法的主要代码。

floatz[N][N];//z^n值

floatz1[N][N];//z^(n-1)和z^(n+1)值

floatu[N][N];//粘性阻力

floatd[N][N];//阻尼系数

…

const floatA= (c*dt/h)*(c*dt/h);

const floatB= 2 - 4*A;

longi,j;

for(i=1 ;ilt;N-1 ;i++ )

{

for(j=1 ;jlt;N-1 ;j++ )

{

u[i][j] =z1[i][j];

//以z^(n-1)和z^n更新z^(n+1)

z1[i][j] =A*(z[i-1][j] +z[i+1][j] +z[i][j-1] +z[i][j+1] )+B*z[i][j] -z1[i][j];

u[i][j] = (z1[i][j]-u[i][j])/2t;//计算粘性阻力

z1[i][j] -=u[i][j]; //应用粘性阻力

//z1[i][j] *=d[i][j]; //或者应用阻尼系数

}

}

//交换z^n和z^(n+1)

swap(z,z1 );

4.2 增加波源

为了形成水波，需在水中加入波源。程序运行初始，在某点增加该位置的z值，则波浪以该点为中心形成。以下是增加波源的主要代码。

const longN= 128 + 1;//N为水面边界的离散点数目

…

z[N/3][N/3] =z1[N/3][N/3] = 10; //创建波浪

5 测试

在CPU为i7-5500 2.40GHz，显卡为AMD Radeon R5，内存4GB，32位Win7系统下，基于C++和OPENGL3.2对本文算法进行编程测试，效果如图5-图12所示。

图5 网格水平面

图6 创建水波，波浪从该点发出

图7 水波开始扩散

图8 物体漂浮在水面

图9 水波推动漂浮物体滑行

图10 加入光照及进行渲染后效果1

图11 加入光照及进行渲染后效果2

图12 加入光照及进行渲染后效果3

在程序开始运行时，首先初始化所有的z值为0，即处于一个平静的水平面(图5)。然后选取任一点，设置一个较大的z值，从该点开始进行扩散(图6、7)。该点的z值决定了一开始水波波动的高度。图8、图9为物体漂浮及在受水波推动滑行的效果。图10-12为加入光照并进行渲染后的效果图。文中场景均为128×128个网格，刷新率达到59帧/秒，运行流畅。

7 总结

本文基于二维波动方程，采用数值方法对该物理方程快速求解，同时对水面漂浮物所受浮力和推力进行计算，最后基于OPENGL对水面的波动效果和与漂浮物的交互效果进行了模拟。该方法程序设计简单，计算量小，运算速度快，对漂浮物体的仿真效果真实感较强。但通过本文算法实现的水波还是较为规则，与真实自然环境中多变的情况仍有差距。在下一步工作中，还将参考更多流体物理方程(如N-S方程)的引入，并加入随机因素及其他水面特效(如浪花)等。

[1] MASTIN G A，WATTERBERG P A，MAREDA J F．Fourier synthesis of ocean scenes[J]．IEEE Computer Graphics amp; Applications, 1987, 7(3): 16-23.

[2] Hugo Elias. Perlin noise [EB/OL]. http://free space.virgin.net/hugo.elias/models/m_perlin.htm.

[3] 聂卫东, 康凤举, 褚彦军, 等. 基于线性海浪理论的海浪数值模拟[J]. 系统仿真学报, 2005, 5(17): 1037-1044.

[4] 方建文, 于金辉, 马文龙. 图形硬件加速的实时水面绘制[J]. 计算机工程与应用, 2006, 42(15): 86-88.

[5] 刘晓平, 谢文军. 实时水面模拟方法研究[J]. 工程图学学, 2010, 1: 79-83.

[6] FOSTER N, M ETEXAS D. Realistic animation of liquids [J]． Graphical Models and Image Processing, 1996, 58(5): 471-483.

[7] 吴献, 董兰芳, 卢德唐. 一种基于邻域传播的水波模拟方法[J]. 中国科技大学学报, 2010, 40(3): 278-282.

[8] 王海玲, 印桂生, 张菁, 等. 基于改进曲面熵的动态水面模拟方法[J]. 计算机工程, 2011, 37(6): 24-26.

[9] 朱红斌，刘学慧，柳有权，等．基于Lattice Boltzmann模型的液-液混合流模拟[J]． 计算机学报, 2006, 29(12): 2071-2079.

[10] 孙晓鹏, 李翠芳. 三维游戏中基于OGRE的动态水面模拟算法[J]. 计算机工程与设计, 2011, 32(12):4122-4124.

[11] Trim D W. Applied Partial Differential Equations[M]. PWS-Kent, 1990.

[12] William H, Teukolsky Saul A, Vetterling,etal. Numerical Recipes in C (second edition)[M]. Cambridge. The Press Syndicate of the University of Cambridge, 1992.

[13] Davis, Harry F., Snider, Arthur David, Introduction to Vector Analysis (sixth edition)[M]. William C. Brown Publishers, 1991.

WaveSimulationwithaFloatingObject

Han Lincheng, Chen Xichun
(Combat Training Experiment Center, Mechanized Infantry Academy, Shijiazhuang 050083)

For the high complexity and programming difficulty in solving 2-dimensional wave equation in real-time wave simulation, a model is bullt based on water face grid, the wave motion is olescreted in time and space axis, and numerical methods are used to solv differential equation. In order to meet the need of the interaction between the surface and the object in the scene, the floating object is modeled by the physical modeling, and the floating state of the object is simulated by calculating the buoyancy and thrust. The results show that the method can simulate the wave and floating object in real time, the simulation speed is fast, the visual result is good, and the floating effect is real and natural.

Wave; Physical modeling; Wave equation; Discrete; Buoyancy

韩林呈(1984-)，男，石家庄市人，硕士，讲师，研究方向为计算机图形学。

1007-757X(2017)11-0069-05

TP391

A

2016.10.29)