二级倒立摆的T-S模糊控制器设计

李志刚，吴楠

(1.华北理工大学 信息工程学院，河北 唐山063210；2.华北理工大学 电气工程学院，河北 唐山 063210)

二级倒立摆的T-S模糊控制器设计

李志刚1，吴楠2

(1.华北理工大学 信息工程学院，河北 唐山063210；2.华北理工大学 电气工程学院，河北 唐山 063210)

二级倒立摆；T-S模糊控制器；融合函数；遗传算法

为了解决多变量、非线性、强耦合的二级倒立摆系统在进行模糊控制时遇到的模糊规则爆炸问题，设计了基于融合变量的T-S模糊控制器。通过配置极点设计融合函数，以融合函数生成的变量作为输入，倒立摆控制输入为T-S模糊控制器输出；采用改进遗传算法对T-S模糊控制器进行鲁棒性优化。仿真实验表明，所设计的二级倒立摆的T-S模糊控制器鲁棒性比较好。

任何理论的研究都是为了适应现实的需要，对于一个典型的非线性、高阶次、多变量、强耦合、不稳定的倒立摆系统来说，它的理论研究具有很重要的工业、军事和经济背景[1]。近年来，国内外对二级倒立摆系统不仅体现在起摆控制研究，而且在稳定性控制这方面的研究也已成为热点。倒立摆的稳定性的有效控制方法也应用在很多方面，比如双足机器人的行走、火箭发射中的垂直控制度及海上钻井平台的稳定控制[2]。

该项设计基于变量融合的T-S模糊控制系统，首先运用牛顿第二定律建立数学模型，再通过配置极点设计融合函数，以融合函数生成的变量作为T-S模糊控制器的输入，二级倒立摆控制输入作为T-S模糊控制器输出；在运用改进遗传算法对T-S模糊控制的配置极点进行优化，从而为解决多变量模糊控制器设计中的"模糊爆炸"问题提供一种新方法。

1 二级倒立摆系统建模

二级倒立摆受力分析图如图1所示。

图1 二级倒立摆受力分析图

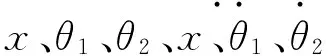
图2所示为下摆杆受力分析图，图3所示为上摆杆受力分析图。

图2 下摆杆受力分析图 图3 上摆杆受力分析图

对二级倒立摆数学模型建立，用牛顿第二定律建立系统的动力学方程[3]：

(1)对二级倒立摆整个系统图1分析，在水平方向有：

(1)

(2)图2对下摆杆受力分析，其方程为：

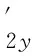
(2)

(3)图3对上摆杆受力分析：

(3)

对(1)、(2)、(3)式进行整理分析，可得二级倒立摆系统的动力学方程：

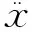
(4)

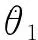
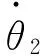
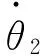
(5)

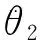
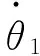
(6)

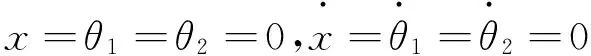
2 变量融合的T-S模糊控制器

模糊控制在设计系统时与传统的控制相比不需要建立被控对象，模糊控制推理输出是输入量的函数，不需要经过清晰化处理，可以逼近任意非线性系统，适用于局部线性、多变量、能够分段进行控制的系统，方便于对它进行数学分析。在实际的控制系统中，T-S模糊控制系统可描述为[4]：

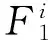
(7)

其中，x=[x1(t)]为模糊系统的状态向量。模糊控制系统总体模型为：

(8)

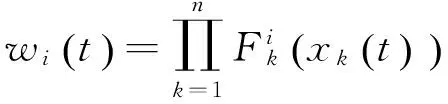
二级倒立摆系统共有6个变量，设每个变量有7个模糊集，若将每个变量作为T-S模糊控制器的输入，共有117 649条模糊控制规则，将出现“模糊规则爆炸”的问题。为了解决模糊规则爆炸问题，该项目采取了变量融合方法，通过将6个变量合成2个变量作为T-S模糊控制器的输入，不仅减少模糊控制器的控制规则，还保持了模糊控制器实际简单快速的优点。设融合函数为

(9)

通过融合函数F(X)将二级倒立摆的小车位移与两根摆杆角度融合为E，小车速度与两根摆杆角速度的融合为EC，这样达到对实际状态变量的降维，变量融合为

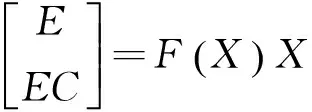
(10)

则式(7)可变为：

则所设计T-S模糊控制器的输入变量从6维输入变量降低为2维，降低了设计难度，提高了T-S模糊控制器的运行效率。图4为融合设计过程图：

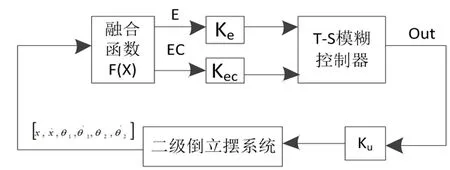
图4 二级倒立摆融合示意图

3 基于遗传算法的T-S模糊控制器的设计

模糊控制器的设计包括控制器结构的设计、语言变量的设计、精确量的模糊化、建立控制规则、输出信息的模糊判决以及模糊控制查询表的建立[5]。该项目通过设计改进遗传算法来优化T-S模糊控制器规则，减少了模糊控制器的输入变量，从而使模糊控制器的构造和设计变得更加的清楚明了。该项设计通过控制规则找到极点配置中的反馈矩阵K，6个变量可以划分为7个模糊子集，T-S模糊控制器的控制规则即用两个输入变量：E和EC，每个输入变量有7个语言值(NB, NM, NS, O, PS, PM, PB)，这样所确定优化的初始种群模糊控制规则条数为49条，这49条控制规则是按照2个输入变量顺序进行排列组合，来保证其覆盖整个输入空间。具体设计步骤如下：

步骤1：确定T-S模糊控制器的输入量、输出量及语言变量的隶属度值等基本参数；

步骤2：设计生成初始种群。初始种群各个局部线性控制器的极点，运用极点配置方法设计出各个局部线性控制器；

步骤3：利用改进遗传算法，对各个局部线性控制器的反馈控制极点进行优化，求得最优的T-S模糊控制器。

3.1 适应度函数

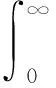
根据二级倒立摆控制器的特点，该项设计在选取适应度函数以二级倒立摆的的输出位移误差、输出角度误差及模糊控制器的输出控制量作为参考指标，这样不仅保证二级倒立摆达到稳态所需要的时间较少，又保证二级倒立摆在控制过程中的振荡幅度较小。如(11)式所示：

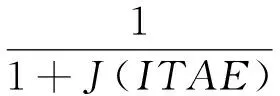
(11)

3.2 初始种群产生

初始种群是遗传算法迭代运算的开端，为了保证初始种群中的染色体为有效染色体，所以改进遗传算法的初始种群中的染色体不再随机产生，随机设置二级倒立摆的初始状态，优化其反馈控制极点参数，并将T-S模糊控制器中的各个局部控制器的反馈控制极点设置为优化得到的反馈控制器的反馈控制极点。每个染色体98组数依次排列组成，依次代表98组局部控制器的反馈控制极点参数，均为优化得到的反馈控制器的反馈控制极点参数。这样不仅保证了98条染色体的收敛性，也保证了初始种群的多样性。

优化二级倒立摆反馈控制极点的遗传算法与改进的遗传算法的初始种群的产生不同，而其他的遗传算子及适应度函数则相同。优化二级倒立摆反馈控制极点只优化一个反馈控制器，根据二级倒立摆的初始状态等优化6个极点，分别代表一个反馈控制器的配置极点的共轭极点的实部、阻尼系数和其它4个极点与共轭极点的实部绝对值的比值。通过优化6+2*49个参数来得到6个反馈矩阵也就是极点配置中的6个状态反馈矩阵。随机产生100个初始状态，并运用上述改进遗传算法得到优化结果，为了提高种群的优化效率，保证解空间的全面性，所以初始种群染色体中各个染色体个数均为1。

3.3 改进遗传算法

与基本遗传算法相比，该项设计的主要改进体现在2个方面：一是最优保留策略[6]，二是多种群优化策略。最优保留策略的主要步骤是，进行遗传算子计算之前记录上一代最优个体，若上一代最优个体适应度值大于此代最优个体，则将上一代最优个体代替此代的适应度最低的个体。否则，直接进入下一代计算。多种群优化策略是指将种群分为多个子种群，子种群分别进行独立的遗传优化。遗传优化进行到固定的代数，将各个子种群之间进行一定量的染色体交换，可有效解决遗传算法的早熟问题。首先，初始种群不再随机产生，而是按照初始种群确定的状态进行，以提高染色体在有效空间内出现的频率；然后，在遗传算法中加入种群算子能够更好地维持种群多样性，提高优化效率。改进遗传算法优化流程图如图5所示：

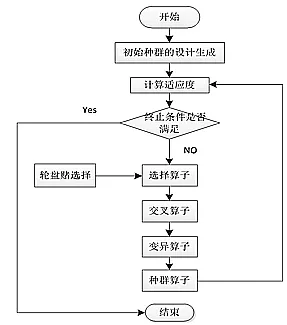
图5 改进遗传算法优化流程图

4 实验仿真分析

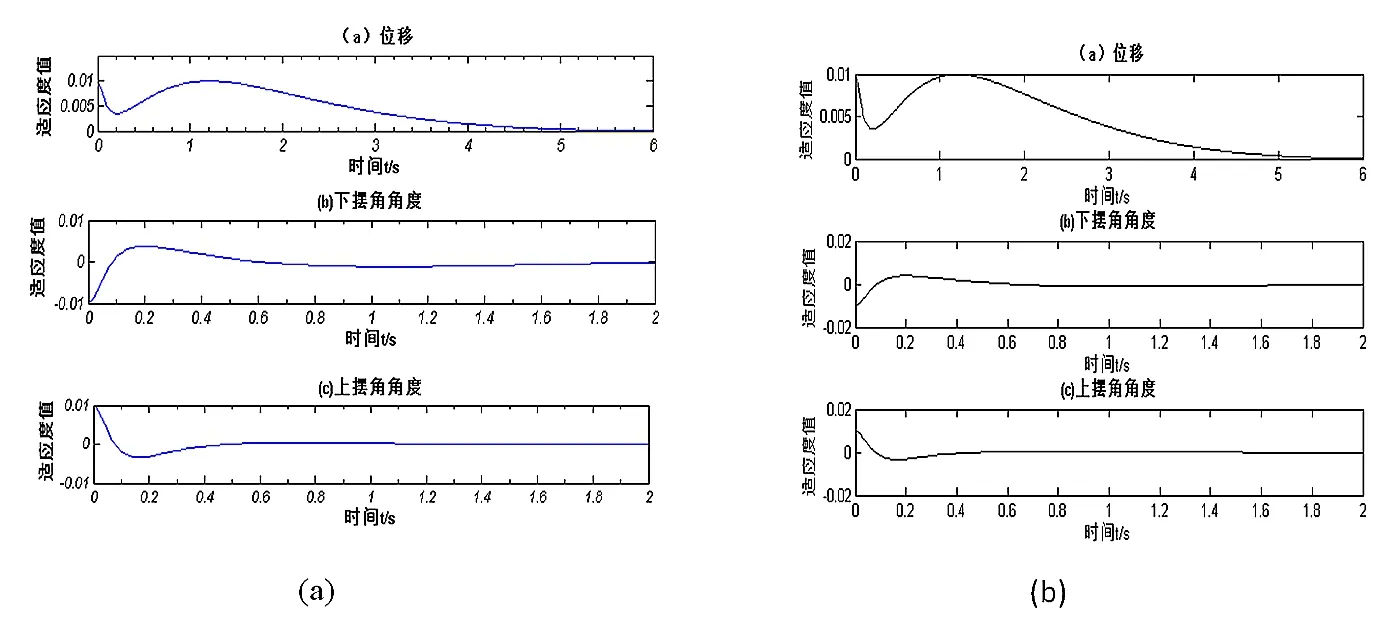
图6 二级倒立摆控制曲线仿真图

5 结论

该项目以二级倒立摆为被控对象设计了T-S模糊控制器，利用融合变量对T-S模糊控制器的输入进行降维，解决了多输入变量遇到的“规则爆炸”问题，通过改进的遗传算法优化T-S模糊控制器的方法具有一定的可行性，可使二级倒立摆控制曲线能够在短时间内快速达到很好的控制效果，鲁棒性好。因此，该项目提出的设计方法对其它多变量，不稳定系统也有一定的参加价值。

[1] 韩复健.倒立摆系统的发展研究以及意义[J].山东工业技术,2014,17(154):144-145.

[2] 邵瑞. 基于滑模观测器的环形倒立摆控制系统的设计与实现[D].株洲:湖南工业大学,2011.

[3] 岳春然.基于模糊控制算法的倒立摆系统的研究[D]:北京:北方工业大学,2009.

[4] 刘玉琳.基于T-S模糊系统的稳定性分析及控制器设计[D].大庆:东北石油大学,2013.

[5] 茅晓辉.风力发电机变浆距控制策略研究[J].山东科技大学,2014,22(10):16-18.

[6] 张雅舰,刘勇,谢松江. 一种求解装箱问题的改进遗传算法[J].控制工程,2016,3(12):329-331.

DesignofT-SFuzzyControllerofDoubleInvertedPendulum

LI Zhi-gang1, WU Nan2

(1. College of Information Engineering, North China University of Science and Technology, Tangshan Hebei 063210, China;2. College of Electrical Engineering, North China University of Science and Technology, Tangshan Hebei 063210, China)

double inverted pendulum; T-S fuzzy controller; fusion function; genetic algorithm

In order to solve the multivariable, nonlinear and strong-coupling of the double inverted pendulum system with the fuzzy rules explosion problem, a T-S fuzzy controller based on the fusion function was designed. The fusion function was designed with the pole design. The T-S fuzzy controller is input by using the variable generated by the fusion function, and the output by the inverted pendulum control input. The improved genetic algorithm is used to optimize the robustness of the T-S fuzzy controller.The simulation results show that the design of the double inverted pendulum T-S fuzzy controller robustness is better.

2095-2716(2017)04-0082-06

2017-05-24

2017-09-25

河北省自然科学基金资助项目(F2013209203)。

TP242.6

A