“问题导向式”教学法在高职数学教学中的探索——以微积分教学为例

李 姣 娜

(重庆电子工程职业学院 马克思与通识教育学院, 重庆 401331)

“问题导向式”教学法在高职数学教学中的探索
——以微积分教学为例

李 姣 娜

(重庆电子工程职业学院 马克思与通识教育学院, 重庆 401331)

针对高职院校高等数学微积分模块教学的现状，探讨了“问题导向式”教学法在教学中的实施，通过问题设计让学生参与到课堂教学中，引导学生逐步认识问题的本源及所学知识的核心，促进教学的互动效应和应用数学的意识，提高教学效果。

问题导向式；教学法；微积分

引言

“高等数学”这门课程是高职院校多个专业的理论基石，特别是对于理工科的专业学习尤为重要。而该学科知识较为抽象、理论性和逻辑性较强，再加上高职学生数学基础相对薄弱，学习兴趣不浓，自制力差，这些都成为大多数高职学生学好这门课程的绊脚石。如何激发学生的学习兴趣，调动学生的积极性，学好并会运用所学数学知识解决实际问题，成为广大数学教师一直忧虑的问题[1]。在当前课改模式下，“问题导向式”教学方法得到了广泛的关注和应用，它是以“问题”为主线，激发学生的好奇心和求知欲，引导学生追寻问题本源，深入研究问题，自主探索。国内众多教育工作者也将其运用到各自的教学领域，雷蕾[2]将其应用到西方经济学的课堂教学中，张应红等[3]将其应用到材料力学实验教学中，崔义成等[4,5]在论文中阐述了将问题导向教学模式应用到高校思想政治课的教学探索。笔者在微积分的教学中也大胆尝试了该教学方法。

1 “问题导向式”教学法

“问题导向式”教学法是基于行动导向并在工作过程导向系统理论指导下，以问题为驱动力和以培养学习者问题意识、批判性的思维技巧以及解决问题的实践能力为主要目标的一种教学方法。该教学方法在1969年由美国Barrow教授在加拿大麦克马斯特大学(McMaster University )提出，并在1993年爱丁堡医学教育高峰论坛中得到推荐[6]。目前已成为国内外十分流行的教学模式，被广泛应用于医学、数学、教育、经济、法律等学科。

“问题导向式”课堂教学活动通过教师精心设计问题，引人入胜地提出问题，从而引导学生动手解决问题。将传统教学中学生的被动状态转变为主动的“激活”状态。整个课堂是一个不断提问题的过程，教学内容由环环相扣的问题组成，教者要思路清晰，教学内容明确，重难点把握适当。同时要掌握好提出问题、分析问题、解决问题这三个环节的节奏。所围绕的关键是——问题，问题是数学发展的原始驱动力，由于数学研究是由问题驱动的，数学学习要模拟数学研究的过程[7]，因此问题的设置在整个教学过程中更是起到决定性的作用。

1.1 问题的有效性

课堂上，毫无准备和不假思索地随便将问题盲目抛出、不给学生思考时间就加以提问、或者只问不答都不是有效的做法。导入问题、提出问题必须把握针对性和有效性，温故知新中的“故”一定要和“新”相关，在问题的选择上要遵循教学目标的要求，提出的问题既不能太直白也不能太深奥，既不能过于机械也不能天马行空，要恰到好处，又留有悬念。要紧扣教学的重难点，使得所设的问题能够最大程度的有益于教学。

1.2 问题的明确性

如果盲目地将问题抛给学生，所设问题没有针对具体的知识和要解决的问题，没有考虑学生的认知水平和认知规律，致使学生在解决问题时寸步难行，这都说明所设问题不明确，从而降低了教学效果。有些问题的导入要循序渐进，只有教者思路明确，可以根据瞬息万变的课堂气氛来调动学生的探究兴趣，随学而教，避免盲目排除导致问题无效。

1.3 问题的创新性

若问题过于呆板、机械，学生只是回答“是”或者“不是”，教学就收不到良好效果。教者可以对问题的形式和内容加以“包装”，使学生在思考时不会感到枯燥、乏味。同时，新颖的问题可以对感官和神经加以刺激，激发学生的好奇心和求知欲。

1.4 问题的生活性

著名教育家杜威曾说：“教育即生活，即生长，即经验改造。”好的教学始终是从生活中来，到生活中去的。数学家波利亚曾说“数学教师的责任是尽其可能来发展学生解决问题的能力”。所设问题尽量要贴近生活、充分利用学生已有的生活经验和阅历，引导学生将数学知识运用到实际生活中去，充分体会数学在现实世界的应用价值。

2 “问题导向式”教学法在微积分教学中的具体实施

微积分是高等数学理论的重要内容，它贯穿于整个知识结构的始终。对于高职院校的老师，在教学中要力求将枯燥的概念深入浅出、形象生动的表达，重视数学概念的本质，不拘限于形式。对复杂的定理、结论、方法的综合与叙述，能以通俗易懂的描述、直观地说明方法替代一切繁琐的推理。在不刻意追求数学学科的系统性和严谨性的基础上，尽力体现降低理论、保证基础、加强应用、突出工具作用。

2.1 抓住问题本源，构建模型

本源性数学问题旨在数学教学中把某个数学问题的“要素”或“基本构成”作为思考的第一问题。抓住问题的本源，即揭开了挡在问题前面的层层面纱，问题自然迎刃而解。

例题1：某人在限速为 100km/h的公路上行驶，监控仪记录了他在20分钟内行驶了40km，那么，警察是否会给他开出一张罚单？

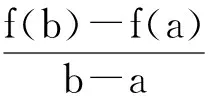
2.2 深入研究问题，自主探究

问题是教学的源泉，也是学生自主探究学习的动力，它既能给学生提供探究和发现的体验，又有助于培养学生的问题意识和创新意识。数学课堂中，教师要不断提出问题，环环相扣，引导学生自主探究，激活原有的知识，理解同化、迁移，大胆猜想，加以论证，再生成新知识，进而有效实现教学预设。

例题2：某水库因为地势原因将闸门设计为圆形，其半径为R，当水面与闸门直径相齐时(如图1)，那么水对闸门一侧的压力有多大？学生读懂题意后，便可归纳出这是一个力学问题。

首先提出问题1：压力公式是什么？

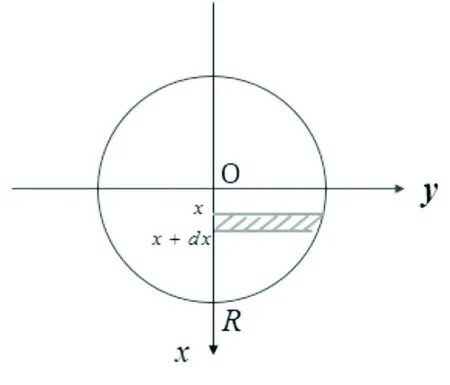
图1 闸门受力示意图

具有初等力学知识的学生便会解答出，压力等于压强乘以受力面积，即F=PS=ρgxπx2，其中，P是压强，S是受力面积，ρ是水的密度，g是重力加速度，x是半径。

进一步提出问题2：压力在闸门上是均匀分布的吗？

经过思考，有学生会指出不是均匀分布。

再进一步提出问题3：刚才大家给出的压力表达式能否准确表达闸门一侧的压力？

学生回答不能，同时还继续思考和讨论该用什么方法解决上述问题。

此时，引出所授知识点——微元法。例题2中，力在闸门上不均匀的主要原因是，不同的水深压强不同，且相同的深度差，受力面积也不同。因此，可以先把整体量(深度)进行分割，然后在局部范围内“以直代曲”，求出整体量在局部的近似值，再累加，无限细分，最后取极限。

给学生一定的思考时间，有同学提出，这个过程好像前面讲的定积分。

事实上，许多几何量和物理量都可以用这种方法计算。上述例题2，适当的建立直角坐标系，以水深为自变量，所求的压力就是计算区间上某个量的定积分。接下来逐步引导学生解决问题：

第一：选取x为积分变量，积分区间为[0,R]；

第二:在区间[0,R]上任取一小区间[x,x+dx]，由于对称性，面积元素为：

(1)

对这一小薄片所受的压强P近似看作不变，压力元素为：dF=Pds

由于水深处的压强 ，将该式与(1)式代入得

(2)

其中，ρ是水的密度，g是重力加速度.

第三：变量x在区间 [0,R]上积分，就得到水对闸门一侧的压力

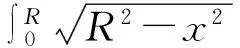
问题解决至此，学生已经在讨论对比前后两种方法的差异了。接下来，进一步引导学生总结微元法的应用。

3 结语

在“问题导向式”教学中，教师要担当引导的角色，这就要求教师明确教学目的，有效提出问题，把握课堂节奏，步步为营，有计划地实现教学预设。实践证明，在高等数学教学中，适当的运用“问题导向式”教学方法，有助于激发学生的主动精神，提高学生的创新思维能力，有利于构建以学生为主体的课堂教学环境。

[1] 郑君文，张恩华.数学学习论[M]. 南宁：广西教育出版社，1996.

[2] 雷蕾.问题导向式教学法在课堂教学中的应用[J].重庆科技学院学报:社会科学版，2010,(11):196-197.

[3] 张应红，景晖，孙永厚，等.问题导向式教学法在材料力学实验中的实践与探索[J].实验室科学，2014,17(4):132-134.

[4] 崔义成，施复兴，祝移民.问题导向教学模式的应用研究(一)[J].湖北工业职业技术学院学报，2014，27(2):81-86.

[5] 崔义成，张西平，徐瑛，等.问题导向教学模式的理论与实践再探索[J].十堰职业技术学院学报，2013，26(6)：91-95.

[6] Schmidt H G, Rotgans J I, Yew E H J. The process of problem -based learning: what works and why. Medical education[J]. 2011,45(8):792-806.

[7] 张玉灵，冯改红.在高等数学中尝试“问题驱动”教学模式[J].成都师范学院学报，2013，29(3):110-112.

(责任编辑：刘小林)

10.3969/j.issn.1009-2080.2017.06.018

G712

A

1009-2080(2017)06-0096-03

2017-10-08

李姣娜(1983-)，女，黑龙江绥化人，重庆电子工程职业学院讲师，硕士。