巧用三大工具破解二次函数难点

苗鑫

巧用三大工具破解二次函数难点

苗鑫

二次函数是初中数学的重点内容，也是各地中考考查的一个热点.需要同学们熟练地掌握它的基本性质，并能灵活应用.本文就同学们学习本单元过程中的典型问题，借助“画图”“分类”“转化”等方法，帮助同学们解决学习中的实际困难.

一、借助二次函数图像解题

无论是哪一种函数，我们都是通过图像去研究它的性质，然而在同学们的学习过程中，函数图像是最被忽视的一个内容.画二次函数图像不仅是研究二次函数性质的工具，也是解决许多数学问题的重要方法.熟练应用这一工具可以帮助同学们在学习中获得逻辑推理、数形结合等思想方法，从而为进一步学习奠定基础.

1.利用二次函数图像判断有关系数及代数式的符号.

例1已知二次函数y=ax2+bx+c（a≠0）的图像如图1所示，则下列结论：①ac＞0；②方程ax2+bx+c=0的两根之和大于0；③y随x的增大而增大；④a+b+c＜0，其中正确的个数是（）.

A.4个B.3个C.2个D.1个

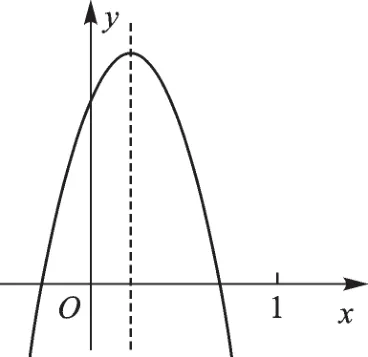
图1

【解析】由图像得a＜0，c＞0，所以ac＞0不成立；由于对称轴在y轴的右侧，所以-＞0，又a＜0，所以b＞0，所以方程ax2+bx+c=0的两根之和大于0成立；y随x的增大而增大不一定成立；由图像可知当x=1时，y＜0，即a+b+c＜0正确.故选C.

【点评】本题考查了同学们数形结合能力和创新应用能力.

2.不求函数解析式，利用图像对称性解方程.

例2若二次函数y=-x2+2x+k的部分图像如图2，则关于x的一元二次方程-x2+2x+k=0的一个解x1=3，另一个解x2=

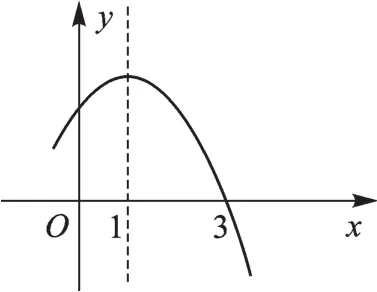
图2

【解析】本题可根据抛物线的对称性求得x2=-1，也可以用对称轴的两点公式求，即x=

3.利用二次函数图像的平移规律解题.

例3抛物线y=3x2+2x-1向上平移4个单位长度后的函数解析式为（）.

A.y=3x2+2x-5B.y=3x2+2x-4

C.y=3x2+2x+3D.y=3x2+2x+4

【解析】利用平移规律“上加下减”，抛物线y=3x2+2x-1向上平移4个单位长度，解析式中常数项加4，所以是y=3x2+2x-1+4=3x2+2x+3，故选C.

【点评】本题考查了二次函数图像与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式.

二、巧用“分类”工具解题

1.在不确定函救的类型时，要分类讨论.

例4若函数y=（a-1）x2-4x+2a的图像与x轴有且只有一个交点，则a的值为

【解析】∵函数y=（a-1）x2-4x+2a的图像与x轴有且只有一个交点，∴当函数为二次函数时，Δ=16-4（a-1）×2a=0，解得：a1=-1，a2=2；当函数为一次函数时，a-1=0，解得：a=1.

故答案为：-1或2或1.

【点评】实际上题设中未说明函数的类型，因此所给函数可以是二次函数，也可以是一次函数.

2.根据函数的自变量范围分类讨论解题.

例5已知二次函数y=（x-h）2+1（h为常数），在自变量x的值满足1≤x≤3的情况下，与其对应的函数值y的最小值为5，则h的值为（）.

A.1或-5B.-1或5C.1或-3D.1或3

【解析】∵当x＞h时，y随x的增大而增大，当x＜h时，y随x的增大而减小，

∴①若h＜1≤x≤3，当x=1时，y取得最小值5，可得：（1-h）2+1=5，解得：h=-1或h=3（舍）；

②若1≤x≤3＜h，当x=3时，y取得最小值5，可得：（3-h）2+1=5，解得：h=5或h=1（舍）.

综上，h的值为-1或5，故选：B.

【点评】本题主要考查二次函数的性质和最值，根据二次函数的性质和最值分类讨论是解题的关键.

三、灵活“转化”破难点

1.根据二次函数与方程、不等式三者关系，互相转化解题.

例6二次函数y=ax2+bx+c（a≠0）的部分图像如图3所示，对称轴为直线x=-1，与x轴的一个交点为（1，0），与y轴的交点为（0，3），则方程ax2+bx+c=0（a≠0）的解为（）.

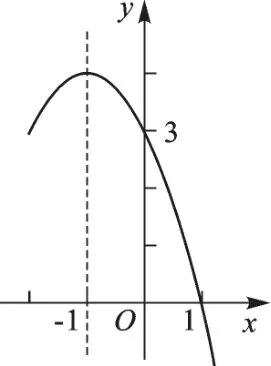
图3

A.x=1B.x=-1

C.1或-3D.1或-4

【解析】由对称轴为直线x=-1及一个交点（1，0）可求出另一个与x轴的交点坐标为（-3，0），选C.

【点评】本题考查的是二次函数图像的性质.方程ax2+bx+c=0（a≠0）的解的实质是当二次函数值为0时其图像与x轴的交点的横坐标.同学们可以利用转化思想求不等式ax2+bx+c＜0的解集.

2.利用二次函数三种解析式的互相变换解题.

例7在平面直角坐标系xOy中，抛物线y=mx2-2mx+m-1（m＞0）与x轴的交点为A，B.横、纵坐标都是整数的点叫作整点.若抛物线在点A，B之间的部分与线段AB所围成的区域内（包括边界）恰有6个整点，求m的取值范围.

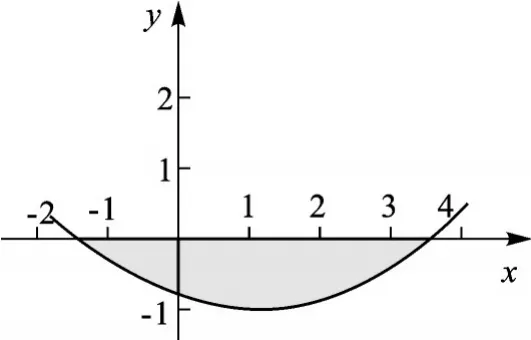
图4

【解析】抛物线y=mx2-2mx+m-1（m＞0）=m（x-1）2-1，抛物线顶点为（1，-1），则题干中所需的整点的纵坐标只能为-1或者0，所以要求AB线段上（含AB两点）必须有5个整点.令y=mx2-2mx+m-1=0，得到A、B两点坐标分别为，即5个整点是以（1，0）为中心向两侧分散，进而得到

【点评】在遇到二次函数解析式问题时，要注意选取适当形式，或根据需要变形是快速解题的重要办法.

（作者单位：江苏省宿迁市湖滨新区实验中学）