四旋翼无人飞行器控制算法设计

赵 玥，陈奕梅

天津工业大学 电气工程与自动化学院，天津 300387

四旋翼无人飞行器控制算法设计

赵 玥，陈奕梅

天津工业大学 电气工程与自动化学院，天津 300387

针对Qball-X4四旋翼无人飞行器的自身特点，建立系统的非线性模型，采用姿态内环和位置外环的双闭环控制算法。线性二次型调节器（LQR）可以快速简便地求解出最优的状态反馈控制率，并且具有良好的鲁棒性，因而利用LQR控制算法来控制姿态内环。由于PID控制算法结构简单、鲁棒性强，因而控制位置外环。通过Matlab/Simulink和飞行试验对控制算法进行仿真和验证，结果表明，设计的控制算法能成功地实现飞行器的悬停控制，并达到较好的控制效果。

四旋翼无人飞行器；非线性模型；线性二次型调节器；PID控制算法

1 引言

四旋翼无人飞行器是一种微小型飞行器，能够进行自主悬停，前飞、侧飞、倒飞等动作，具有性能优良、体积小、飞行速度快、续航能力强等许多特点[1]，因此，被广泛用于军事侦察、航拍、搜索、紧急救援、情报获取等任务，具有很好的实际应用性和发展前景。由于无人机在国防、民用、商用等方面的巨大价值，已经成为控制方面研究的热点[2]。

四旋翼无人飞行器是典型的非线性系统，具有多变量，欠驱动，强耦合等特点。针对飞行器控制算法问题，国内外高校和研究机构都进行了许多研究[3]。早期，在研究此类问题时，都将无人机模型线性化，运用经典线性控制理论解决此类问题，例如：PID控制算法[4]，LQR控制算法[5]等。之后，为了解决不确定的外部干扰以及模型的不精确，又将滑模控制算法[6]，自抗扰控制算法[7]等应用在飞行器中。但是由于实际系统的复杂性，大多数研究也仅限于仿真，并没有在实际系统中进行验证。

本文针对Quanser公司生产的Qball-X4四旋翼飞行器试验平台，考虑到实际飞行中的各种不确定情况，设计了双闭环的四旋翼无人飞行器的控制算法，并应用到实际平台中，实现了室内的悬停飞行试验。控制算法分为两部分，内环采用LQR控制算法，外环采用PID控制算法。这种控制算法结构简单、鲁棒性强、可靠性高，并且试验结果验证控制方法是有效的，因此可以将此方法应用于飞行器实际控制中[8]。

2 动力学建模

四旋翼飞行器呈十字交叉结构，四个驱动电机对称安装在十字结构末端，通过调节四个电机的转速完成飞行器的飞行控制。1，3号电机顺时针旋转，2，4号电机逆时针旋转。Fi是第i个电机产生的升力（i=1，2，3，4），在机体坐标系下，定义飞行器绕Y轴旋转产生的角度为φ滚转角（Roll），定义绕X轴旋转产生的角度为θ俯仰角（Pitch），定义绕Z轴旋转产生的角度为φ偏航角（Yaw）。图1为Qball-X4的实物模型和动力学建模示意图。

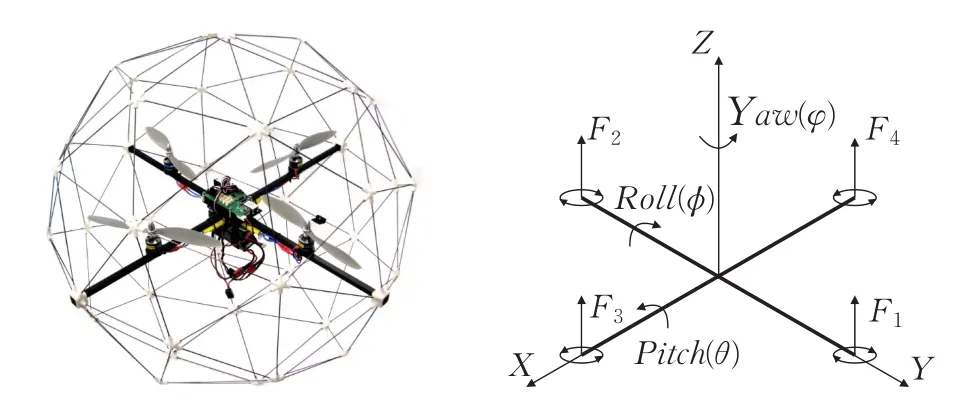
图1 四旋翼飞行器实物图与动力学建模示意图

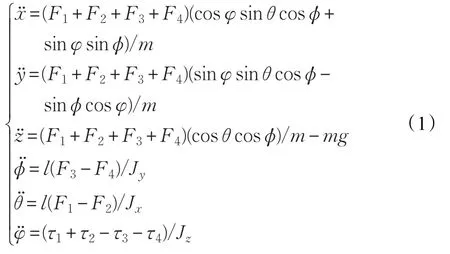
考虑到实际飞行的特点，在慢速飞行下，忽略空气阻力且飞行器旋翼没有弹性形变及认定其为刚体的情况下，对飞行器进行建模，其数学模型如下[9]：其中，(x,y,z)是指飞行器相对于地面坐标系原点的位置，m是指飞行器质量，g是指重力加速度，l是指飞行器坐标系中心到旋翼中心的长度，(Jx,Jy,Jz)是指飞行器绕机体坐标系X轴Y轴Z轴旋转的转动惯量，τi是指第i个旋翼产生的偏转扭矩。

由电机参数可知，飞行器每个旋翼产生的升力和电机的PWM输入满足以下关系[10]：

其中，ui是指第i个电机的PWM输入，K是指正增益系数，ω是指带宽。

四个旋翼产生的扭矩和电机PWM之间的关系可近似为：

为了便于设计控制量，定义虚拟控制量U1=u1+u2+u3+u4，U2=u3-u4，U3=u1-u2，U4=u1+u2-u3-u4。根据以上条件，将飞行器模型简化为：

观察比较2组患者手术时间，术后引流时间及术中出血量，术后3 d、5 d及7 d患者VAS评分，术后并发症，患者治疗满意率。随访1年，观察2组患者复发情况。VAS评分[9]：评估患者疼痛程度，评分范围0～10分，分值越高表示患者疼痛越严重。

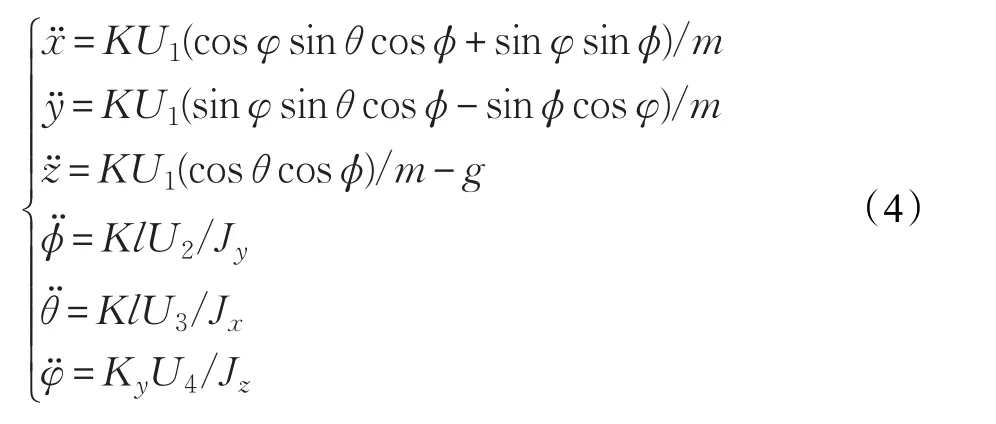
3 控制算法设计

四旋翼飞行器是典型的欠驱动系统，在控制过程中，需要调整四个电机的PWM输入而达到对飞行器的位置 (x,y,z)和姿态 (θ,φ,φ)控制。因此，在设计控制算法时，采用内外双闭环控制策略。先设计内环姿态角控制算法，再设计外环位置控制算法。其中，外环控制位置，飞行器按照目标轨迹信号进行飞行或到达期望参考位置并提供内环的期望输入；通过非线性约束条件反解，可得到内环姿态环的期望输入，通过姿态控制器控制姿态角，保证飞行器姿态稳定。控制框图如下，其中，(xcmd,ycmd,zcmd,θcmd,φcmd,φcmd)为位置和角度的期望值，(x,y,z,θ,φ,φ)为位置和角度的实际值，(Ux,Uy)为X、Y 方向的控制量输出，(U1,U2,U3,U4)为虚拟控制量，(u1,u2,u3,u4)为实际输入给无人机电机的PWM值。

图2 四旋翼飞行器系统控制框图

3.1 姿态环控制算法设计

LQR（Linear Quadratic Regulator）即线性二次型调节器，是一种基于状态空间模型的最优控制算法，其最优解具有统一的表达式，容易快速地求解出状态反馈控制率，使系统快速达到预定状态并使系统性能指标最优。针对四旋翼飞行器系统，采用输出跟踪系统的解决模式，使输出量始终跟踪输入量的变化，因此，转化为保证误差在0平衡状态[11]。

采用如下模型：

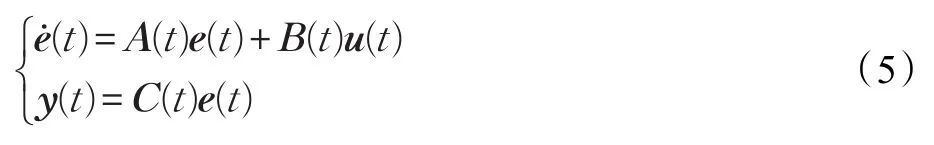
则最优控制向量为：

使以下性能指标达到最小值：

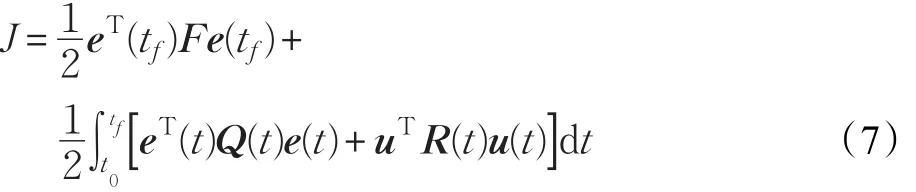
其中，输出误差向量e(t)=z(t)-y(t)，z(t)为理想输出向量，F,Q(t),R(t)为加权矩阵且为非负矩阵[5]。

根据数学模型，令 φe=φcmd-φ ，取为状态变量，则偏航角的状态空间模型为：

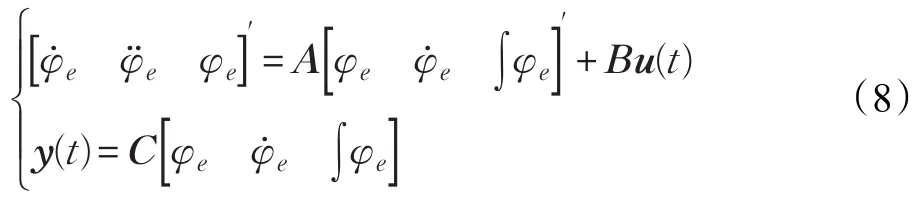
LQR算法中的Q(t)和R(t)分别是对状态变量和输入向量的加权矩阵，通常情况下，R(t)为对称的正定矩阵，Q(t)为对称的半正定矩阵，在工程应用中，经常取为对角阵。最终系统的动态性能，取决于Q(t)和R(t)的选择。利用Matlab中的 K=lqr（A，B，C，D）函数可求解出最优反馈矩阵K。同理，可写出滚转角和偏航角的误差状态空间模型，以便后续试验调整Q(t)和R(t)参数。

3.2 非线性约束条件

由飞行器建模可知，外环位置和内环姿态建模的坐标系存在一个转换关系，因此，飞行器内环的滚转角和俯仰角的期望值是由外环X方向和Y方向的控制量反解得到，存在以下非线性约束关系：

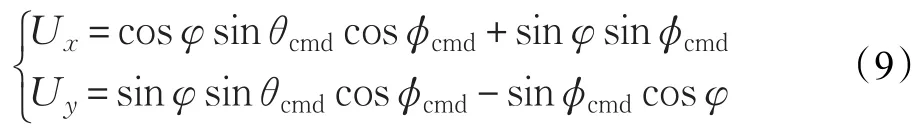
因此，通过上述关系反解推导出俯仰角和滚转角的期望值为：

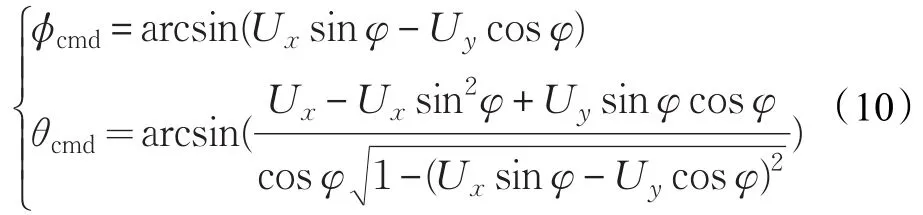
3.3 位置环控制算法设计

由于四旋翼飞行器是典型的非线性系统，非线性控制算法对模型的准确性依赖较高，因此，在模型存在不确定的因素时，PID控制算法更加实用，并且鲁棒性好[12]。

根据模型所设计的位置PID控制算法为：

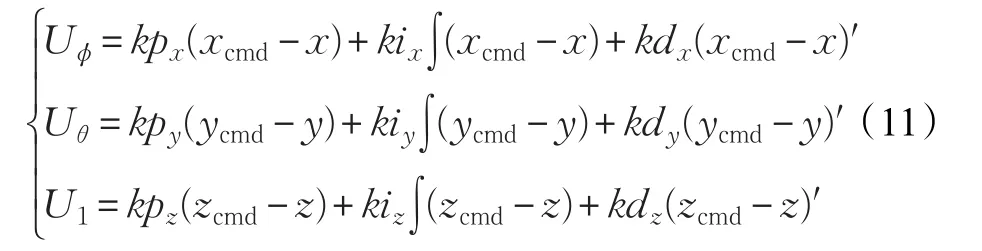
根据上述控制算法，搭建Simulink框图，进行位置外环仿真，确定PID控制算法参数的大致范围。下一章将对所设计的控制算法进行试验。

4 实验验证

将上章的内外环控制算法用于Qball-X4四旋翼无人飞行器，进行姿态控制和定点悬停控制试验，对控制算法进行验证。

4.1 姿态试验

由于三个姿态角分别由U2,U3,U4分别控制，且控制量由位置环解算得到，因此在调试姿态角参数时，可以将内环外环独立分开，然后将姿态环分通道，单独调试。以偏航角为例，图3为偏航角Simulink控制图，考虑到电池在工作时会出现电量的高低不同，因此设计两个最优反馈控制量ki_yaw_up和ki_yaw_down，保证飞行器在不同电量时，飞行状态的稳定。LQR控制框图如图3。

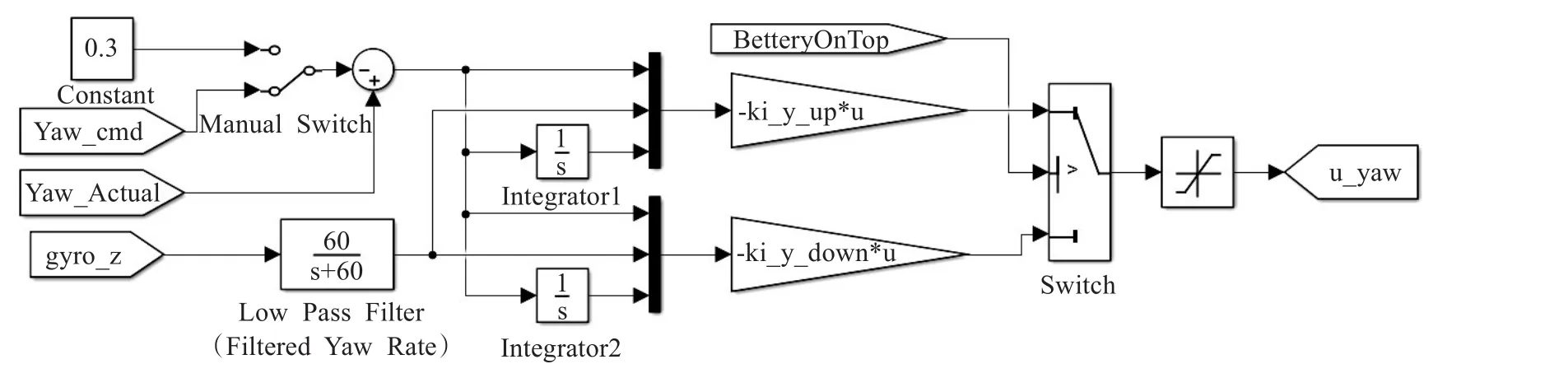
图3 偏航角LQR控制框图

在调节偏航角时，手动设置总升力U1=0.15,U2=U3=0，偏航角控制量U4由控制算法给出。通过观察偏航角变化，调整Q和R参数，使偏航角达到稳定。同理，另外两个角使用相同的调试方法。在调试时发现，Q(t)对角阵中的对应加权数值的大小，代表了控制量对输出量的控制作用，加权数值越大，表示控制作用越明显，超调量变大，响应速度变快。R(t)则显示了控制量的大小而引起的能量消耗，加权数值越大，控制量越小[13]。综合系统的动态性能，保证控制量和响应速度的前提下，选取偏航角加权矩阵Q_yup=diag（[160 90 1]）、R_yup=1 000 和 Q_ydown=diag（[185 80 1]）、R_ydown=1 000。滚转角和俯仰角选取加权矩阵Qup=diag（[230 4 7]）、Rup=100 和 Qdown=diag（[590 22 16]）、Rdown=100。仿真结果如图4。

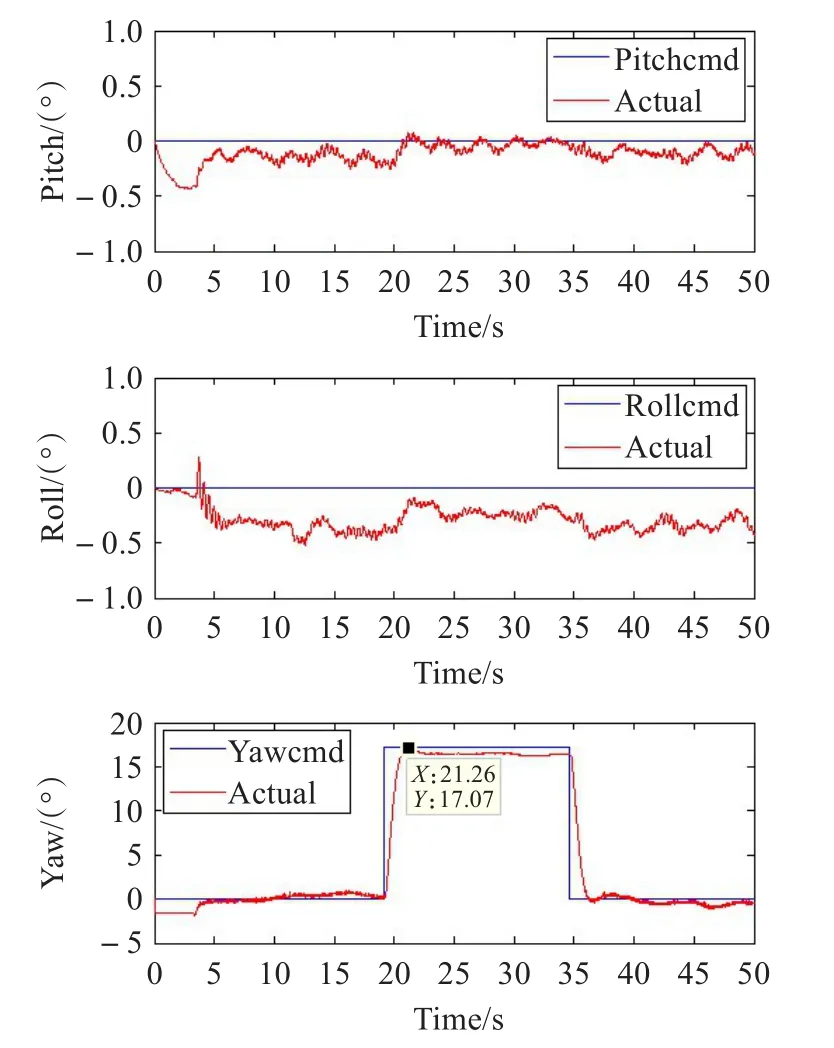
图4 姿态控制角度响应曲线

通过试验数据可得：首先设定偏航角、滚转角和俯仰角的期望值为0，观察响应曲线，俯仰角在响应初期，存在超调。达到稳定状态之后，存在一定的稳态误差（俯仰角误差为-0.2°左右，滚转角误差在-0.4°左右），在误差允许范围内。在运行一段时间后，手动将偏航角期望值改为3rad（≈17°），从试验结果看，偏航角能迅速达到预定目标，稳定后，误差在1°左右。达到稳定后，再将偏航角手动调整为0°，在控制作用下，偏航角仍能迅速调整，达到期望值0°附近，并且上下波动。试验结果表明，姿态控制器能达到预期效果。

4.2 悬停试验

通过试验调试，在Simulink的基础上，整定的位置环PID参数如下：

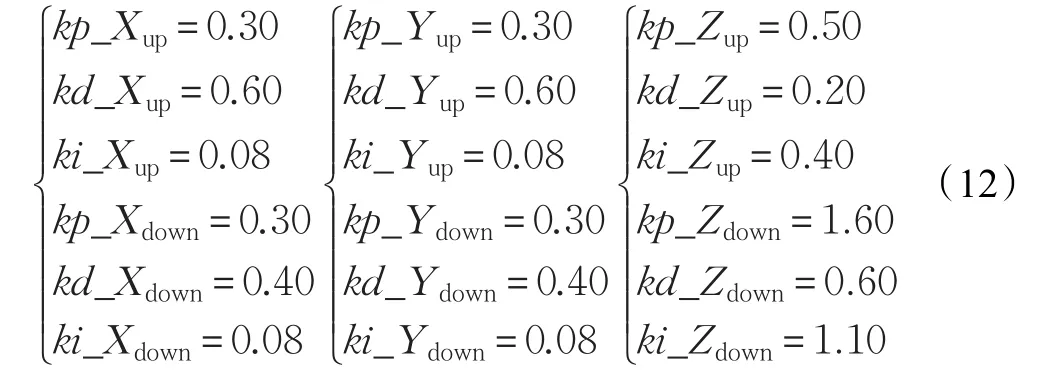
根据上述参数，设定初始位姿期望值(xcmd,ycmd,zcmd,φcmd)=(0,0,0.3,0)，进行飞行器定点悬停试验。试验的角度和位置响应曲线如图5、图6。

图5 悬停控制姿态角响应曲线

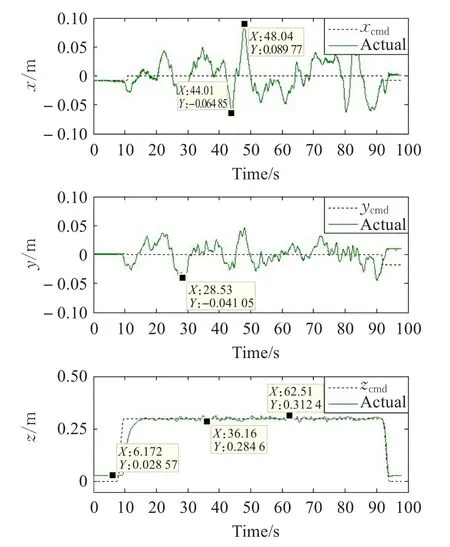
图6 悬停控制位置响应曲线

由图7得到：为保证飞行器能抵消重力起飞，需保证四个电机的PWM值输入均达到0.5左右[10]，需适当调整内环LQR控制算法的R(t)参数，以确保达到所需控制量。在飞行器起飞之后，俯仰角和滚转角在期望值附近波动，偏航角波动较大，达到稳定之后，俯仰角和滚转角的误差在±2°以内，偏航角误差在±4°以内。位置方面，X的初始位置与地面坐标系原点有0.02 m的偏差，由于在地面铺设保护措施，高度Z方面存在0.028 8 m的偏差。起飞之后，高度Z平稳达到预定0.3 m左右，误差±0.02 m，X和Z方向相应波形均在期望值上下波动，误差±0.05 m左右。在其他室内悬停试验中，位置误差均保证在±0.3 m以内，对比可知，本次位置控制在较小幅震荡范围内，在实际飞行时，上述误差均不影响控制效果，控制方法有效[14]。

图7 悬停控制实际电机PWM输入曲线

5 总结

本文依据LQR控制算法，以姿态的状态方程为内环模型，采用内环姿态环LQR控制算法，并且，为减小非线性模型的不准确，采用PID控制算法算法设计外环姿态环控制器。本套飞行器的控制算法，经过试验验证，可以达到预期的控制效果，验证了控制算法的有效性，对四旋翼飞行器实际系统有一定参考价值。在未来工作中，还会在此方法上进一步调整信号融合方面问题。

[1]刁琛.四旋翼无人飞行器非线性控制研究[D].天津：天津大学，2013.

[2]Zhao B，Xian B，Zhang Y，et al.Nonlinear robust adaptive tracking control of a quadrotor UAV via immersion and invariance methodology[J].IEEE Transactions on Industrial Electronics，2015，62（5）：2891-2902.

[3]Kerma M，Mokhtari A，Abdelaziz B，et al.Nonlinear H∞control of a Quadrotor（UAV），using high order sliding mode disturbance estimator[J].International Journal of Control，2012，85（12）：1876-1885.

[4]García R A，Rubio F R，Ortega M G.Robust PID control of the quadrotorhelicopter[J].IFAC Proceedings Volumes，2012，45（3）：229-234.

[5]张忠民，丛梦苑.基于线性二次调节器的四旋翼飞行器控制[J].应用科技，2011，38（5）：38-42.

[6]Espinoza T，Dzul A E，Lozano R，et al.Backsteppingsliding mode controllers applied to a fixed-wing UAV[J].Journal of Intelligentamp;Robotic Systems，2014，73（1）：67-79.

[7]Gao Tongyue，Tang Rui，Rao Junjin，et al.On-line adaptive controller system used on small UAV[J].Procedia Engineering，2012，45：980-985.

[8]甄子洋，浦黄忠，陈琦，等.Nonlinear intelligent flight control for quadrotor unmanned helicopter[J].南京航空航天大学学报：英文版，2015，32（1）：29-34.

[9]凌金福.四旋翼飞行器飞行控制算法的研究[D].南昌：南昌大学，2013.

[10]Lucia W，Sznaier M，Franze G.An obstacle avoidance and motion planning command governor based scheme：The Qball-X4 quadrotor case of study[C]//53rd IEEE Conference on Decision and Control，2014：6135-6140.

[11]胡寿松，自动控制原理[M].5版.北京：科学出版社，2007.

[12]何芝强.PID控制器参数整定方法及其应用研究[D].杭州：浙江大学，2005.

[13]郑大钟，王珊珊.线性二次型最优调节系统的参数稳定域[J].清华大学学报：自然科学版，1987（1）：34-37.

[14]白永强，刘昊，石宗英，等.四旋翼无人直升机鲁棒飞行控制[J].机器人，2012（5）：519-524.

[15]李瑞琪，王洪福，李瑞雪，等.基于模型参考自适应的四旋翼飞行器控制[J].计算机测量与控制，2013（12）：3260-3263.

ZHAO Yue,CHEN Yimei

School of Electrical Engineering and Automation,Tianjin Polytechnic University,Tianjin 300387,China

Design of four rotor unmanned spacecraft control algorithm.Computer Engineering and Applications,2017,53（21）：49-53.

For Qball-X4 four-rotor unmanned aircraft with its own characteristics,creating nonlinear model of system and adopting double closed-loop control algorithm with inner and outer loop are controlled by attitude and position respectively.Linear quadratic regulator is easy to solve state feedback control rate quickly,and has good robustness,thus LQR is utilized to design attitude inner loop controller.Due to the PID control algorithm has simple structure,strong robustness,thus PID is utilized to design position loop controller.Utilize Matlab/Simulink and flight test to verify control algorithm,and the result shows that the control algorithm can successfully achieve the hovering control,and achieve good control effect.

four-rotor unmanned aircraft;nonlinear model;linear quadratic regulator;PID control algorithm

A

TP273

10.3778/j.issn.1002-8331.1606-0249

天津市自然科学基金（No.15JCYBJC47800）。

赵玥（1991—），女，硕士研究生，主要研究领域为四旋翼无人飞行器，E-mail：cynthia_zyue@foxmail.com；陈奕梅（1972—），女，博士，副教授，主要研究领域为机器人控制技术。

2016-06-17

2016-08-19

1002-8331（2017）21-0049-05

CNKI网络优先出版：2016-12-21,http://www.cnki.net/kcms/detail/11.2127.TP.20161221.0843.024.html