数列综合检测(A卷)
2017-11-27江西省赣南师范大学科技学院陈国林
■江西省赣南师范大学科技学院 陈国林
数列综合检测(A卷)
■江西省赣南师范大学科技学院 陈国林
编者的话:强化对核心考点的演练、注重对经典题型的归纳,是学好数学的秘诀,基于此,本刊编辑部特开设此栏目,希望同学们能认真对待。从本期开始,如果都能撕下来保存好,对以后的复习大有裨益。
一、选择题
1.在等比数列{an}中,若有an+an+1=,则公比q的值是( )。

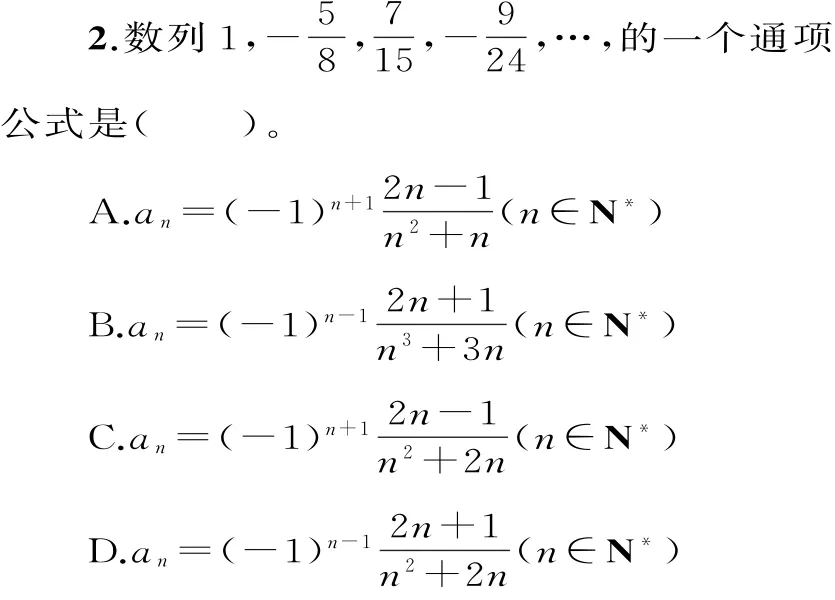
3.在等差数列an{}中,a3+a9=27-a6,Sn表示数列an{}的前n项和,则S11=( )。
A.18 B.99 C.198 D.297
4.已知等比数列an{}单调递减,若a3=,则a1=( )。
A.2 B.4 C.2 D.22
5.朱世杰是我国历史上伟大的数学家之一,他所著的《四元玉鉴》卷中“如像招数”五问有如下问题:“今有官司差夫一千八百六十四人筑堤。只云初日差六十四人,次日转多七人,每人日支米三升,共支米四百三石九斗二升,问筑堤几日”。其大意为:“官府陆续派遣1864人前往修筑堤坝,第一天派出64人,从第二天开始每天派出的人数比前一天多7人,修筑堤坝的人每天分发3升大米,共发出40392升大米,问修筑堤坝多少天”。注:1石=10斗=100升。在这个问题中,第5天应发大米( )。
A.894升 B.1170升
C.1275升 D.1467升
6.等比数列{an}中,a4=2,a5=5,则数列{lgan}的前8项和为( )。
A.1 B.2 C.4 D.8
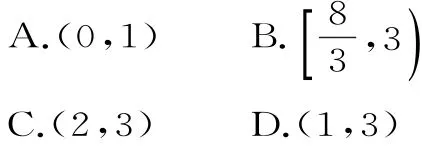
8.设Sn是等差数列an{}的前n项和,若a1=2,a5=3a3,则S9=( )。
A.-72 B.-54 C.54 D.90
9.已知等比数列{an}的前n项积记为∏n,若a3a4a8=8,则∏9=( )。
A.512 B.256 C.81 D.16
10.等比数列{an}的前项和为Sn=a·3n-1+b,则=( )。
A.-3 B.-1 C.1 D.3
11.成等差数列的三个正数的和等于6,并且这三个数分别加上3、6、13后成为等比数列 {bn}中的b3、b4、b5,则数列 {bn}的通项公式为( )。
Ab.n=2n-1Bb.n=3n-1
C.bn=2n-2D.bn=3n-2
12.下列说法不正确的一项是( )。
A.如果{an},{bn}是等比数列,那么{anbn}也是等比数列
B.如果{an}是等比数列,k是不等于0的常数,那么数列{kan}也是等比数列
C.在等差数列中,与首末两项的距离相等的两项和等于首末两项的和
D.当a1>0,q>1或a1<0,0<q<1时,等比数列{an}为递增数列
13.设等差数列an{}的前n项和为Sn,且a1>0,a3+a10>0,a6a7<0,则满足Sn>0的最大自然数n的值为( )。
A.6 B.7 C.12 D.13

A.1 B.2 C.4 D.5
15.用1或2这两个数字写成n位数,其中任意两个位置不全为1,记n位数的个数为f(n),则f(10)的值为( )。

A.144 B.135 C.123 D.111 17.在数列{an}中,对任意n∈N*,都有(k为常数),则称an{}为“等差比数列”。下面对“等差比数列”的判断:①k不可能为0;②等差数列一定是等差比数列;③等比数列一定是等差比数列;④通项公式为an=a·bn+c(a≠0,b≠0,1)的数列一定是等差比数列,其中正确的判断为( )。
A.①② B.②③ C.③④ D.①④
18.一弹性小球从100m高处自由落下,每次着地后又跳回到原来高度的处再落下,设它第n次着地时总路程为Sn,则当n≥2时,有( )。
A.Sn的最小值为100
B.Sn的最大值为400
C.Sn<500
D.Sn≤500
19.已知等比数列{an}的前n项和为Sn,则下列选项一定成立的是( )。
A.若a3>0,则a2015<0
B.若a4>0,则a2014<0
C.若a3>0,则S2015>0
D.若a4>0,则S2014>0
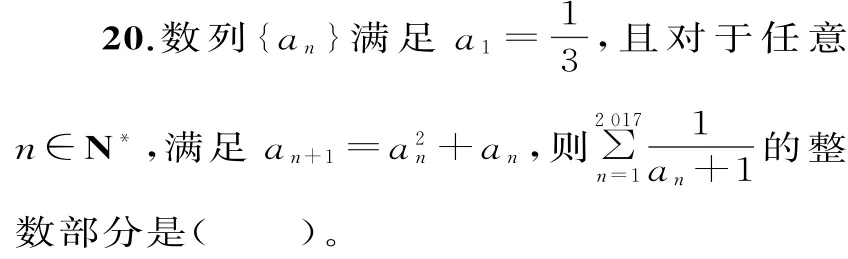
A.0 B.1 C.2 D.3
二、填空题
21.黑白两种颜色的正六边形的面砖按如图1所示的规律拼成若干个图案,则第n个图案中有白色地砖 块。
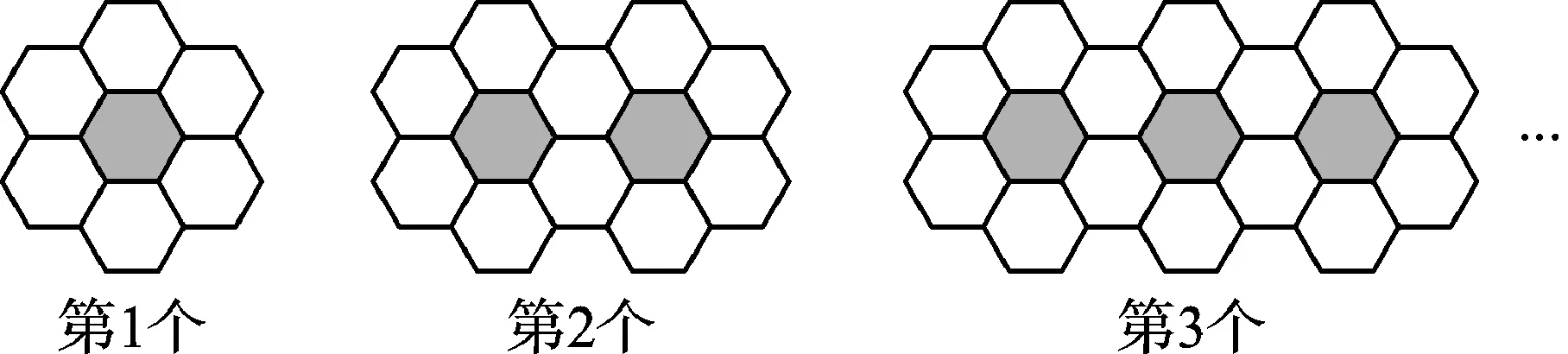
图1
22.《莱因德纸草书》是世界上最古老的数学著作之一。书中有这样一道题目:把100个面包分给5个人,使每人所得面包数成等差数列,且使较大的三个数之和的是较小的两个数之和,则最小的数为____。
23.已知等差数列{an}的前n项和为Sn,且S10=10,S20=30,则S30=。
24.已知等差数列{an}的公差为2,且a1,a2,a4成等比数列,则数列{an}的前n项和Sn=。
25.在等比数列{an}中,a6-a4=24,a3a5=64,且an>0(n∈N*),则等比数列{an}的公比q的值为____。26.已知数列an{}的首项为且满足an+1an=3an+1-2an,则数列{an}的通项公式是____。
27.图2是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,…,如此继续,若共得到1023个正方形,设初始正方形的边长为,则最小正方形的边长为____。
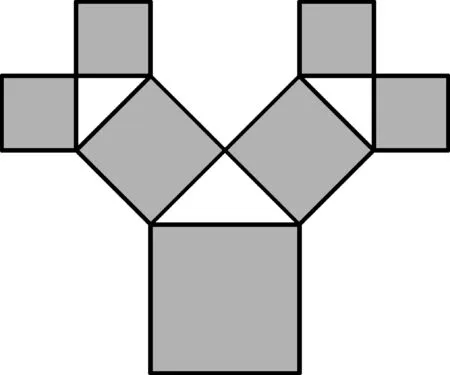
图2

35.使用计算器依照预先编制的程序进行计算,当依次输入的两个数据分别为1和1时,输出的结果为2;当依次输入的两个数据分别为m和n时,输出的结果为k;当依次输入的两个数据分别为m和n+1时,输出的结果为k+3,则当依次输入的两个数据为1和n时,输出的结果应为____。
36.设数列{an}的前n项和为Sn,若a1=2,且对任意正整数k,l,都有ak+l=ak+al,则S8的值是____。

三、解答题
41.在数1和100之间插入n个实数,使得这n+2个数构成递增的等比数列,将这n+2个数的乘积记作Tn,再令an=lgTn,n≥1,求数列{an}的通项公式。
42.等比数列{cn}满足cn+1+cn=10·4n-1(n∈N*),数列{an}的前n项和为Sn,且an=log2cn,求an,Sn的值。
43.某企业的资金每一年都比上一年分红后的资金增加一倍,并且每年年底固定给股东们分红500万元。该企业2013年年底分红后的资金为1000万元。
(1)求该企业2017年年底分红后的资金;
(2)求该企业从哪一年开始年底分红后的资金超过32500万元。
44.数列 {an}满足a1=1,an+1=3an+2n。
(1)求证数列{an+2n}是等比数列;

45.已知Sn是等差数列{an}的前n项和,且S10=55,a2,a4,a8成等比数列。
(1)求数列{an}的通项公式;

46.已知等比数列{an}的前n项和是Sn,且S18∶S9=7∶8。
(1)求证:S3,S9,S6依次成等差数列。
(2)a7与a10的等差中项是否为数列{an}中的项?如果是,它是{an}中的第几项?如果不是,请说明理由。

48.已知等差数列 an{}满足:a1=2,且a1,a2,a5成等比数列。
(1)求a2,a5的值。
(2)记Sn为数列an{}的前n项和,是否存在正整数n,使得Sn>60n+800?若存在,求n的最小值;若不存在,请说明理由。
49.已知数列an{}的前n项和为Sn,且满足a1=2,nan+1=Sn+n(n+1)。
(1)求数列an{}的通项公式an;

(2)是否存在实数a、b,使得对任意正整数p,数列an{}中满足an+b≤p的最大项恰为第3p-2项?若存在,分别求出a与b的取值范围;若不存在,请说明理由。
(责任编辑 徐利杰)
