On Eisenstein series generated from twisting of the geometric series

SHEN Li-chien

(Department of Mathematics,University of Florida,Gainesville FL 32611-8105,USA)

沈力健

(佛罗里达大学 数学系,盖恩斯维尔 佛罗里达32611-8105,美国)

On Eisenstein series generated from twisting of the geometric series

SHEN Li-chien

(Department of Mathematics,University of Florida,Gainesville FL 32611-8105,USA)

In this paper,we will be dealing with the twisting of geometric series by the Dirichlet characters.In conjunction with the basic tool of Fourier transform,it can be used to generate all the Eisenstein series with respect to a family arithmetic groups.

Dirichlet character;conductor;Eisenstein series;Gaussian sum;Kronecker symbol;Mellin transform;modular form;Poisson summation formula;Weil’s converse theorem

沈力健

(佛罗里达大学 数学系,盖恩斯维尔 佛罗里达32611-8105,美国)

The paper is organized as follows.

The relevant properties of the Dirichlet characters and the geometric series twisted by the primitive characters are given in Sections 0 and 1.Sections 2 and 3 consist of the Mellin transform of the twisted geometric series,the derivation of the associated Fourier transform and a family of functions invariant under the Fourier transform.The Eisenstein series of weight k≥3 generated by the twisted Poisson summation formula are derived in Sections 4,5,6 and 7.In Sections 8 and 9,we provide the statement of Weil’s Converse Theorem as well as the needed background materials and the proof of the modularity of the weight on Eisenstein with respect to certain arithmetic groups.In Section 10,we consider a twisted Weierstrass η function and examine its relevancy in the context of the late work of Kronecker on the theory of elliptic functions.

0 Basic properties of χ-twisted geometric series

Let N be a positive integer.Let χ be a Dirichlet character modulo N.Extend it to the set Z so that,for all integers m and n,

(1)χ(1)=1;

(2)χ(n+N)= χ(n);

(3)χ(mn)= χ(m)χ(n);

(4)χ(n)=0 if gcd(n,N)＞ 1.

Let N′be a positive integer which is divisible by N.For any character χ modulo N,we can form a character χ′modulo N′as follows:

We say that χ′is induced by the character χ.Let χ be a character modulo N.If there is a proper divisor d of N and a character modulo d which induces χ,then the character χ is said to be non-primitive,otherwise it is called primitive;and we say N is the conductor of χ if it is primitive modulo N.We note that if N is the conductor of a character,then either N=1 or N≥3.

We shall assume N≥3 unless indicated otherwise.

The Gaussian sum gk(χ)associated with the character χ is defined as

We denote g(χ)=g1(χ).We need a lemma(cf.[1,p.5]).

Lemma 0.1 Let χ be a primitive character modulo N.Then for any integer k,

We remark for gcd(k,N)=1,the above equality holds without χ being primitive;the primitiveness of χ is needed in showing that the left hand side of the identity is zero when gcd(k,N)＞1.

Let χ be a Dirichlet character.The series∑nχ(n)anis said to be the χ-twisted series of∑

nan.

Consider

The function ϕ is generated by twisting the geometric serieswith the character χ:

where|t|＜1.

We observe that,although ϕ is derived from the geometric series under the assumption:|t|＜1,it is() defined for all t∈C except possibly at the zeros of 1−tN.

Let χd(n)=denote the Kronecker’s extension of Jacobi symbol(cf.[2,p.35]).It is well-known that χdis primitive modulo|d|(cf.[3,p.347,Theorem 5]).For d=1,we define χ1(n)=1 for all n.

We have

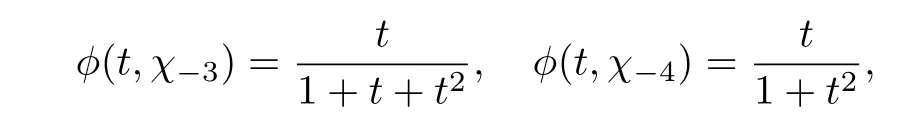
It is easy to verify the following lemma.

Lemma 0.2 Let N be the conductor of χ.

and ϕ(1,χ)=0 if χ(−1)=1.

We now derive the partial fraction expansion for ϕ(t,χ).We see that all the poles of ϕ are simple and,from(3),located at:zk=e2ikπ/N,k=1,2,...,N − 1.In fact,we have

Theorem 0.3 Suppose N is the conductor of χ.Then

where

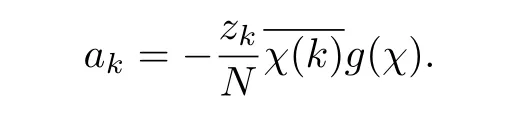
Alternatively,

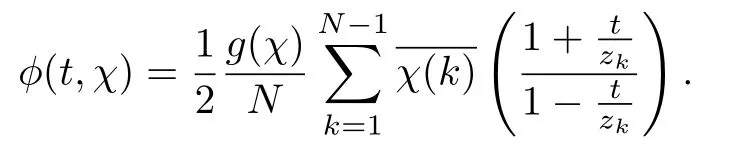
ProofFix k.We have

For the second identity,we note that

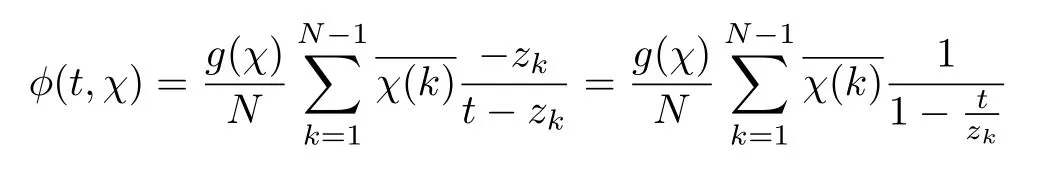
Since ak=0 if gcd(k,N)/=1,we deduce

Corollary 0.4 Suppose χ is primitive modulo N.Then the denominator of the rational function ϕ(t,χ),after canceling the common factors of its numerator and denominator,is the cyclotomic polynomial formed from the primitive roots of 1−zN=0.

From Lemma 0.2(3)and Theorem 0.3,we have

Corollary 0.5 Suppose χ is primitive modulo N.Then

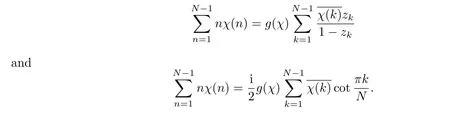
1 Partial fraction expansion of e2πxzϕ(e2πz/N,χ), χ-twisted Bernoulli polynomials and Bernoulli numbers

We will derive

Proof From Theorem 0.3,

where zk=e2iπk/N.Therefore all the poles{pk,n:k=1,2,...,N − 1,n ∈ Z}of ϕN(e2πz/N,χ)are simple and pk,n=i(k+nN).

We first compute the residue of e2πxzϕ(e2πz/N,χ)at pk,n:

We now establish the partial fraction expansion of e2πxzϕ(e2πz/N,χ).Let

We note that the infinite sum converges for all z/=pk,nand G(z)is an entire function of exponential type.We will show G(z)=0.Consider the sector S(δ)={z:z=reiθ,r ≥where δ is an arbitrary positive number less thanG(z)→ 0 as z → ∞ along the boundary of the sector S(δ).Since G is of exponential type and bounded on the boundary of S(δ),by Phragman-Lindelof theorem,G(z)is bounded in S(δ)as well its complement.Thus G is bounded on C.The claim is established by observing that G(z)tends to zero along the ray θ=

We note that

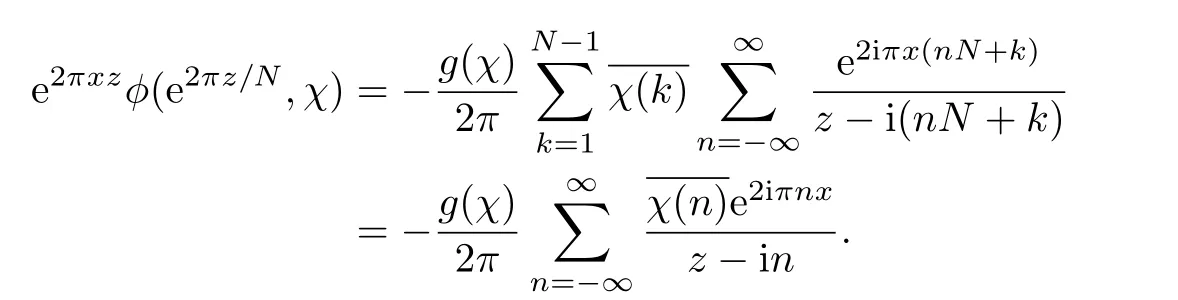
Corollary 1.2 Let N be the conductor of χ.Suppose.Then

In particular,if χ(−1)=1,

and if χ(−1)= −1,

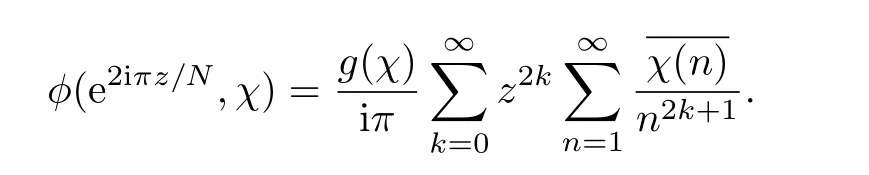
We recall the definition of the Bernoulli polynomials Bχ,k(x)associated with the Dirichlet character χ:

For x=0,it gives the Bernoulli numbers Bχ,kassociated with the character χ:

and Bχ,0=0.

From the above corollary,we deduce the trigonometric series expansion for Bχ,k(x),k≥1 and−1＜x＜1:

Setting x=0,we have,for k≥1

We add that since χ(0)=0,the term n=0 is not present in the sums.The Dirichlet L-series associated with the character χ is defined as

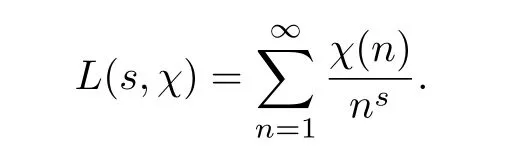
Choose χ = χd,where d is the discriminant of a quadratic field.We recall a famous theorem of Gauss:

Then,from(1.3),the values of L-series for χdare given as follows.(1)For−d＜0,

and Bχ−d,2k=0;

(2)For d＞0,

and Bχd,2k+1=0.

For N=1,the analogue of(1.1)is

where 0＜x＜1.For x=0,

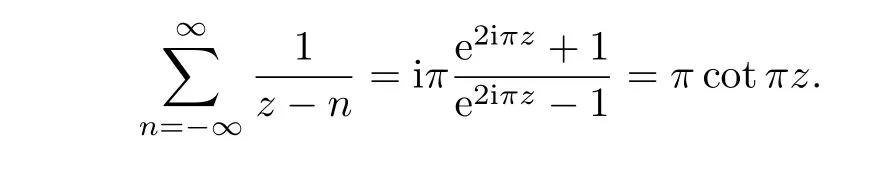
Here,the sum is interpreted as

Let z=τ∈H,where H denotes the set of the upper half plane:{τ=x+iy:y＞0}.We have

and

2 Fourier transform of ϕ(e2iπτx,χ)

Let N ≥ 3 be the conductor of χ.

The Mellin transform of ϕ(t,χ)is proved in[4,Theorem 1]:

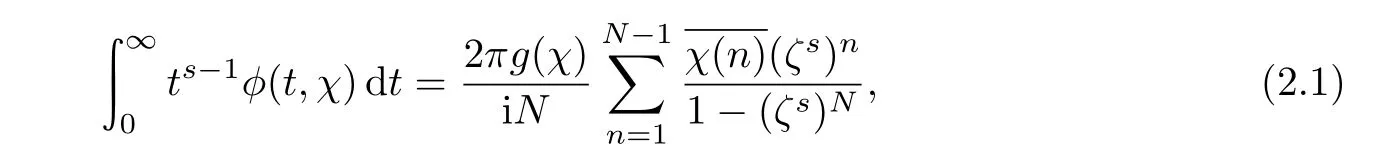
where ζs=e2iπs/N,−1 ＜ Re s ＜ 1.

The Fourier transform offis by definition

Define

We now derive

where Re α＞0.

Proof Assume α ＞0.We will remove this restriction by appealing to analytic continuation.

From(2.1),with t=e−2παxand s=iy/α,y ∈ R,

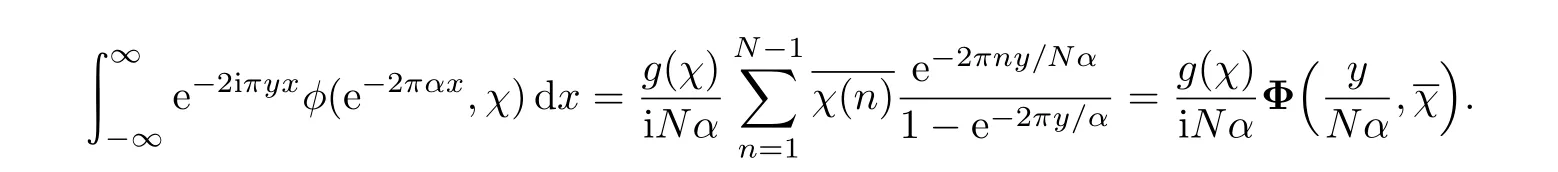
We note that,as functions of α,both sides of the above identity are analytic on the right half plane:Re α＞0.Since they coincide on the positive real axis,they are equal on the right half plane.

Using the well-known fact

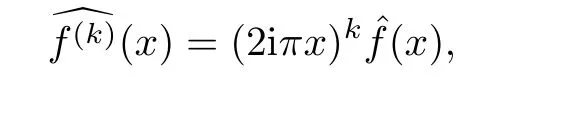
we have the following generalization(2.2).For Re α＞0,

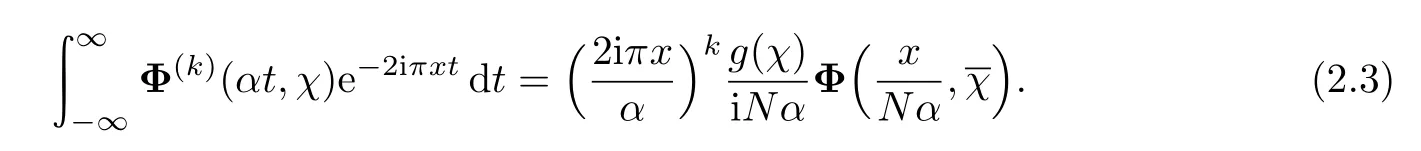
We now replace α by −iτ,τ∈ H and we obtain

Theorem 2.1 Suppose τ∈H.Then

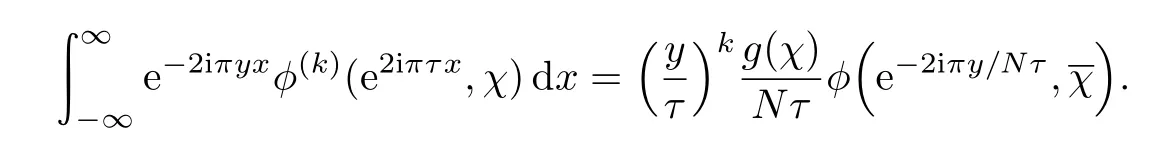
3 A family of functions invariant under Fourier transform

Define

We have

and

We now derive the Fourier transform(F(·,χ))∧(t)of F(x,χ).

Theorem 3.1 Let N ≥ 3 be the conductor of χ.Then

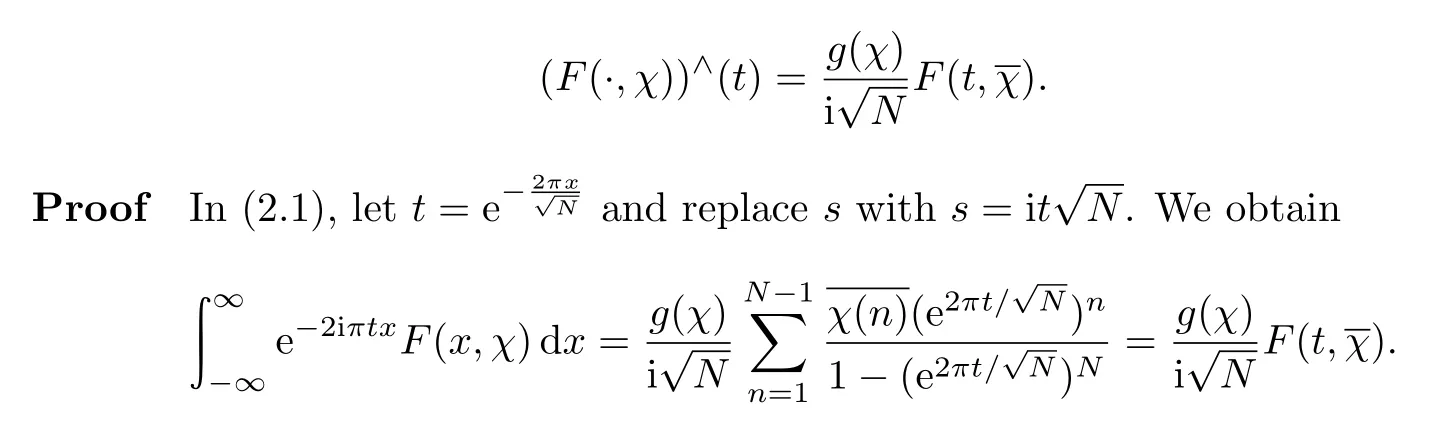
We obtain a family of functions which are invariant under the Fourier transform.Corollary 3.2 Let−d be the discriminant of an imaginary quadratic field.Then

4 Applications of Poisson summation formula

Recall the Poisson summation formula:

Lemma 4.1 Suppose τ∈ H and χ is primitive modulo N.Then

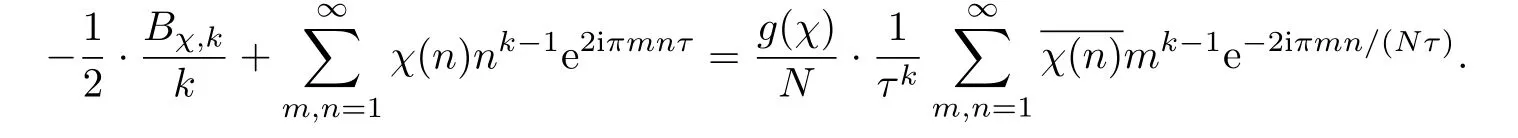
Proof Assume χ(−1)= −1.Then Φ(2k)(z,χ)is an even function of z.From Poisson summation formula,for Re α＞0,

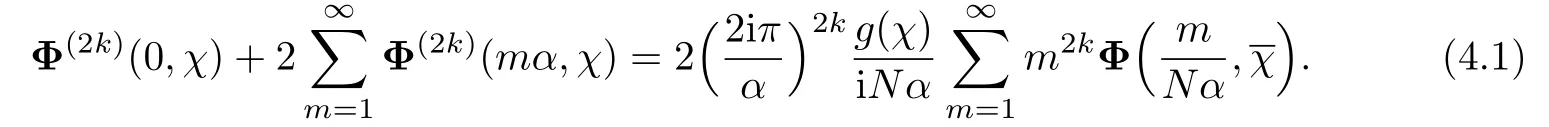
We note that when k is an odd integer,then Φ(k)(z,χ)is odd and the Poisson summation leads to a trivial identity:0=0.

Suppose Re z＞0.Then

and

From(1.2),

Thus

Replacing α by −iτ,τ∈ H,we obtain from(4.1)and(4.2)

We omit the proof for the case χ(−1)=1,since it is identical.Let ψ be primitive modulo N.For ψ(−1)= −1,define

and

For ψ(−1)=1,define

and

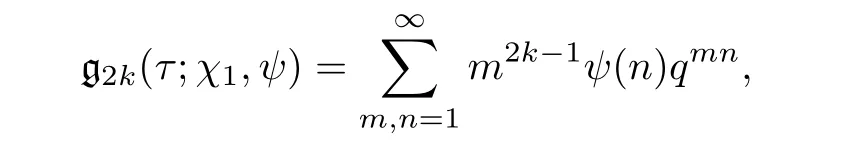
where q=e2iπτ.

We note that,for ψ(−1)=(−1)k,

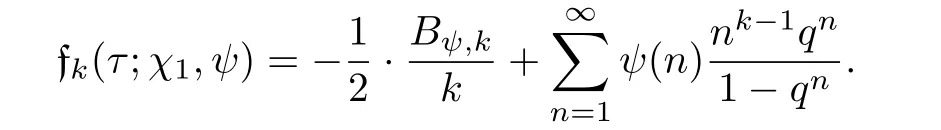
From above lemma,we have

Corollary 4.2 Suppose N ≥ 3 is the conductor of ψ and ψ(−1)=(−1)k.Then

5 Eisenstein series of weight k≥3

The following lemma plays a crucial role in the construction of the modular forms of weight k≥3.

Lemma 5.1 Let χ be a character of conductor N ≥ 3 and k ≥ 1.Then

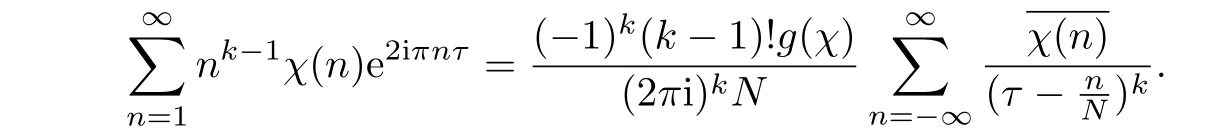
Proof Choosing x=0 in Theorem 1.1,we have

Choose z=iNτ,τ∈ H,we derive from(0.1)with t=e2iπτ,

Hence

Differentiating k−1 times gives the desired result.

We now derive the following representations of f2k+1(τ;χ1,ψ)and g2k+1(τ;χ1,ψ)as Eisenstein series.

Corollary 5.2 Suppose N ≥ 3 is the conductor of ψ and ψ(−1)= −1.Then,for k ≥ 1,

and

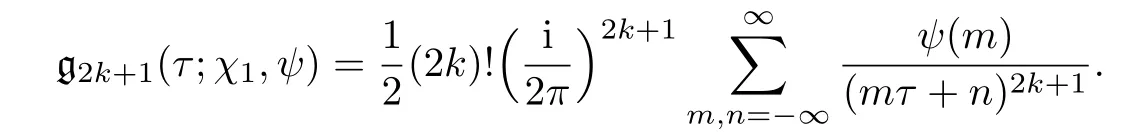
ProofWe recall that

From the lemma above,we have

We note that,since ψ(−1)= −1,

We add that since χ(0)=0,the term n=0 is not present in the sums.

The first identity clearly follows these three identities.The second identity follows readily from Corollary 4.2,

the fact

and the first identity.

We state that the identical set of results also exist for the case ψ(−1)=1 and k even.We leave the details to an interested reader.

6 Applications of the twisted Poisson summation formula

Recall the χ-twisted Poisson summation formula(cf.[1,p.8]).Let χ be a primitive character modulo N.Then

We caution the reader that in[1,p.7],due to the fact that author defines Fourier transform as

the twisted Poisson summation formula takes the form

Let ϕ and ψ be primitive characters modulo M and N and ϕψ(−1)=(−1)k.

Since the case M=1,which corresponds to ϕ = χ1,has been dealt with in the previous sections,we will assume M≥3.

Define,for k≥1,

and

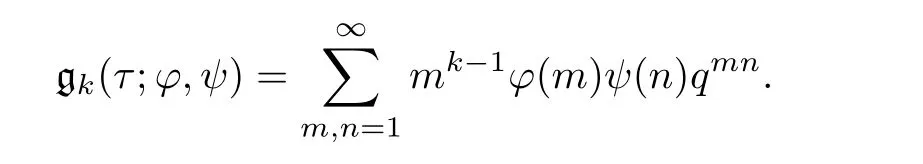
We note that f1(τ;φ,ψ)=f1(τ;ψ,φ)=g1(τ;φ,ψ);for k ＞ 1,fk(τ;φ,ψ)/=fk(τ;ψ,φ)and gk(τ;φ,ψ)=fk(τ;ψ,φ).

Corollary 6.1 Suppose φ and ψ are primitive modulo M and N and φψ(−1)=(−1)k.Then

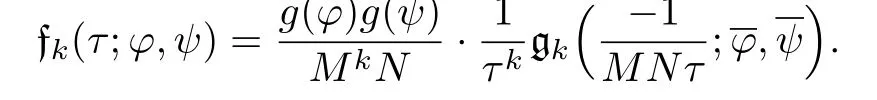
Proof The assumption that φψ(−1)=(−1)kimplies that φ(m)Φ(k−1)(mα,ψ)is an even function of m.Applying the twisted Poisson summation formula to(2.3),for Re α＞0,we obtain for k≥1,

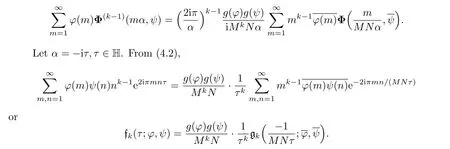
We now express fk(τ;φ,ψ)and gk(τ;φ,ψ)in terms of Eisenstein series.

Theorem 6.2 Suppose φ and ψ are primitive modulo M and N and φψ(−1)=(−1)k.Then,for k≥3,

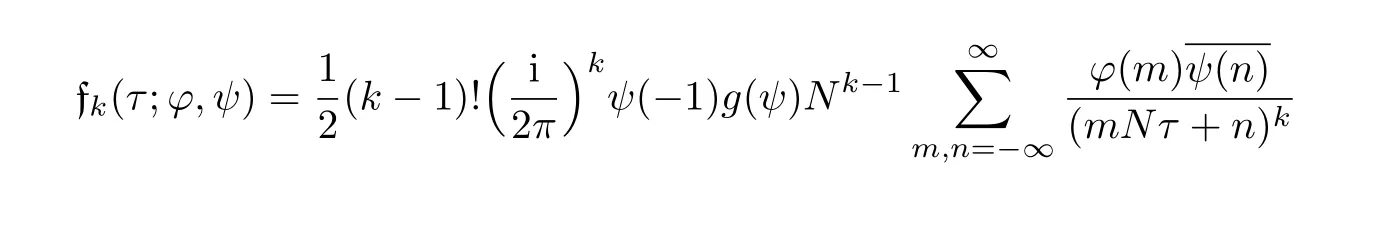
and

Proof We remark that the assumption k≥3 is to ensure that the above double sums converge absolutely.

From Lemma 5.1,

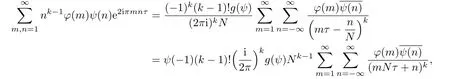
and,using the fact ϕψ(−1)=(−1)k,

This establishes the first identity.

Since

the second identity follows easily from the first one.

7 A family of Eisenstein series of weight k≥3

Let k be a non-negative integer,ψ a character modulo N and let Mk(Γ0(N),ψ)denote the space of functions f on H satisfying

(1)f is analytic on H;

(2)f is analytic at all cusps of Γ0(N);

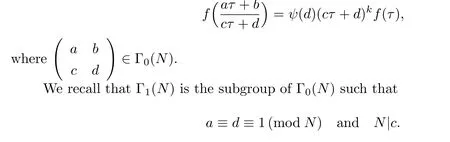
(3)Thus,iff∈ Mk(Γ0(N),ψ),then f ∈ Mk(Γ1(N)),that is,

wher

We now obtain a family of modular forms of weight k≥3 from the Eisenstein series expansions of fk(τ;ϕ,ψ)and gk(τ;ϕ,ψ)for k ≥ 3.

Theorem 7.1 Suppose ϕ and ψ are primitive characters of modulo M and N,respectively,and ϕψ(−1)=(−1)k.Then

for k≥3.

Proof We now prove the case M≥3.

The property(1)is trivial and the prove of property(2)is standard and can be found in any book in modular forms.We need to establish

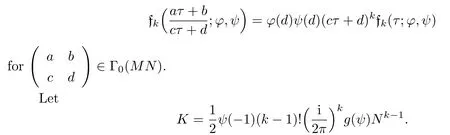
First we observe that since ψ has conductor N,

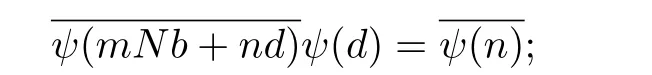
since MN|c and φ has conductor M,

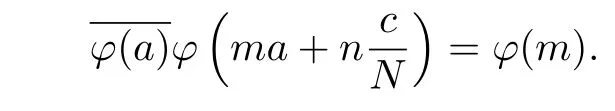
We note that since k≥3,the double sums on the right hand sides of the identities in Theorem 6.2 converge absolutely and from which we derive

The identical argument gives

for Γ0(MN).

For the case M=1,we need to establish

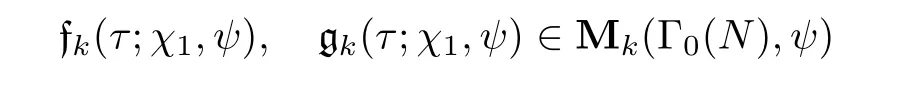
for k≥3.We again appeal to their representations as Eisenstein series,since the proof is identical to an case above,we leave it to an interested reader.

Using the same method,we can construct a family of non-holomorphic Eisenstein series:

We remark that for the case M=1,the Eisenstein series

for k=1 or 2,formally satisfies property(3).However,the double sum does not converge and cannot be used to define f1(τ;χ1,ψ)or f2(τ;χ1,ψ).In next two sections,we will circumvent the issue of convergence by appealing to Weil’s Converse Theorem to prove that Theorem 7.1 is still valid for the case k=1.The method is equally applicable to the cases k≥2,we leave the details to an interested reader.

8 Functional equations for products of two Dirichlet series

Let q=e2iπτ,τ∈ H,and let φ and ψ be characters modulo M and N,respectively,and φψ(−1)= −1.

We now consider the twist of f1(τ;φ,ψ)by a character χ modulo D.To simplify the notation,we let

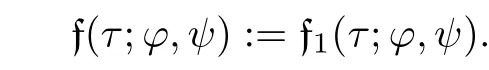
Let fχ(τ;φ,ψ)denote the twist of f(τ;φ,ψ)by χ.

Recall that,for τ∈H,

Then,from Corollaries 4.2 and 6.1 with k=1,we have

Corollary 8.1 Suppose ϕ and ψ are primitive characters modulo M and N,respectively,ϕψ(−1)= −1.Then

and

for M≥3,

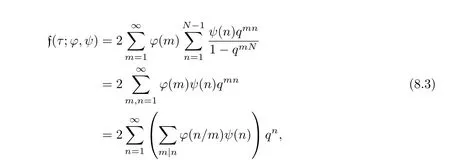
where q=e2iπτ,τ∈ H.

From(8.2)and(8.3),we have

Lemma 8.2 Suppose χ(0)=0.Then

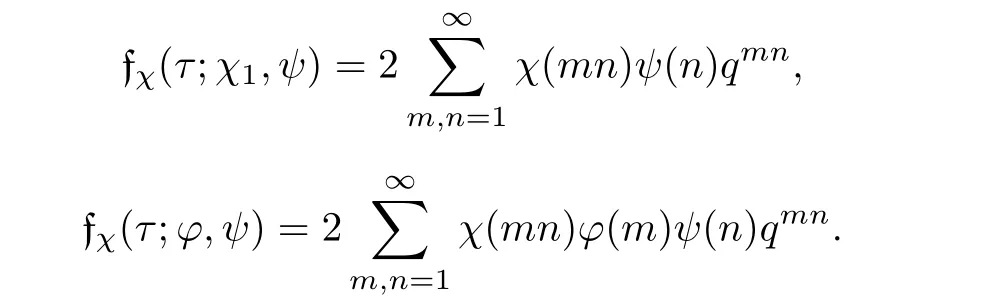
For

define the Mellin transform of fas

Then

The L-series associated with f is defined as

and we call Λ(s,f)the completed L-series of L(s,f).It is perhaps helpful to observe that

and

From above lemma,we have

Lemma 8.3

and

The main goal of this section is to establish a functional equation for Λ(fχ,s).To this end,we recall the duplication formula for the gamma function:

and the following well-known result(cf.[1,p.10]).

Suppose χ is a primitive character modulo N.Let ϵ=0 or 1 so that χ(−1)=(−1)ϵand let

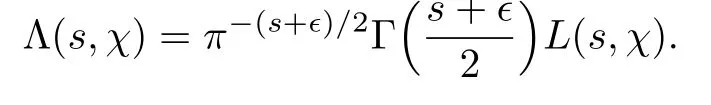
Then

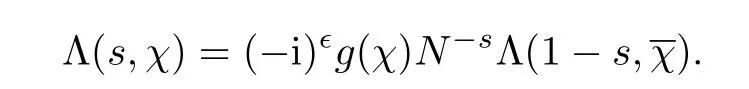
We now consider the twist of f(τ;φ,ψ)by a primitive character χ modulo D,where gcd(D,MN)=1.We first prove

Lemma 8.4 Suppose gcd(D,MN)=1,χ,φ and ψ are primitive characters modulo D,M and N,respectively and φψ(−1)= −1.Then

and

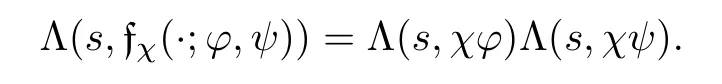
Proof We note first that since gcd(D,MN)=1,χφ and χψ are primitive modulo DM and DN,respectively.Assume χ is odd.Since φψ(−1)= −1,if ψ is odd,χφ is odd and χψ is even,

and

From the duplication formula of gamma function,

The proofs for even ψ and for even χ are identical,we omit them.

We now state the functional equation for Λ(s,fχ(·;φ,ψ)).

Lemma 8.5 Suppose gcd(D,MN)=1,χ,φ and ψ are primitive characters modulo D,M and N,respectively and φψ(−1)= −1.Then

and

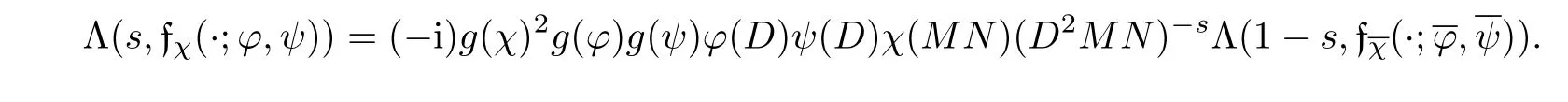
The proof follows immediately from the functional equations of Λ(s,χ)and Λ(s,χ)and the fact(cf.[1,p.111]):If gcd(D,N)=1,then

9 A family of weight one Eisenstein series

The goal of this section is to establish the following result.

Theorem 9.1 Suppose φ and ψ are primitive characters modulo M and N,respectively,and φψ(−1)= −1.Then f1(τ;φ,ψ)∈ M1(Γ0(MN),φψ).

The proof is based on Weil’s Converse Theorem for modular forms.To state the result,we shall introduce certain quantities as follows.

Let q=e2iπτ,τ∈ H and f be an analytic function defined on H.Define

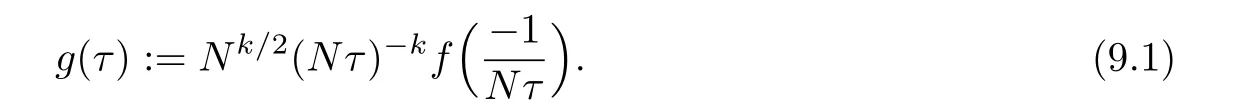
Suppose f and g have the series expansions:

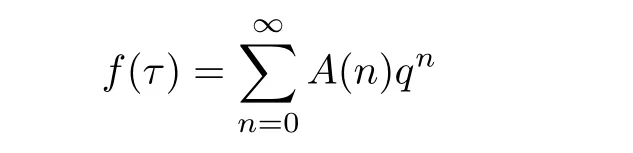
and

It is well-known(cf.[1,p.58]):Iff∈ Mk(Γ0(N),χ),then g ∈ Mk(Γ0(N),

χ)and

However,the converse is not true in general.

To obtain a version of converse result due to Weil,we introduce the following notation.Let χ be a Dirichlet character and let

The L-series and the completed L-series associated with fχand g

χare,respectively,

We state Weil’s Converse Theorem for the modular forms(cf.[1,p.61]).

Suppose

(i)ψ is a Dirichlet character modulo N,not necessary assumed to be primitive;

(ii)A(n),B(n)=O(nK)for some K＞0;

(iii) Λ(s,fχ)and Λ(s,gχ)have analytic continuation to all s∈ C except possibly with simple poles at s=0 and s=k;are bounded at infinity in every vertical strip σ1≤ Re s ≤ σ2;and satisfy the functional equation

for D=1,all gcd(D,N)=1 and χ primitive modulo D,where D is a prime.

Then f(τ)= ∑∞n=0A(n)qnis a modular form in Mk(Γ0(N),ψ).

For our purpose,only the case k=1 is needed.We now prove Theorem 9.1.

Proof Let f(τ):=f(τ,;φ,ψ):=f1(τ,;φ,ψ).

From(9.1)and Corollary 8.1,we have,

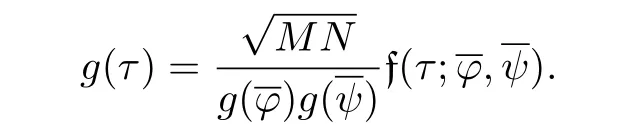
Caution!The same g carries two different meanings.

Hence

From Theorem 8.5,and the identity(cf.[1,p.81]):

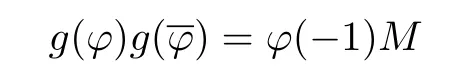
and

we obtain

Clearly Λ(s,fχ)and Λ(s,gχ)satisfy all the requirements of Weil’s theorem,the desired assertion follows.

Corollary 9.2 Suppose φ and ψ are primitive characters modulo M and N,respectively, φψ(−1)=(−1)kand χ is a primitive character modulo D. Then fkχ(τ;φ,ψ) ∈Mk(Γ0(MND2),χ2φψ).

Here fkχmeans the twist of fkby χ.

The conclusion of the corollary follows immediately from[6,p.127,Proposition 17(b)].Here we do not require gcd(D,MN)=1.

We also derive the following theorem of Hecke.

Corollary 9.3 If−d is the discriminant of an imaginary quadratic field,then f(τ;χ1,χ−d)∈ M1(Γ0(d),χ−d).

It is interesting to note that,since(cf.[2,p.171(8)])

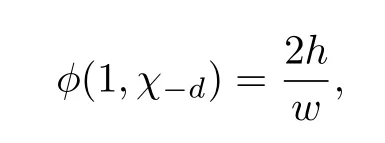
we have,from(8.2),

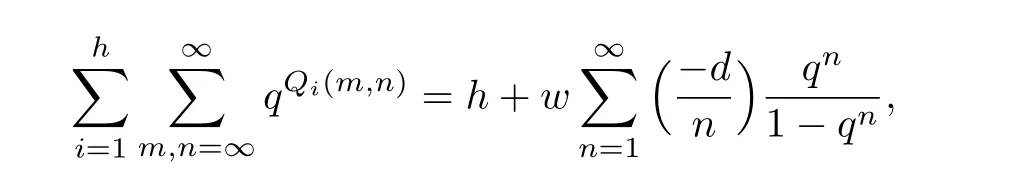
and furthermore(cf.[5,Theorem 4])where h is the class number of the quadratic fieldw the number of roots of unity in it and Qi(x,y),i=1,2,...,h,the inequivalent quadratic forms of discriminant−d.

For example,

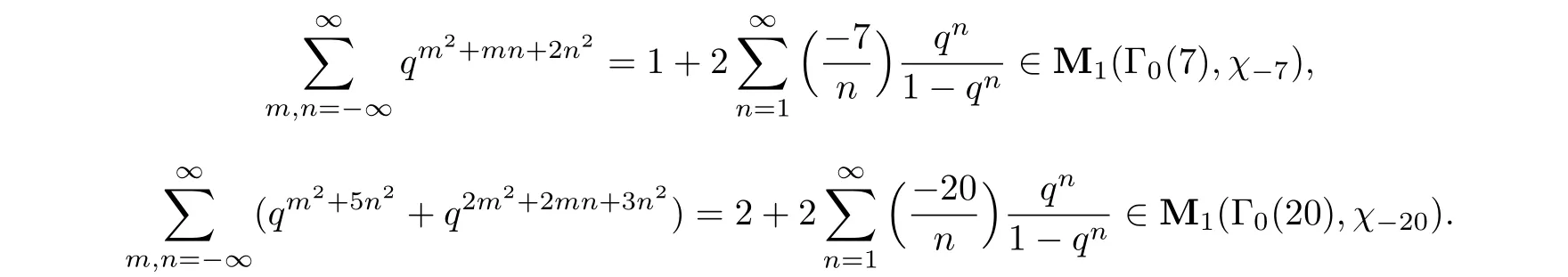
An alternative proof of Theorem 9.1 using the properties of the η function of Weierstrass can be found in[7,p.138]and a proof of a version of Weil’s theorem is given in[1,p.60].

The relevance of Theorem 7.1 is that,modulo some details,all Eisenstein series associated with the group Γ1(N)can be constructed from the linear combinations of these modular forms.We refer the details to[7,Theorem 4.8.1].

10 Kronecker’s double series and a generating function for fk(τ;φ,ψ)

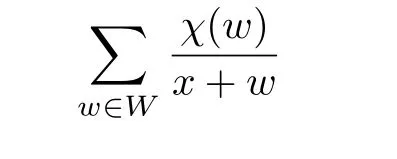
It seems relevant and appropriate to start this section quoting Andre Weil(cf.[8,p.69]).In 1890 and 1891,Kronecker began to give special emphasis to the series which he appeared to have regarded at that time as the cornerstone of the whole theory of elliptic functions.In dealing with it,Kronecker tried various methods of summation,including the method

and even a variant of Kronecker summation based on the strange series

Eventually he found Eisenstein summation to be the most appropriate procedure.This is the method we shall follow here.

Here W={mµ +nν :m,n ∈ Z}and χ(mµ +nν)=e2iπ(mµ+nν)denotes a character of the additive group W,where 0≤ µ,ν＜ 1.

We will consider the following twisted Kronecker sum:

and,for now,we ignore the issue of convergence.

Suppose χ is primitive modulo N,from Lemma 0.1,

Thus,for M,N ≥ 3,which corresponds to that case 0＜ µ,ν＜ 1,formally,we can rewrite the left hand side of(10.1)in terms Kronecker’s double series:

When M=1,which corresponds to the caseµ=0,the series clearly diverges and we avoided the difficulty by appealing to the Weil’s Converse Theorem.

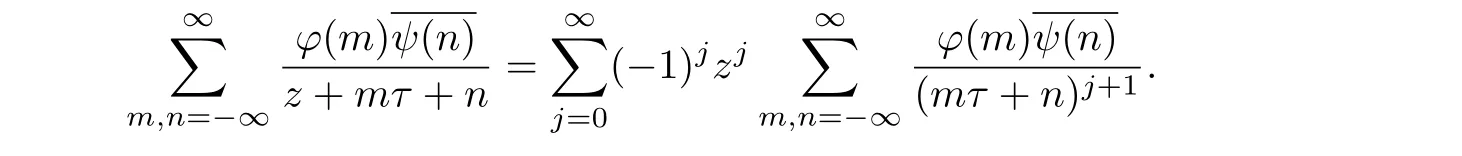
We note that since M,N≥3,the term corresponding to the index(m,n)=(0,0)is not present in the sum(10.1)and Replacing τ by Nτ,we can regard the above sum as the generating function for fk(τ;ϕ,ψ)modulo the constants.

We now introduce the method of Eisenstein summation mentioned earlier.

Replacing z by i(z+mτ)/N in(1.1),we have,

From the definition of ϕ(t,χ),

We will establish the following theorem.

Theorem 10.1 Suppose φ and ψ are primitive characters modulo M and N,respectively,φψ(−1)= −1 and M,N ≥ 3.Then

First we need to recall an identity(cf.[4,p.1101,(1.1)]):

For basic properties of the Jacobi theta functions,we refer readers to[9,Chapter XXI].ProofFrom Lemma 0.1,since φ is primitive modulo M,

Putting all above together,

The first identity follows by setting x=0 and replacing πz by z.

Set x=0 in(10.3),the second identity follows easily from(0.1).

Lemma 10.2We have

Substituting the series expansion at z=0 withand b=2iπn/N,into the identity in Theorem 10.1 and comparing the coefficients,we obtain

Corollary 10.3 If ϕψ(−1)= −1.Then

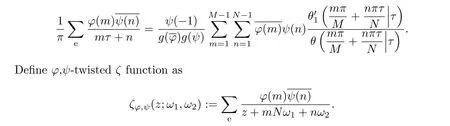
Theorem 10.4 Suppose ω,ω ∈ C andand ψ are primitive characters

12modulo,respectively,M ≥ 3 and N ≥ 3 with φψ(−1)= −1.Then ζφ,ψ(z;ω1,ω2)is an even function of z and

Then

This clearly implies the conclusion.

Acknowledgements This paper is from a part of the lecture series given by the author during his visit to the East China Normal University from June 22 to June 28,2017.The author would like to take this opportunity to thank Professor Zhi-Guo Liu and his graduate students for their hospitality and enthusiasm.A particular gratitude goes to Dr.Min-Jie Luo for his excellent assistance in converting the original manuscript to the official format of the journal.

[1]BUMP D.Automorphic Forms and Representations[M].Cambridge:Cambridge University Press,1997.

[2]COHN H.Advanced Number Theory[M].New York:Dover,1980.

[3]BOREVICH Z I,SHAFAREVICH I R.Number Theory[M].New York:Academic Press,1966.

[4]SHEN L C.On the modular equations of degree 3[J].Proceedings of AMS,1994,122(4):1101-1114.

[5]SHEN L C.On a class of q-series related to quadratic forms[J].Bulletin of the Institute of Mathematics Academia Sinica,1998,26(2):111-126.

[6] KOBLITZ N.Introduction to Elliptic Curves and Modular Forms[M].2nd ed.New York:Springer-Verlag,1993.

[7] DIAMOND F,SHURMAN J.A First Course in Modular Forms[M].Berlin:Springer,2005.

[8] WEIL A.Elliptic Functions According to Eisenstein and Kronecker[M].Berlin:Springer-Verlag,1976.

[9]WHITTAKER E T,WATSON G N.A Curse of Modern Analysis[M].4th ed.Cambridge:Cambridge University Press,1958.

(责任编辑:林 磊)

由几何级数的扭曲生成的艾森斯坦级数

本文借助狄利克雷特征处理了几何级数的扭曲.结合傅里叶变换的基本工具,生成了一族算术群的所有艾森斯坦级数.

狄利克雷特征; 导子;艾森斯坦级数;高斯和;克罗内克符号;梅林变换;模形式; 泊松求和公式; 韦伊逆定理

2017-03-29

沈力健,男,教授,研究方向为函数论.E-mail:shen@uf l.edu.

O174 Document code:A

10.3969/j.issn.1000-5641.2017.06.001

1000-5641(2017)06-0001-24