高中数学教学中学生解题能力的培养

史晓伟

(江苏省连云港市新浦中学，江苏 连云港 222002)

高中数学教学中学生解题能力的培养

史晓伟

(江苏省连云港市新浦中学，江苏 连云港 222002)

高中的数学的解法具有多样性和变通性.在教学中应该引导学生学会思考，学会发散性思维，利用已有的知识去学会从不同角度去思考和寻求解法.培养学生辩证思维和全面思考能力，学会变通和冲破定势思维的约束.

导数试题；解法；思考

高中数学的试题的解法具有复杂性，多样性和变通性等特点，在教学中要引导学生学会多角度思考，学会利用已有的知识去学会思考，培养学生的解题思维的流畅性，即在短时间内产生大量的猜想，对一个问题有多种多样的思路；引导学生学会思维的变通性，即能冲破思维定势的约束，及时调整思维方式；从学生学习的实际出发，培养学生思维的独特性，也称思维的新颖性，即大胆的新设想、新思路.

1.引导学生学会从不同角度寻找解题思路

例题1 已知函数f(x)=x2-2acoskπ·lnx(k∈N*，a∈R，且a>0)．

(1)讨论函数f(x)的单调性；

(2)若k=2010，关于x的方程f(x)=2ax有唯一解，求a值.

分析本题主要考查函数、导数、对数函数、三角函数等知识的理解和运用能力，考查函数与方程、数形结合、转化和化归、分类讨论等数学思想方法．第(1)问是要求学生准确地确定分类的标准；第(2)问，要求正确审题，将方程根的问题转化为函数图象交点个数问题.

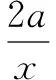
当k是奇数时，f′(x)>0，则f(x)在(0,+∞)上是增函数;

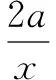
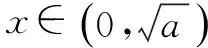
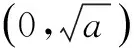
(2)若k=2010，则f(x)=x2-2alnx(k∈N*).

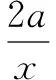
若方程f(x)=2ax有唯一解，即g(x)=0有唯一解；

令g′(x)=0,得x2-ax-a=0.因为a>0,x>0，

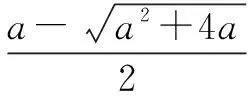
当x∈(0,x2)时，g′(x)<0，g(x)在(0,x2)是单调递减函数；

当x∈(x2,+∞)时，g′(x)>0，g(x)在(x2,+∞)上是单调递增函数．

当x=x2时,g′(x2)=0，g(x)min=g(x2). 因为g(x)=0有唯一解，所以g(x2)=0.

两式相减得alnx2+ax2-a=0， 因为a>0，所以2lnx2+x2-1=0 (*).

设函数h(x)=2lnx+x-1，因为在x>0时，h(x)是增函数，所以h(x) = 0至多有一解．

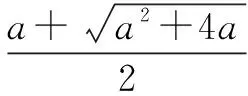
2.引导学生学会发散性思维

数学学习具有很大的复杂性，处理复杂代数式的能力及较好的心理素质和解题意志力.在解题过程中需要学生学会发散性思维，对同一个问题去多角度去思考.引导学生经过思考可用分离参数法求解该题第二问.

解法一(分离参数、数形结合)

∵y=x+lnx在区间(0,+∞)上单调增且值域为R∴y=x+lnx在(0,+∞)上有且只有一个零点，不妨设零点x=x0∈(0,1)

(1)当x+lnx=0时，方程2a(x+lnx)=x2无解

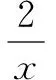
[1]王燊彬,谈高中数学教学中学生解题能力的培养[J].中学教学参考，2015(05).

[责任编辑：杨惠民]

G632

A

1008-0333(2017)30-0033-02

2017-07-01

史晓伟(1980-)，江苏连云港人，本科，中学一级教师，从事高中数学教学与研究.