三原组织织物拉伸力学性能有限元仿真

李瑛慧， 谢春萍， 刘新金,2

(1. 生态纺织教育部重点实验室(江南大学)， 江苏 无锡 214122； 2. 江苏苏丝丝绸股份有限公司， 江苏 宿迁 223700)

三原组织织物拉伸力学性能有限元仿真

李瑛慧1， 谢春萍1， 刘新金1,2

(1. 生态纺织教育部重点实验室(江南大学)， 江苏 无锡 214122； 2. 江苏苏丝丝绸股份有限公司， 江苏 宿迁 223700)

为使织物在设计前就可预估其拉伸性能，对织物拉伸过程进行了有限元模拟和试验验证。通过超景深数码显微镜对织物试样的细观照片进行尺寸测量，得到纱线的几何结构参数，借助AutoCAD绘图软件建立了三原织物单胞物理模型；基于纱线拉伸试验和织物周期边界条件理论，利用有限元分析软件ANSYS研究了三原织物的拉伸性能；并将有限元仿真结果与拉伸试验结果进行对比。结果表明：织物经向拉伸时，经向平均应力、经向平均应变、纬向平均应变和泊松比的有限元模拟结果与试验结果的差异均在5%左右；经向弹性模量的有限元模拟结果与试验结果的差异也在10%以内；证明有限元仿真的可行性。

三原组织； 拉伸力学性能； 周期边界条件； 有限元仿真； 试验验证

三原组织是织物组织中的基本组织，包括平纹、斜纹和缎纹[1]，其他织物组织都是在三原组织的基础上发展变化而来的[2]。随着社会的发展，人们对织物的服用性能提出了更高的要求，而织物的拉伸等各项性能直接影响到织物的服用性能，在改善织物质量上，拉伸力学性质意义重大。

传统的产品设计是依据设计人员的经验和相关织物的相似性进行的，存在周期长、工序复杂等问题，具有未知性和不确定性，增大了产品的设计难度[3]。通过有限元方法分析织物拉伸的过程[4-5]可获得更多的材料力学信息。目前，学者们已经对织物的拉伸性能进行了一定的研究。杜凤霞[6]综合考虑了织物的结构参数，推导出平纹、斜纹织物的拉伸-伸长数学模型。Xia等[7]提出了周期性边界条件理论，用以获得织物的力学性能。王占山等[8]对织物衬垫的拉伸性能进行了数值仿真和试验验证。本文利用ANSYS有限元软件分析计算三原织物的拉伸力学参数，用纱线的拉伸性能参数来预测织物的拉伸性能，以提高生产效率并降低成本，并可为织物其他力学性能的研究提供理论方法。

1 三原组织织物细观力学模型

1.1织物试样

三原组织是各种组织的基础，本文选用原料(普梳棉)、经纬纱线密度(14.58 tex)、经纬向织物密度(52.36 根/cm× 28.35 根/cm)相同的平纹、斜纹(织物组织为二上一下)、缎纹织物(织物组织为五枚三飞)进行物理建模，利用有限元分析经向动态拉伸性能。

1.2织物细观模型

为建立织物组织细观模型，需要纱线几何参数和织物构型数据。选用固化收缩率较小的环氧树脂对织物进行处理，防止织物截面分散。通过VHX-5000型超景深数码显微镜对织物试样的细观照片进行尺寸测量，得到织物细观模型几何参数。通过显微镜观察发现，纱线截面不是规整的圆，将截面理想为椭圆形，既保证纱线之间充分接触，又避免出现接触过盈[9]。织物细观模型几何参数如表1所示。图1示出织物经向截面几何结构示意图。

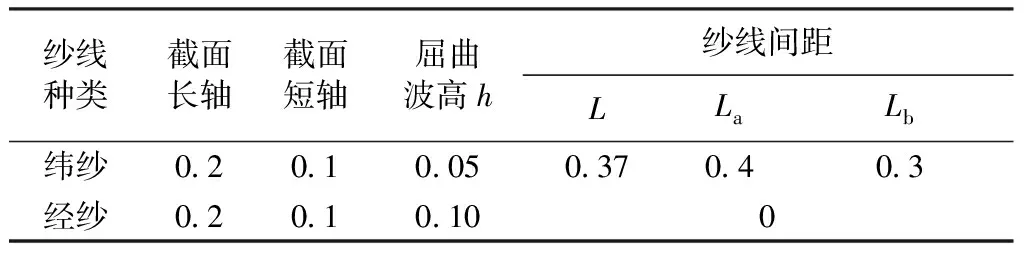
表1 织物细观模型几何参数Tab.1 Geometry parameters of meso-level fabrics mm

注：经纱间距较小，忽略为0。

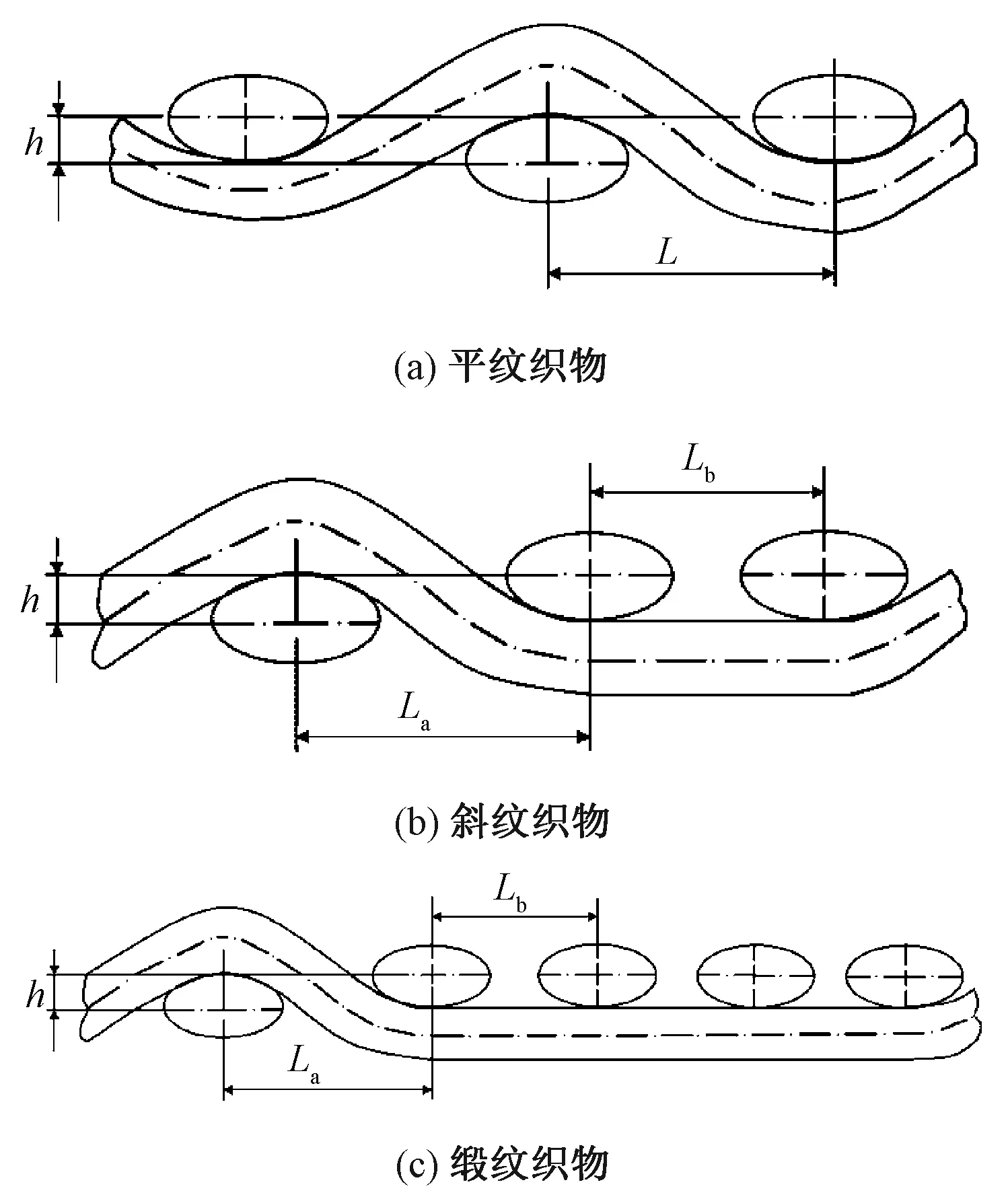
注：L—相邻经纱间距；h—屈曲波高。图1 三原组织织物经向截面几何示意图Fig.1 Geometry diagram of warp section of three-elementary weave. (a) Plain weave; (b) Twill; (c) Satin

2 三原组织织物拉伸性能有限元分析

2.1纱线拉伸试验

通过纱线拉伸试验，获得纱线拉伸性能参数[10]，并将其输入ANSYS中进行计算分析，以纱线的拉伸性能来预测织物的拉伸性能。对于平纹、斜纹、缎纹织物试样，从不同区域分别随机抽取经纱、纬纱各50根，制成长度为30 cm的纱线试样。采用YG020型等速伸长型强力仪分别对3种纱线进行拉伸试验，结果取平均值，如表2所示。

表2 纱线拉伸性能参数Tab.2 Tensile properties parameters of yarns

注：ρ表示纱线材料体积密度；E1表示纱线轴向的弹性模量；E2(E3)表示与轴向垂直的另外2个方向的弹性模量；G表示剪切模量；υ表示泊松比。

2.2三原组织织物的单胞结构

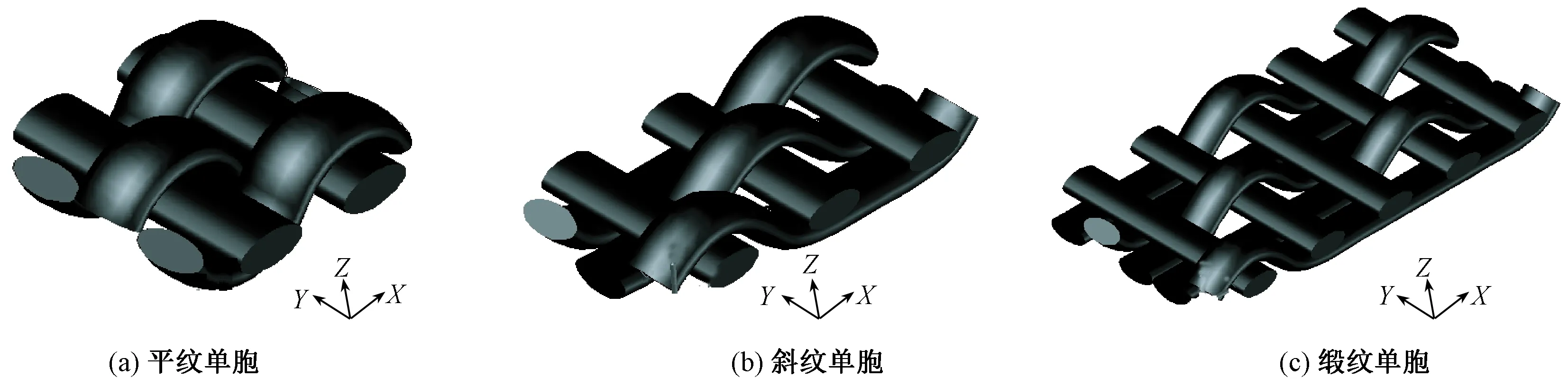
图2 三原组织织物单胞结构Fig.2 Unit-cell models of three-elementary weave. (a) Plain weave; (b) Twill; (c) Satin

织物材料在结构上具有周期性，一般只需要进行平移就能形成整个织物结构的最小重复单元，称为单胞[11]。为减少计算量与计算时间，使最小重复单元单胞构成宏观织物，依据3个试样的织物细观模型几何参数，利用AutoCAD绘图软件建立平纹、斜纹、缎纹的单胞结构。坐标原点如图2所示。图中：X轴为织物经向；Y轴为织物纬向；Z轴为垂直织物表面方向。

为使单胞的性能代表织物整体性能，单胞边界处需满足位移连续条件和应力连续条件。根据Whitcomb等[12]和Xia等[7]提出的周期性边界条件理论，推导出织物拉伸需要的周期性边界条件公式。本文仅对织物经向，即X方向进行拉伸仿真和试验。为推导织物拉伸的周期性边界条件，建立织物单胞坐标位置图，如图3所示。3种试样的单胞结构几何参数如表3所示。

注：L—沿坐标X轴方向单胞长度;W—沿坐标Y轴方向单胞长度； Z—沿坐标Z轴方向单胞长度。图3 织物单胞坐标位置图Fig.3 Coordinate position diagram of fabric unit cell

注：H为试样厚度。

法向沿X轴的面内节点约束为

(1)

法向沿Y轴的面内节点约束为

(2)

式中：UX、UY、UZ分别表示沿坐标轴X、Y、Z方向的位移；下标字母A、C表示顶点处的节点；下标等式表示对应面上的节点。

织物沿Z轴方向的结构不具有周期性，因此，法向沿Z轴的面不需要施加周期边界约束。式(1)、(2)为周期性边界条件面内节点约束，为保证有限元计算的顺利进行，还需施加棱边节点约束和顶点约束，与面内节点约束推导类似，此处不再一一列出。结合表3中的三原组织织物单胞结构几何参数，分别在有限元软件中对平纹、斜纹、缎纹织物单胞施加周期性边界条件，建立位移约束方程。

2.3单元选择和网格划分

Solid186是一个高阶三维20节点固体结构单元，具有二次位移模式，可更好地模拟AutoCAD系统建立的模型，因此，纱线单元选用Solid186。经纬纱间接触部分选用三维目标单元和接触单元TARGE170和CONTA174来定义三维接触对。织物经纬纱较为规整，选用六面体单元，采用体扫略的方式划分网格。图4示出织物单胞网格图。

2.4施加载荷并求解计算

沿坐标X方向(经向)，对单胞一端施加全约束。另一端施加Y、Z方向的约束，X方向施加100 mm/min的载荷，定义载荷步，进行有限元运算。对求解结果后处理，得到如图5～7所示的织物拉伸应力云图。

图4 织物单胞网格图Fig.4 Mesh of fabrics unit-cell. (a) Plain weave; (b) Twill; (c) Satin

图5 平纹织物拉伸应力云图Fig.5 Stress nephogram of plain weave under warp tensile. (a) Stress nephogram of warp and weft yarn; (b) Stress nephogram of weft yarn; (c)Stress nephogram of warp yarn

图6 斜纹织物拉伸应力云图Fig.6 Stress nephogram of twill under warp tensile. (a) Stress nephogram of warp and weft yarn; (b) Stress nephogram of weft yarn; (c)Stress nephogram of warp yarn

图7 缎纹织物拉伸应力云图Fig.7 Stress nephogram of stain under warp tensile. (a) Stress nephogram of warp and weft yarn; (b) Stress nephogram of weft yarn; (c)Stress nephogram of warp yarn

从织物单胞应力云图中可看出，经纬纱交织的位置应力最大，最易发生拉伸破坏。利用ANSYS/ APDL中的ETABLE命令，分别求出有限元模型中每个网格单元的平均应力、平均应变和单元体积，并将

其赋值于相应的单元表中，将单元平均应力表、平均应变表分别和单元体积表相乘，将乘积赋值于相应数据表中。对数据表求和，再求平均值。根据式(3)、(4)分别计算得到等效平均应力和等效平均应变[8]。

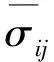
(3)

(4)

根据式(3)、(4)，对ANSYS中赋值的数据表进行计算，本文仅进行X方向(经向)的拉伸模拟，得出的有限元模拟计算结果如表4所示。

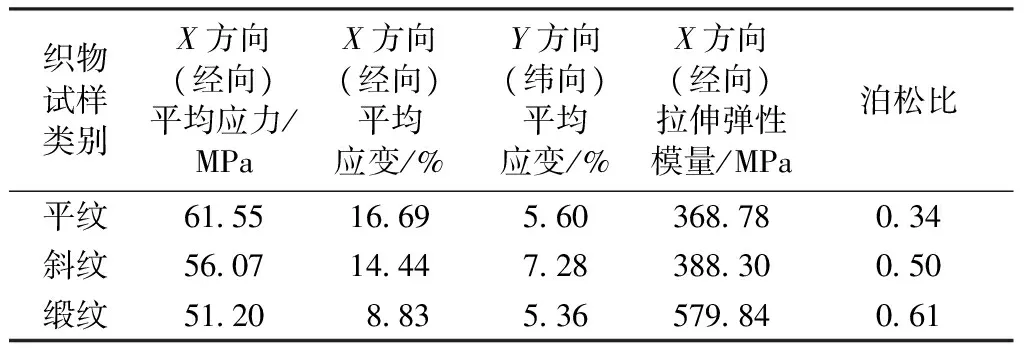
表4 有限元模拟计算结果Tab.4 Numerical simulations by FEM

3 织物拉伸试验验证

3.1试样准备

根据GB/T 3923.1—1997《织物拉伸性能 断裂强力和断裂伸长率的测定》，采用扯边纱条样法测试织物拉伸断裂性能。裁剪试样成宽度为6 cm(除去纱边最终宽度W为5 cm)，长度L为30 cm。每个试样准备5条经向样布，并随机测量试样的厚度H。如图8所示，对样布划线，其中L1、L2和L3是经向的标线(拉伸前L1=L2=L3=L0=20 mm，L0为试样原始经向标距)，可反映织物在不同部位的经向动态拉伸，W1、W2和W3是横向的标线(W1=W2=W3=W0=50 mm，W0为试样原始纬向标距)，可反映织物在不同部位的横向动态拉伸[13]。

图8 样布及标线示意图Fig.8 Sample and mark lines

3.2试验仪器

采用YG026型电子单纱织物强力试验机，测试速度为100 mm/min，预加张力为5 N，测试夹持长度为200 mm，如图8所示。每个试样经向测试5次，取平均值。

采用Olympus i-Speed3型高速摄影机，拍摄织物拉伸断裂强力试验，为方便提取特定时刻的视频照片，拍摄拉伸断裂的整个过程，记录织物纵向标线和纬向标线长度的变化。

3.3数据处理

为测得织物弹性模量和泊松比，需提取织物处于弹性变形阶段的数据。拉伸初始阶段，载荷与位移成线性关系，定义此直线部分载荷增量为△F。利用Ispeed-viewer型视频处理软件提取载荷增量为△F时刻的视频照片，导入AutoCAD软件，测量此时刻经向标线L1′、L2′、L3′，以及纬向标线W1′、W2′、W3′，计算得到经向变化量△L1、△L2、△L3，以及纬向变化量△W1、△W2、△W3，并对经向变化量求平均值△L，纬向变化量求平均值△W。将整理后的数据代入式(5)、(6)，得到弹性模量和泊松比的试验结果。

(5)

(6)

式中：E为弹性模量；μ为泊松比；σ0为弹性应力；ε0为弹性应变；△F为拉伸弹性阶段的试样拉力增量；W为试样宽度；H为试样厚度；△L为△F对应的试样长度变化量；ε1为△F对应的经向应变；ε2为△F对应的纬向应变；△W为△F对应的试样宽度变化量。

表5示出由式(5)、(6)计算得到的结果。

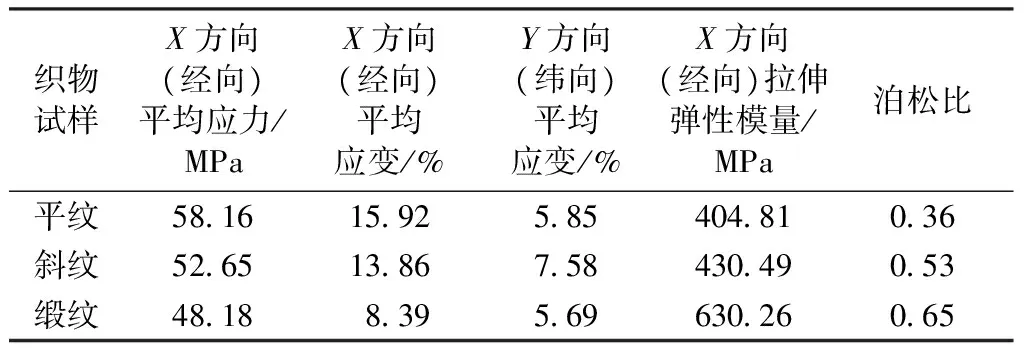
表5 试验计算结果Tab.5 Results of experiments

为测得织物经向平均应力、经向平均应变和纬向平均应变，需提取织物拉伸断裂前一瞬间的数据。利用Ispeed-viewer视频处理软件提取织物拉伸断裂前瞬间的视频照片，导入AutoCAD软件，测量此时刻经向标线L1″、L2″、L3″，以及纬向标线W1″、W2″、W3″，并对此时刻经向标线求平均值L′，纬向标线求平均值W′。将整理后的数据代入式(7)～(9)，得到织物经向平均应力、经向平均应变和纬向平均应变，如表5所示。

(7)

(8)

(9)

将有限元结果与试验计算结果对比，如表6所示。

表6 有限元模拟结果与试验结果对比Tab.6 Comparison of simulated and experimental results

表7 模拟结果与试验结果差异率Tab.7 Difference between simulated and experimental results %

注：二者差异率=(有限元模拟结果/试验计算结果-1)×100%。

由表6可看出：织物经向拉伸时，经向平均应力、经向平均应变、纬向平均应变和泊松比的有限元模拟结果与试验结果的差异均在5%左右；经向弹性模量的有限元模拟结果与试验结果的差异也在10%以内；弹性模量的结果差异较大，这主要是因为有限元模拟计算的弹性模量是由经向平均应力与平均应变的比值得到的。而试验计算的弹性模量是拉伸弹性阶段，弹性应力与弹性应变的比值得到的，因此试验得到的弹性模量比有限元计算得到结果稍大。有限元结果与试验结果虽不完全一致，但存在的误差在可接受范围，证明有限元模拟的可行性。

织物经向平均应力和经向平均应变反映织物经向的断裂强力和断裂伸长率。在纱线线密度、织物密度等条件相同时，由有限元模拟结果和试验结果可得到，平纹织物的X方向(经向)平均应力和X方向(经向)平均应变大于斜纹，斜纹大于缎纹。而平纹织物的X方向(经向)拉伸弹性模量小于斜纹，斜纹小于缎纹。这是由于织物内纱线的交织点越多，浮长线越短，拉伸时，织物中受拉系统纱线被非拉伸系统纱线挤压力越大，经纬纱间切向滑动阻力越大，有助于织物强力提高。而交织点越多，浮长线越短，纱线屈曲也就增多，拉伸时织物中屈曲纱线由弯曲而伸直所产生的织物伸长也就越大，这又会使织物的模量降低。至于Y方向(纬向)平均应变，由于平纹织物交织点多，经纬纱间滑动阻力大，所以平纹织物的Y方向(纬向)应变小于斜纹织物。而缎纹织物，由于浮长线长，织物断裂强度小，断裂时间短，缎纹织物Y方向(纬向)来不及滑动收缩就已经断裂了，使得缎纹织物Y方向(纬向)平均应变小于平纹织物。综合X、Y方向平均应变得到，平纹织物的泊松比小于斜纹，斜纹小于缎纹。

4 结 论

本文通过VHX-5000型超景深数码显微镜对织物试样的细观照片进行尺寸测量，得到了纱线的几何结构参数，借助AutoCAD绘图软件建立了三原组织织物单胞物理模型。在纱线拉伸试验和周期边界条件理论基础上，利用ANSYS模拟了三原组织织物的拉伸力学性能，并将有限元仿真结果与拉伸试验结果进行对比，得到织物经向拉伸试验时，经向平均应力、经向平均应变、纬向平均应变和泊松比的有限元模拟结果与试验结果的差异均在5%左右，经向弹性模量的有限元模拟结果与试验结果的差异也在10%以内。对织物进行经向拉伸时，平纹织物的经向平均应力、经向平均应变大于斜纹，斜纹大于缎纹，平纹织物的纬向平均应变小于斜纹，缎纹小于平纹，平纹织物的经向弹性模量、泊松比小于斜纹，斜纹小于缎纹。本文对平纹、斜纹、缎纹织物单胞的拉伸力学性能进行了仿真，验证了有限元仿真的正确性，以纱线的拉伸性能来预测织物的拉伸性能，提高生产率并降低成本。本文模拟方法可推广到织物其他力学性能的研究，为进一步分析织物力学性能提供理论基础。

FZXB

[1] 顾平. 织物结构与设计学[M]. 上海：东华大学出版社, 2006: 14-21.

GU Ping. Fabric Structure and Design[M]. Shanghai: Donghua University Press, 2006: 14-21.

[2] 姚继明. 三原组织的数字化处理初探[J]. 武汉纺织工学院学报, 1999, 12(2): 75-77.

YAO Jiming. The first probe of the digital treatment of three-elementary weave[J]. Journal of Wuhan Textile Science & Technology Institute, 1999, 12(2): 75-77.

[3] 陈国华. 机织物拉伸断裂过程模拟及强度预测[D]. 上海：东华大学, 2006: 1-22.

CHEN Guohua. The tensile breaking progress simulation and strength prediction of woven fabric[D]. Shanghai: Donghua University, 2006: 1-22.

[4] SUN B Z, WANG Y, WANG P, et al. Investigations of puncture behaviors of woven fabrics from finite elementanalyses and experimental tests[J]. Textile Research Journal, 2011, 81(10): 992-1007.

[5] NG S P, TSE P C, LAU K J. Numerical and experimental determination of in-plane elastic properties of 2/2 twill weave fabric composites[J]. Composites Part B, 1998, 29(6): 735-744.

[6] 杜凤霞. 机织物拉伸-伸长性能研究[D]. 青岛：青岛大学, 2003: 1-21.

DU Fengxia. A study on tensile stretching performance of woven fabric[D]. Qingdao: Qingdao University, 2003: 1-21.

[7] XIA Z H, ZHOU C W, YONG Q L, et al. On selection of repeated unit cell model and application of unified periodic boundary conditions in micromechanical analysis of composites[J]. International Journal of Solids and Structures, 2006, 43(2): 266-278.

[8] 王占山, 吕利叶, 张佳丽, 等. 聚四氟乙烯/芳纶破斜纹织物衬垫拉伸性能数值仿真[J]. 纺织学报, 2016, 37(7): 71-76.

WANG Zhanshan, LÜ Liye, ZHANG Jiali, et al. Numerical simulation of tensile properties of polytetrafluoroethylene /Kevlar broken twill fabric liner[J]. Journal of Textile Research, 2016, 37(7): 71-76.

[9] 张天阳. 机织物防刺性能的有限元分析[D]. 上海：东华大学, 2011: 1-29.

ZHANG Tianyang. Stab resistance behaviors of woven fabrics by finite element analysis[D]. Shanghai: Donghua University, 2011: 1-29.

[10] 马倩. 机织物撕裂破坏机理的有限元分析[D]. 上海：东华大学, 2010: 8-14.

MA Qian. Finite element analyses of woven fabrics tearing damage[D]. Shanghai: Donghua University, 2010: 8-14.

[11] 薛亚红, 陈继刚, 闫世程. 二维机织复合材料力学分析中的周期性边界条件研究[J]. 纺织学报, 2016, 37(9): 70-76.

XUE Yahong, CHEN Jigang, YAN Shicheng. Periodic boundary conditions for mechanical property analysis of 2-D woven fabric composite[J]. Journal of Textile Research, 2016, 37(9): 70-76.

[12] WHITCOMB J D, CHAPMAN C D, TANG X D. Derivation of boundary conditions for micromechanics analysis of plain and satin weave composites[J]. Journal of Composite Materials, 2000, 34(9): 724-747.

[13] 刘晓艳. 基于有限元流场分析的集聚纺成纱质量及织物性能研究[D]. 无锡：江南大学, 2015: 27-39.

LIU Xiaoyan. Research on yarn and fabric property of condensing spinning by flow numerical simulation using FEM[D]. Wuxi: Jiangnan University, 2015: 27-39.

Finiteelementsimulationontensilemechanicalpropertiesofthree-elementaryweavefabric

LI Yinghui1， XIE Chunping1， LIU Xinjin1,2

(1.KeyLaboratoryofEco-Textiles(JiangnanUniversity),MinistryofEducation,Wuxi，Jiangsu214122,China; 2.JiangsuSpcc-SilkCo. ,Ltd. ,Suqian,Jiangsu223700,China)

In order to predict the tensile properties of fabrics, numerical simulations of fabric tensile process were studied by using finite element method, and corresponding experiment verification was presented. The geometry parameters of the fabrics were obtained by observing the morphology of the fabrics by means of super depth of field digital microscope VHX-5000. The mechanical unit-cell models of the three-elementary weave were built by AutoCAD. Then, based on the experiment of yarn tensile and the periodic boundary conditions, the tensile properties of the three-elementary weave were studied using ANSYS software. Results of numerical simulations and experiments were compared. The results indicate that when fabrics are stretched along the warp direction, the error of warp average stress, warp average strain, weft average strain and poisson ratio between the simulated and the experimental results are all about 5%. Moreover, the error of warp elasticity modulus between the simulated and the experimental results is about 10%, verifying that numerical simulation using the finite element method is effective.

three-elementary weave; tensile mechanical property; periodic boundary condition; finite element simulation; experiment verification

10.13475/j.fzxb.20161205107

TB 332

A

2016-12-27

2017-02-21

中国博士后科学基金项目(2015M581722)；江苏省产学研项目(BY2015019-10，BY2016022-27)；江苏省科技成果转化项目(BA2014080)；新疆自治区重点研发项目(2016B02025-1)

李瑛慧(1993—)，女，硕士生。主要研究方向为织物力学性能。谢春萍，通信作者，E-mail：wxxchp@vip.163.com。