环Fq+vFq+v2Fq+v3Fq上的交错循环码

2017-11-22何明英

山东理工大学学报（自然科学版） 2017年1期

关键词：山东理工大学自同构码长

何明英

( 山东理工大学理学院，山东淄博 255049)

环Fq+vFq+v2Fq+v3Fq上的交错循环码

何明英

( 山东理工大学理学院，山东淄博 255049)

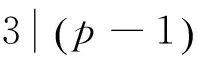
线性码；Gray映射；交错循环码；生成多项式

1 预备知识

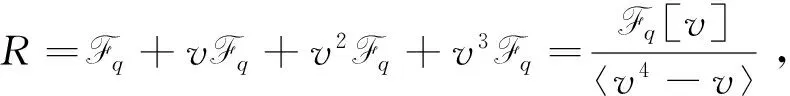
ⅰ)εi是R中的非零幂等元, 若i≠k,有εiεk=0,i=1,2,3,4.

ⅱ)在环R中有ε1+ε2+ε3+ε4=1.

ⅲ)R=Rε1⊕Rε2⊕Rε3⊕Rε4=Fqε1⊕Fqε2⊕Fqε3⊕Fqε4.

根据(ⅲ)可知对任意的r∈R, 存在s,t,u,w∈Fq使得r=sε1+tε2+uε3+wε4.

定义一个从R到Fq4的Gray映射φ为

φ(r)=(s+t+u+w,s+t-u-w,s-t+

u-w,s-t-u+w)

其中r=sε1+tε2+uε3+wε4∈R.

定义1 令r=sε1+tε2+uε3+wε4,r∈R.则r的Lee重量定义如下wL(r)=wH(s+t+u+w,s+t-u-w,s-t+u-w,s-t-u+w), 其中wH(v)表示在Fq上的向量v的Hamming重量.

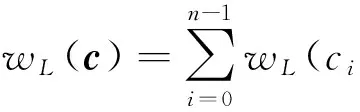
对任意c1,c2∈Rn, c1与c2的Lee距离定义为dL(c1,c2)=wL(c1-c2).

环R上码长为n的码C为Rn的非空子集,C是线性码当且仅当C是Rn的R-子模. C的最小Lee距离等于任意两个不同码字之间Lee距离的最小值. C中所有非零码字的Lee重量的最小值等于任意两个不同码字之间Lee重量的最小值.若C是线性码, 则最小Lee距离等于最小Lee重量. 在本文中，假定C是环R上的线性码.

其中ci=siε1+tiε2+uiε3+wiε4,i=0,1,…,n-1.

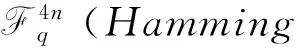
证明取z1,z2∈Fq,根据Gray映射φ的定义,对任意的c1,c2∈Rn,有φ(z1c1+z2c2)=z1φ(c1)+z2φ(c2), 可知φ是Fq-线性的.

取cj=(cj0,cj1,…cj,n-1)∈Rn,j=1,2, 其中c1,i=s1,iε1+t1,iε2+u1,iε3+w1,iε4,c2,i=s2,iε1+t2,iε2+u2,iε3+w2,iε4,i=0,1…,n-1.

则c1-c2=(c10-c20,c11-c21,…c1,n-1c2,n-1),φ(c1-c2)=φ(c1)-φ(c2).

因此dL(c1,c2)=wL(c1-c2)=wH(φ(c1-c2))=wH(φ(c1)-φ(c2))=dH(φ(c1),φ(c2)).

引理2 令C为环R上的(n,A,d)线性码, 其中n,A,d分别为码长, 码字个数和C的最小Lee距离. 那么φ(C)是域Fq上[4n,logqA,d]线性码.

证明由引理1可知φ(C)是Fq-线性的. 即φ(C)是Fq-线性码. 由Gray映射φ的定义,φ(C)的码长为4n, 从Rn(Lee距离)到Fq4n(Hamming距离)的映射φ是双射. 则可知φ(C)的维数为logqA. 由于φ为保距映射,φ(C)的最小Hamming距离为d.

令c=(c0,c1,…cn-1),d=(d0,d1,…dn-1)为Rn的两个不同元素, 则c与d内积定义如下所示

码C的对偶码定义为

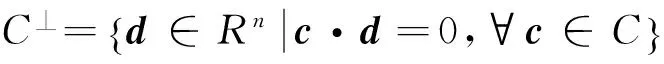
若C⊆C⊥, 则称C为自正交码. 若C=C⊥, 则称C为自对偶码.

与定理1[2]类似, 有以下结论.

定理1 令C是环R上的线性码, 则φ(C)⊥=φ(C⊥). 特别地, 当C为自对偶码时,φ(C)是域Fq上的自对偶码.

证明取c1=(c10,c11,…c1,n-1)∈Rn,c2=(c20,c21,…c2,n-1)∈Rn,

其中cj,i=sj,iε1+tj,iε2+uj,iε3+wj,iε4,sj,i,tj,i,uj,i,wj,i∈Fq,j=1,2,i=0,1…,n-1.

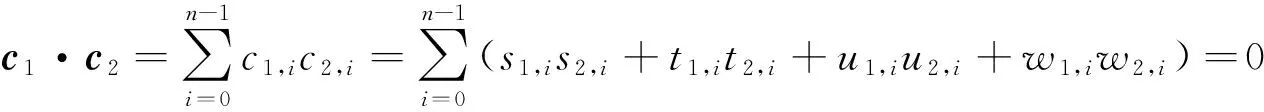
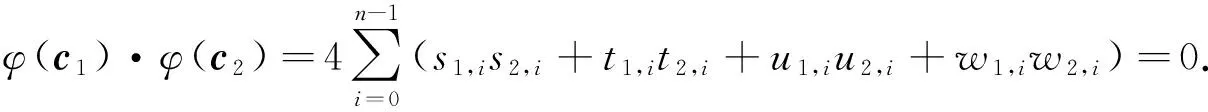
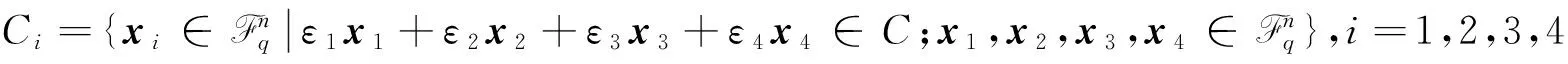
令G为环R上码C的生成矩阵, 由上式知码C是Rn的Fq-子模. 则C的生成矩阵可表示为

其中Gi分别为Ci是在环R上的生成矩阵,i=1,2,3,4.

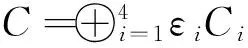
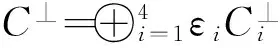
2 主要结果及其证明

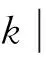
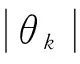
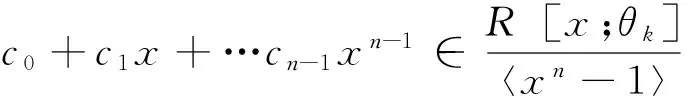
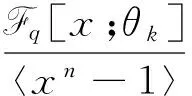
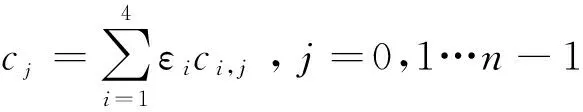
σ(c)=(θk(cn-1),θk(c0),…,θk(cn-2))∈C,

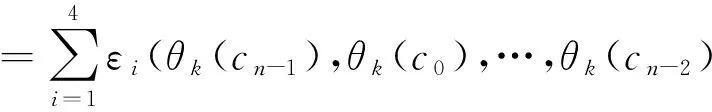
因此, (θk(cn-1),θk(c0),…,θk(cn-2))∈C, 可推出Ci是Fq上符合自同构θk的交错循环码, 其中i=1,2,3,4.

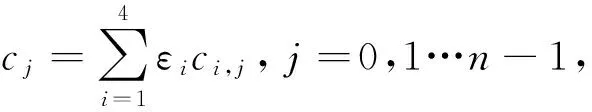
其中

故C为环R上符合自同构θk的交错循环码.

推论1 若C为环R上符合自同构θk的交错循环码, 则其对偶码C⊥也是环R上符合自同构θk的交错循环码.

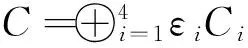
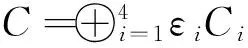
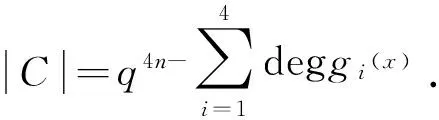
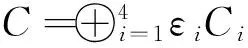
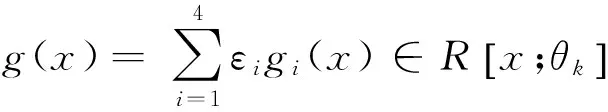
因此

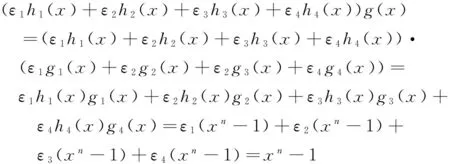
由定理4可直接得出以下推论.

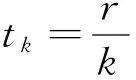
由引理6和7可直接得出以下推论.

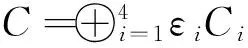
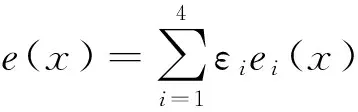
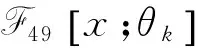
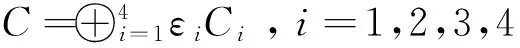
则在环R上的交错循环码C的幂等生成元为

[1]GAO J, SHEN L, FU FW. A Chinese remainder theorem approach to skew generalized quasi-cyclic codes over finite fields[J].Cryptography and Communications. 2015, DOI 10.1007/s12095-015-0140.

[2]GAO J. Some results on linear codes overFp+uFp+u2Fp[J]. Journal of Applied Mathematics and Informatics, 2015, 47(1): 473-485.

[3]GURSOY F, SIAP I, YILDIZ B. Construction of skew cyclic codes overFp+vFp[J]. Advances in Mathematics of Communications, 2014, 8(3): 313-322.

[4] GAO J. Skew cyclic codes overFp+vFp[J]. Journal of Applied Mathematics and Informatics, 2013, 31(3-4): 337-342.

[5] ZHU S, WANG L. A class of constacyclic codes overFp+vFpand its gray image[J]. Discrete Mathematics.2011, 311(23-24): 2 677-2 682.

[6]BOUCHER D, GEISELMANN W, ULMER F. Skew-cyclic codes[J]. Applicable Algebra in Engineering Communication and Computing, 2007, 18(4): 379-389.

[7]BOUCHER D, ULMER F. Coding with skew polynomial rings[J].Journal Symbolic Computation, 2009, 44(12): 1 644-1 656.

(编辑:刘宝江)

Skew cyclic codes overFq+vFq+v2Fq+v3Fq

HE Ming-ying

(School of Science, Shandong University of Technology, Zibo 255049, China)