一种基于链路预测的图聚类算法

金 超，张龙波，王 雷，安建瑞，怀 浩，王晓丹

(山东理工大学 计算机科学与技术学院，山东 淄博 255049)



一种基于链路预测的图聚类算法

金 超，张龙波，王 雷，安建瑞，怀 浩，王晓丹

(山东理工大学 计算机科学与技术学院，山东 淄博 255049)

通过重新定义传统GN算法的边介数计算，提出了一种基于链路预测方法的图聚类算法；并且在分析GNRA仍旧存在的不足的基础上，给出了其改进算法IGNRA. 通过对常用的四组数据集进行实验比较发现：所提出的GNRA算法在效率上比传统的GN算法能够明显提高，而IGNRA相比较GNRA、GN具有最低的计算复杂度.

图聚类；GN算法；链路预测；

聚类是将物理或抽象对象集合划分为簇的过程.每一个簇内尽可能相似，簇间尽可能相异.图聚类是聚类分析中一个重要的研究方向，它是将图中连接紧密的结点与边划分为一个子图，子图内结点相似性较高，子图间结点相似性较低.在社会关系网络分析[1-2]中，图聚类可以发现其中的“小世界”，即：发现社会网络中潜藏的社会结构.

1 相关研究

近年来，随着社会关系网络分析的广泛应用，图作为一种数据结构在社会关系网络分析中所起到的作用越来越大.使用图聚类[3-5]的方法对社会关系网络挖掘是目前的一个研究热点.例如，文献[6]中介绍了一种基于凝聚的层次聚类算法，即：FN(Fast Newman algorithm)算法.该算法定义了一个优化函数，每次合并时通过使优化函数值增大最多或者减少最少.该算法能够得到较好聚类结果，时间复杂度较高.文献[7]提出了一种基于结构相似性的图聚类算法，SCAN(Structural Clustering Algorithm for Networks，SCAN) 算法.该算法首先通过参数阈值获得核心结点，然后通过核心结点进行簇扩充.算法时间复杂度较低，参数好坏对聚类质量影响较大.

GN(Girvan-Newman)算法[8]是一种经典的基于分裂的层次聚类算法.在一个拥有m条边，n个结点的简单图中，通过不断的移除边介数最大的边来获得社区的划分,其中边介数是指图中通过该边的最短路径的数目.GN算法能够得到较为准确的划分结果，但是其边介数的计算，时间复杂度较高，为O(mn).当前GN算法的改进主要有两种策略，即：1.使用其他相似性度量函数取代边介数计算的策略； 2.将GN算法并行化的策略.第一种策略主要用到的方法有蒙特卡洛方法[9]，结点中心度[10]等.该方法主要是以牺牲算法的聚类精度以提升算法的运行效率.第二种策略则主要有两种方式，一个是从多源点出发计算边介数[11]，然后求和；另一个是使用Mapreduce来进行并行化计算边介数[12].使用这种策略，聚类精度较好，但编程过于复杂，对硬件要求较高.本文使用第一种策略，通过对链路预测方法的分析，利用链路预测中局部相似性指标RA(Resource Allocation, RA)[13]来取代GN算法中复杂的边介数计算，提出一种基于链路预测的图聚类算法GNRA(Girvan-Newman algorithm based on Resource Allocation, GNRA)及其改进算法IGNRA(improved Girvan-Newman algorithm based on Resource Allocation, IGNRA)算法.

2 GNRA算法

链路预测[14-16]是指通过已知的网络结构等信息预测网络中尚未产生连边的两个结点之间产生连边的可能性.链路预测可以发现网络中的缺失边.在一个网络中，假设拥有连边的两个结点边缺失，预测这两个结点之间生成连边的可能性.可以用这个可能性度量任意两个结点间的相似性.文献[13]从网络资源分配的角度提出一种指标Resource Allocation，简称RA.RA的计算主要考虑两个结点之间的共同邻居结点，因此计算时间复杂度较低.采用RA相似性代替GN算法中复杂的边介数计算，能够使算法时间复杂度得到有效降低.

2.1 相关定义

本文提出的GNRA是一种基于分裂的层次聚类算法，使用该算法不需要输入参数即可发现网络中的簇结构.该算法主要针对无向、非加权图的简单图G=(V,E)，V表示一系列的结点，E表示边.图中边数用m表示，结点数用n表示.

定义1 邻居结点

令u∈V，u的邻居结点用Nu来表示，则

(1)

定义2 RA相似性

(2)

其中u,v∈V，Nu表示结点u的邻居结点，k(z)表示结点z的度.

定义3 边结构

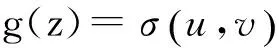
定义4 模块度

(3)

其中，m是图中的边数，Auv表示结点u和结点v之间的边数(通常为0或1).kukv/2m 表示结点u和v之间期望的边数，ku表示结点u的度数.δsu,sv是克罗内克函数，若结点u，v在同一个簇内，则为1，否则为0.使用模块度来描述得到的聚类结果的紧凑程度.

2.2 GN算法描述

GN算法是由Newman和Girvan两位在2002年提出来的.它是一个经典的基于分裂的社区发现算法.该算法的思想是不断的从网络中移除边介数最大的边，加入模块度[17]Q后其主要流程如下所示：

1) 计算网络中所有边的边介数.

2) 删除网络中边介数最大的边，若出现新的社区，则重新计算模块度Q，记录此时网络结构.

3) 重新计算新的网络的所有边的边介数.

4) 重复步骤2,3，直到网络中每一个结点就是一个社区为止.选取模块度Q值最大时的状态作为该网络的最终状态.

算法流程图如图1所示.

GN算法的准确度较高，但是计算速度慢，边介数计算的开销过大，时间复杂性高，为O(m2n).因此，它只适合处理中小规模的网络.

2.3 GNRA算法描述

GN算法在计算边介数的过程当中，时间复杂度比较高，算法运行效率很低.针对GN算法的缺点，采用链路预测中的RA方法来代替GN算法中的边介数计算，提出了一种基于链路预测的图聚类算法GNRA，算法的时间复杂度得到明显的改善.GNRA算法的主要步骤如下：

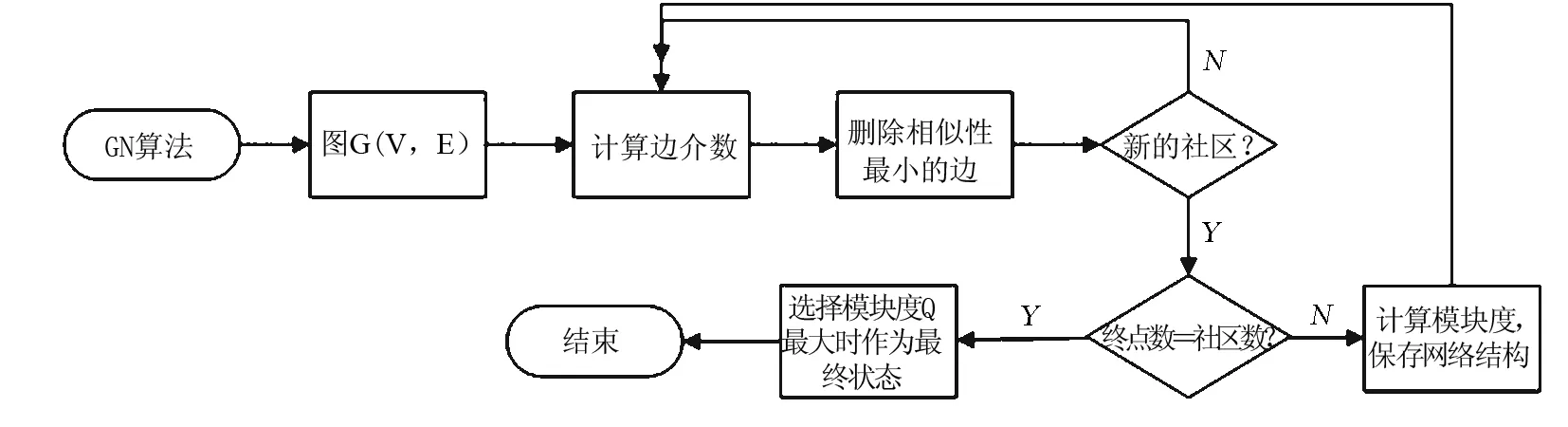
图1 GN算法流程图

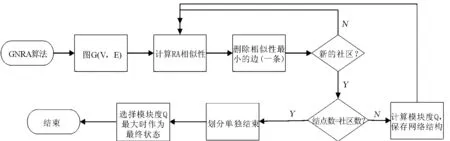
图2 GNRA算法流程图

(1) 计算网络中所有边的相似性g(z)，不相邻的结点之间相似性记为0.

(2) 找到相似性最小的边，并将其从网络当中移除.如果出现新的社区，则计算此时模块度并记录此时社区结构.

(3) 重新计算网络中边的相似性.

(4) 重复步骤2,3，直到每一个结点是一个社区为止.

(5) 将网络中的独立结点进行划分，若仅与一个簇相连，则将该结点加入该簇，若与两个及两个以上簇相连记为中心点，不与任何簇相连记为离群点.

算法流程图如图2所示.

3 IGNRA算法

GNRA算法相对于GN算法时间复杂度得到了降低，但是仍然较高.在实验的过程当中，尝试只计算一次RA相似性，然后逐步的删除相似性较小边的过程.同时发现在计算RA的过程当中，出现了许多拥有相同相似性的边，因此试着同时删除这些边.改进的GNRA算法过程如下：

(1) 计算网络中所有边的相似性g(z)，不相邻的结点之间相似性记为0.

(2) 找到相似性最小的边(边可能不只有一条)，并将其从网络当中移除.如果出现了新的社区，则计算此时模块度并记录此时社区结构.

(3) 重复步骤2，直到每一个结点是一个社区为止.

(4) 划分独立结点：独立结点与同一个簇相连则归入该簇；若与不同簇相连则为中心点；不与任何簇相连则为离群点.

(5) 选择模块度最大的划分作为最终划分.

算法流程图如图3所示.

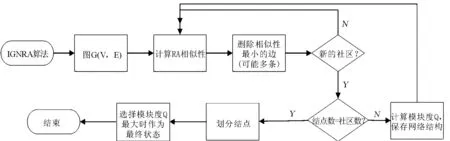
图3 GNRA算法流程图

同GNRA算法相同，给出一个拥有m条边，n个结点的简单图，计算RA相似性所需要的时间复杂度为O(m)，删除边的过程最多需要删除m条边，因此，删除边的过程时间复杂度也为O(m)，因此改进的GNRA算法的时间复杂度为O(m+m)，即为O(m)，该算法的时间复杂度呈线性.

4 实验结果及分析

为了验证提出算法的有效性，实验采用四组常用数据集进行测试，具体数据集见表1.实验环境：处理器为Intel(R)Core(TM)i5-3470，CPU为3.2GHz，内存4GB，操作系统MicrosoftWindows7，使用Java作为编程语言，借助Eclipse开发平台，实现了GNRA算法和IGNRA算法.

表1 常用数据集

数据集结点数边数平均度平均路径长度KDD-toy14253.5712.4zachary-karate34784.5882.4college-football11561310.6612.5football20061807878.7443

首先，分别采用GN算法和GNRA算法对上述数据集进行试验，得到运行时间对比结果见表2.

表2 算法运行时间对比 ms

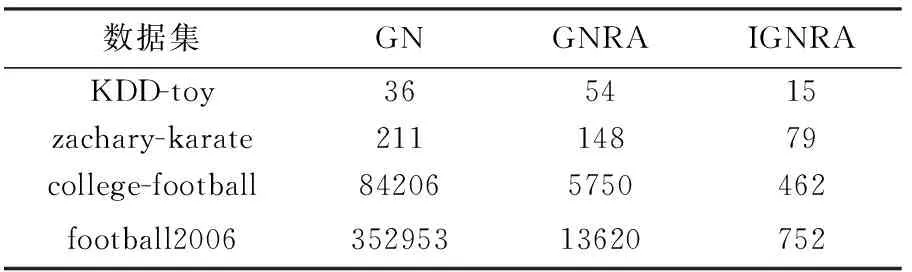
数据集GNGNRAIGNRAKDD-toy365415zachary-karate21114879college-football842065750462football200635295313620752

由以上分析，GN算法与GNRA算法时间复杂度分别为O(m2n)和O(m2)，算法运行时间与边数平方的关系如图4所示.

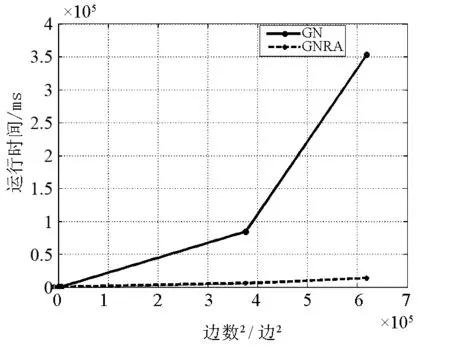
图4 GN与GNRA算法运行时间与边数平方的关系

GNRA算法与IGNRA算法时间复杂度分别为O(m2)和O(m)，算法运行时间与边数的关系如图5所示.

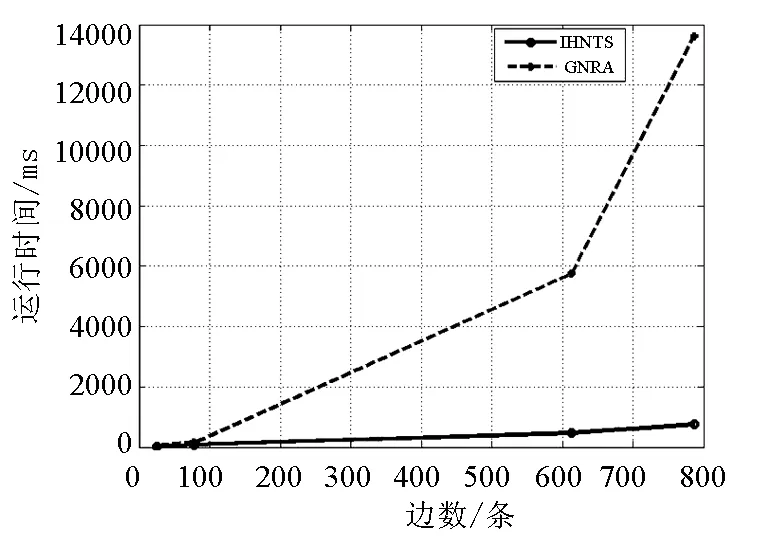
图5 GNRA与IGNRA算法运行时间与边的关系

GN算法计算边介数所需要的时间复杂度为O(mn)，删除m条边所需要的时间复杂度为O(m)，因此总共所需要的时间复杂度为O(m2n).由2.3节知道GNRA算法的时间复杂度为O(m2).由表2及图4可以清楚的看出，GNRA算法相较于GN算法来说，时间复杂度大大降低，其时间复杂度与边的平方成正比.由理论分析、表1、图5可以看出，IGNRA算法时间复杂度得到进一步降低，其时间复杂度与边的数目成正比.因此，从理论与实验上证明了IGNRA算法比GNRA算法具有更低的时间复杂度.

本文采用模块度对聚类结果质量进行度量.一般情况下，一个网络(图)的模块度在0.3～0.7之间，模块度越高，表示聚类的结果越好，簇越紧密.模块度度量结果见表3.

表3 GN算法与GNRA、IGNRA算法模块度对比

数据集GNGNRAIGNRAKDD-toy0.4960.48960.4864zachary-karate0.40980.41110.3914college-football0.59420.59630.5865football20060.58360.56770.5579

由表3可以看出，GN算法与GNRA算法相比，模块度不相上下.GNRA算法与IGNRA算法相比，模块度有所下降.当然模块度高却不一定与真实情况相符，但在一般情况下，真实的聚类结果与模块度最高时相差不大.

5 结束语

针对传统GN算法时间复杂度高的缺点，本文在GN算法的基础上，引入链路预测中RA相似性计算方法，提出了改进的GN算法，称为GNRA算法.并且，对GNRA算法进一步分析，提出了其改进版本IGNRA算法.与GN算法相比，GNRA算法能明显降低时间复杂度，并能够分辨中心点和离群点.同时，通过对模块度的对比，可以发现：GNRA算法得到的簇结构与GN算法得到的簇结构相差不大.而IGNRA与GNRA相比，时间复杂度得到进一步的降低.由于所提算法是利用链路预测中的RA相似性来进行簇划分的，当遇到稀疏图(平均度较低)情况时，划分结果还不甚理想，如何克服这一不足将是下一步的研究重点.

[1] OCHAB J K, BURDA Z. Maximal entropy random walk in community finding[J]. European Physical Journal Special Topics, 2012, 216(1):73-81.

[2] 辛宇, 杨静, 谢志强. 基于随机游走的语义重叠社区发现算法[J]. 计算机研究与发展, 2015, 52(2):499-511.

[3] MORADI P, AHMADIAN S, AKHLAGHIAN F. An effective trust-based recommendation method using a novel graph clustering algorithm[J]. Physica A Statistical Mechanics & Its Applications, 2015, 436:462-481.

[4] 薛洁, 刘希玉. 基于DNA计算的层次图聚类算法[J]. 计算机工程, 2012, 38(12):188-190.

[5] TABRIZI S A, SHAKERY A, ASADPOUR M, et al. Personalized PageRank Clustering: A graph clustering algorithm based on random walks[J]. Physica A Statistical Mechanics & Its Applications, 2013, 392(22):5772-5785.

[6] NEWMAN M E J. Fast algorithm for detecting community structure in networks [J]. Physical Review E, 2004, 69(6):279-307.

[7] XU X, YURUK N, FENG Z, et al. SCAN: a structural clustering algorithm for networks [C].//ACM SIGKDD Intermational Conference on knowledge Discovery and Data Mininy.ACM,2007:824-833.

[8] GIRVAN M, NEWMAN M E J. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(12):7 821-7 826.

[9] TYLER J R, WILKINSON D M, HUBERMAN B A. E-Mail as Spectroscopy: Automated Discovery of Community Structure within Organizations[J]. Information Society, 2005, 21(2):143-153.

[10]戴爱明, 高学东, 王立敏. 一个基于中心度的社团结构发现新算法[J]. 计算机应用研究, 2011, 28(8):2 909-2 911.

[11] 杨文文.基于改进的GN算法的社区发现技术 [D].吉林大学，2012.

[12]于静雯, 杨冰. 基于MapReduce框架下的复杂网络社团发现算法[J]. 微型机与应用, 2014(22):74-76.

[13] ZHOU T, LYU L, ZHANG Y C. Predicting missing links via local information[J]. The European Physical Journal B - Condensed Matter and Complex Systems, 2009, 71(4):623-630.

[14] 吕琳媛. 复杂网络链路预测[J]. 电子科技大学学报, 2010, 39(05):651-661.

[15] 黄立威, 李德毅, 马于涛,等. 一种基于元路径的异质信息网络链路预测模型[J]. 计算机学报, 2014(04):848-858.

[16] 胡文斌, 彭超, 梁欢乐,等. 基于链路预测的社会网络事件检测方法[J]. 软件学报, 2015(9):2 339-2 355.

[17] NEWMAN M E J. Communities, modules and large-scale structure in networks [J]. Nature Physics, 2012, 8(1): 25-31.

(编辑：刘宝江)

A graph clustering algorithm based on link prediction

JIN Chao, ZHANG Long-bo, WANG Lei, AN Jian-rui, HUAI Hao, WANG Xiao-dan

(School of Computer Science and Technology,Shandong University of Technology, Zibo 255049, China)

By redefining how to compute the edge betweenness of the traditional Girvan-Newman (GN) algorithm, a graph clustering algorithm which is named Girvan-Newman algorithm based on Resource Allocation (GNRA) is proposed by using the link prediction. Besides, on the base of analyzing the drawback of the GNRA, the improved Girvan-Newman algorithm based on Resource Allocation (IGNRA), which is the improved version of the GNRA, is also shown. The experimental results on four commonly used groups of the datasets demonstrate that the proposed GNRA algorithm performs better than the traditional GN algorithm in efficiency and the IGNRA has the lowest computation complexity in the three algorithms.

graph clustering; Girvan-Newman algorithm; link prediction;

2016-03-07

国家自然科学基金青年科学基金项目(61502282)

金超，男，jin_chao_hi@163.com; 通信作者：张龙波，男，zhanglb@sdut.edu.cn

1672-6197(2017)01-0017-05

TP301

A