基于可视化编程的计算思维培养模式研究*——兼论信息技术课堂中计算思维的培养

郁晓华 肖 敏 王美玲 陈 妍

（1.华东师范大学 教育学部 教育信息技术学系，上海 200062；2.合肥第四十八中教育集团 滨湖校区，安徽合肥 230000）

基于可视化编程的计算思维培养模式研究*
——兼论信息技术课堂中计算思维的培养

郁晓华1肖 敏1王美玲1陈 妍2

（1.华东师范大学 教育学部 教育信息技术学系，上海 200062；2.合肥第四十八中教育集团 滨湖校区，安徽合肥 230000）

计算思维对信息时代的科技创新和人才创新至关重要，中小学信息技术课堂是计算思维培养的主要落脚点。但是，当前的课堂侧重于技术工具的学习，不利于学生计算思维的发展。可视化编程工具的出现，为计算思维的培养转变提供了新的契机。基于可视化编程的计算思维培养模式，将项目问题的逻辑组织从拆解转变为叠加，并配合教案的引导与学案的支持，可关注到每个学生的思维发展。运用可视化编程工具App Inventor开展该模式的教学实践，实验结果初步显示：学生的计算思维在计算概念水平上整体得到有效提升，在问题解决的形式化和模型化上的改变，也表现明显。该模式的提出和实验验证，可为进一步在中小学信息技术课堂中研究利用可视化编程，培养学生计算思维，提供有效的实践指导。

计算思维；可视化编程；问题探究；App Inventor；人工智能；编程教育

一、时代呼唤计算思维的培养

信息时代的发展，使得数字化和计算化无处不在、无时不有，成为现代社会的基本形态特征[1]，深刻影响着人们的生活方式和思维过程。近年来，计算思维（Computational Thinking）的价值和意义日益突显，成为当前国际计算机界、教育界广为关注的一个热点主题。围绕着科技创新和人才创新，计算思维的培养也成为国际竞争的重要抓手[2]。

计算思维这一概念并不是突然产生的，从古代的算盘，到近代的图灵机，都蕴含其思想。较早加以定义并得到广泛认同的概念，是由美国卡内基·梅隆大学的周以真（Jeannette M.Wing）教授在2006年所提出的，他认为计算思维是运用计算机科学的基础概念，求解问题、设计系统和理解人类行为的一系列思维活动，其本质是抽象和自动化[3]。2012年，美国麻省理工学院媒体实验室（MIT）的lifelong kindergarten group提出了计算思维的三维框架，包括计算概念、计算实践和计算观念三个维度，引发了计算思维实践层面的研究和评价[4]。

计算思维研究和实践已经受到不少国际组织和团体的重视，包括国际教育技术学会 （The International Society for Technology in Education，ISTE）[5]、美国国家计算机科学技术教师协会（Computer Science Teachers Association，CSTA）[6]、美国师生创新技术体验机构 （Innovative Technology Experiences for Students and Teachers，ITEST） 的计算思维工作小组[7]、英国计算机在校工作组 （The UK Computing at School，CAS）[8]、 谷歌计算思维探索团体（Google’s Exploring Computational Thinking，ECT）[9]等。 其中，ISTE和CSTA两家联合给出了计算思维的操作性定义，对计算思维进行问题解决的过程进行了表述；CAS作为信息技术的学科协会，与其他机构合作设计信息技术课程，阐述了计算思维的人机交互特点和综合能力体现；ITEST在分析大量计算思维培养案例后，提出的“使用—修正—创造”培养框架被广泛推行；ECT在计算思维的认识中引入了技术支持下的问题解决过程，并提供大量培养计算思维的资源，致力于在K-12阶段开设课程，以培养学生的计算思维能力。

相对于国外，目前，国内在计算思维的研究上还比较多侧重于概念层面的探讨。王荣良教授较早在分析和总结国内外对计算思维的理解的基础上，提出了计算思维就是通过约简、嵌入、转化和仿真等方法，把一个看来困难的问题，重新阐述成一个人们知道怎样解决的问题[10]。后来，随着研究的不断深入，计算思维被认为是一种反映计算机技术本质特征和解决问题的核心方法，能提升学生的计算素养，培养学生用计算机处理和解决领域问题的思维方法和表达形式[11]。

2016年，我国的《高中信息技术课程标准修订稿》明确指出，计算思维是学科的核心素养之一，是指能够采用计算机领域的学科方法界定问题、抽象特征、建立结构模型、合理组织数据；通过判断、分析与综合各种信息资源，运用合理的算法形成解决问题的方案；总结利用计算机解决问题的过程与方法，并迁移到与之相关的其他问题解决过程中。具体表现为解决问题过程中的形式化、模型化、系统化、自动化[12，13]。

由上阐述，我们可以发现，自计算思维这一概念被明确提出后，多年来，国内外的学者或组织对其内涵不断加以明晰，对其外延不断加以丰富，提出了不同的见解，开展了多样化的实践。其共同之处在于：将思维过程与技术工具相互结合，形成了技术支持下的问题解决过程与方法，并实现在计算机学科领域以外的扩展与推广，被看作是当今创新人才必备的重要素养。

二、可视化编程与计算思维培养的转变

（一）当前信息技术课堂在计算思维培养中存在的问题与不足

计算思维的培养研究，早期比较多落脚于高等教育领域中的计算机学科。但随着计算化思想与方式的不断渗透，计算思维作为一种顺应网络时代发展的普适技能[14]，其培养目标被纳入中小学信息技术教育，成为一种必然趋势[15]。

早在2011年，美国就将计算思维纳入其《CSTAK-12 标准（修订版）》中；随后，2013 年英国、2015年澳大利亚，也都将计算思维作为新信息技术课程计划的重要内容。在国内，信息技术课程同样是培养中小学生计算思维的主要途径。在新修订的《高中信息技术课程标准》中，明确指出：信息技术课程要帮助学生学会运用计算思维识别与分析问题，抽象、建模与设计系统性解决方案[16]。

在当前中小学信息技术课堂教学中，不少一线教师在涉及一些程序设计、算法编程类的内容单元上，大胆渗透了计算思维的培养和实践。最常用的方法包括项目式、主题式、范例式、游戏式等等。尽管这些教学方法设计意图良好，教师运用时也各不相同，但由于在大多数情况下受制于教学内容的约束或教学目标的完成，难以很好支持深层次计算思维培养目标的实现。

究其原因，我们认为，一方面，是教师对计算思维的认知不够，对课标的理解仅停留于表面；另一方面，教师也缺少计算思维扎根于课堂教学的理论与方法指导[17]。因此，当前信息技术课堂在培养计算思维方面，存在以下问题与不足：

第一，侧重编程工具的学习。在算法和程序设计的课程中，教师多采用一些编程工具来帮助学生完成学习内容。工具使用的作用本是为了达到辅助学生完成任务，从而达到思维和能力不断提高的目的。但在实际的课堂中，由于课时量少、要求水平高等硬性规定，造成教师在教学时，更加关注学生任务完成的基本要求，而无法达到对学生思维能力的进一步提炼。

第二，教师预设解题路径。为了确保问题解决的成效，教师通常会事先将整个问题的设计思路和步骤剖析出来，然后要求学生根据这些步骤依次完成任务，从而结束整个项目。这样的教学方法，通常会给学生一种错觉——自己的学习任务就是完成教师所规定的解题路径，并不需要自己深入去探索、去创新，因而，对学生的思维能力培养反而起到了一种阻碍的作用。

第三，过于关注个别先进的学生。思维培养存在着极大个体差异，但采用统一的教学思路和评价尺度，不可避免只有部分“适配”学生能够从中获益，尤其是那些比较主动或学习优秀的学生。在常开展的一些项目活动中，通常小组核心成员的思维比较能够在教师的有效关注下得到较好地发展，而相对活跃度较差的学生往往会由于教师的无暇顾及而被“放羊”，从而造成一个班级学生的计算思维培养处于一种“差别对待”的发展状况。

（二）可视化编程带来的转变契机

所谓可视化，就是把数据、信息和知识等抽象内容，以直观可视的方式表达出来，并对数据进行更深层次的认识和解读[18]。可视化也是近年来的研究热点，在视觉文化以及计算机科学领域图形图像技术发展的影响下，可视化的研究受到越来越多的关注。编程就是让计算机为解决某个问题而使用某种程序设计语言所编写的程序代码，并最终得到相应结果的过程。可视化与编程相结合所产生的可视化编程，则是一种全新的程序设计方法，它以“所见即所得”为原则，规避抽象、繁琐的程序语言编写，仅通过直观的操作方式，即可像搭积木式地构造出应用程序的各种界面和逻辑，并保证程序与结果的同步调整。

可见，可视化编程的优势主要体现在以下几个方面：第一，可视化编程的直观操作和趣味体验，能有效提升学生的学习兴趣；第二，封装和简化的编程逻辑能加快开发速度，规避繁琐的语法调试；第三，降低代码语句编写等基础性技术门槛，可有效聚焦于计算思维的培养和能力的发展。

在中小学信息技术课上，较常用到的可视化编程工具有 Scratch、App Inventor、Alice、Daisy、the Dinosaur、Hackety-Hack、Code Monster 及 Codecademy等。本研究借助的可视化编程工具为App Inventor，它是谷歌公司开发的一款在线Android可视化编程工具软件，用户通过图形化积木式的拖放组件，便可完成Android移动软件的开发。

目前，基于可视化编程开展计算思维的培养，在国外的研究和实践较为广泛。比如，美国麻省理工学院媒体实验室 （MIT）的lifelong kindergarten group所开发的旨在课堂中培育计算创意能力、基于计算思维三维框架的Scratch创意计算课程中[19]，教师作为引导者，学生以设计者和创造者的身份通过亲自动手探究，投入到设计创意活动中，并在过程中逐步发展计算思维、掌握计算概念并内化为计算策略。课程主要使用的评价方法有：作品档案袋分析法、基于编程制品的访谈法、情景设计法等。

在欧盟的波兰，有100多所学校展开的Coding School项目所设计的基于Scratch的课程[20]，采用基于问题的教学模式，在帮助学生了解游戏规则、完成任务中发展学生的思维，进行创造性的思考活动；在教师的组成上，不仅有计算机学科教师，还有其他学科教师，使得计算思维的培养与多个学科相结合。

此外，一些网络平台也提供了大量计算思维与学科教学整合的案例、相关的学习资源以及关于计算思维的评价方式。如，美国俄勒冈大学制作的一个用于向中小学生介绍计算思维概念在线网站Thinking myself以及目前在美国教授计算思维使用最广泛的在线资源Code等网络平台。

从上述这些实践和研究中，我们总结出基于可视化编程的计算思维培养的一些相同点：

第一，在教学模式上，注重培养学生解决问题的能力。采用基于项目的学习，教学由简到繁，逐步展开；每个开发项目与一定的情境与故事相结合；可视化编程工具作为解决问题的辅助手段，以问题的解决为最终目标而非简单的工具使用教学；学生在学习活动中占有主导地位，教师的作用主要为引导学生解决问题并培养学生的计算思维能力；在学习过程中，以学生独立完成各项任务为主。

第二，计算思维的培养并不仅限于信息技术学科，它往往与多个学科相结合，与STEAM教育相结合，是一种综合性的学习。

第三，在计算思维培养的评价方面，采用过程性评价和总结性评价等多种评价方式相结合。而通常学生的作品与其运用计算思维解决问题相关，因此，通过访谈等形式可了解学生在项目开始、进行、结束等整个过程中的经历，关注学生计算思维发展的趋势以及最终的计算思维水平。

第四，计算思维培养的主要场所为中小学和幼儿园。

三、基于可视化编程的计算思维培养模式

（一）不同视角下的计算思维培养模式

基于对计算思维的不同理解视角，现有关于计算思维的培养模式，主要可分为以下三种：

模式1.从人机交互的视角[21]

这一视角将计算思维看成是人与计算机之间的反复交互过程。因此，就存在输入与输出两种角色。而计算思维的形成，就体现为将人将对问题的认知（抽象和形式化）输入计算机设备，通过信息处理过程（复杂数据的呈现以及事实和关系知识的存储）加以输出。这一模式强调对问题抽象和形式化过程的思维可视化呈现。

模式2.从概念内涵的视角[22]

这一视角将计算思维看成是学科思维和计算哲学之间的一种联结。对计算思维的培养着重从思维的结构化、形式化、最优化、关联与交互、重用与共享五个核心要素，分别加以落实，并通过一定的计算工具与方法展开和呈现。

模式3.从工程设计的视角[23]

这一视角强调计算思维参与解决问题的过程。计算思维的培养可分为：识别问题与需求、研究问题与需求、开发可能的解决方案、选择最可能的解决方案、构建原型、测试和评估解决方案、沟通解决方案、重新设计8个步骤。其中，步骤1-3组成模型的分析部分，步骤4-5为综合部分，步骤6-7为评价部分。

由上阐述不难看出，这三种模式在实践层面各有侧重，模式1提出了计算思维发展呈现和观测的思路，模式2指出了计算思维培养的五方面内容以及对应的计算工具与方法，而模式3则给出了计算思维培养活动需要开展的八个环节。这些研究可分别从评价、内容和活动三方面，为我们开展计算思维培养模式的设计提供了借鉴。

（二）基于可视化编程的计算思维培养新思考

可视化编程工具除了能作为支持学生计算思维输出与呈现的媒介以外，还因其直观易学、开发迅速等优势，使得教学活动可以更加关注于学生对问题的解决，从而强化对计算思维的培养。因此，针对当前信息技术课堂中计算思维培养存在的问题与不足，我们在现有计算思维培养模式的基础上，提出以下新的思考：

1.项目问题逻辑的组织从拆解转变为叠加，适配学生的个体差异

以往开展的大多数主题/项目式教学中，教师一般会预先给学生呈现整个情境、复杂完整的问题域和最终的结果目标，接着再将这一复杂情境进行拆解，分解成一个个更小单元、较为简单的问题任务，并提供相应的解决思路或方法；而学生的主要任务就是完成教师所拟定的统一化解题路径，理解教师对问题的分析和解决逻辑。

但在本研究的教学设计中，主题或项目将从最底层、最基础的问题单元出发，一开始并不展现给定情境的完整问题域；教师在教学过程中，根据学生对问题的理解和加工情况逐步加以引导、叠加，拓展情境的问题域，提升任务的复杂度；由于整个问题解决的过程放权给学生自主探索，因此，最终的结果也将根据学生不同的能力和想法而呈现出不同的效果。这样一来，项目问题逻辑的组织就从教师的拆解转变为学生的叠加，需要学生更多的思维参与，而整个学习不再以预先拟定的结果为目标后，教师也能够更好地关注学生在问题解决过程中的思维培养。

2.教案的引导和学案的支持

教案为教师提供主题/项目的教学路径，与传统的信息技术课程相比，本研究中的教案设计要求教师在教学过程中更加关注学生的思维发展。教案由多个问题活动组成，从简单问题开始，复杂度逐层叠加，指向不同计算思维的发展。每个活动包含基本的问题解决路径、涉及的知识点以及计算思维培养要点。在教学过程中，所提供的解决路径只是作为引导和参考，并不限制学生的多元化解决思路。教师通过师生互动，指导学生掌握解决问题的思路与方法，而不是简单的工具讲解；教师随时引导学生对问题进行深入思考和模式迁移，并鼓励学生自己利用可视化编程方式加以实践检验，从而促进计算思维在解决问题过程中形式化、模型化到自动化的发展。

学案作为一种启发性支架，协助教师支持学生的自主探索与自我的问题解决。学案以问题为基础，从问题界定、特征抽象、模型构建和问题迁移等方面，引导和记录学生个性化方案的探索过程。同时，学案还强调思维的及时强化与反思，协助学生在完成阶段性任务后对所学内容进行总结、抽象和内化。

（三）基于可视化编程计算思维培养模式的建构

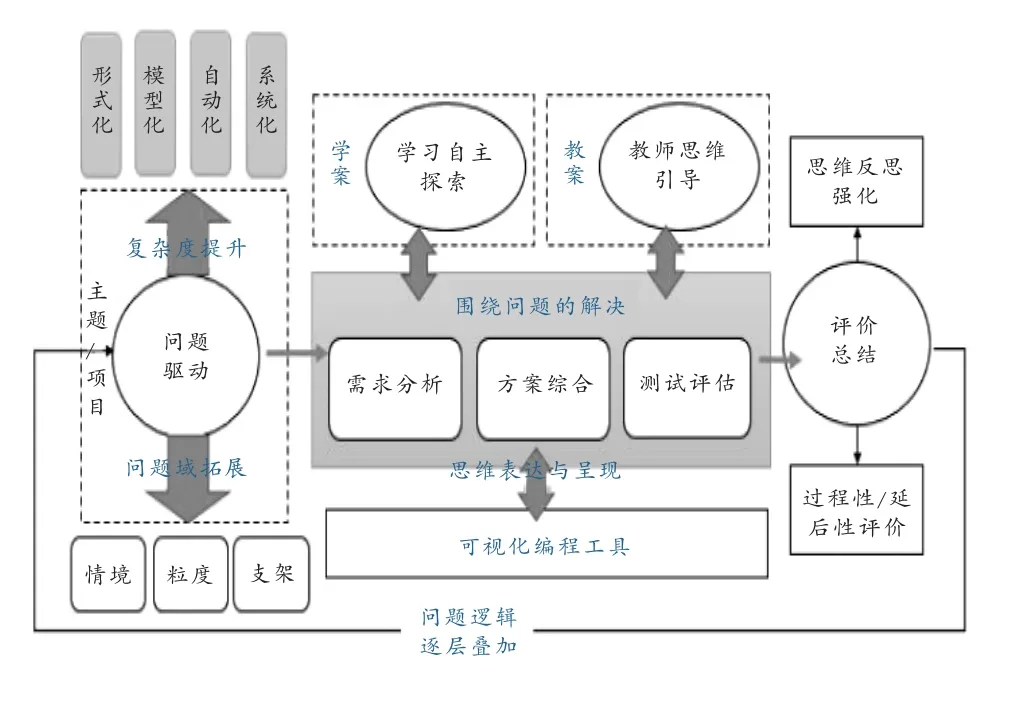
图1 基于可视化编程的计算思维培养模式

综上，本研究所提出的基于可视化编程的计算思维培养模式如下图1所示。它围绕主题/项目问题的解决，通过需求分析、方案综合和测试评估环节，学生计算思维的发展不断在与可视化编程工具的交互中得以表达和呈现，进而加以评价；配套教案和学案的应用与支持，问题逻辑的逐层叠加与学生的差异化相适配，学生在解决问题的过程中实现计算思维形式化、模型化到自动化的发展。

在具体的实施过程中，我们认为，该模式还需要以下观念上的转变：

1.既要发挥教师的主导作用，又要关注学生的自主发展

教师的主导作用虽然常常被批判忽略了学生的主动性，但它可有效保证教学的进度和节奏。因此，为了使学生计算思维的培养能在课堂有限的时间内快速产生效果，本模式在充分发挥教师在任务主线和目标进度上主导优势的基础上，让学生同时也拥有更多的学习自主权。即对于课堂中教师所提出的问题或布置的任务，学生可结合自身的生活体验和实践经验，提出新方法和新思路，而不是像以往一样，仅是对教师示范案例的接受与模仿。

2.在支架的支持下，问题任务以个体解决为主，小组协助为辅

主题/项目式教学方法的开展，通常需要建立学习小组，形成分工，共享成果。在这一规则下，个体的发展服从于集体的利益，但这并不利于计算思维对差异化培养的需求。而在本模式的教学实践中，要求教师提出的问题任务，首先要以学生自主探索为主，并安排专门的环节和时间让学生进行独立思考，在一定的支架支持下，提出自己的解决思路，同时也鼓励学生之间的协助互动。小组协助在本模式中只是作为辅助手段，以便利用学生间的学习进度差距，弥补教师在课堂中无法及时反馈每个学生的不足。

3.问题源自于学生已有的生活体验，且注重恰当的任务划分粒度

在本模式中，每一个任务活动都由一个问题情境驱动，而只有来自于学生已有生活体验的问题，才能有效引起学生的共鸣，激发他们主动将问题与已有的知识和经验联系起来，进而产生探索的兴趣，以及解决问题的愿望。但要有效促进学生计算思维的发展，问题任务粒度的划分至关重要，需要确保在一定挑战性基础上的复杂度逐渐提升，符合学生现有认知水平和实际解决问题能力，让学生能够在一种“舒适”的压力环境下，在给定的时间内有效完成任务。即学生在主题/项目的每个阶段，都能获得一种成就感的体验。同时，教师还要能在教学过程中根据学生的思维发展动态，为不同学生调整恰当的问题粒度。

4.通过过程性评价和反馈性评价，关注学生对问题的思索与创新以及思维的迁移与发散，允许延后性的成果反馈

相对于以往模式对任务结果的看重，本模式关注的是过程性评价，并同时辅于反馈性评价。即通过学生对自我发展的反思，监控学生对于问题的思索过程，以及伴随着他们计算思维的发展状况，尤其是在解决问题的迁移、发散以及创新方面。此外，由于问题域的逐层拓展以及复杂度的逐层提升，随着基础的夯实，后期任务的解决，会反过来为前期任务的解决带来新的思路和途径。因而，在本模式中，我们允许延后性的成果反馈，即重新评价学生先前的表现，以鼓励学生进行再创造的思维能力发展。

四、教学实践的应用与验证

为了验证可视化编程支持下计算思维培养模式的有效性，本研究设计了基于App Inventor的计算思维培养的教学实践。它共有五个主题项目活动组成，并配套开发了相关的教案与学案；然后，在上海某中学开展了一个学期的拓展课教学；课程结束后，我们对计算思维的培养效果，从计算概念和解决问题维度进行了评价与分析。

（一）项目案例

这里以“躲避障碍物”游戏项目为例。该游戏的情境中包括小球、障碍物和非障碍物，学生需要识别情境中对象间的相互关系，设计碰撞规则来制订游戏机制；然后，利用App Inventor工具加以实现。在此过程中，学生在教师的引导和学案的支架下，完成自身计算思维的发展，提升解决问题的能力。

1.问题设计

如图2所示，学生首先要分析具体问题，思考解决方法，然后利用App Inventor工具，选择合适的组件和算法逻辑来验证解决方案。伴随着问题的叠加、复杂度的提升，计算思维的培养也得到发展；解决上一个问题，会对下一个问题的解决提供经验和技术方法。学生的计算思维发展，从计算概念维度主要表现为算法思维、纠错思维、逻辑思维、抽象思维四方面内容；从解决问题维度可分为形式化、模型化、自动化、系统化四个层次。

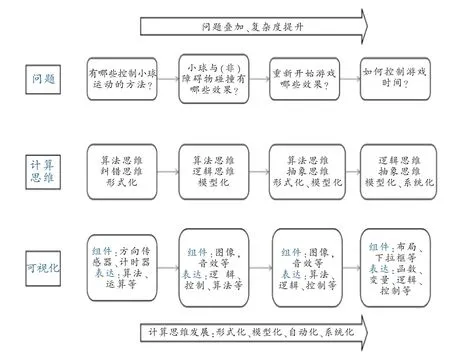
图2 “躲避障碍物”的问题设计

2.教案设计

教案设计围绕计算思维的发展，包括教师活动、学生活动、知识内容和思维评价四个部分。教师活动与学生活动相辅相成，由问题驱动。教师活动为教师课堂上讲解知识、引导学生进行自主探究，包括讲解、提问、操作和要求等；学生活动为教师活动后的学生反馈，包括观察、回答、操作、填写、作图等；知识内容分为问题背景、工具操作和思维知识三类；问题背景为教师提供主题/项目相关的背景知识，提出解决问题的参考路径；工具操作指完成任务所需App Inventor工具软件的操作设置，供教师参考；思维知识为完成问题任务所需具备的基础计算概念，需要教师着重关注并加以引导；思维评价从解决问题维度给出了针对学生计算思维发展的评价量规。

教案设计总体上提供了教师基本的授课思路与资源，但教师应根据学生思维发展的反馈情况灵活进行调整，随时鼓励学生对问题进入深入思考和模式迁移。

3.学案设计

学案设计围绕问题的解决，包括主题思考、自我检查和主题测试三个部分。主题思考通过一定的支架，提示引导学生自主探索，将问题解决方案用流程图的方式加以表达，并用App Inventor实践加以检验。自我检查强调思维的及时反思与强化，帮助学生回顾课堂知识并促进学生对计算概念的理解。在每一个项目教学结束后，要进行主题测试。主题测试围绕该项目能否帮助学生总结问题的解决思路，拓展和迁移到实际学习或工作情境中。

（二）实验过程

为期一个学期的拓展课教学实践，共有30名中学生（六年级：15人，七年级：10人，八年级：5人）参加，五个项目共授课48课时，每周4个课时。为了检测可视化编程对学生计算思维培养的影响，本研究首先从计算概念的四个方面，在课程教学前后分别对授课学生进行了前、后测试，评价他们在这四个方面的发展情况。然后，从解决问题的形式化和模型化维度，在教学的第四个项目，即“躲避障碍物”游戏教学前后对授课学生进行前、后测试，采用流程图法对测试结果进行评价和分析[24]。在授课过程中，还通过观察与对话，从质性研究角度对比学生前后认知结构和态度情感的变化。

（三）验证数据

1.计算概念的维度

在参加课程学习的30名学生中，有28名（六年级：13人，七年级：10人，八年级：5人）有效参加了计算概念的前、后测试问卷。其中，计算概念的测试共设置有11道题目，编号4、5题测试抽象思维，编号6、7、13题测试算法思维，编号8、9、10题测试纠错思维，编号11、12、14题测试逻辑思维。最终的前、后测试结果如表1所示。

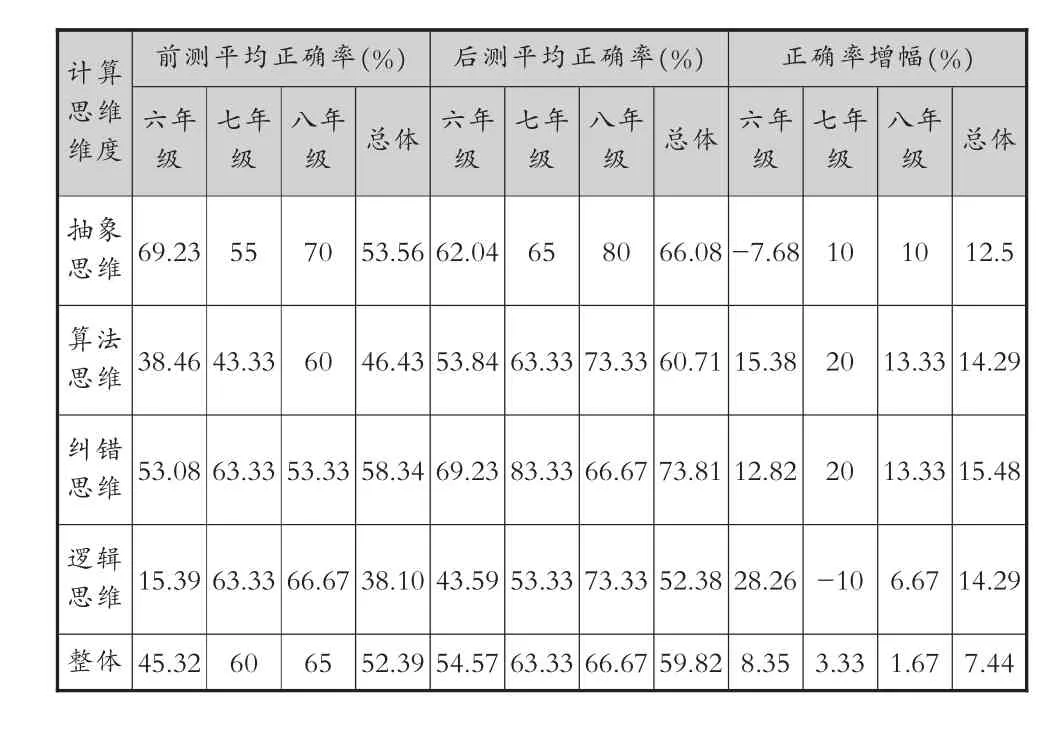
表1 抽象、算法、纠错、逻辑思维前后测对比

从整体来看，学生的计算思维水平均得到了有效提升，其中六年级最为显著。在抽象思维方面，七、八年级的发展比较明显；在算法思维和逻辑思维方面，七年级的发展相对六、八年级更加明显；在逻辑思维方面，六年级的发展最为突出。

我们分析认为，出现年级差异的原因可能是：（1）六年级学生计算思维的起点能力低于七、八年级，所以其发展空间更大；（2）课程难度和授课节奏的设置更适合六、七年级的学生，对于八年级而言，问题任务的挑战性可能不够。

2.解决问题的维度

在进行“躲避障碍物”项目教学前，前测任务要求学生在描述“躲避障碍物”游戏情境的前提下，尽可能多的抽取游戏规则，画出规则的操作流程图，最后，根据流程图进行算法设计。后测任务与前测一样，但会根据学习任务的完成情况，对完成较差的学生使用与“躲避障碍物”游戏类似的“小车快跑”游戏情境，而完成较好的学生则使用复杂度提升后的“开心弹珠”游戏情境。

同类型游戏情境在对象和游戏规则方面相似，可考察学生是否能完成简单的问题，解决思维迁移；而拓展型游戏情境，在对象识别和关系识别上存在较大差异，可测试学生能否完成复杂的问题，解决思维拓展。在参加课程学习的30名学生中，有24名（六年级：13人，七年级：8人，八年级：3人）有效参加了该测试，最终5名学生进行了同类型后测，19名进行了拓展型后测。前、后测验从解决问题的形式化和模型化维度评价计算思维的发展，结果分析如下：

（1）形式化。通过测试学生识别问题情境里的对象及对象间的关系情况，可考察学生界定问题、抽象特征、形成关系的能力，即解决问题过程中的形式化能力。如图3案例所示，某学生虽能识别“躲避障碍物”游戏情境中的对象，但还未形成完整的对象关系，因而，在设计游戏操作时，还不能完整表达对象之间的游戏逻辑；而在“开心弹珠”游戏中，学生则能利用“然后”、“如果……则”等逻辑语言完整表达游戏对象间关系，说明该学生在教学后，其抽象特征、形成关系的能力得到了一定改善。

图3 某学生前后测对象识别对比

“躲避障碍物”游戏情境包含八种关系，“小车快跑”包含七种关系，“开心弹珠”包含六种关系。假定学生识别游戏情境中关系的数量为N，那么关系识别比例T的计算公式如下：

我们观察发现，通过教学后，同类型后测中有3名学生能识别对象、形成更多的关系，拓展型前后测中有13名学生能识别对象、形成更多的关系。总的来讲，在“躲避障碍物”项目教学后，有2/3的学生在解决问题中的形式化能力有所提高；而在年级差异表现上，七、八年级的表现明显要优于六年级学生，说明计算思维的形式化能力，在高年级学生中更容易得到锻炼。

（2）模型化。通过测试学生能否根据对象间的关系完成游戏机制流程图的设计，可考察学生形成关系机制、建立结构模型的能力，即解决问题过程中的模型化能力。流程图采用打分方式进行评价，满分为10分。评分标准包含两条：第一，观察流程图是否能完整表达学生描述出的对象间关系；第二，观察该流程图是否存在逻辑错误。

如图4案例所示，某学生在“躲避障碍物”游戏的流程图上，未能描述所有的游戏功能，①和②处逻辑上不完整，没有体现输赢的条件，游戏机制含糊不清；而在“开心弹珠”游戏的流程图中，不仅描述了所有游戏功能，建立了③和④处完整的逻辑和关系机制，还通过⑤处的补充，让整个游戏机制更加完善，说明该生在教学后，形成关系机制、建立结构模型的能力有所提升。

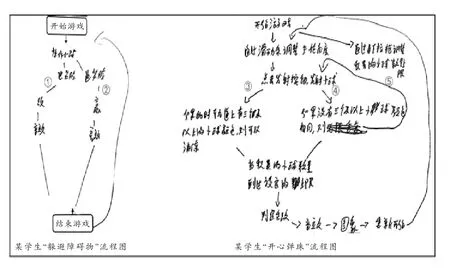
图4 某学生前后测流程图对比

经统计，通过教学后，同类型前后测有3名学生，拓展型前后测有11名学生在流程图设计能力方面有所提高。总的来讲，通过“躲避障碍物”项目教学后，超过一半的学生在解决问题过程中的模型化能力有所提升；而在年级差异表现上，七、八年级的表现同形式化一样明显要优于六年级学生。同时，我们在流程图分析中，还发现以下两种情况：第一，大多数学生在拓展后测流程图制作中，会对已经形成的关系进行补充，说明他们开始从模型构建的完备性和合理性角度，审视问题域中的对象关系，并对不合理的地方进行补充修改。第二，大部分学生能在流程图中画出判断、选择和循环的过程，但在最后的算法设计部分，学生往往只能表达出判断和选择过程，还无法表达循环过程。

3.观察分析

基于可视化编程的计算思维培养模式，要求学生提出不同于教案设计的方案，也可对已有方案提出质疑并进行自主修改。在实验教学过程中，我们研究观察发现：有的学生在完成小球与障碍物碰撞效果的任务后提出，是否可以设计其他的碰撞效果让游戏变得更复杂、有趣？还有的学生针对“开始游戏”功能部分的游戏机制，提出了自己的设计方案。这些现象显示，学生开始从被动的接受知识转向自主探索学习，通过判断、分析与综合各种已有信息资源，对已有的设计进行修改，并尝试运用合理的算法形成解决问题的方案，体现了计算思维能力的提升。但在研究中，学生迁移能力的培养仍然不足，解决问题的系统化能力还有所欠缺。

五、总结与展望

今天的社会正发生着以数据与信息科技为驱动的深刻转变，未来已来，随着人工智能的发展与应用，人们也越来越多通过这些数据与信息认知并改造整个世界。只有积极将计算思维作为人才培养的重要组成部分，才可确保下一代在人工智能时代的创新动力。为此，国家最近在《新一代人工智能发展规划》中，也提出要在中小学等实施计算机编程方面的教育。

2017年《地平线报告（基础教育版）》指出，计算思维应该是阅读、写作、计算之外的另外一项必须熟练掌握的基本技能，如何培养中小学生的计算思维，无题是21世纪一个重要的课题。目前，无论是计算思维还是编程教育，国内这一研究仍然处于起步阶段[25]。而本研究所提出的培养模式和所开展的教学实践，可在一定程度上支持这一领域的研究发展。

本研究所提出的培养模式转变了以往思路，充分利用了可视化编程操作直观有趣，开发快速简捷等优势，使得信息技术课堂教学能更为有效聚焦并支持计算思维的发展。新模式建议问题情境要来源于学生已有生活体验，问题域以恰当的粒度进行叠加勾勒；在问题解决过程中，以个体解决为主，给予学生一定的支架和充分的自主探索空间来发展思维能力，而教师从旁引导以保证课堂的进度与节奏；关注学生计算思维的过程性发展与评价，要有机与反馈性评价和延时性评价相结合。

虽然研究所开展的实践存在着实验对象数量较少、类型单一、时间较短等问题，但应用结果初步显示所提出模式的合理性与有效性。在之后的研究工作中，我们将会进一步调整实验对象的规模与类型、实验的过程与方法，逐步完善和优化计算思维培养模式的操作细节和相关资源，从而使得这一教学模式对中小学信息技术课程教学实践更具参考价值。

[1]任友群，隋丰蔚，李锋.数字土著何以可能?—也谈计算思维进入中小学信息技术教育的必要性和可能性[J].中国电化教育，2016（1）：2-8.

[2]教育部高等学校大学计算机课程教学指导委员会.计算思维教学改革宣言[J].中国大学教学，2013（7）：7-10.

[3]Wing J M.Computational thinking[J].Communications of the ACM，2006，49（3）:33-35.

[4][19]Brennan K，Resnick M.New frameworks for studying and assessing the development of computational thinking[C].Vancouver，Canada:Proceedings of the 2012 Annual Meeting of the American Educational Research Association，2012:1-25.

[5]国际教育技术学会（The International Society for Technology in Education，ISTE）[EB/OL].[2017-10-12].https://www.iste.org/explore/categorylist?code=Computational+thinking.

[6]美国国家计算机科学技术教师协会（Computer Science Teachers Association，CSTA）[EB/OL].[2017-10-12].https://www.csteachers.org/page/CompThinking.

[7]美国师生创新技术体验机构（Innovative Technology Experiences for Students and Teachers，ITEST）[EB/OL].[2017-10-12].http://stelar.edc.org/publications/computational-thinking-youth.

[8]英国计算机在校工作组（The UK Computing at School，CAS）[EB/OL].[2017-10-12].http://community.computingatschool.org.uk/resources/252.

[9]谷歌计算思维探索团体（Google’s Exploring Computational Thinking，ECT）[EB/OL].[2017-10-12].https://edu.google.com/resources/programs/exploring-computational-thinking/.

[10]王荣良.计算思维对中小学信息技术课程的影响初探[J].中国教育技术装备，2012（27）：56-57.

[11]吴明晖.面向计算思维的App Inventor课程建设与实践[C].全国高校计算机网络教学暨网络工程专业建设研讨会，2014.

[12]任友群，黄荣怀.高中信息技术课程标准修订说明[J].中国电化教育，2016（12）：1-3.

[13][16]李锋，赵健.高中信息技术课程标准修订:理念与内容[J].中国电化教育，2016（12）：4-9.

[14]李艳坤，高铁刚.基于思维视角的计算思维综合解读[J].现代教育技术，2017（1）：68-73.

[15]Lye S Y，Koh J H L.Review on teaching and learning of computational thinking through programming:What is next for K-12?[J].Computers in Human Behavior，2014，41:51-61.

[17]王荣良，卢文来.计算思维—行进中的挑战[J].中国信息技术教育，2017（6）：4-10.

[18]李芒，蔡旻君，蒋科蔚，王妍莉.可视化教学设计方法与应用[J].电化教育研究，2013（3）：16-22.

[20]Kalelioglu F， Gülbahar Y， Akcay S， et al.Curriculum integration ideas for improving the computational thinking skills of learners through programming via scratch[C].Local proceedings of the 7th international conference on informatics in schools:Situation，evolution and perspectives，2014:101-112.

[21]Cooper S，Prez L C， Rainey D.Education k-12 computational learning[J].Communications of the ACM， 2010，53（11）:27.

[22]Wenchong S， Maohua L， Hendler P.Computational features of the thinking and the thinking attributes of computing:on computational thinking[J].Journal of Software （1796217X）， 2014，9（10）:2507-2513.

[23]Massachusetts Department of Education.Massachusetts science and technology/engineering curriculum framework[EB/OL].[2017-09-07].http://www.doe.mass.edu/frameworks/scitech/1006.pdf.

[24]Bienkowski M，Snow E，Rutstein D W，et al.Assessment design patterns for computational thinking practices in secondary computer science:A First Look[J].Technical Report，2015.

[25]NMC Horizon Report 2017 K-12 Edition[EB/OL].[2017-09-07].http://www.nmc.org/publication/nmccosn-horizon-report-2017-k-12-edition/.

Research on the Model of Developing Computational Thinking based on Visual Programming：Also on the Cultivation of Computational Thinking in Information Technology Classroom

Yu Xiaohua1， Xiao Min1， Wang Meiling1&Chen Yan2
（1.Department of Education Information Technology， Faculty of Education，East China Normal University， Shanghai 200062；2.Hefei Forty-eighth China Education Group Binhu Campus，Hefei Anhui 230000）

Computational thinking is crucial to technological innovation and personal innovation in the information age， and the information technology class in primary and secondary schools is the main foothold of cultivating computational thinking.However， current classes focus on the learning of technical tools and are not conducive to the development of students’ computational thinking.The emergence of visual programming tools provides a new opportunity for the training of computational thinking.This paper proposes a model of developing computational thinking based on visual programming.With the support of the teaching plan and learning plan，this model transforms the logical organization of the project from disassembly to overlay and fits individual differences to concern every student’s computational thinking development.By using App Inventor， which is one of visual programming tools， to carry out the teaching practice based on this model， the experimental results preliminary show that students’ computational thinking has been effectively promoted in terms of computational concepts and the changes in formalization and modeling of solving problems are also obvious.Through proposing this model and verifying its validity，some feasible research ideas for further studies by using visual programming to cultivate students’computational thinking are provided.

Computational thinking；Visual programming；Problem solving；App inventor；Artificial intelligence；Programming education

G434

A

1672-0008（2017）06—0012—09

本文系全国教育科学 “十二五”规划2013年度教育部重点课题 “智慧教育视域下学习活动流及其信息模型建构与应用”（编号：DCA130222）研究成果。

郁晓华，博士，华东师范大学教育信息技术学系副教授，主要研究方向：信息化教与学、学习技术系统设计与开发、个人学习环境设计开发、学习分析与可视化；肖敏，华东师范大学教育信息技术学在读硕士研究生，主要研究方向：学习分析与可视化；王美玲，华东师范大学教育信息技术在读硕士研究生，主要研究方向：个人学习环境设计开发；陈妍，合肥市第四十八中学滨湖校区数学教师。

2017年9月8日

责任编辑：陶 侃