考虑弯曲转角的框剪结构-TMD减震体系数值优化设计

贺 辉，谭 平，刘良坤

（1.广州大学工程抗震研究中心，广州 510405；2.北京工业大学建筑工程学院，北京 100124）

考虑弯曲转角的框剪结构-TMD减震体系数值优化设计

贺 辉1，谭 平1，刘良坤2

（1.广州大学工程抗震研究中心，广州 510405；2.北京工业大学建筑工程学院，北京 100124）

提出了一种适用于框剪结构的TMD减震体系优化设计方法。将结构简化为连续-离散的悬臂梁模型，该模型不但能体现结构的剪切变形，而且能充分考虑结构弯曲变形产生的弯曲转角对TMD动力特性的影响。使用Rayleigh-Ritz法分析结构动力特性，在此基础上，基于结构的性能目标使用遗传算法对TMD体系进行数值优化设计。最后，针对某框剪结构的TMD减震体系优化设计问题进行了研究，研究结果证明了将TMD质量比作为优化参数的正确性。通过与传统Den Hartog参数对比发现，此方法设计的TMD质量更小且控制效果更好。

框剪结构；TMD；Rayleigh-Ritz法；层间位移角；遗传算法

0 前言

TMD作为一种被动控制装置可以有效应用于结构振动控制[1-2]。Den Hartog给出了结构无阻尼情况下TMD的最优参数解析解[3]。考虑主结构阻尼时，TMD最优参数的解析解很难求解，Sadek则通过数值方法求解了有阻尼体系TMD的最优参数[4]。Rana对TMD参数的研究结果表明使用简谐激励理论设计的TMD能有效控制结构的地震响应[5]。我国学者李春祥采用数值迭代法给出了地震作用下的TMD最优参数实用设计表格[6]。李创第等人基于结构动力可靠性约束对TMD进行了优化设计[7]。谭平等人采用虚拟激励法从能量角度分析了主结构能量响应最小时TMD质量比、频率比以及阻尼比的最优值[8]。

目前，大多数TMD设计均是将结构简化为不考虑弯曲变形的多质点剪切模型。但是，框剪结构的弯曲变形一般情况下是不可忽略的。鉴于此，本文将结构简化为连续-离散的动力模型，该模型不但能体现结构的剪切变形，而且能充分考虑结构弯曲变形产生的弯曲转角对TMD动力特性的影响。使用Rayleigh-Ritz法分析了结构动力特性，在此基础上，基于结构性能目标使用遗传算法对TMD进行数值优化设计。最后，针对某框剪结构TMD减震体系的优化设计问题进行了研究，研究结果验证了本文方法的有效性。

1 框剪结构的连续-离散动力模型

框剪结构的连续-离散动力模型如图1所示。假定弯曲型构件只考虑弯曲变形，剪切型构件只考虑剪切变形。图中m¯i、EiIi以及li分别表示第i层的线性分布质量、弯曲型构件等效抗弯刚度与层高。ki表示第i层剪切型构件剪切刚度，mi表示第i层的楼层质量，n表示结构层数。

由于集中参数对悬臂梁边界条件影响较大，导致其理论推导较为繁琐复杂。本文采用Rayleigh-Ritz法对结构进行自振特性分析。Rayleigh-Ritz法是一种缩减系统自由度的近似方法，将振型函数用一组相互独立且满足部分或全部几何物理边界条件的函数φj（x）的线性组合来表示：

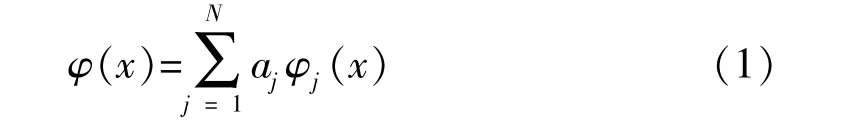
根据文献 [9]，研究结构振型时，令位移

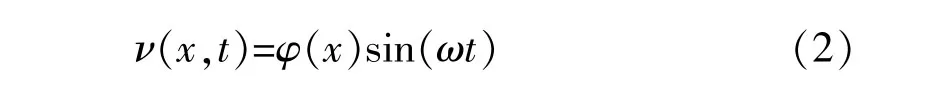
则结构最大动能与势能

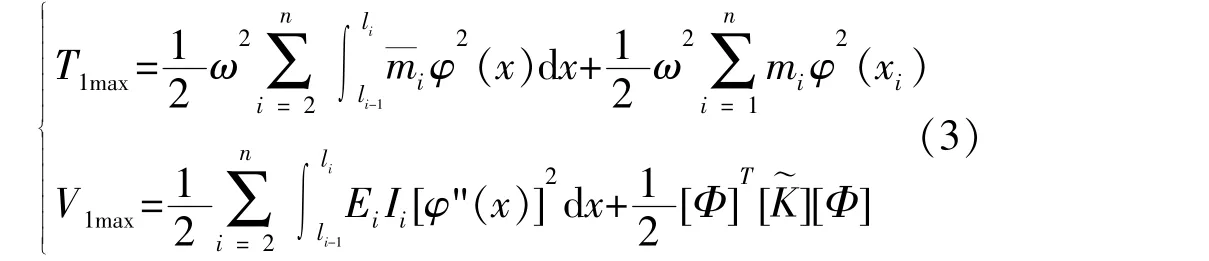
式（3）中， “″” 表示对x的二阶偏导，

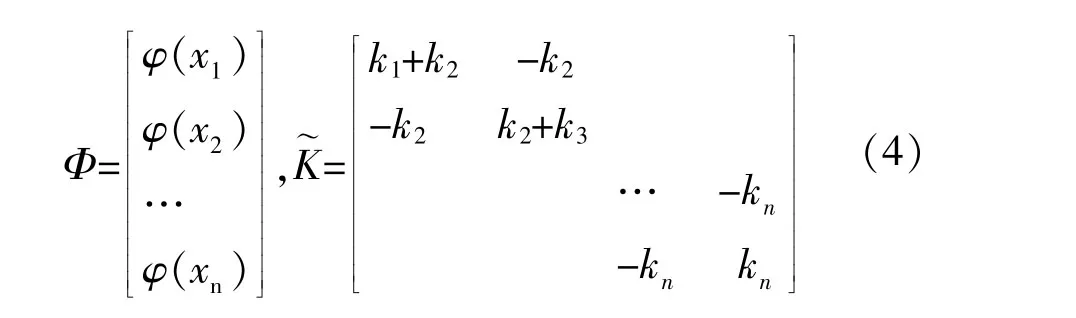
设结构能量泛函L1=T1max-V1max，由能量守恒定律得

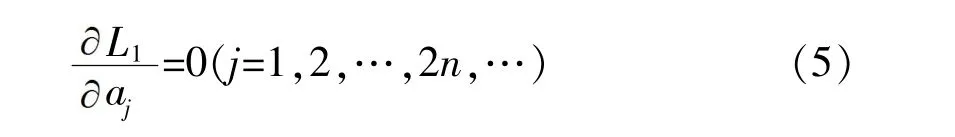
联立（1）～（5）式，可得出结构自振周期与振型函数。

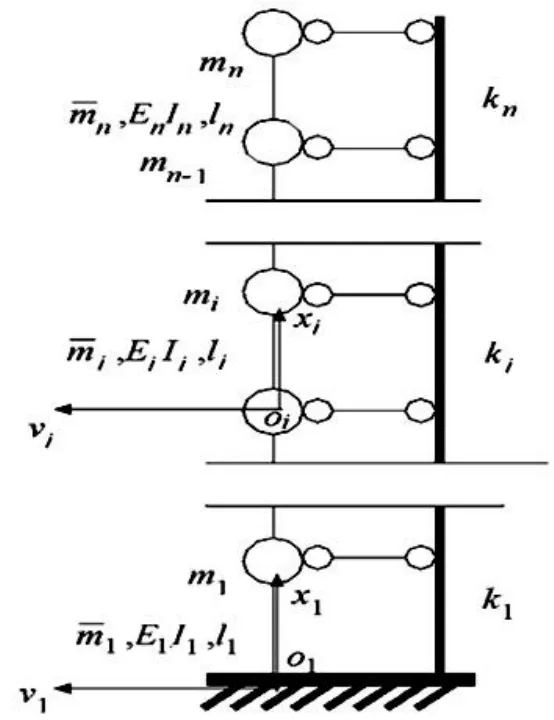
图1 连续-离散动力模型Fig.1 Bending shear structure dynamic model

2 TMD体系运动方程

不失一般性，假定TMD安装于结构第i层用于控制结构第r阶振型位移。以结构xi处φr（x）为基准将振型函数进行归一化处理。假定结构以单一形式φr（x）振动，则认为结构可简化为广义单自由度模型[10-12]。 令结构参数可表示为：

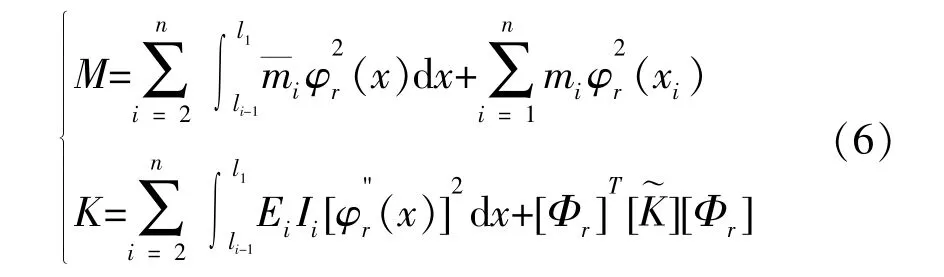
设结构位移 ν（x，t）=φr（x）z1（t）， 其中，z1（t）表示结构xi处相对于地面的位移。结构-TMD无阻尼体系数学模型如图2所示，图中，Ks与Kb分别表示结构弯曲刚度与剪切刚度，mt和kt表示TMD的质量与刚度系数，z2表示TMD相对于结构的位移，θ（t）表示结构 xi处的弯曲转角。 假定 θ（t）=β（xi）z1（t），其中 β（xi）表示结构 xi处的转角系数， 本文 β（xi）=设结构-TMD无阻尼体系的总动能为T，总势能为V，有（以系统初始位置为零势能点）

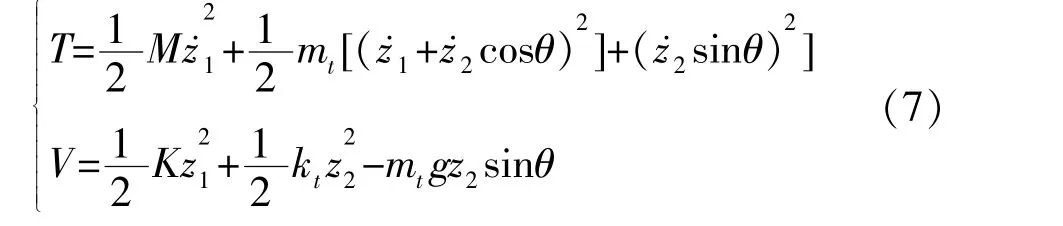
式（7）中， “·”表示对时间求导。设Lagrange函数

将 θ=βz1带入（6）与（7）式化简得

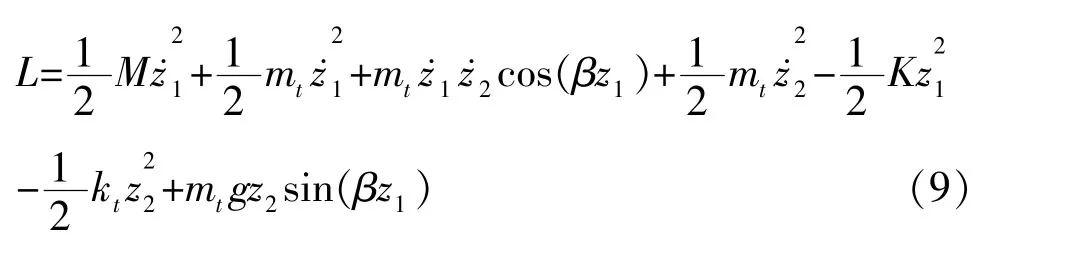
代入Lagrange方程

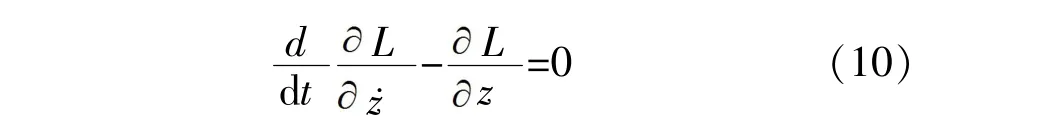
求得结构-TMD无阻尼体系自由振动方程为

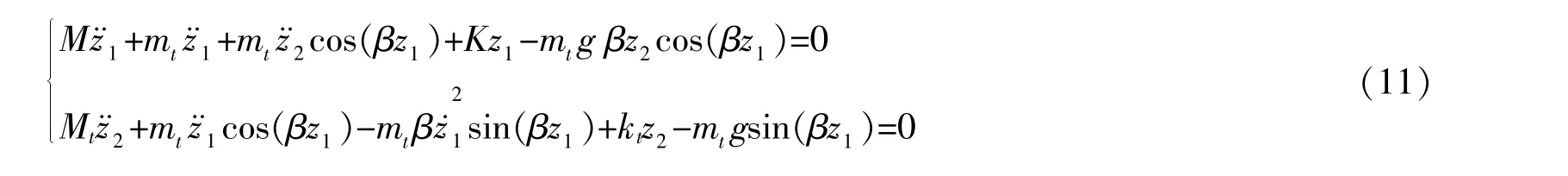
假定结构r阶振型阻尼比为ζ1以及TMD阻尼比为ζ2，则结构阻尼系数可表示为C=2ζ1ωrM，TMD阻尼系数ct=2ζ2ωtmt。 其中， ωr表示结构第r阶振型对应振动频率，ωt表示TMD振动频率。则TMD频率比可表示为f=ωt/ωr。同样可由Lagrange方程求得地震作用下结构-TMD有阻尼体系运动方程为：

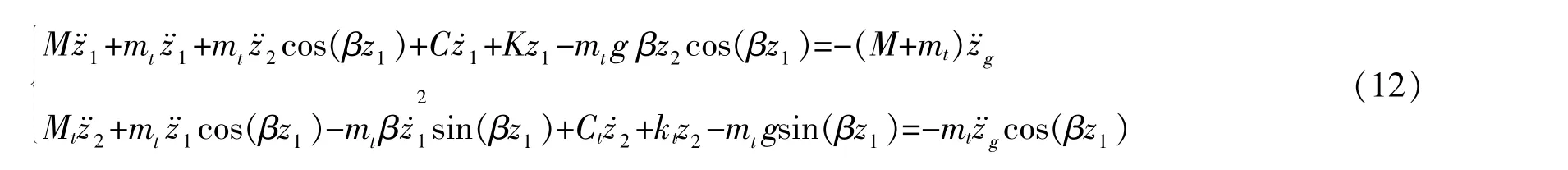
同理，不考虑结构弯曲转角，即β=0时，结构-TMD体系运动方程为：

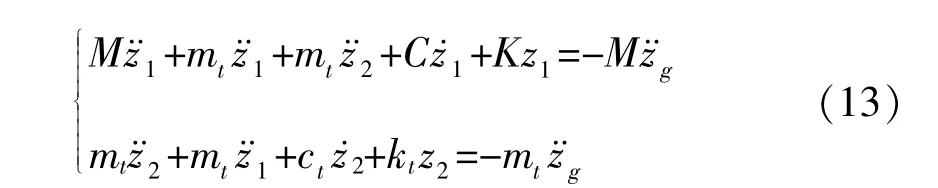
3 基于结构性能目标的TMD优化设计流程

本文以位移作为结构性能评价指标，提出基于结构性能目标的TMD优化设计流程如下：

（1）建立位移反应谱。由地震加速度时程建立结构设计位移反应谱。

（2）根据地震设防水准、结构的重要性等因素确定结构广义单自由度目标位移νd。

（3）计算设计水平地震力。广义单自由度的目标位移确定后,广义单自由度的设计水平地震力fd=Kνd。

（4）以广义单自由度的设计水平地震力作为外激励幅值，假定外激励为结构第r阶振型频率对应的简谐激励fdeiwrt，运用遗传算法对TMD进行数值优化设计。

4 基于遗传算法的TMD最优参数求解

由于式（10）与式（11）理论求解比较复杂，本文基于MATLAB平台使用Runge-Kutta法对其进行数值求解，采用遗传算法对TMD进行数值优化设计。遗传算法（Genetic Algorithm，简称GA）是一类借鉴生物界的进化规律演化而来的优化搜索方法，算法详细介绍见文献 [13]

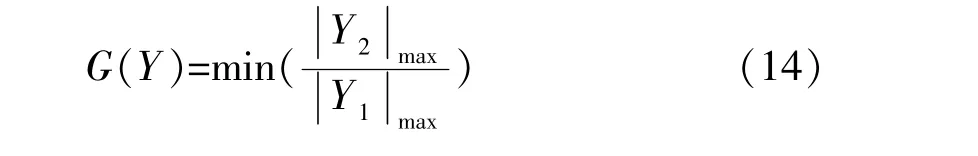
以结构层间位移角限值[σ]作为约束条件，即

5 算例

5.1 工程概况

为了验证本文方法的有效性，以某20层现浇钢筋混凝土框剪结构作为算例。建筑层高3 m，总高度60 m。结构平面布置：横向5×4 m，纵向5×4 m，结构总质量1.06×104t。结构每层分布质量m¯取1.08×105kg/m， 集中质量m=2.06×105kg。 每层剪力墙等效抗弯刚度EI=1.13×1011N·m2，框架剪切刚度 K=3.13×109N/m。结构顶层转角系数β=4.75×10-3。假定TMD安装于结构顶层，用于控制结构横向第一阶振型，结构第一阶振型阻尼比ζ1=0.05。采用Etabs软件建模如图3所示。用Etabs软件计算该结构基本周期为1.03 s，用Rayleigh-Ritz法求得的简化模型基本周期为0.99 s，二者误差为3.89%，说明本文简化模型满足精度要求。

图3 算例模型图Fig.3 Diagram of simulation example

本文根据工程实际情况选取人工地震波以及ELcentro波作为地震输入，以此来评判TMD控制效果。其中，人工地震波加速度谱密度采用Kanai-Tajimi谱[15-16]：

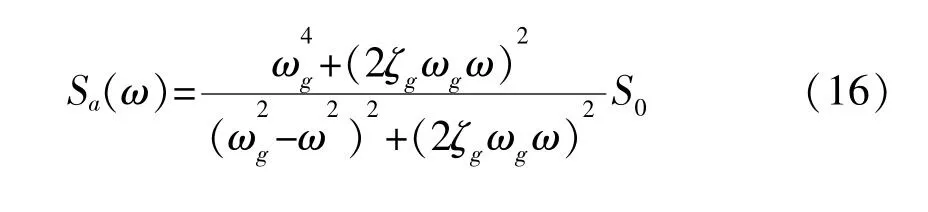
式（16）中， S0表示谱强度因子， ζg和 ωg分别表示地基土的阻尼比与卓越频率。时间包络函数取为：

式（17）中，c为衰减系数，T1与T2分别表示主振平稳段开始与结束时间。

现考虑地震设防烈度为8度，C类场地，设计地震分组为第一组，由文献[17]取，ωg=17.95rad/s，ζg=0.72， S0=14.56 cm2/（rad.s3）， T1=0.8 s， T2=7.0 s，c=0.35，按照三角级数法生成的地震加速度时程曲线如图4所示。由人工波生成的结构位移反应谱如图5所示，由图5易见，本文模型的目标位移νd=0.01 m。

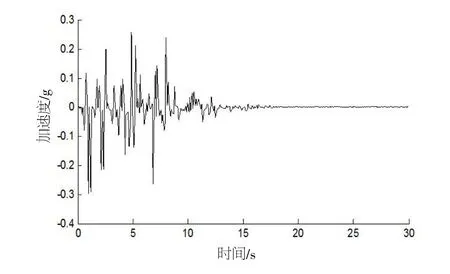
图4 人工地震波Fig.4 Artificial seismic wave

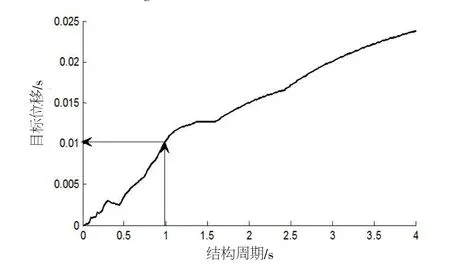
图5 结构位移反应谱Fig.5 The response spectrum of structural displacement

5.2 TMD谐波响应分析

在求解TMD最优参数前，首先验证考虑结构弯曲转角的必要性。假定结构阻尼比为0，使用Den Hartog参数对TMD进行设计。以结构顶点位移响应峰值作为评价指标，计算出谐波fdeiwrt作用下，结构转角系数与结构位移响应之间的关系如图6所示。从图6中可以看出，随着转角系数β值的不断增大，TMD对结构位移响应峰值的控制存在相对较为稳定的 “平台段”以及变化剧烈的“振荡段”。本文算例的转角系数位于 “振荡段”[0.004，0.005]内，在此区间并非TMD质量比越大，其控制效果就越好。因此，本文建议将TMD质量比作为遗传算法优化参数之一。

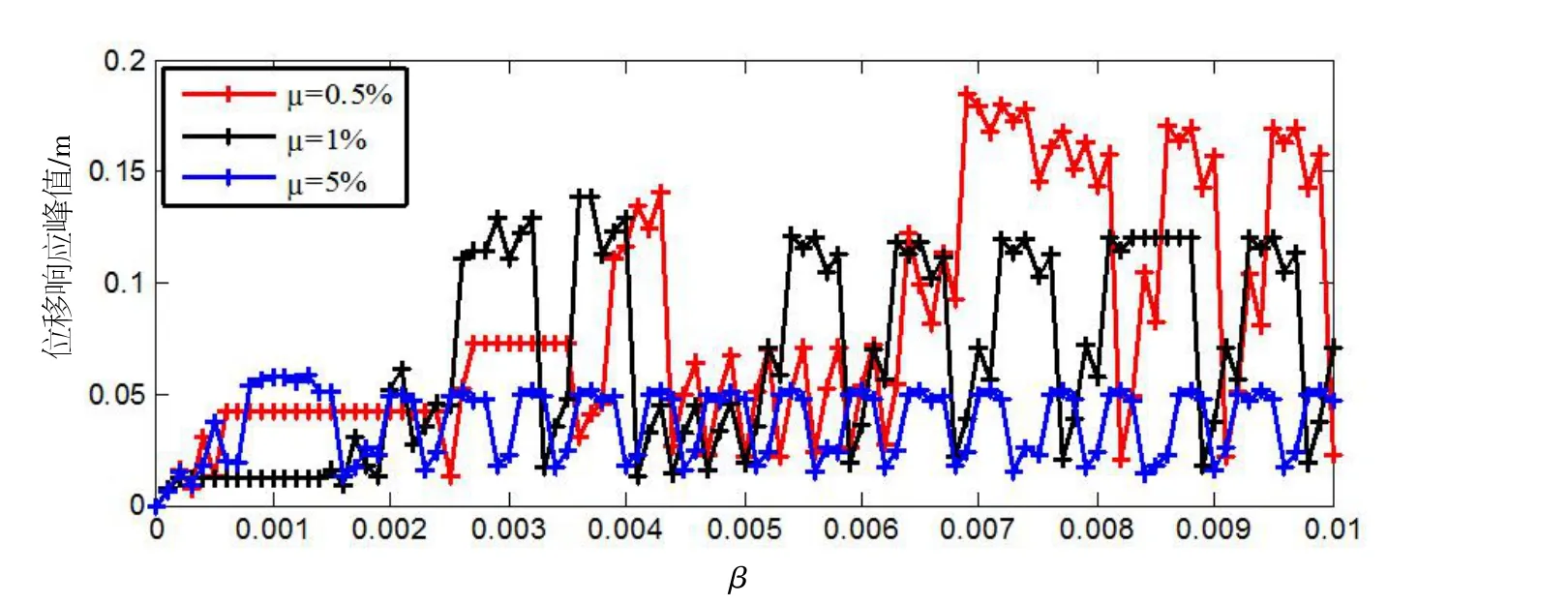
图6 结构顶点位移响应峰值与结构转角系数关系曲线Fig.6 The relationship between the peak value of the top displacement response and bending angle coefficient

5.3 TMD最优参数求解

使用遗传算法对TMD最优设计参数进行求解，其中，TMD阻尼比与频率比分别取为 [00.2]与 [0.81.2]，TMD质量比取 [00.05]。遗传算法中各参数分别取为：种群大小80，遗传60代，交叉概率0.7，变异概率0.1。根据我国 《框剪建筑混凝土结构技术规程》（JGJ 3-2010）[14]取 Δνmax/l≤1/800。求解出TMD最优频率比fopt=0.869与最优阻尼比ζ2opt=0.0901，与之对应的TMD最优质量比μ=0.045。

为了便于分析，假定本文方法所设计的TMD为TMD1，使用Den Hartog参数设计的TMD为TMD2， TMD2的质量比取为0.09。图7表示地震作用下结构的位移响应时程，相对于TMD2而言，TMD1处于更好的控制状态。以人工波作用下的结构位移响应均方差为例，结构无控状态下的位移响应均方差为2.1×10-3m，TMD2控制下结构位移响应均方差为1.8×10-3m，控制效果为14.29%。TMD1控制下结构位移响应均方差为1.4×10-3m，控制效果为33.33%，较TMD2提高了19.04%。值得注意的是，TMD1的质量比相对于TMD2减小了50%，控制效果反而比TMD2好。这也说明了本文将TMD质量比作为优化参数的正确性，同时也验证了本文所提方法的有效性。

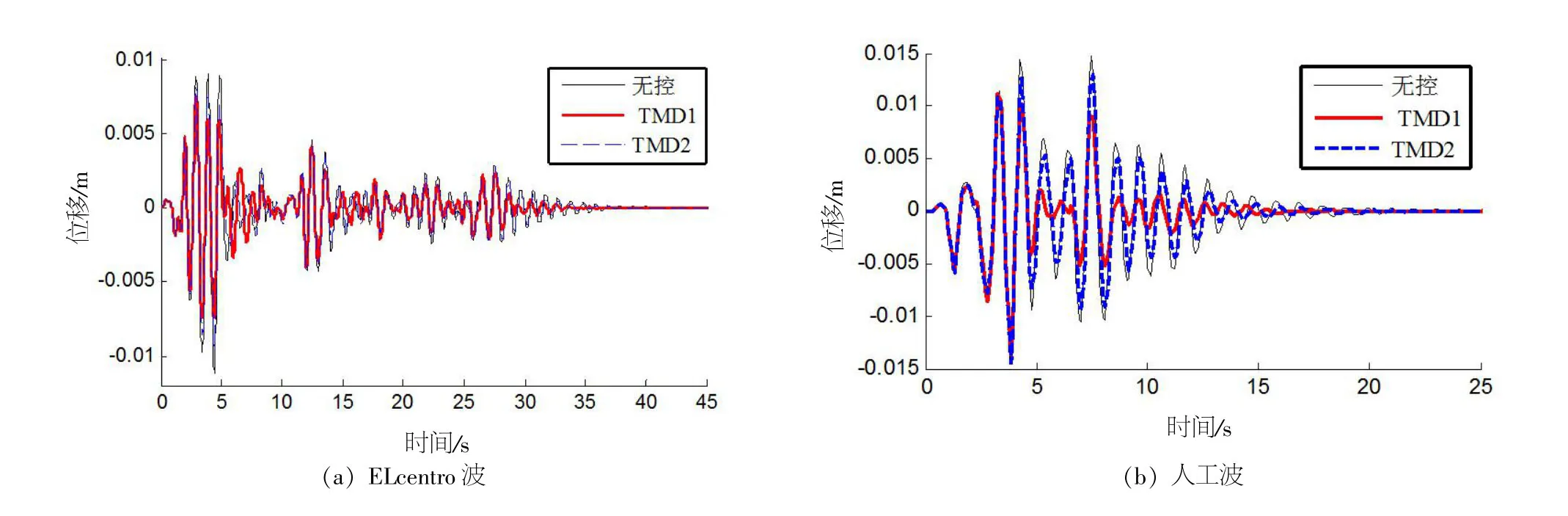
图7 地震作用下结构的位移响应时程Fig.7 The time history of structural displacement response under earthquake

6 结语

本文提出了一种适用于框剪结构的TMD减震体系优化设计方法，该方法考虑框剪结构弯曲变形产生的转角对TMD动力特性的影响，使用Rayleigh-Ritz法分析了结构动力特性，在此基础上，基于结构的性能目标使用遗传算法对TMD体系进行数值优化设计。以1栋20层框剪结构-TMD减震系统优化设计作为算例，验证了本文方法的有效性。得到以下结论：

（1）基于结构性能目标结合遗传算法提出了一种适用于框剪结构的TMD减震体系数值优化设计方法，该方法充分考虑结构弯曲变形产生的转角对TMD动力特性的影响。

（2）考虑结构弯曲转角时，TMD质量比越大其控制效果不一定越好。因此，本文建议将TMD质量比也作为TMD优化设计参数之一。

（3）对于本文算例，使用本文方法设计的TMD1比传统参数设计的TMD2质量更小且控制效果更好。其中，TMD2质量比为0.09，TMD1质量比为0.045，较TMD2减小了50%。但是，TMD1的控制效果较TMD2提高了19.04%。

[1]周福霖.工程结构减震控制[M].北京：地震出版社，1997.

[2]王肇民.高耸结构振动控制[M].上海：同济大学出版社，1997.

[3]Den Hartog J P.Mechanical Vibration[M].NY：McGraw Hill，1956.

[4] Sadek F.M， Ohraz B.T， Aylor A.W.A method of estimating the parameters of tuned mass dampers for seismic applications[J].Earthquake Engineering and Structural Dynamics， 1997， 26 （6）： 617-635.

[5]Rana R，Soog T.T.Parametic study and simplified design oftuned mass damper[J].Engineering Structures，1998， 20： 193-204.

[6]李春祥.地震作用下框剪建筑TMD控制研究与设计[J].上海交通大学学报，1999，33（6）：746-749.

[7]李创第，黄天立，李暾，等.带TMD的结构基于动力可靠性约束的优化设计[J].地震工程与工程振动，2004， 24 （6）： 121-125.

[8]谭 平，潘兆东，王磊，等.基于能量原理的TMD系统减震性能分析[J].桂林理工大学学报，2012，32（3）：335-341.

[9]王光远.应用分析动力学[M].北京：人民教育出版社，1981.

[10]R.克拉夫，J.彭津，王光远，等.结构动力学[M].北京：高等教育出版社，2006.

[11]刘晶波，杜修力.结构动力学[M].北京：机械工业出版社，2005.

[12]梁兴文.结构抗震性能设计理论与方法[M].北京：科学出版社，2011.

[13]王 磊，谭 平，赵卿卿.随机结构-TMD优化设计与概率密度演化研究[J].振动工程学报，2015，28（2）：285-290.

[14]广东省建筑设计研究院.JGJ 3-2010框剪建筑混凝土结构技术规程[S].北京:中国建筑工业出版社，2011.

[15]朱位秋.随机振动[M].北京：科学出版社，1992.

[16]杨庆山，田玉基.地震地面运动及其人工合成[M].北京：科学出版社，2014.

[17]薛素铎，王雪生，曹资.基于新抗震规范的地震动随机模型参数研究[J].土木工程学报，2003,36（5）：5-10.

Optimization Design of Frame ShearStructure-TMD System

HE Hui1， TAN Ping1， LIU Liangkun2

（1.Earthquake Engineering Research&TestCenter， Guangzhou University， Guangzhou 510405， China；2.School of Civil Engineering，Beijing University of Technology，Beijing 100124， China）

This paper proposes a simple and practical numerical optimization design method for frame shear structure-TMD system.Frame shear structure is simplified into a continuous cantilever beam with lumped parameter model.This model can not only simulate the structural lateral displacement reasonably,but also consider structural bending deformation.Structural natural vibration characteristics were analyzed by using Rayleigh-Ritz method.Optimal design of TMD based on the genetic algorithm,with the structural performance asoptimization objective.The methods applied to the optimum design of a frame shear structure-TMD damping system to reduce seismological response,and its numeral simulation analysis was conducted.The analysis results indicate this TMD numerical optimization method is very effective.

Frame shear structure； TMD； Rayleigh-Ritz method； Story drift； Genetic Algorithm

TU311.3

A

1001-8662（2017）02-0100-06

10.13512/j.hndz.2017.02.016

贺 辉，谭 平，刘良坤.考虑弯曲转角的框剪结构-TMD减震体系数值优化设计[J].华南地震，2017，37（2）：100-105.[HE Hui，TAN Ping，LIULiangkun.OptimizationDesign ofFrame ShearStructure-TMD System[J].South china journal of seismology，2017，37（2）：100-105.]

2017-03-23

教育部创新团队研究发展计划（IRT13057）、国家自然科学基金（51208129；51478129）、广州市属高校 “羊城学者”首席科学家培养项目（1201541630）、 “广东特支计划”科技创新领军人才（2014TX01C141）

贺 辉 （1992-），男，硕士研究生，主要从事结构振动控制研究。

E-mail：937675375@qq.com.

谭 平 （1973-），男，博士，研究员，博导，主要从事结构抗震与减震控制研究。

E-mail:ptan@gzhu.edu.cn.