WGS-84模型下时差频差半定规划定位算法

李万春*,彭吴可,彭丽,马叶子,李英祥

1.电子科技大学 电子工程学院 网络空间安全研究中心,成都 611731

2.成都信息工程大学 通信工程学院 气象信息与信号处理四川省高校重点实验室,成都 610225

3.清华大学医学院,北京 100084

WGS-84模型下时差频差半定规划定位算法

李万春1,2,*,彭吴可1,3,彭丽1,马叶子1,李英祥2

1.电子科技大学 电子工程学院 网络空间安全研究中心,成都 611731

2.成都信息工程大学 通信工程学院 气象信息与信号处理四川省高校重点实验室,成都 610225

3.清华大学医学院,北京 100084

利用多颗卫星的时差频差对辐射源进行位置和速度的测量,其本质意义上是一个含有噪声项的高度非线性方程组求解问题,针对地面目标而言,可以采用基于WGS-84地球模型作为目标位置和速度约束,更进一步的增加了定位系统的复杂性。提出了一种基于半定规划(SDP)的定位解算法,将非线性方程求解问题通过适当的松弛,转化为半定优化(SDO)的问题,借助于业界较为成熟的CVX等优化软件进行定位求解,并研究了该模型条件下的克拉美罗下界(CRLB)。仿真结果表明,该算法能够较好地逼近克拉美罗下界。

WGS-84模型;时差定位;频差定位;半定规划;克拉美罗下界

空间中相距一定距离的多颗卫星组成卫星簇,测量地面辐射源辐射的电磁信号传播到其中两颗卫星的到达时间差,以及信号到达两卫星的频率差,结合辐射源所在地球面作为定位面,就可以实现辐射源定位[1-3]。

基于时差频差测量的辐射源定位问题,相关文献最早见于Ho和Xu提出的两步加权最小二乘(2WLS)解析算法[1],其核心思想是在待求目标位置与速度未知的情况下引入参考站到目标的斜距和斜距变化率,通过一定的代数转换将复杂的非线性测量方程转化为针对上述未知量的线性方程,采用加权最小二乘法(WLS)获得未知量的初始解,再根据斜距与斜距变化率与目标位置速度之间的约束关系,利用WLS得到最终的定位解。在文献[4]的基础上,文献[5]引入了观测器误差,获得了更为稳健的定位解。文献[6]引入了多维标量的方式进行目标定位。文献[7-11]从不同的角度讨论了到达时差(TDOA)联合到达频差(FDOA)定位问题。

将半定规划(SDP)引入到定位领域是当下较为热门的问题[12-16],Wang等[17]给出了一种基于SDP的TDOA与FDOA联合定位算法,通过一定的转换与松弛,将非线性测量方程转化为SDP问题再求解。文献[18-20]讨论了几种集中式的TDOA与FDOA联合定位算法。

对于利用已知目标的地理海拔高度进行TDOA与FDOA的联合定位问题,文献[21]给出了一种解析算法,该算法通过非线性测量方程,将问题转化为求解一元高阶多项式方程。由于该方法没有考虑到测量方程的误差影响,所以在测量噪声较大的情况下不够稳健。本文在文献[17]的基础上,结合 WGS-84模型,并将该模型作为约束条件,提出了一种基于半定规划的稳健定位求解算法,仿真结果表明,该算法收敛较快,精度高,算法的稳健性好,是一种有效的定位算法。论文章节安排如下:第1节为定位模型,第2节为定位算法,第3节为仿真分析,第4节为结论。

1 定位模型

假设某时刻在地固坐标系(ECEF)中,空间中N颗卫星的位置和速度分别为si(i=1,2,…,N)和˙si(i=1,2,…,N),分别接收地面上某一辐射源发射的同一脉冲信号,比较脉冲到达时间,得到N-1组独立的TDOA,比较脉冲到达频率(FOA),得到N-1组独立的FDOA。在三维空间中,根据每一组独立的时差测量和每一组独立的频差测量都可以分别得到一个单叶双曲定位面,两个双曲面和地球面的交点就是目标所在的位置。

假设该时刻卫星和目标的大地直角坐标分别为si(i=1,2,…,N)、˙si(i=1,2,…,N)和u、˙u。若测得的时差、频差为τi1、fi1,那么可得到测量方程为

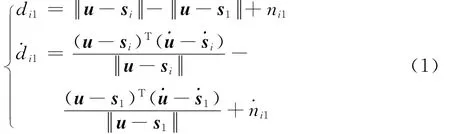
式中:i=2,3,…,N,di1=cτi1,˙di1=cfi1,c为电磁波的传播速率。

本算法以地球面作为定位面,对其进行精确建模。通常使用的地球面都是正球面模型,该模型和真实地球面相去甚远,所以采用和地球面密合较好的WGS-84地球椭球面模型。

在WGS-84坐标系下,具有高程的目标的直角坐标和大地经纬高坐标的关系为

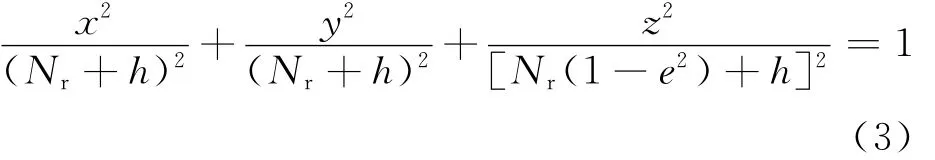
将式(3)两端对时间求导,可得

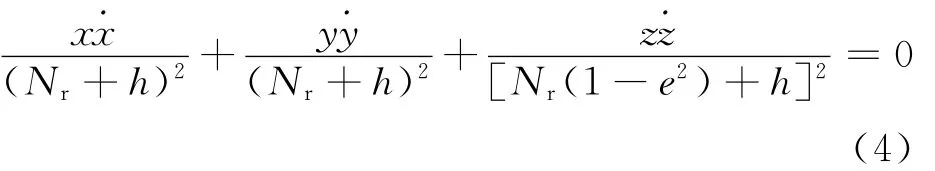
将式(1)、式(3)和式(4)所构成的复杂非线性方程组联立求解,即可求出目标的大地坐标向量[x y z]和速度向量[˙x ˙y ˙z]。

式(3)和式(4)可以分别简记为

2 定位算法

2.1 基于TDOA和FDOA测量的目标定位

将时差和频差的测量噪声写作Δα=[nT˙nT],其 中n=[n21n31… ni1]T,˙n=[˙n21˙n31… ˙ni1]T。ni1、˙ni1分别为第i站和第1站之间的时差、频差测量误差。假设Δα～N(0,Qα),其中Qα为噪声的协方差。将时差、频差以及观察站和辐射源的距离差、速度差的值定义为

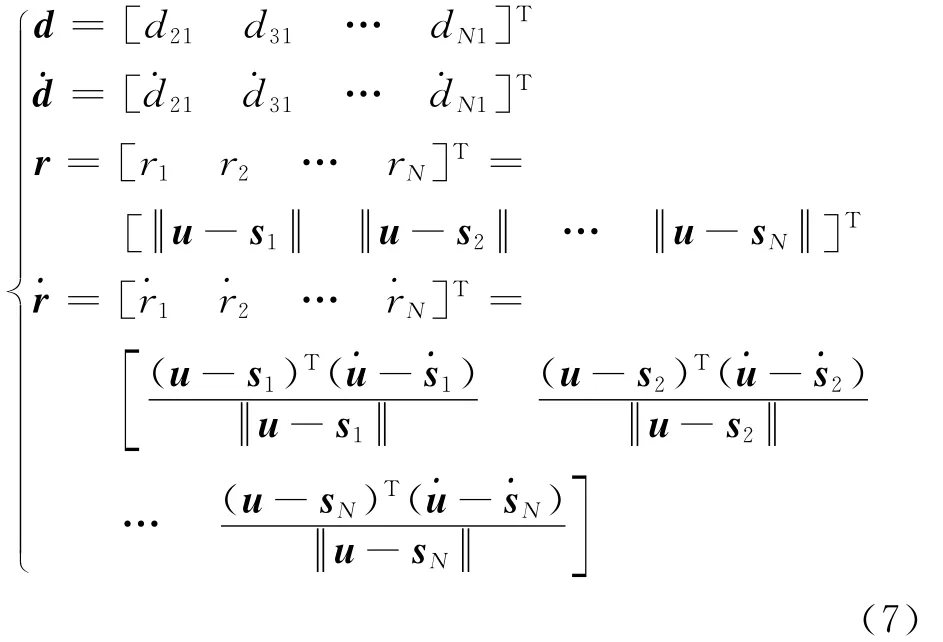
整理后可得

式中:G=[-1N-1IN-1]。-1N-1为N-1行1列的全1向量,将两式合并可得

由最大似然估计可知,待估计的参数应该使已测量到的数据出现的概率尽可能的大,因此建立目标函数为

2.2 目标定位的加权最小二乘解

将以上最大似然估计转化为加权最小二乘估计,详细的证明过程见文献[1]。

式中:

其中:B1=2diag(r2,r3,…,rN);˙B1=2diag(˙r2,˙r3,… ,˙rN)。

要利用该方法求解需要假设初值^φ=[^uT^u·T]T。根据初值估计出加权矩阵^Q=^BQα^BT。在本文的计算中直接假设初值^φ=0,计算出结果后进行一次迭代计算。

2.3 利用SDR方法得到WGS-84模型下的SDP形式

首先对目标函数进行转化:

由中间变量r1,˙r1的物理意义可以得到约束条件为

根据式(13)由柯西许瓦兹不等式可得到

将Y=yyT代入可变换为

由WGS-84模型约束等式(3)和式(4),可得到约束条件为

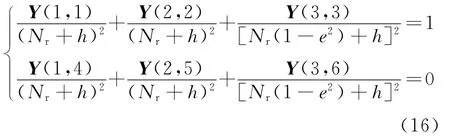
将式(16)代入SDP问题中可得到

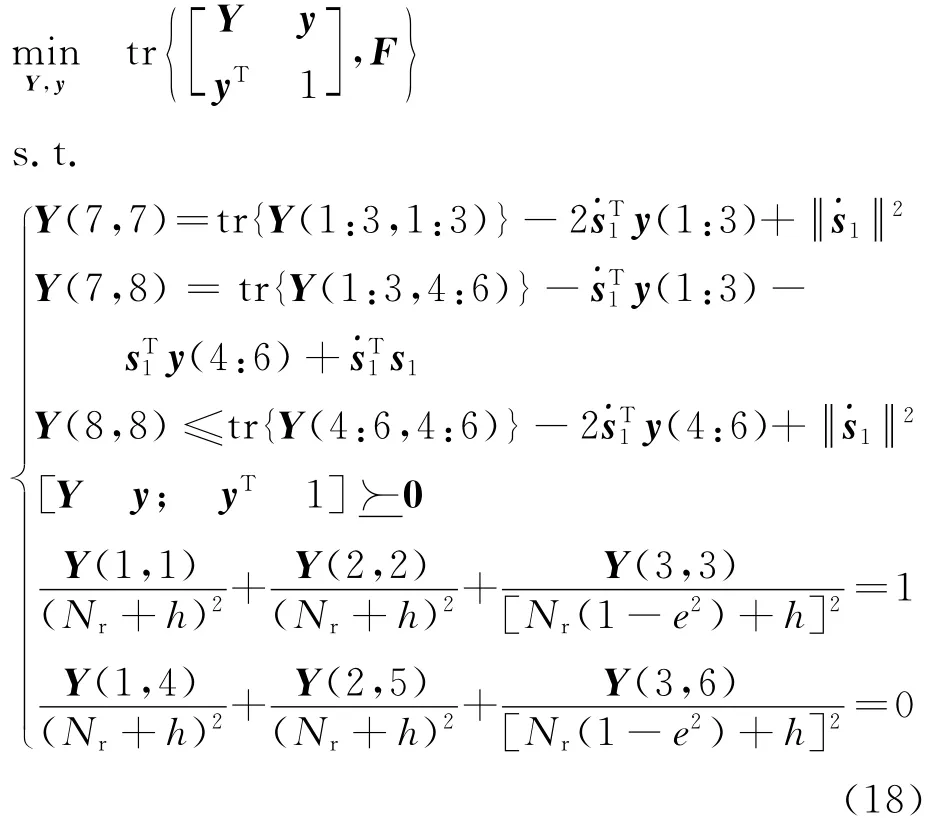
据此,对于标准的半定规划问题,可利用相关的凸优化工具来求解。

如果目标静止的话,推导如上,只需要将y中的第4～6行的元素置零即可。最后得到静止目标定位求解的SDP为

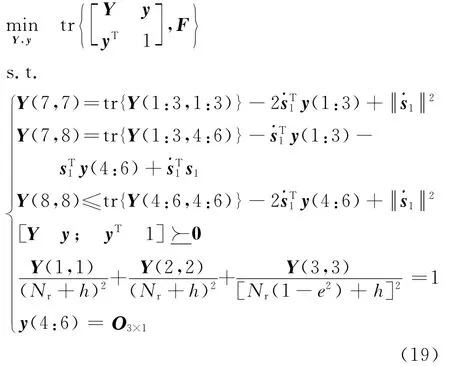
3 仿真分析

本节中考察目标静止与运动2种情况下的定位仿真。

1)静止目标的定位

采用5个卫星观察站进行定位,卫星观察站的位置与速度(ECEF坐标)如表1所示。

假设目标位置为u=[-1 961 3 395 5 020]km,设定WGS-84模型的参数分别为:长半径a=6 378.137 km,偏心率e=0.003 352 810 664,h=0 km。该仿真主要针对于海平面上的目标,因此将问题简化为目标高程差为零来计算。仿真结果如图1所示。

表1 观察站的位置和速度Table 1 Location and velocity of observatories

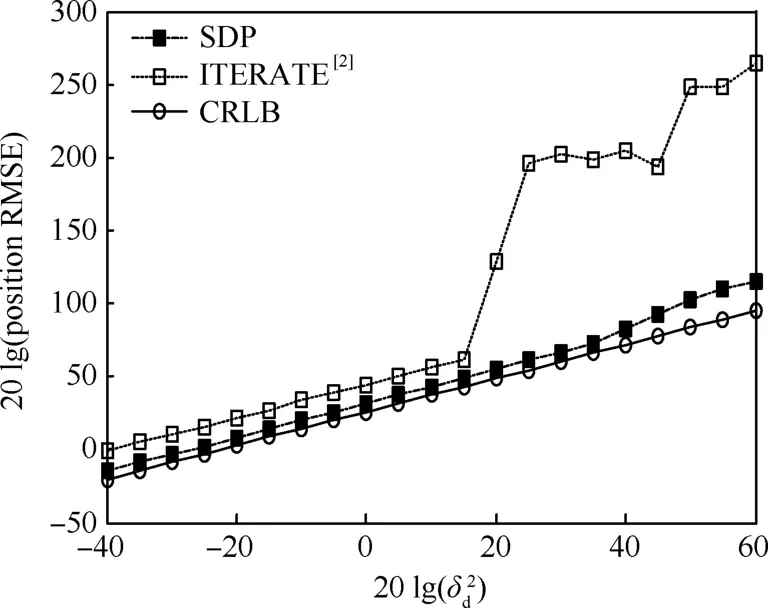
图1 静止目标不同定位方法的位置RMSE比较Fig.1 Comparison of location RMSE with different positioning methods for stationary target

2)运动目标的定位

设定目标位置为u=[-1 961 3 395 5 020]km,速度为˙u=[-6.5 -10 -18]km/h。假设WGS-84模型的参数分别为:长半径a=6 378.137 km,偏心率e=0.003 352 810 664,h=0 km。该仿真同样是针对于海平面上的目标,因此将问题简化为目标高程差为零来计算。仿真结果如图2所示。

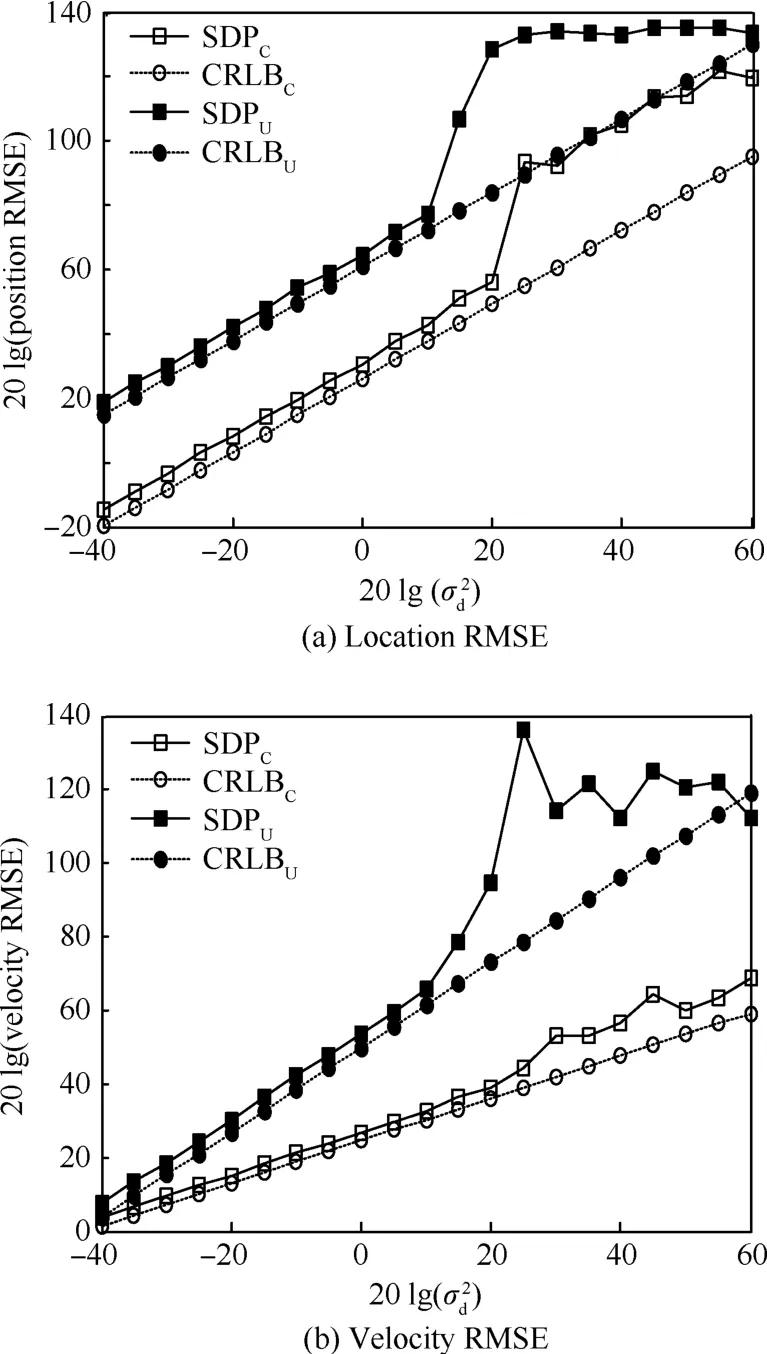
图2 运动目标不同定位算法的位置和位置和速度RMSE比较Fig.2 Comparison of location and velocity RMSE with different positioning algorithms for moving target

仿真图绘制了带约束条件的SDP算法(SDPC)和不带约束条件的SDP算法(SDPU)的仿真结果,同时还绘制了其分别的CRLB限。从理论分析和仿真结果图2(a)与图2(b)中可以得到,引入WGS-84模型约束后,定位的理论精度对比于无约束时有较大的提升,并且该定位算法的性能接近克拉美罗下界。

4 结 论

1)本文提出了一种在WGS-84模型下的时差频差联合SDP定位算法。

2)在测量噪声适当的情况下,所提方法性能逼近CRLB。

3)相比解析算法[4],本文算法更具备稳健性。

[1] HO K C,XU W.An accurate algebraic solution for moving source location using TDOA and FDOA measurements[J].IEEE Transactions on Signal Processing,2004,52(9):2453-2463.

[2] HO K C,CHAN Y T.Geolocation of a known altitude object from TDOA and FDOA measurements[J].IEEE Transactions on Aerospace&Electronic Systems,1997,33(3):770-783.

[3] 叶尚福,孙正波,夏畅雄.卫星干扰源双星定位技术及工程应用[M].北京:国防工业出版社,2013:61-99.

YE S F,SUN Z B,XIA C X.Satellite interference location technology and engineering application[M].Beijing:National Defense Industry Press,2013:61-99(in Chinese).

[4] HO K C,LU X,KOVAVISARUCH L.Source localization using TDOA and FDOA measurements in the presence of receiver location errors:Analysis and solution[J].IEEE Transactions on Signal Processing,2007,55(2):684-696.

[5] SUN M,HO K C.An asymptotically efficient estimator for TDOA and FDOA positioning of multiple disjoint sources in the presence of sensor location uncertainties[J].IEEE Transactions on Signal Processing,2011,59(7):3434-3440.

[6] WEI H W,PENG R,WAN Q,et al.Multidimensional scaling analysis for passive moving target localization with TDOA and FDOA measurements[J].IEEE Transactions on Signal Processing,2010,58(3):1677-1688.

[7] YANG K,JIANG L,LUO Z Q.Efficient semidefinite relaxation for robust geolocation of unknown emitter by a satellite cluster using TDOA and FDOA measurements[C]//IEEE International Conference on Acoustics,Speech and Signal Processing,2011:2584-2587.

[8] KIM Y H,HAN J W,SONG K H,et al.Emitter location based on the linearization of quadratic TDOA and FDOA curves[C]//International Conference on Electronics,Information and Communications,2014:1-2.

[9] QUO F,HO K C.A quadratic constraint solution method for TDOA and FDOA localization[C]//IEEE International Conference on Acoustics,Speech and Signal Processing,2011:2588-2591.

[10] ICKI D,KAUNE R,KOCH W.Mobile emitter geolocation and tracking using TDOA and FDOA measurements[J].IEEE Transactions on Signal Processing,2010,58(3):1863-1874.

[11] VAGHEFI R M,BUEHRER R M.On the CRLB of TDOA/FDOA estimation from MIMO signals[C]//IEEE/ION Position,Location and Navigation Symposium-PLANS,2016:772-778.

[12] TAKABAYASHI Y,MATSUZAKI T,KAMEDA H,et al.Target tracking using TDOA/FDOA measurements in the distributed sensor network[C]//IEEE Xplore Sice Conference,2008:3441-3446.

[13] ZHANG W,ZHANG G,HU J.Rrsearch on priori information of TDOA/FDOA in satellite communication based on ephemeris of satellite[C]//IEEE International Conference on Signal Processing,Communications and Computing,2011:1-4.

[14] YANG K,WANG G,LUO Z Q.Efficient convex relaxation methods for robust target localization by a sensor network using time differences of arrivals[J].IEEE Transactions on Signal Processing,2009,57(7):2775-2784.

[15] BISWAS P,LIAN T C,WANG T C,et al.Semidefinite programming based algorithms for sensor network localization[J].ACM Transactions on Sensor Networks,2006,2(2):188-220.

[16] WANG G.A semidefinite relaxation method for energybased source localization in sensor networks[J].IEEE Transactions on Vehicular Technology,2011,60(5):2293-2301.

[17] WANG G,LI Y,ANSARI N.A semidefinite relaxation method for source localization using TDOA and FDOA measurements[J].IEEE Transactions on Vehicular Technology,2013,62(2):853-862.

[18] DU Y,WEI P.An explicit solution for target localization in noncoherent distributed MIMO radar systems[J].IEEE Signal Processing Letters,2014,21(9):1093-1097.

[19] YANG H,CHUN J.An improved algebraic solution for moving target localization in noncoherent MIMO radar systems[J].IEEE Transactions on Signal Processing,2016,64(1):258-270.

[20] LIANG J,LEUNG C S,SO H C.Lagrange programming neural network approach for target localization in distributed MIMO radar[J].IEEE Transactions on Signal Processing,2016,64(6):1574-1585.

[21] STOICA P,NG B C.On the Cramer-Rao bound under parametric constraints[J].IEEE Signal Processing Letters,1998,5(7):177-179.

附录A

克拉美罗下界(CRLB)是一个无偏线性估计量能达到的最低方差,其值为Fisher矩阵的逆,Fisher矩阵定义为

式 中:q=[r21r31… rN1˙r21˙r31…˙rN1]T;ri1和˙ri1为没有误差的di1和˙di1即第i站和第1站之间真实的时差和频差值;p(q;θ)为q的概率密度函数,θ为待估计的参数。对于本文的算法,需要考虑两种情况,一是静止目标,二是运动目标。首先考察静止目标。

1)静止目标无约束CRLB

式中:qo(θ)为服从高斯分布的概率密度函数p(q;θ)的均值;Q为其协方差矩阵。

由文献[17]可得

2)静止目标约束CRLB

由文献[21]可知,当存在额外的约束条件时其CRLB为

式中:F为约束条件关于估计量的梯度,即

其CRLB为

根据约束条件可计算得到

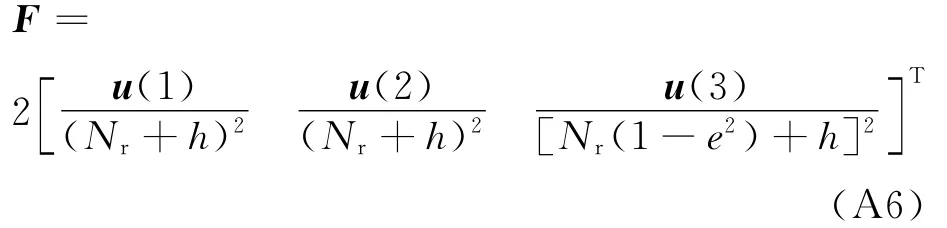
4)运动目标约束CRLB

由文献[21]可知,当存在额外的约束条件时

其CRLB为

CRLB(θ)=J-1-J-1F(FTJ-1F)-1FTJ-1(A8)

式中:F为约束条件关于估计量的梯度,即

Semidefinite programming algorithm with TDOA and FDOA measurements based on WGS-84 earth model

Ll Wanchun1,2,*,PENG Wuke1,3,PENG Li1,MA Yezi1,Ll Yingxiang2

1.Center for Cyber Security,School of Electronic Engineering,University of Electronic Science and Technology of China,Chengdu 611731,China;
2.Meteorological lnformation and Signal Processing Key Laboratory of Sichuan Higher Education lnstitutes,School of Communication Engineering,Chengdu University of lnformation Technology,Chengdu 610225,China;
3.School of Medicine,Tsinghua University,Beijing 100084,China

ln essence,detecting the location and velocity of a radiation source by utilizing time difference of arrival/frequency difference of arrival(TDOA/FDOA)for multiple satellites can be deemed as a highly nonlinear solution problem within noise.For a ground target,the WGS-84 earth model is the constraint condition,which makes the location system become more complicated.ln this paper,a new algorithm for solving this location problem is proposed based on the semi-definite programming(SDP).Based on the novel algorithm,the nonlinear location problem can turn into a semidefinite optimization(SDO)by an appropriate relaxation which can be solved by some mature software like CVX.According to this model,the Cramer-Rao Lower Bound(CRLB)of the location problem is then given.The computer simulation demonstrates that the proposed algorithm can approach the CRLB effectively.

WGS-84 earth model;location by time difference of arrival,location by frequency difference of arrival;semidefinite programming;Cramer-Rao lower bound

2016-10-12;Revised:2016-11-28;Accepted:2017-03-17;Published online:2017-04-01 13:27

URL:www.cnki.net/kcms/detail/11.1929.V.20170401.1327.002.html

Meteorological lnformation and Signal Processing Key Laboratory of Sichuan Higher Education lnstitutes

V19;TN967.1

A

1000-6893(2017)07-320843-08

10.7527/S1000-6893.2017.320843

2016-10-12;退修日期:2016-11-28;录用日期:2017-03-17;网络出版时间:2017-04-01 13:27

www.cnki.net/kcms/detail/11.1929.V.20170401.1327.002.html

气象信息与信号处理四川省高校重点实验室基金

*通讯作者.E-mail:liwanchun@uestc.edu.cn

李万春,彭吴可,彭丽,等.WGS-84模型下时差频差半定规划定位算法[J].航空学报,2017,38(7):320843.Ll W C,PENG W K,PENG L,et al.Semidefinite programming algorithm with TDOA and FDOA measurements based on WGS-84 earth model[J].Acta Aeronautica et Astronautica Sinica,2017,38(7):320843.

(责任编辑:苏磊)

*Corresponding author.E-mail:liwanchun@uestc.edu.cn