四旋翼飞行器的LQR优化控制

北京信息科技大学自动化学院，北京 100192

一、引言

随着无人机地快速发展，无人机巡检技术以其良好的特性成为各大公司的巡检利器，并大大减少了维护成本。为了便于对巡检位置上的故障分析诊断，无人机巡检时要求拍摄高清晰度的照片，因此，巡检时要求无人机要尽可能地靠近巡检对象，但是距离越近，必然存在另一方面的安全隐患，若不对其速度和飞行姿态，飞行方向加以控制，就很有可能撞上巡检对象，所以研究巡检无人机的优化飞行控制具有重要的工程应用意义。

在巡检无人机中，四旋翼飞行器具有结构简单、成本低、轻小易携带、能垂直起降、可实现六自由度等优点，因而可以看作是一种良好的飞行控制算法验证平台。它除了具备一般无人机隐蔽性好、生命力强、造价低廉、操控简单、起降稳定的优点以外，其特殊的结构使其还有以下优点[1-5]。

1、飞行器体积小、方便携带，适合多平台、多空间的应用，可以在地面、军舰上自由灵活地垂直降，无需发射架、弹射器等辅助装置；

2、具备良好的机动性，能快速、灵活地在三维空间进行运动，可大大缩小旋回半径，从而可以节省时间、提高效率；

3、结构简单、便于操控，可执行诸如军事侦察、目标锁定、航拍、森林救火、重点区域安防巡逻等各种特殊、危险的任务。

本文以四旋翼飞行器作为研究对象，在原有的线性二次最优控制算法的基础上，采用LQR优化控制算法，该算法保证了无人机在巡检过程中其飞行控制系统的稳定性，以及面对不同干扰信号良好的抗干扰性能。

二、四旋翼飞行器的数学模型

图1所示为四旋翼飞行器结构模型图。从该结构模型可以看出，四旋翼飞行器是通过分布于四周的电机（M1，M2，M3，M4）的转速调整来实现俯仰、滚转、偏航运动的，并且四个电机承担着提供升力的任务。通过改变4个电机的转动速度，我们可以控制飞行器的垂直起降运动。其中，M1和M3将为飞行器的俯仰运动提供力矩；M2和M4为飞行器的滚转运动提供力矩；M1、M2、M3、M4共同作用将实现飞行器的偏航运动。

下面研究如何根据飞行器的动力学特性建立其数学模型。

首先，建立空间坐标系A(OXYZ)和机体坐标系B(oxyz)如图2所示。并做如下假设[1-5]：

1、四旋翼飞行器是完全均匀对称的刚体结构；

2、四旋翼飞行器的几何中心和重心重合；

3、四旋翼飞行器飞行时其飞行姿态角变化很小；

4、直流电机的输入电压和输出力矩之间呈线性关系。

在这些假设条件下，可以把四旋翼飞行器的动力学模型等效成一个固定的飞行器在空中由电机转子转动而引起的空气动力学特性。

利用牛顿第二定律，该四旋翼飞行器的动力学模型为[1]：

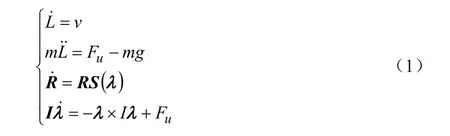
其中，L—表示四旋翼飞行器的质心到空间坐标系原地的距离；

m—表示四旋翼飞行器的总质量；

Fu—4个电机的合力；

λ—表示四旋翼飞行器相对于机体坐标系中的旋转角速度，其具体表达式如下：

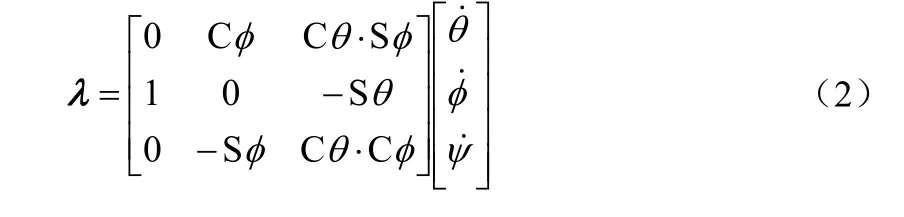
（C和S分别代表三角函数cos和sin）

在小角度情况下，λ可近似为即：

式中，θ—表示四旋翼飞行器的纵轴(oz)与水平面(OXY)的夹角，为俯仰角，若飞行器纵轴指向水平面上方，则θ为正，反之为负；

φ—表示B坐标系的坐标轴与包含四旋翼飞行器纵轴(oz)的铅垂直平面的夹角，为滚转角，由飞行器尾部顺纵轴前视，若(oz)纵轴位于铅垂面右侧（即飞行器向右倾斜），则φ为正，反之为负；

Ψ—为四旋翼飞行器纵轴在水平面内投影与空间坐标系(OX)轴之间的夹角，为偏航角，前视Ψ角平面，若由(OX)轴转至投影线为逆时针旋转，则Ψ为正，反之为负。

I∈R3×3—表示为坐标系B中机体的转动惯量：

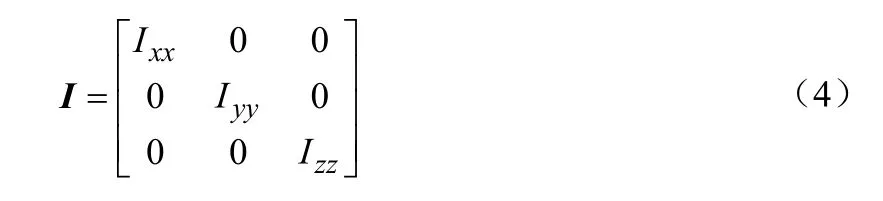
式中，Ixx，Iyy，Izz—分别为机体绕三坐标轴的转动惯量；

R—表示一个3×3阶的方向余弦矩阵[1-2]，表示从空间坐标系到机体坐标系的转换矩阵[3-4]：

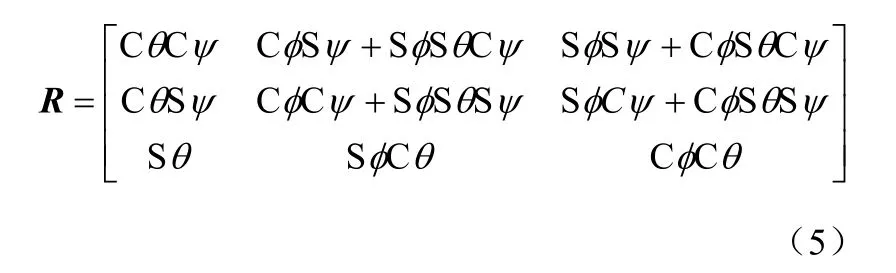
（C和S分别代表三角函数cos和sin）

对于给定的列向量λ=[λ1λ2λ3]T，定义S(λ)为：

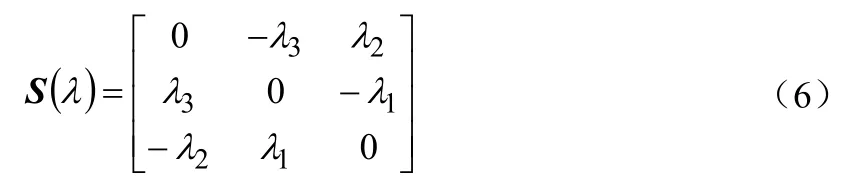
综上所述，空间坐标系下的四旋翼飞行器的数学模型为：

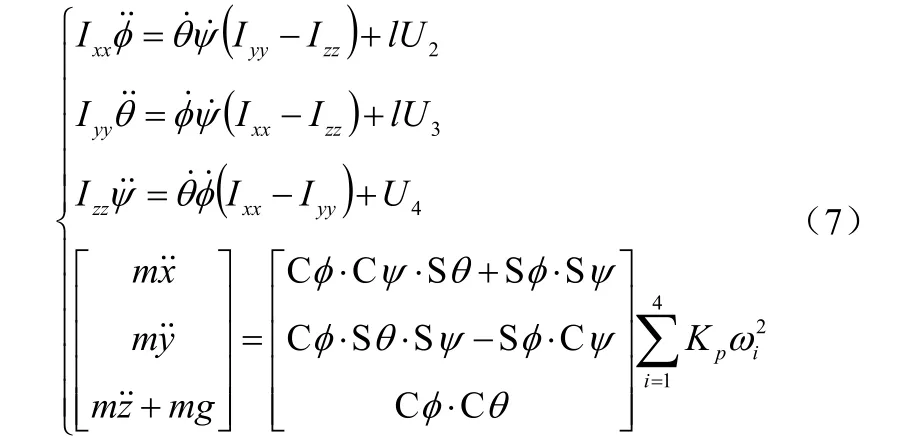
（C和S分别代表三角函数cos和sin）

其中，l—机体几何中心距电机安装中心的距离；

Kp—升力系数，

ωi—旋转角速度；

U1,U2,U3,U4——4个电机的角速度决定的系统的控制输入量，具体如下：

式中，Kd—拖拉系数。

旋翼由无刷直流电机驱动，直流电机电枢回路的电压平衡方程和电机转动的力矩平衡方程为[1]：

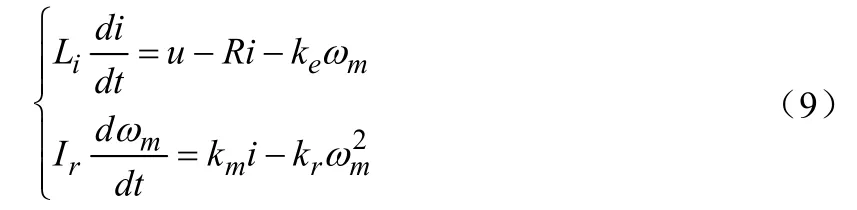
式中，u—电机输入电压；

i—电机输入电流；

ke—反电势系数；

km—电机转矩系数 ；

kr—负载转矩常量；

R—电机本身阻抗；

Ir—电机的惯性常数。

由于四旋翼飞行器使用的小型直流电机具有很低的感应系数，故感应系数Li可以忽略不计，式（9）可以近似为：

三、四旋翼飞行器的LQR优化控制

根据四旋翼飞行器的特点和动力学特性，我们选择LQR控制方法，LQR控制是在规定的限度下，使被控系统的性能指标达到最佳状态的控制；即在满足一定的约束条件下，寻求最优控制策略，使得系统性能指标取得极大值或极小值。

定理1对于给定的受控系统[7]：

以及其性能指标：

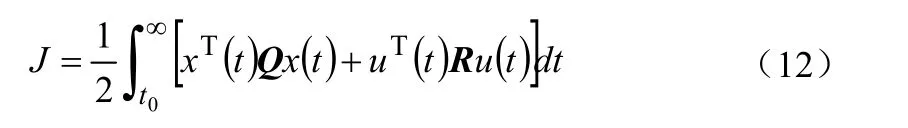
其中，Q、R—定常对称正定矩阵。

设[A,B]可控，则存在唯一的最优控制：

最优性能指标简化为：

式中，x*(t0)=x0，它所对应的最优轨迹是式（15）的解x*(t)：

“城市复兴”视角下的古城更新规划探索——以许昌曹魏古城城市设计为例 滕 熙 张 萍2018/04 40

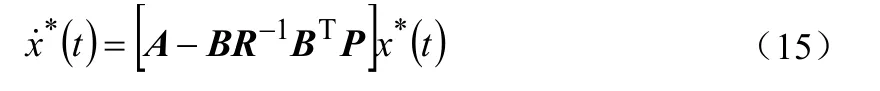
矩阵P为Riccati代数方程的唯一对称正定解。

式中，A—系统的系数矩阵；

B—系统的输入矩阵；

Q,R—给定的定常对称正定矩阵；

K—最优反馈增益矩阵。

定理2设[A,B]可控，[A,C]可观，R〉0，Q=DT，D≥0，则受控系统式（11）在指标式（12）下的最优控制为：

它所对应的最优轨迹为式（18）的解x*(t)：

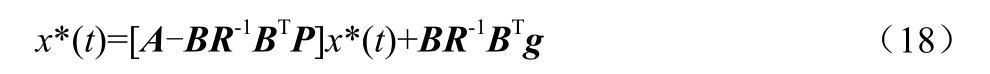
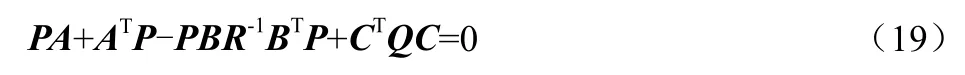
而常数向量为：

其中，yr—参考信号，即期望信号。

将所建立的数学模型式（7）表示为状态空间表达式为：

（C和S分别代表三角函数cos和sin）

其中，θ、φ、Ψ—分别为俯仰角、滚转角、偏航角；

Ixx，Iyy，Izz—分别为滚转转动惯量、俯仰转动惯量、偏航转动惯量；

kfc—电压与升力比；

l1—前向升力距质点的距离；

ω—左右臂与X轴的夹角；

U1,U2,U3,U4—分别为前向电机电压、左向电机电压、右向电机电压、后向电机电压。输出为：

目标函数可以写为：

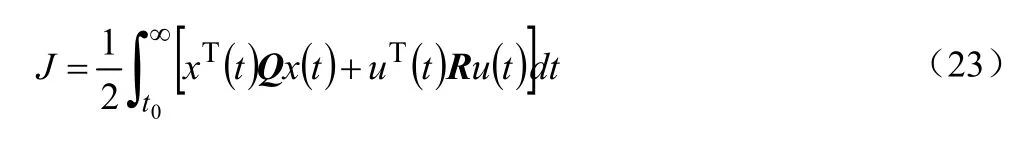
R，Q分别为系统输入向量和状态向量的定常正定对称矩阵，根据实际需求要对系统实现最优控制，需要在控制输出间寻找一个最优平衡状态。经过多次仿真测试与多次试验，取R=diag[1,1,1,1]，Q=diag[10,2.8,5.1,2,1,0.1]，此时能够得到较优的控制效果。若要使得上述性能指标最小化，可由定理1中的Riccati方程求出矩阵P，并找出状态反馈控制律：即当四旋翼飞行器趋于稳定时，可实现系统输出跟踪期望输出[9]。

四、四旋翼飞行器LQR优化控制仿真

1、LQR优化控制器对未加干扰信号的跟踪情况

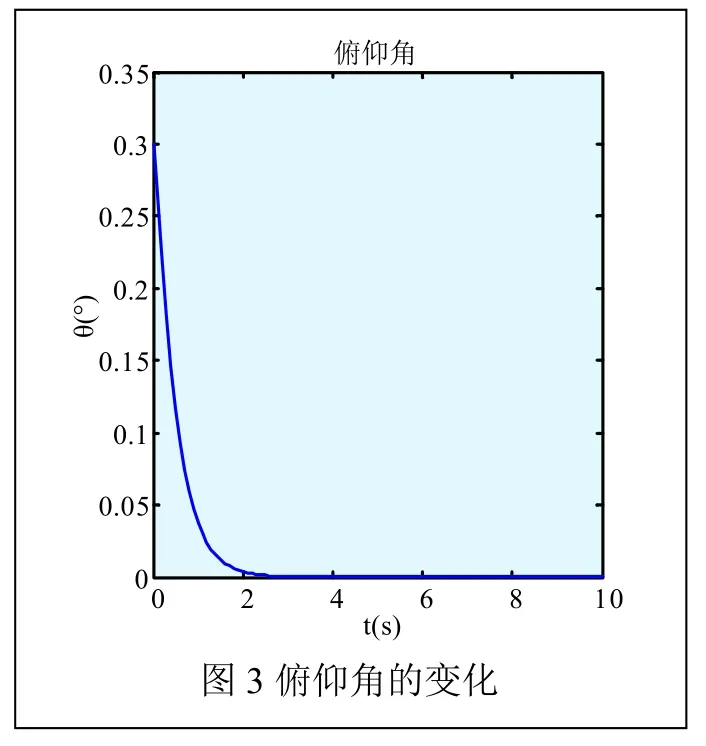
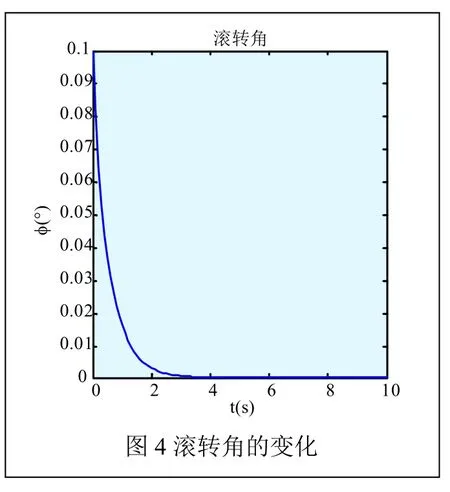
根据所建立的四旋翼飞行器的模型，仿真结果如图3～图5所示。假设此时的俯仰角、滚转角、偏航角的期望输出为0°。

由图3、图4、图5可以看出，在初始运行阶段，系统在初始状态随着LQR控制器的控制参数K的调节作用，经过很短时间的动态调节过程后，其俯仰角、滚转角、偏航角即可准确地跟踪系统的期望输出。

2、LQR优化控制器对加入阶跃信号作为干扰信号的跟踪情况

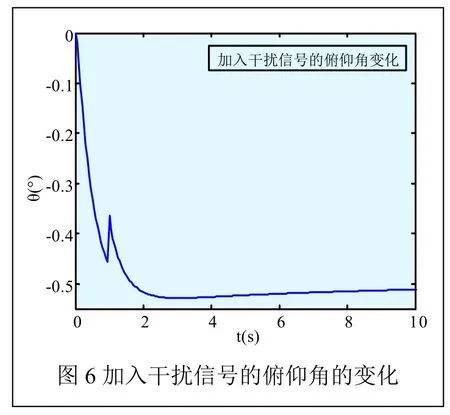
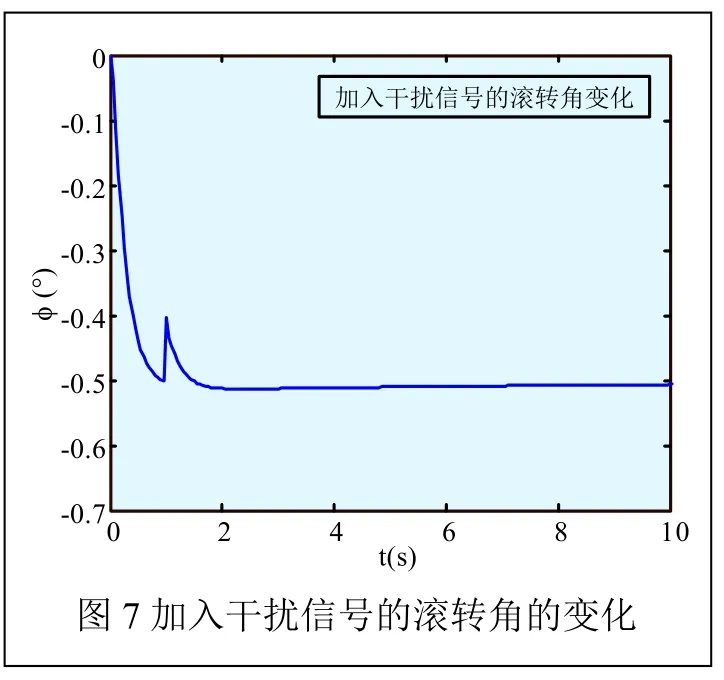
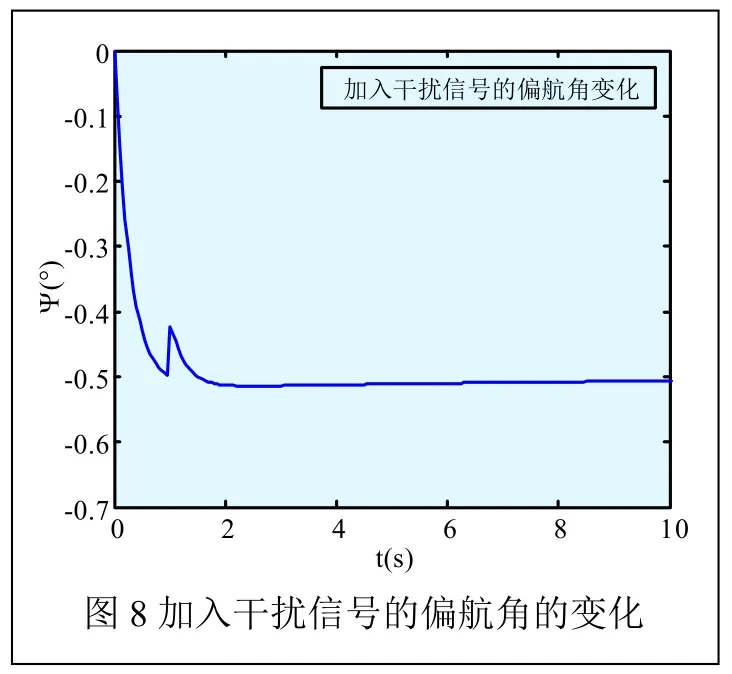
为考察所设计的控制器对阶跃信号的抗干扰性能，我们进行假设，假设俯仰角、滚转角、偏航角的期望值为-0.5°，在所设计的LQR控制器中加入幅值为0.1的阶跃信号作为干扰，我们可以得到仿真图如图6～图8所示。

从图6、图7、图8可以很明显地看出，在初始运行状态，我们在系统中加入阶跃信号作为干扰信号时，系统会随着所设计的LQR控制器在反馈矩阵K的调节作用下，经过较短的动态调节过程后，该系统最终达到稳定状态，即俯仰角、滚转角、偏航角可以准确地达到系统所期望的值，并且曲线几乎没有波动，从而说明了所设计的LQR优化控制器具备一定的阶跃信号抗干扰能力。

3、LQR优化控制器对加入白噪声作为干扰信号的跟踪情况

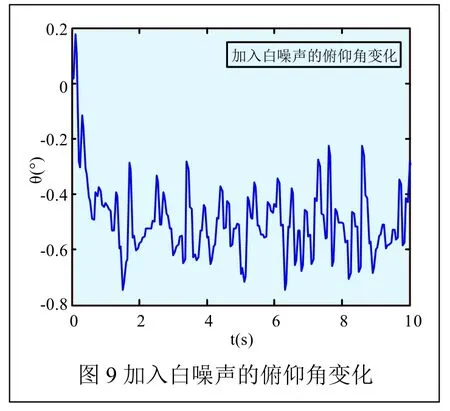
为考察所设计的控制器的对白噪声信号的抗干扰性能，我们进行假设，假设俯仰角、滚转角、偏航角的期望值为-0.5°，在所设计的LQR控制器中加入幅值为0.1的白噪声信号作为干扰，我们可以得到仿真图图9～图11。

从图9、图10、图11可以很明显地看出，在初始运行状态，我们在系统中加入幅值为0.1的白噪声作为干扰信号时，系统会随着所设计的LQR控制器在反馈矩阵K的调节作用下，经过动态调节过程后，该系统最终达到相对稳定状态，即俯仰角、滚转角、偏航角可以达到系统所期望的值，但是曲线波动较大，说明了所设计的LQR优化控制器在一定条件下相对具备对白噪声抗干扰能力。

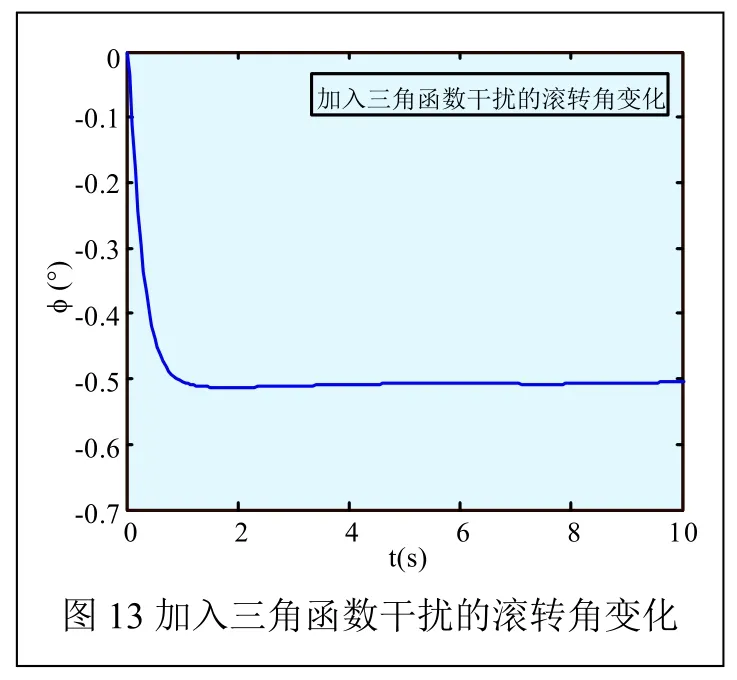
4、LQR优化控制器对加入三角函数作为干扰信号的跟踪情况

为考察所设计的控制器的对三角函数信号的抗干扰性能，我们进行假设，假设俯仰角、滚转角、偏航角的期望值为-0.5°，在所设计的LQR控制器中加入幅值为0.1的三角函数信号作为干扰，我们可以得到仿真图如图12～图14所示。

从图12、图13、图14可以很明显地看出，在初始运行状态，我们在系统中加入幅值为0.1的三角函数作为干扰信号时，系统会随着所设计的LQR控制器在反馈矩阵K的调节作用下，经过短暂的动态调节过程后，该系统最终达到稳定状态，即俯仰角、滚转角、偏航角可以很准确地达到系统所期望的值，并且曲线几乎没有波动，说明了所设计的LQR优化控制器对三角函数具备良好的抗干扰能力。

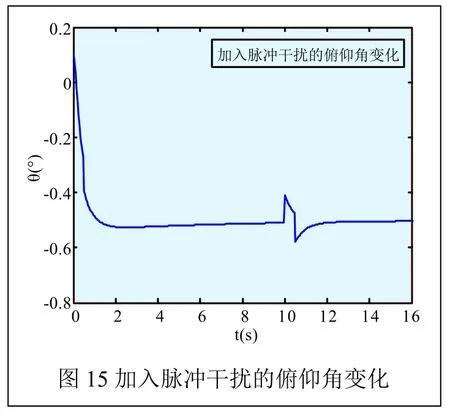
5、LQR优化控制器对加入脉冲函数作为干扰信号的跟踪情况

为考察所设计的控制器的对脉冲函数信号的抗干扰性能，我们进行假设，假设俯仰角、滚转角、偏航角的期望值为-0.5°，在所设计的LQR控制器中加入幅值为0.1的脉冲信号作为干扰，我们可以得到仿真图如图15～17所示。

从图15、图16、图17可以很明显地看出，在初始运行状态，我们在系统中第10s时加入幅值为0.1的脉冲函数作为干扰信号时，系统会随着所设计的LQR控制器在反馈矩阵K的调节作用下，经过短暂的动态调节过程后，该系统最终达到稳定状态，即俯仰角、滚转角、偏航角可以很准确地达到系统所期望的值，并且曲线几乎没有波动，说明了所设计的LQR优化控制器对脉冲函数具备良好的抗干扰能力。

五、结束语

本文以四旋翼飞行器为研究对象，建立了四旋翼飞行器的数学模型，以LQR控制理论为基础，设计了四旋翼飞行器的最优控制算法，进行了仿真，并对多个干扰信号进行抗干扰性能考察，从仿真结果看，系统总体呈现稳定状态，运动过程中，四旋翼飞行器的俯仰角、滚转角、偏航角都能较快速地趋于稳定，取得了良好的控制效果及控制精度，并且对阶跃信号、白噪声、三角函数干扰、脉冲信号具备一定的抗干扰性能。仿真结果验证了所设计的LQR优化控制器的有效性、可靠性、准确性。