半封闭海湾共振周期计算与研究

杨万康, 伊小飞, 陈忠彪



半封闭海湾共振周期计算与研究

杨万康1, 伊小飞2, 陈忠彪3

(1. 国家海洋局第二海洋研究所工程海洋学重点实验室, 浙江杭州 310012; 2. 广东海洋大学海洋与气象学院, 广东湛江 524088; 3. 南京信息工程大学海洋科学学院, 江苏南京 210044)

三门湾海域水波共振现象较为显著, 容易引发海洋灾害。针对三门湾这一典型半封闭海湾, 分别从理论推导和数值模拟两方面研究了三门湾的共振周期。研究发现: 理论推导结果可以用于对海湾整体共振周期的粗略估计, 数值模拟结果更加精确, 也能充分反映海湾内不同水域的共振特征。数值模拟结果表明, 三门湾内各水域普遍存在3~4个共振周期模态, 湾内各水道第一模态和第三模态共振周期数值解与理论值较为接近, 石浦水道与外海相联通, 共振周期不显著。三门湾内各水域共振周期第一模态对应的振幅最大, 然后依次递减, 但湾顶的青山港、蛇蟠水道第二模态共振周期及对应的振幅值与第一模态相差较小, 基本呈现双峰结构。共振振幅由湾外向三门湾顶部逐渐增加, 尤其是湾顶处振幅增益比较显著。通过本研究可以为三门湾的防灾减灾提供科学依据。

半封闭海湾; 共振; 理论推导; 数值模拟

共振是海洋中普遍存在的现象。尤其是对于沿岸的海湾地区, 共振现象会造成沿岸水位的暴增, 造成严重的海洋灾害, 因此是海洋动力学研究的热点之一。

海湾的共振周期取决于海湾的水深和形状, 关于海湾共振周期的研究, 19世纪20年代就有了著名的梅立恩公式, 这一公式的不足之处是要求海湾形状和深度具有很规则的变化或简单地看作常数, 这与实际情况有所出入。Proudman[1]认为芬迪湾较强的半日潮与潮波共振有关, 即1/4波长共振理论; 方国洪等[2]通过研究发现北部湾较强的全日潮是由于共振造成的, 通过理论推导得到海湾共振周期约为28.9 h, 与全日潮的周期较为接近, 因此全日潮振幅的增益较为显著。Cummins等[3]认为哈德逊海峡的共振情况与半波长共振较为接近, 考虑了昂加瓦湾和科氏力的影响, 最终估算共振周期约为9.5~10.5 h。王钟桾等[4]利用二维数值模式, 计算了芝罘湾的固有周期, 与实测资料吻合较好。Webb[5]提出了一种边值方法用于计算海湾的共振周期, 通过在开边界处添加不同周期的波动, 然后选取湾内振幅极大值对应的周期为共振周期。Grean等[6]利用数值模型计算了胡安德富卡海峡和乔治亚海峡的共振周期约为16 h, 认为Helmholtz共振模型更符合该海区情况。Wilson[7]认为, 沿岸假潮现象在许多情况下是一种强迫共振或者近似共振现象, 当长周期波进入湾口时, 是比较明显的强迫振动, 当外强迫消失后, 就转变为自由震荡, 而且是以海湾的固有周期继续振动。Wong[8]在长岛海湾的研究中发现, 由于共振效应, 半日分潮的振幅增加了4倍; Clarke等[9]通过简化拉普拉斯方程, 推导了共振发生的前提条件; Bertin等[10]采用大陆架共振理论模型和数值实验两种方法研究发现数值模型计算结果能够较好的匹配实际现象。一般而言, 对于实际海域共振周期的计算, 理论方法主要基于1/4波长和 Helmholtz模型共振; 数值计算方面主要有简正模态方法和边值方法[11]。

三门湾位于浙江象山县南田岛和三门县牛头山之间, 是一个西北-东南方向的半封闭海湾, 从湾口到湾顶长约40 km, 湾内多数地区宽10 km, 除东南方向通过石浦水道与外海连通外, 其余则为陆地和海岛包围, 具体地理位置如图1所示。属于较为典型的半封闭海湾, 潮汐周期受到外海的支配, 当潮波进入海湾后, 受到湾顶的反射, 从而形成驻波, 产生共振。此前关于三门湾共振特征的研究较少, 本文将分别采用理论推导和数值模拟方法来研究分析三门湾内的共振周期, 通过建立高分辨的数值模型, 对三门湾内各水道的共振周期特征进行精细化研究。

图1 三门湾地理位置及水深(单位: m)示意图

1 理论推导

据文献[12], 早在1828年, Merian在研究湖泊共振时提出了1/4波长共振理论, 针对只存在一个封闭波节的封闭水域, 共振周期计算公式为:

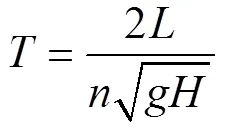
其中,、、、分别表示海湾长度、任意整数、重力加速度、水深。

经典的梅里恩公式要求研究区域为完全封闭的海湾、湖泊, 由于三门湾为半封闭海湾, 因此需要对梅里恩公式进行一定的改进才能适用于三门湾海域。

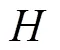
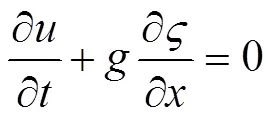
根据上述两个方程可以得到

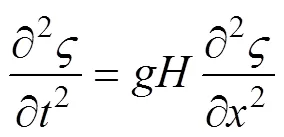
这是典型的波动方程, 解的形式一般为

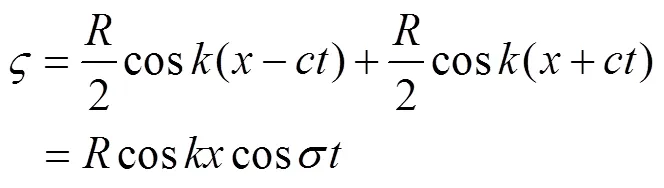
利用关系式

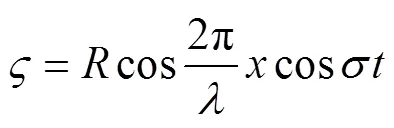
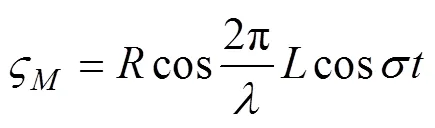
则代入公式(6)可以得到:

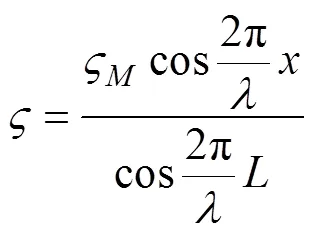
所以共振发生的条件是

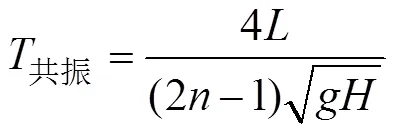
假设三门湾长度为38 km, 平均水深取为7 m, 其共振周期理论结果如表1所示, 由理论推导的结果可知, 三门湾的共振周期理论解有无数个, 周期最大的为5 h, 其余分别为1.67, 1 h, ……, 由于理论计算假设水深为固定值, 三门湾实际形状也简化为矩形海湾, 因此结果可能有一定的误差, 后面将利用更为准确的数值模拟方法推算三门湾的共振周期。

2 数值模拟方法

理论方法通过概化海湾形状、水深地形等条件, 可以用于许多海域共振周期的粗略估计。但是由于推导过程中采用了大量的近似及假设条件, 与实际情况存在一定的误差, 尤其是理论推导方法不能反映海湾内各局部地区的共振周期特征, 因此根据海湾内的实际情况, 本文采用数值模拟方法对三门湾内的共振周期特征进行研究分析。

表1 三门湾共振周期理论解

2.1 模型设置与验证

本文数值模型采用了MIKE21数学模型, 该模型可以很好地模拟河流、海湾及海洋的水流、波浪、泥沙及水质环境等, 在近岸港湾地区得到广泛应用[13-14]。本模型计算区域如图2所示, 网格采用非结构三角形网格, 共有100 079个网格单元, 海湾内分辨率为20 m左右, 水深地形采用实际工程测量水深与海图资料, 计算步长采用动态步长, 范围为0.01~1 s。模型验证采用三门湾内的实测潮位站数据, T1、T2、T3潮位站位置如图3所示。模型验证结果如图4所示, 可以看到模拟振幅和实测振幅符合较好, 相位误差较小, 表明该模型能准确反映海湾内的水位变化特征。

图2 研究区域网格划分示意图

2.2 数值模拟结果与分析

各代表计算点随开边界入射波周期变化的振幅曲线如图5所示, 由图可知, 各计算点振幅曲线存在多个极大值, 各曲线振幅极大值对应于共振周期的不同模态, 其中共振周期数值最大的为第一模态, 随着模态的递增, 共振周期的数值依次递减。不同模态的共振周期统计结果如表2所示。由数值模拟结果可知:

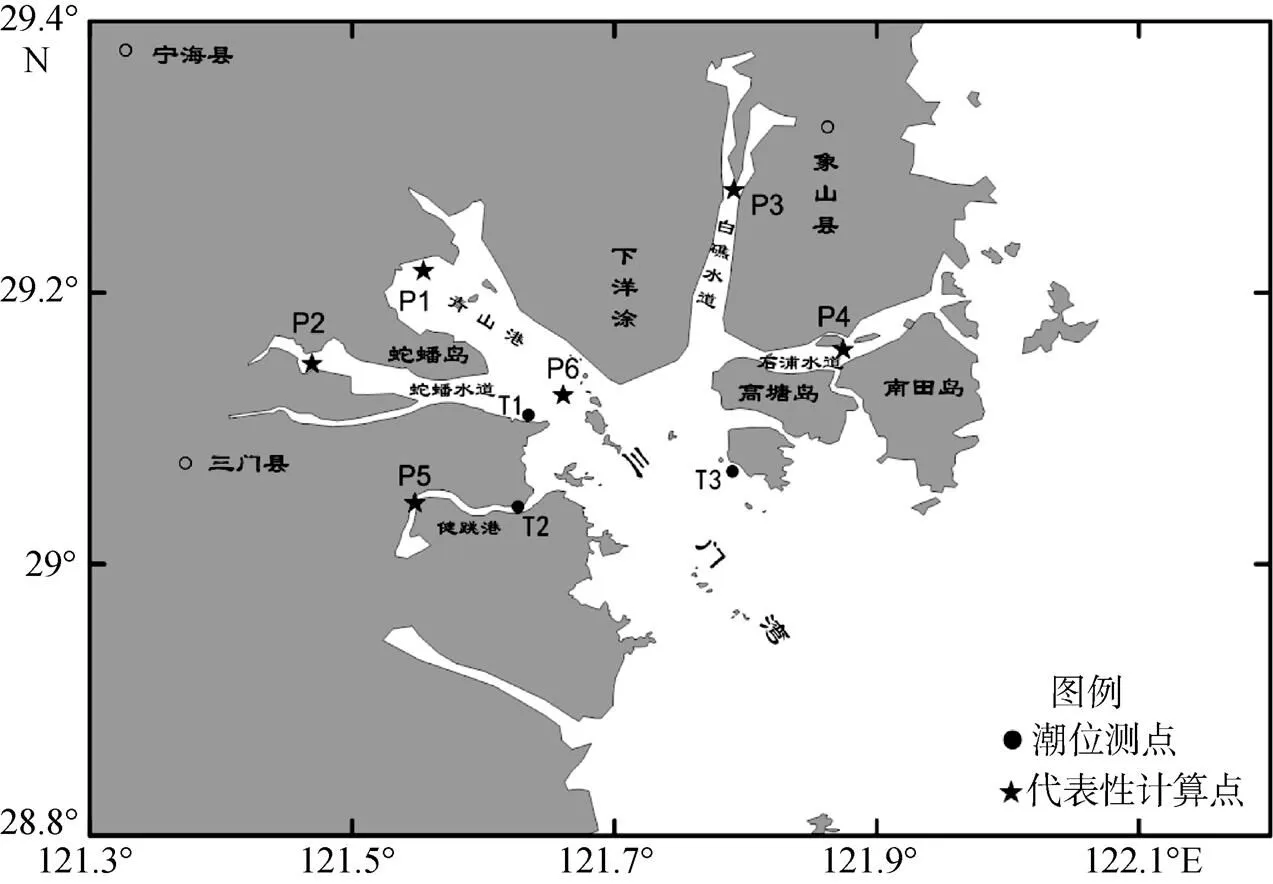
图3 海湾内代表性计算点及实测潮位站分布图

图4 模拟潮位与实测潮位对比

图5 各计算点振幅随周期的变化

表2 各水道共振周期数值模拟结果(单位: h)

1) 三门湾内各水域的实际共振周期模态要远少于理论推导得到的模态个数, 至多存在4~5个模态, 这是由于数值模拟考虑了实际的岸线阻挡及底摩擦消耗等因素, 尤其是理论推导中的高频共振在实际条件下不会发生。

2) 除了白礁水道和石浦水道外, 其他区域的共振周期第一模态与理论值相差较小, 青山港和蛇蟠水道与理论值一致, 为5.0 h, 健跳水道和三门湾中心位置都为5.5 h。石浦水道由于与外海相联通, 并非一个完整的半封闭水道, 因此共振周期第一模态不是非常显著, 大约为6.5 h。白礁水道位于三门湾内部, 但是其走向与三门湾走向夹角较大, 几乎呈现垂直状态, 相当于是两个半封闭海湾的嵌套, 因此共振周期要大于三门湾的理论值。

3) 数值模拟结果的第二模态共振周期与理论值相差较大, 湾顶处的青山港, 蛇蟠水道第二模态周期值为3.0~3.17 h, 而理论推导无此共振周期结果。石浦水道是因为与外界水流的相互作用存在一个2.5 h的周期。数值模拟结果显示各水道的第三模态周期为1.67 h, 与理论值计算结果基本一致。白礁水道、健跳水道和三门湾中心第4模态周期为0.67 h, 青山港和蛇蟠水道第5模态共振周期为0.33 h。

4) 从各个计算点的振幅来看, 第一模态振幅最大, 然后依次递减, 但位于湾顶的青山港, 蛇蟠水道不仅共振周期有一定的特殊性, 其第二模态的共振振幅与第一模态振幅相差较小, 基本呈现双高峰结构, 其他水道则无此特征, 随着模态的增加, 振幅迅速减小。

5) 由于第一模态为三门湾内所有水域普遍具有的共振特征, 而且振幅最为显著, 因此本文计算了在第一模态共振周期下, 整个海湾的振幅增益如图6所示。由图可知, 共振振幅由湾外向三门湾内部逐渐增加, 假定开边界处振幅为1.0 m, 在湾顶处振幅达到了3.5~4.0 m, 石浦水道共振振幅为1.5~2.0 m, 健跳水道和白礁水道振幅为2.5~3.0 m。通过本研究可知如果三门湾外海产生的扰动周期正好与海湾的共振周期一致, 即使外海的波动振幅较小, 由于较强的振幅增益, 也会对三门湾内沿岸造成严重的灾害。

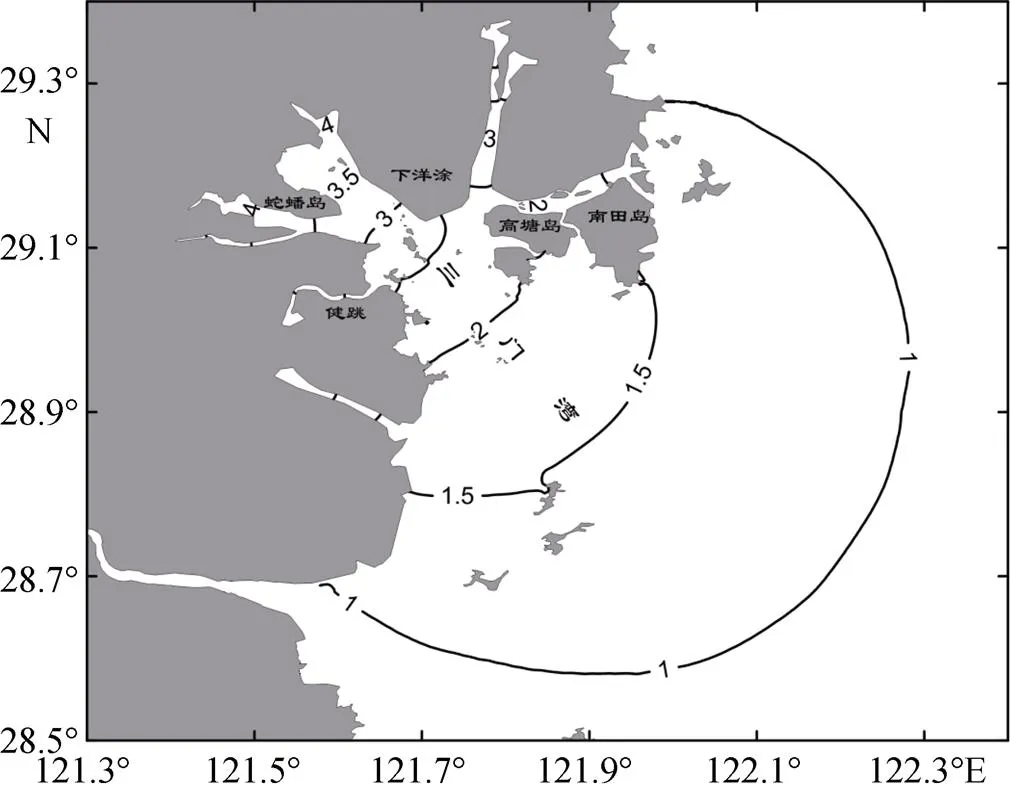
图6 第一模态共振周期对应的振幅增益(单位: m)

3 结语

本文分别采用理论推导和数值方法研究了三门湾的共振特征, 通过建立高分辨率的数值模型, 能够对三门湾内各水道的共振周期进行精细化研究, 数值模拟结果比理论解更加准确。研究发现三门湾内各水域普遍存在4~5个共振周期模态, 各水道第一模态和第三模态共振周期与理论值比较接近, 石浦水道由于与外海相联通, 并非一个完整的半封闭水道, 因此共振周期不是非常显著。三门湾内各水域共振周期第一模态对应的振幅最大, 然后依次递减, 但湾顶的青山港, 蛇蟠水道, 其第二模态共振周期及对应的振幅与第一模态相差较小, 基本呈现双峰结构。通过计算在第一模态共振周期下整个海湾的振幅增益可知, 共振振幅由湾外向三门湾内部逐渐增加, 尤其是湾顶处振幅会有显著的增加, 因此如果外海的扰动, 正好与海湾的共振周期一致, 由于较强的振幅增益, 可能会在三门湾内造成严重的灾害, 因此下一步需要结合实际观测资料进行更加细致深入的研究。

[1] Proudman J. Oscillations of tide and surge in an estuary of finite length[J]. Journal of Fluid Mechanics, 1957, 2(04): 371-382.

[2] Cui X, Fang G, Teng F, et al. Estimating peak response frequencies in a tidal band in the seas adjacent to China with a numerical model[J]. Acta Oceanology Sinica, 2015, 34(1): 29-37.

[3] Cummins P F, Karsten R H, Arbic B K. The semi-diu­rnal tide in Hudson strait as a resonant channel oscillation[J]. Atmosphere-ocean, 2010, 48(3): 163-176.

[4] 王钟桾, 龙宝森. 半封闭海湾固有振动周期的数值计算[J]. 海岸工程, 1998, 4: 1-4. Wang Zhongjun, Long Baosen. Computations of natural periods of a half-closed bay using a numerical model[J]. Coastal Engineering, 1998, 4: 1-4.

[5] Webb D J. On the shelf resonances of the Gulf of Carpentaria and the Arafura Sea[J]. Ocean Science, 2012, 8(5): 733.

[6] Crean P B, Murty T S, Stronach J A. Mathematical modelling of tides and estuarine circulation: The coastal seas of southern British Columbia and Washington state[M]. Berlin: Springer-Verlag, 1988: 471-472.

[7] Wilson B S. The Encyclopedia of oceanography[M]. New York: Academic Press, 1966: 804-817.

[8] Wong K C, Moses Hall J E. On the relative importance of the remote and local wind effects to the sub tidal variability in a coastal plain estuary, Journal of Geophysical Research: Oceans, 1998, 103(C9): 18393- 18404.

[9] Clarke A J, Battisti D S. The effect of continental shelves on tides[J]. Deep Sea Research Part A. Oceano­graphic Research Papers, 1981, 28(7): 665-682.

[10] Bertin X, Bruneau N, Breilh J F, et al. Importance of wave age and resonance in storm surges: The case Xynthia, Bay of Biscay[J]. Ocean Modelling, 2012, 42: 16-30.

[11] 崔欣梅, 方国洪, 滕飞, 等. 芬迪湾、缅因湾和圣劳伦斯湾潮汐共振的数值研究[J]. 海洋科学进展, 2015, 33(1): 11-18. Cui Xinmei, Fang Guohong, Teng Fei, et al.Numerical study on tidal resonances in the bay of Fundy, the Gulf of Maine and the Gulf of Saint Lawrence[J]. Advances in Marine Science, 2015, 33(1): 11-18.

[12] Proudman J. Dynamical Oceanography[M]. London: Methuen, 1953: 85-89.

[13] 刘潇, 冯秀丽, 刘杰. 港口工程影响下莱州湾西南侧海域水动力演化特征[J]. 海洋科学, 2016, 40(3): 138-145. Liu Xiao, FengXiuli, Liu Jie. Hydrodynamic evolution characteristics of southwest Laizhou Bay under the effect of port construction[J]. Marine Sciences, 2016, 40(3): 138-145.

[14] 周广镇, 冯秀丽, 刘杰, 等. 莱州湾东岸近岸海域规划围填海后冲淤演变预测[J]. 海洋科学, 2014, 38(1): 15-19. Zhou Guangzhen, Feng Xiuli, Liu Jie, et al.Prediction of erosion evolution and deposition in the east coast of the Laizhou Bay after the implementation of the coastal planning[J]. Marine Sciences, 2014, 38(1): 15-19.

Calculation and study of resonant period in semi-closed bay

YANG Wan-kang1, YI Xiao-fei2, CHEN Zhong-biao3

(1. Key Laboratory of Engineering Oceanography, the Second Institute of Oceanography, State Oceanic Administration, Hangzhou 310012, China; 2. College of Ocean and Meteorology, Guangdong Ocean University, Zhanjiang 524088, China; 3. College of Marine Science, Nanjing University of Information Science and Technology, Nanjing 210044, China)

The wave resonance phenomenon is significant in Sanmen Bay and leads to many marine disasters. As a typical semi-closed bay, we investigated the resonance period of Sanmen Bay by theoretical formulation and numerical simulation. We found the theoretical formula to be of use in estimating the resonance period of the bay but the numerical simulation results were more accurate and reasonable, because the differences in the resonance characteristics of the bay waters can be described in greater detail. The numerical results show there to be 4–5 resonant period modes in Sanmen Bay, and the numerical simulation solutions of the first and third modal resonance periods are close to the theoretical values. The Shipu waterway is connected with the offshore region, so its resonance period is not significant. The first mode amplitude of the resonance period is the largest and then it decreases with increasing mode, but there is only a slight difference between the first and second modes with respect to the period and amplitude values of the Qingshan port and Shepan waterway, which show a bimodal structure. The resonant amplitude gain gradually increases from outside to the inside of the bay, and is especially significant at the top of bay. Through this study, we have established a scientific basis for Sanmen Bay disaster prevention.

semi-closed bay; resonance; theoretical derivation; numerical simulation

(本文编辑: 李晓燕)

P731.23

A

1000-3096(2017)07-0071-07

10.11759/hykx20170311001

2017-03-11;

2017-05-16

广东海洋大学近海海洋变化与灾害重点实验室开放基金(GLOD1405)

[Guangdong Key Laboratory for Coastal Ocean Variation and Disaster Prediction open Foundation, No.1405]

杨万康(1987-), 男, 山东青州人, 汉族, 工程师, 主要从事海洋预报和数值模拟工作, 电话: 0571-89715123, Email: yangwankang@126.com

Mar. 11, 2017