建构数的表象 丰富数的内涵

居海霞

摘 要：建立数的表象，是帮助学生深刻认识数的内涵的重要桥梁。只有对数的表征认识清楚、到位，才能在具体、直观的基础之上逐步抽象，最终真正建立起数的概念，理解数的意义。文中，笔者从整数、小数和分数三种数的认识出发，分别阐述如何帮助学生建立数的表象，从而丰富数的内涵。

关键词：表象；数的内涵；推算感知；形中蕴数；逐步抽象

表象是一种心理现象，人们感知过的某一事物，其形象常常会在头脑中以痕迹的现象保留下来，以后这种事物虽未出现，但在一定条件影响下，它的形象仍会在头脑中再现，这就是表象。只有经历过直观的、生动的表象积累，才能深刻地、丰富地认识数的内涵。

一、推算感知，建立大数的表象

在整数的认识中，对于比较小的数，学生可以借助于实物如小棒、方块、计数器等来建立表象；对于以千、万计数的稍大的整数，也可以通过整体感知来建立表象，比如：把一千根吸管扎成一捆有多粗、一千粒黄豆装在玻璃瓶里有多少等，让学生从整体来感知这个数的多少。但对于更大的数，比如几百万、几千万甚至几亿等，由于数量庞大，看不到又摸不着，学生对其表象的建立尤为困难。

推算，可以很好地帮助学生建立对大数量的表象。所谓推算，简单地说，就是“以小博大”，通过小数不断地推算出大数来。

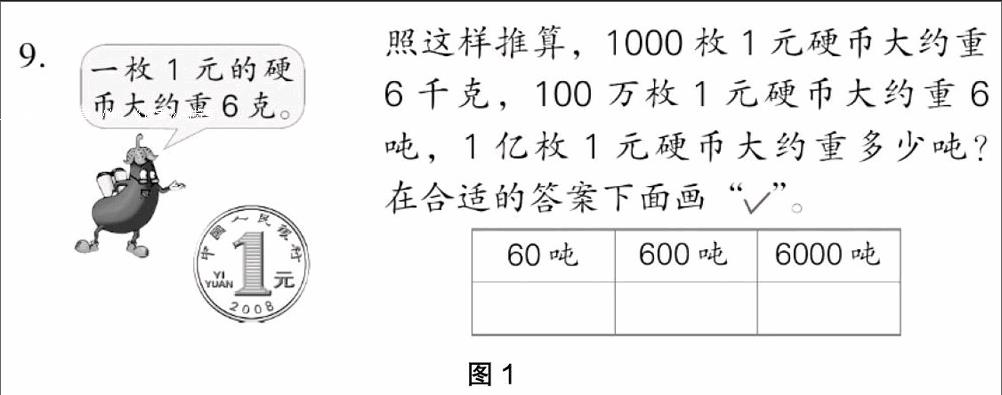
比如，学生认识了计数单位“亿”后，教材中出示了这样的推算问题（如图1）。“1枚硬币”，这是学生可以在手上掂一掂的具体的物体，看得到、摸得着，很形象。但是1000枚、100万枚、1亿枚硬币是一个怎样的概念呢？这里，将硬币的数量和相对应的重量结合，让学生通过对具体重量的感知，来感受其数量之大。

除了和重量相结合，还可以巧妙地和时间、长度、面积等建立联系，通过具体量的推算，来帮助学生建立数的表象。

比如像这样的天文数字：地球赤道6378137米、地球到月球的平均距离384400000米等，这些数学生只知道很大，但到底有多大，学生却很茫然。在下面这个教学片段中，这位老师巧妙地通过绘本《壶中的故事》引出一个天文数字，再将这个天文数字进行一定方式的推算，帮助学生很好地建立了大数的表象。首先，绘本讲述了这样一个美丽的故事：“翻开这本书，一只美丽的壶呈现在眼前。壶中有一座岛，岛上有两个国家，两个国家各有三座山，三座山上各有四个城堡，四个城堡里各有五个村庄，五个村庄里各有六栋房子，六栋房子里各有七间房间，七间房间里各有八个柜子，八个柜子里各有九只箱子，九只箱子里各有10个壶。”到底有多少个壶呢？学生一步一步地算下来，竟然得到了一个很大的数：1×2×3×4×5×6×7×8×9×10=3628800（个）。“3628800”这个数有多大呢？接下来，进行了这样一系列的推算：（1）假如一个壶的宽是1分米，3628800个壶排成一排，有多长呢？有360多千米。如果一辆小汽车在高速公路上每小时行120千米，那么就要行驶3小时。（2）如果1秒钟打开一个壶盖，那么打开所有的壶盖，会花费多长时间？要1000多个小时，40多天。也就是说，揭壶盖的人不吃不喝，也不休息，持续不停地开，也要花一个月以上的时间。通过这样的推算，与现实生活中的时间、路程相结合，学生被震撼了，真真切切地感受到诸如此类天文数字之巨大。

二、形中蕴数，体会小数的结构

小数是十进制分数的一种特殊表现形式。如何帮助学生建立0.1，0.01， 0.001这些小数的计数单位的表象？教材选用的是正方形，最后一个是正方体（如图2）。

教材呈现的图中，将一个正方形平均分成十份，其中的一份就是十分之一，也就是0.1；同样，将一个正方形平均分成一百份，其中的一份就是百分之一，也就是0.01；将一个正方体平均分成一千份，其中的一份就是千分之一，也就是0.001。这里，将小数蕴藏在图形里，用直观的图形来表征小数的意义。

还可以将方格图、方块图和数轴相结合，引导学生从直观到半抽象再到抽象，逐步建立小数的表象。

如图3，将正方体、数轴和小数一一对应，将一个正方体平均分成一百份，其中的一份对应数轴中的“0.01”，其中的两份对应着数轴中的“0.02”，同样，其中的11份对应着数轴中的“0.11”等。這里，给予小数以生动、直观、丰富的表象支撑，在不同的表征形象中，让学生感悟，不管是一个图形，还是一条线段，只要平均分成一百份，其中的一份或几份就是零点零一或零点零几，从而帮助学生丰富小数的内涵。

此外，借助在数轴中找数，还可以帮助学生感受小数的稠密性。比如，在3.14和3.15之间找3.141，学生发现需将其再平均分成十份，取其中的一份，和3.14合起来就是3.141；接着，在3.141和3.142之间找3.1415，同样，将这一部分再平均分成十份，取其中的五份，和3.141合起来就是3.1415；继续这样平均分下去，源源不断，会找出更多的小数。随着平均分的份数越来越多，不可能在图中继续分下去，但在学生的脑海中会不断地涌现，学生从中不但能构建计数单位越来越小的小数，同时深深体会到小数的稠密性。

三、逐步抽象，构建分数的意义

学生对分数意义的构建是逐步推进的，在小学阶段，分成三个阶段来认识分数。第一个阶段在三年级上学期，这时研究的对象是一个物体、一个图形。把一个物体平均分成若干份，表示其中一份或几份的数就是分数。第二个阶段在三年级下学期，这个阶段出现了计量单位和许多物体组成的一个整体。而到了五年级下学期，学生认知的关键则是建立分数的意义。在这个阶段，学生要认识到分数和自然数、小数一样，它是一个数，它本是具有无量纲性的，这与被平均分的对象是没有关系的。在学生的经验里面可能会认为，三分之二的苹果和五分之二的梨是没有办法比较大小的，但是如果建立了无量纲性的概念，学生应该可以体会到，比较三分之二和五分之二的大小，跟它所对应的那个具体的物体是没有关系的，只要直接看三分之二和五分之二本身的意义就可以了。所以，这时的教学重点就应是帮助学生实现从有量纲性向无量纲性的转变。

在下面这个教学片段中，教师通过从具体的实物抽象出有量纲性的分数，再通过对分数外延的理解、扩充，逐步将分数过渡到无量纲性。

课中，在认识了单位“1”之后，围绕3幅图，组织学生来做一个研究。这3幅图分别是：一个饼、四个饼组成的一个整体、5个饼摞起来的一个整体。组织学生探索：（1）分一分，涂色表示每幅图的四分之一；（2）说一说，每幅图分别把什么看作单位“1”？平均分成几份，表示这样的几份？（3）想一想，四分之三表示什么？学生探索、思考、交流后得出，把单位“1”平均分成四份，取其中的三份，就是它的四分之三。但这时，学生对四分之三的认识是有量纲性的，它代表的是四分之三个饼或四分之三个“饼的整体”。在这个基础上，老师提问：九分之四表示什么？十一分之五表示什么？带着自己想说的，我们来进行深入思考：（1）说一个分数，并说说它的含义；（2）想一想：什么样的数叫作分数？分数的分子和分母各表示什么？学生在举例、表述、比较中不断进行思考，将具体的分数之间进行沟通、联系，概括出“把单位“1”平均分成若干份，表示这样的一份或几份的数，叫作分数”，从而实现将分数从有量纲性到无量纲性的过渡。

所以，建立数的表象，是帮助学生深刻认识数的内涵的重要桥梁。只有对数的表征认识清楚、到位，才能在具体、直观的基础之上逐步抽象，最终真正建立起数的概念，丰富数的内涵。endprint