辅助线添加策略的探寻
2017-11-20陈海烽

[摘 要] 本文通过对平面几何中“辅助线的添加”进行探讨,提出“从定义模型中发现辅助线身影,在操作实验中确定辅助线思路,从美学角度寻找辅助线踪影,从平衡理论中寻找辅助线印迹,从大小格局中探寻辅助线踪迹”五种策略.
[关键词] 辅助线;策略;实验;格局
在平面几何教学中,辅助线的添加往往是学生几何学习的“拦路虎”,对优等生来说,也常心有余悸,对中等生来说,更是噩梦一场. 许多学生都有这样的体会:如果题目有辅助线做法的提示,那么问题就会较快得到解决,但如果没有提示,往往会陷入束手无策之中. 一日,徒弟郑巧斌老师(以下简称郑)问我:“陈老师,学生在学习几何时总是很怕做需要添加辅助线的题目,你有什么好的教学策略吗?”这个问题在平面几何教学中确实经常遇到,是一类最常见且迫切需要解决的问题. 虽然辅助线千变万化,但也并非无迹可寻,于是我们有了如下讨论.
从定义模型中发现辅助线身影
陈海烽(以下简称陈):辅助线的添加确实是一个值得我们深入研究的问题,我们一起来梳理一下. 初中阶段是从什么时候开始涉及需要添加辅助线的几何题目的?
郑:应该是从第五章“相交线与平行线”(人教版)就开始的吧!
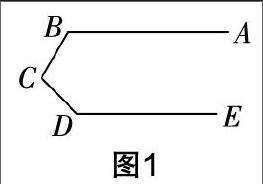
陈:很好,其实在这个章节中,一般老师会遇到如下这道题. 如图1,已知AB∥DE,求证:∠ABC+∠BCD+∠CDE=360°.
郑:对,这道题很典型,但是学生的掌握情况好像不好,如果知道要过点C添加一条辅助线,那么这道题就很简单了.
陈:你认为学生为什么想不到添加辅助线呢?
郑:对结论的把握不清晰. 如果知道两个180°,那么就应该知道要添加辅助线了.
陈:你只讲对了一部分. 其实在教学时需要我们有所“作为”的. 如何刻画两条直线平行,除了我们的外在感官外,还需要有一条直线辅助,才能将位置关系转化为数量关系,这就需要一条截线. 我们现在看到AB∥DE,还看到了一条折线BCD,但这并不是截线,那么我们需要帮助,这个帮助就是我们做辅助线的“念头”.
郑:如果从这个思路或想法入手,就会有很多办法.
陈:是的,至少有如下策略(如图2~4). 当然,如果学生认为BC是一条截线,回到平行线的基本模型,這时就需要过点C作CF∥AB(或CF∥DE),图5也就是你所说的方法,那么自然就水到渠成了.
郑:是不是可以这样理解,我们在讲解定义或模型时要理清模型中的结构,这样可以帮助学生理清模型特征,还原出模型. 《义务教育数学课程标准》修订组组长史宁中说过:“模型的最初建立是基于观察和想象的,而不是基于推理的;判断模型正确与否的标准是基于经验的,而不是基于理性的. ”比如平面直角坐标系中,我们经常添加垂直于两轴的垂线段,这也是基于对坐标本质的理解吧.
陈:总结得很好. 比如我们看到有公共顶点的两条相等线段,其实具备了旋转的部分特征——顶点可以看作旋转中心,两条相等的线段可以看成是由其中一条线段经过旋转而形成的. 这时我们可以考虑将图形进行旋转. 所以,希望我们老师在讲解的时候可以帮助学生理清这个结构模型. 不少老师善于总结解几何题的一些基本图形,这些基本图形就是题目的一个“器官”,教学时我们要多创设情境加以指认和识别,提高学生的审图能力,进而提升他们的核心素养.
在操作实验中确定辅助线思路
陈:我们再来看一道单元测试中的试题. 如图6,在等腰三角形ABC中,AB=AC,∠A=20°,在边AB上取一点D,使AD=BC,求∠BDC的度数.
郑:这是竞赛题呢,这是压轴题!这道题我做过,学生肯定很少做出来,貌似要构造等边三角形,但是如何想到要构造等边三角形的呢?
陈:是的,这也是很多优等生也存在的疑问. 讲解这道题时,我让学生进行了数学实验.
郑:头一回听说数学实验,说具体点.
陈:我让学生量出∠BDC=30°,然后追问学生,如果∠BDC=30°,那么∠ACD应该为多少度?学生都回答10°,接着我再追问学生,在本图中,如何才能得到有个10°的角?学生马上想到作∠A的平分线. 我又继续追问,这样一来,我们能否找到一个和△ADC全等的图形?需要多少度的角?学生回答需要有20°的角,这时让学生自己探索,就有不少同学发现以BC为边作等边三角形后,就会出现一个含20°角的三角形,从而问题就容易解决了. 如图7,以BC为边作等边三角形OBC,易证△ABO≌△ACO,接着证明△ACD≌△CAO,就可以得出答案了.
郑:您这样让学生实验操作,学生就很容易从这些条件中找到答案,而且学生经历了操作确认的过程,能完成逻辑证明. 记得《义务教育数学课程标准》就指出:“学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理验证的过程. ”数学实验正好契合新课程理念,有利于提升学生的核心素养.
陈:没错,我们在教学时要让学生学会数学实验,当然也包括思维实验,我们现在最流行的数学软件——几何画板也可以用来探寻作辅助线的思路. 在精确作图的基础上,借助最常用的三角板、量角器等数学学具,可以帮助我们发现一些靠谱的结论,这就等于把握了解题的方向,使我们的解题不至于像无头苍蝇. 这里要特别说明的是,对于一些较难的压轴题,虽然题目中已经配上了图形,但是学生看到的只是成品,并没有看到这个图形的生长过程,所以建议在教学时务必让学生感受这个过程,让学生知道这个图形是如何生长出来的,同时通过这个过程,感悟图形要素(或元素)之间的从属关系,进而在确定图形的过程中生长出作辅助线的念头.
从美学角度寻找辅助线踪影
陈:我们还可以从美学特征中寻找辅助线踪影.
郑:美指的是那些简洁美、对称美、和谐美、奇异美吗?endprint
陈:是的,其中对称美对我们添加辅助线帮助最大. 拿我们最常见的角平分线来说,通过它,我们能将这个角进行翻折,或者说角是一个轴对称图形,角平分线所在的直线就是它的对称轴. 如果能从这个角度就可以找到解题思路.
郑:比如下面这道题. 如图8,AD平分∠BAC,∠B+∠C=180°,求证:DB=DC.
陈:这个题目很典型,如果学生知道角平分线是一条美学中心线,利用美学思想,可以有如下几种作法(如图9~11).
郑:从美学角度,相信学生能更好地理解辅助线作法的由来,也可以知道这三种辅助线作法本质上是一致的,对一题多解就更加容易接受了. 我觉得很多翻折、平移、旋转其实也是一种广义的对称,也都具有美学的特征.
陈:没错. 教学时我们应该多从美学的角度阐释数学知识,比如教学垂径定理时,可以让学生通过折叠圆的方法,充分利用其对称美来研究问题,这样,学生对定理的认识就会有新的高度. 再如,直线与圆的位置关系,也可以通过对称美折叠圆的方法发现很多性质. 经过这样的引导教学,学生更容易明白为什么要作弦心距这条辅助线,为什么见到切线要连半径得到垂直.
从平衡理论中寻找辅助线印迹
陈:此外,我们还可以从平衡理论中找寻辅助线印迹. 比如我们常见的截长补短就是一种很好的平衡理论的应用. 如要证明“a=b+c”,常用的策略就是从a中分成两段相加,即a=b1+c1,即先让b=b1,然后证明c=c1,这样,式子的两边就都是两两相加的结构,两边都平衡了,达到了证明的目的. 当然,我们也可以将“b+c”通过辅助线将其延长,补成一条线段a,从而完成证明,这是很明显的应用之一. 学生明白了这些,就会更容易理解截长补短的本质. 当然,类似的还有如下试题. 如图12,已知点E,F分别在正方形ABCD的边BC,CD上,分别连接AE,AF和EF,若∠EAF=45°,试说明EF=BE+DF.
郑:你的意思是∠EAF=45°占了∠DAB的一半,另外两个角,即∠EAB和∠DAF的和也是45°,我们要将两者拼在一起才能平衡,所以想到作辅助线,将图形△ADF进行旋转,是吗?
陈:没错,这样的话,学生的理解会更顺一些.
郑:是的,实际上,总有很多学生想将EF截成两段,或者过点A作EF的垂線段. 如果能从平衡中入手,就不会再纠结了.
陈:对. 因此,在教学中,遇到线段或角的和、差、倍、分问题,要引导学生从结论出发,利用平衡理论原理,让学生体会将结论逐步转化的过程,即从不平衡的状态通过恰当的辅助线达到平衡的状态.
从大小格局中探寻辅助线踪迹
陈:另外,我们还可以从大小格局中寻找辅助线踪迹. 比如,我们看到一个有关中点的题目,我们会提醒学生展开联想.
郑:就是联想倍长中线,三线合一,直角三角形中斜边上的中线等于斜边的一半,中位线定理等.
陈:说得好,譬如倍长中线,还有不少老师总结“倍长中线找倒8”,也就是找个“8”字形的结构,然后让学生证明全等.
郑:对呀,这有什么问题吗?
陈:当然没什么问题,但是我们可以引导学生从更大的格局来看待问题. 倍长中线后,除了两个全等的三角形外,我们其实还可以看到一个平行四边形,让学生连接成平行四边形后,需要通过全等获得的条件可以直接从平行四边形中获取,解题的书写长度更短.
郑:学生老是用全等,看来可以再稍做改进. 我们在平面直角坐标系中,经常让学生补成矩形或梯形,将三角形的问题看作是它们的一部分,是不是可以看作是这种策略的运用?
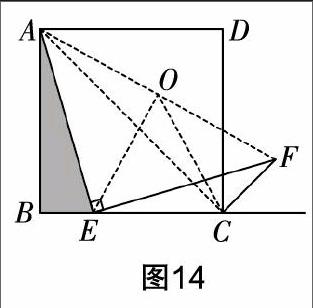
陈:是的. 当然,我们在教学时要注意对课本知识进行再探究. 比如下面这道题. 如图13,四边形ABCD是正方形,E为BC上一个动点,∠AEF=90°,且EF交正方形ABCD的外角平分线CF于点F,求证:AE=FE.
陈:这道题是我们在八年级下册学习“正方形”后的一道课后习题,课本还给出了相应的提示. 我们在初三教学四点共圆的条件时再让学生做这道题,发现了双直角模型,存在的一个更大的格局是A,E,C,F四点共圆,于是添加如下辅助线证明更为快捷. 如图14,连接AC,AF,取AF的中点O,连接OE,OC,则AO=EO=CO=FO. 所以A,E,C,F四点共圆. 所以∠AFE=∠ACE=45°. 所以△AEF是等腰直角三角形. 所以AE=FE.
郑:哦,我知道了,比如将四边形的问题转化为三角形问题,再将一般三角形问题转化为特殊的直角三角形问题,就是从小格局上入手. 若把斜三角形放在一个大矩形或一个平行四边形中,就是从大格局上考虑. 教学时,我们要让学生感悟事物之间是普遍联系的这一哲理,让学生知道一个图形不是孤立的,可以前后关联在一起,形成一个更加良好、系统的格局.
陈:是的,这样的例子相当多,对学生来说也比较容易想到. 教学时,要提醒学生辅助线的功能就是将分散的条件集中起来,将隐含的条件显现出来. 另外,作辅助线一般要遵循一个原则,即“不可贪,不可破”!其中“贪”的情况比较普遍,比如学生经常在作辅助线时说这条辅助线不仅能和谁垂直还要和谁相等,这显然就是贪多了,再如本文开头的第一道题,假如作平行线CF∥AB且CF∥DE,显然不妥. “不可破”就是作辅助线时尽量不要破坏已知条件,不能通过辅助线得了一个条件,反而失去一个可用的条件,这样反而得不偿失了.
郑:这个本质和原则今后我会加强渗透,总结你讲的上述策略,我发现也很有美感. 一,从定义模型里寻找辅助线身影;二,从实验操作上寻觅辅助线思路;三,从美学特征中发现辅助线踪影;四,从平衡理论里寻找辅助线印迹;五,从大小格局中寻找辅助线踪迹. 今后,在执教中引导学生通过解题慢慢领悟,就能不断地提高他们的数学素养,那么学生对需要添加辅助线的题目就会更有信心.endprint
