一类生物趋向性运动建模及其算法的研究
2017-11-20唐东成张晓亚李欣雪
唐东成,张晓亚,李欣雪
(广东理工学院 电气工程系,广东 肇庆 526000)
一类生物趋向性运动建模及其算法的研究
唐东成,张晓亚,李欣雪
(广东理工学院 电气工程系,广东 肇庆526000)
根据生物界生物对环境“趋利避害,适者生存”的普遍规律,建立了生物在环境刺激的因素下产生的趋向性运动的数学模型。然后利用该模型模拟生物个体在二维空间中的运动,以此验证该模型的合理性,并提出一种生物趋向性算法(BiologyTendencyAlgorithm,BTA)。数值仿真结果表明了生物趋向性算法解决优化问题的有效性。
趋向性;生物趋向性算法;优化
0 引言
受大自然现象和运动规律的启发,众多学者开展启发式算法的研究,并得到了丰硕的成果。目前较为常见的启发式搜索有粒子群算法[1]、人工鱼群算法[2]、遗传算法[3]、萤火虫算法[4-5]、模拟退火算法[6-7]、蚁群算法[8-9]等。与经典的数学算法不同,启发式搜索算法能很好地解决复杂的非线性的优化计算问题,因此,这些算法在各个领域中得到了广泛应用,成功解决了工程中涉及的许多问题,如工程设计与优化领域、电力系统领域、机器人控制领域、交通运输领域、通信领域、计算机领域等。
生物个体在实际生存环境中,往往会受到外界的“激励”作用,而发生某一特定的生物行为运动(如生物的趋光性、趋热性等),以适应生物个体的生存环境。受到生物这一行为的启发,本文提出一种生物趋向性算法(Biology Tendency Algorithm,BTA)。首先建立生物在环境刺激下的趋向性运动的数学模型。然后利用该模型模拟了生物在二维空间内的运动情况,验证了该模型的合理性。最后,对所提出BTA算法进行数值仿真,实验结果表明生物趋向性算法解决优化问题的有效性。
1 生物趋向性运动的建模及仿真
1.1生物趋向性运动模型建立
假设存在某一空间,在该空间中生物的生存环境条件(“激励”因素)与不同的空间位置有关,即生物所在空间的环境条件G按空间位置进行分布。空间位置X∈Rn,则环境条件的分布满足:
G=f(X)
(1)
于是对于某一个生物个体Ii来说,它所处的空间位置为Xi,而在该位置该个体所处的环境条件为Gi;同时考虑该个体对环境都有一定的适应能力,并且该适应能力与环境条件有关;即使在同一位置不同生物个体的适应能力也会有一定的差异。因此,在此给出了体现生物适应能力的公式,即:
Mi=Ke(f(Gi)-Ci)
(2)
式(2)中,Mi表示生物个体Ii的适应能力,K为适应能力系数,Ci表示生物个体Ii对环境刺激的适应程度的一个参量,该值越大,则生物个体对环境的适应能力越差,因此,生物个体在环境中的适应能力就越弱;反之,该值越小,则说明生物个体在该环境中适应能力越强。
在外界环境作用下,生物个体出于本能,它会朝着有利于它生存的空间运动,一般生物个体会朝着环境因素最佳的位置运动,每个生物个体在局部空间范围内随机地运动。个体随机运动到某个空间位置时,个体在某个位置的适应能力会变化,并且在局部范围内个体朝着适应能力最强的位置运动。
如果空间中存在多个生物个体,每个生物个体间可以通过一种信息交换的方式相互告知各自所处的环境条件,那么他们就可以朝着环境最佳的地方前进。但是生物个体之间存在一定的差异,它们在相应环境中的生存能力是不同的,这样就造成某些个体即使在较好的环境中,它的适应能力不够,因此该生物个体的活跃程度不够,所以该个体的运动速度减弱。考虑到生物个体运动速度与适应能力有关,在这里给出个体的速度公式为:
(3)

图2 不同K值时生物个体的趋性运动图

(4)
1.2模型数值仿真
为了验证该模型的正确性,假设生物个体均处于某一限定的二维空间内,X∈R2,且在空间中环境条件的分布为:

(5)
式(5)中,生物个体Ii的坐标为(xi,yi);为了将衡量环境条件的取值限定在[0 1]范围内,对Gi进行如下处理:

(6)
Gmin、Gmax分别为空间中所有生物个体生存环境条件最差值和最佳值。此时,个体的适应能力Mi的公式变为:
Mi=Ke(gi-Ci)
(7)
式(7)中,Ci为[0,1]范围内的随机值,以此参数体现个体对环境的差异性。结合式(3)、式(4)建立生物趋向性运动模型。
已知式(5)的环境条件分布的最佳位置为(0,0),给定5个生物个体,它们的初始位置依次为(0,5)、(4.755 3,1.545 1)、(2.938 9,-4.045 1)、(-2.938 9,-4.045 1)、(-4.755 3,1.545 1)。并且个体运动的最大时间为T=100,系数K=0.1。在仿真中,5个生物个体会趋近于环境条件最佳位置(0,0),如图1所示。

图1 生物个体在二维空间内的趋性运动
为了研究适应能力系数K的值对生物趋性运动的影响,此处给出不同K的取值时的仿真效果和仿真数据。如图2和表1所示。

表1 不同K值所对应的x2+y2的最小取值
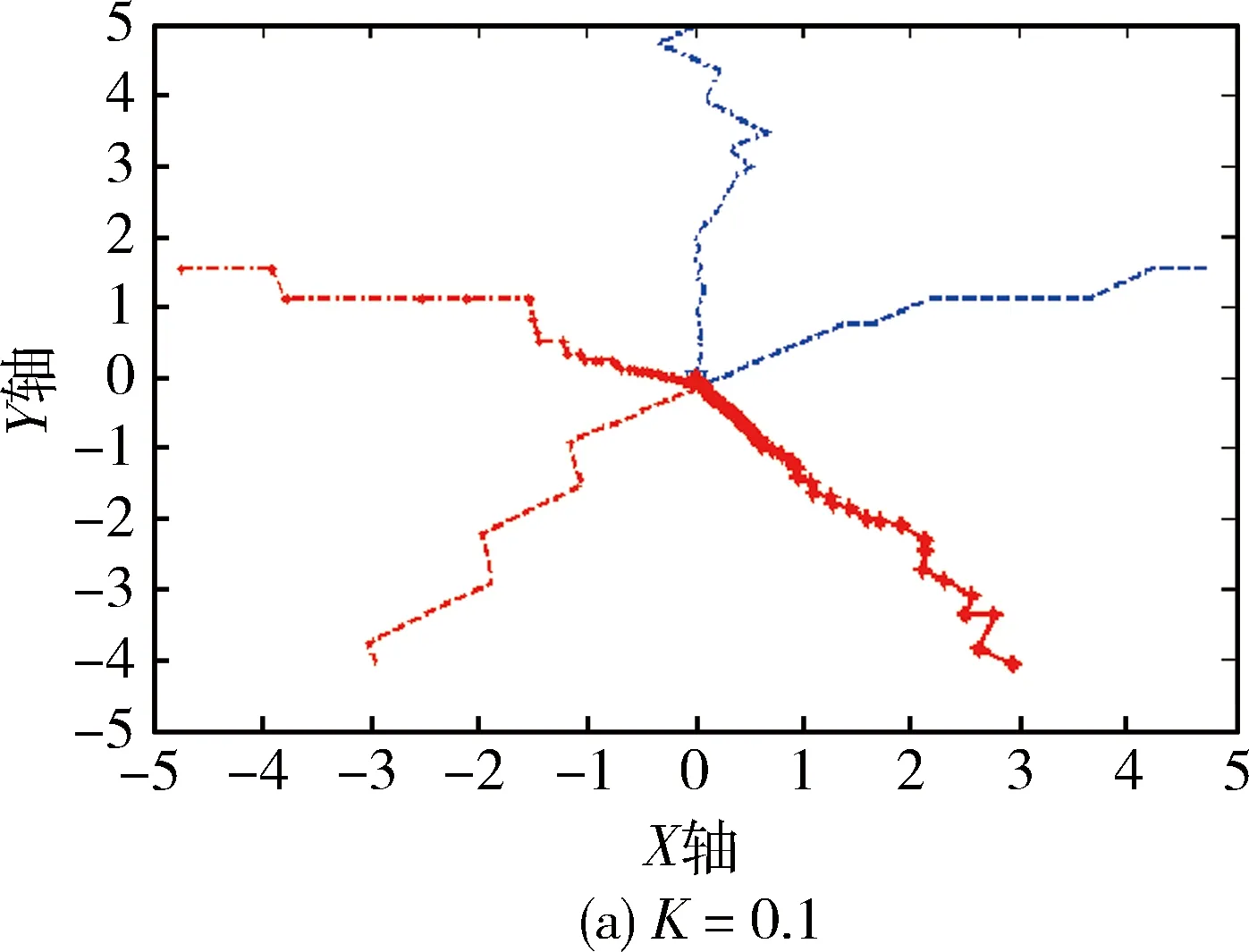
从仿真数据来看,随着K值的增大,求取x2+y2的最小取值的数量级也增大,这表明K值与运动的收敛性有关,或者说适应能力M对收敛性有很大的影响。研究发现M的值不易过大,过大会导致局部收敛;也不宜过小,过小则会出现收敛速度慢,并且在生物的生命周期内无法到达最佳环境位置。K取值在(0.1,0.5)范围内均有较好的收敛效果。
2 生物趋性运动算法
由此生物趋性运动模型,提出一种生物趋性运动的算法,算法步骤如下:
(1)在空间随机产生N个生物个体Ii,初始化迭代次数T;


(4)根据式(3)、(4)更新生物个体的速度和位置;
(5)当迭代次数满足要求,则获取处于最佳环境的生物个体的位置作为最优解;否则转移到步骤(2)。
3 仿真实验
本文在Windows 7系统下使用MATLAB 2011b软件进行仿真实验,并采用了5个经典测试函数来验证算法的有效性,在此算法中先设置了初始参数,K=0.3,Ci为[0,1]之间的随机值,迭代次数T=1 000,生物个体总数量N=30。其中所选的测试函数如表2所示。

表2 测试函数
在表2中,f1为Sphere单峰二次函数,主要用来测试算法寻优精度;f2为Rosenbrock函数,是一个非凸、病态函数;f3为Rsatrigin多峰函数,存在10n个局部极小点,一般算法难以得到全局最优解;f4为Ackley函数,是一个具有深度局部最小点的多峰函数;f5是Griewank函数,多峰,存在大量局部极小点[10]。f3~f5主要用来检验算法全局搜索性能和避免早熟。利用该算法对测试函数进行求解,求取了不同函数的结果值,并通过多次测试得到最优解平均值,如表3所示。不同测试函数的进化曲线,如图3所示。该算法的寻优精度达到10-4数量级,且容易出现早熟,全局寻优能力较差。

表3 结果平均值

图3 不同测试函数的进化曲线
4 结束语
本文从生物趋向性运动角度出发,总结其趋向性运动的一般规律,提出了BTA算法。就算法本身来说也属于一种启发式算法。从数值仿真情况来看,该算法具有一定的有效性。但算法的收敛速度、寻优精度,以及全局寻优能力还有待进一步提高。
[1] KENNEDY J,EBEHARTR C.Particle swarm optimization[C].Proceedings of IEEE International Conference on Neural Networks.Perth: IEEE Piscataway,1995:1942-1948.
[2] 李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式:鱼群算法[J].系统工程理论与实践,2002,22(11):32-38.
[3] HOLLAND J.Adaptation in natural and artificial systems[M].Ann Arbor,MI: University of Michigan Press,1975.
[4] KRISHNAN K N,GHOSE D.Detection of multiple source locations using a glowworm metaphor with applications to collective robotics[C].Proc.of Swarm Intelligence Symposium.IEEE Press,2005:84-91.
[5] 王沈娟,高晓智.萤火虫算法研究综述[J].微型机与应用,2015,34(8): 8-11.
[6] METROPOLIS N,ROSENBLUTH A,ROSENBLUTH M.Equation of state calculations by fast computing machines[J].Journal of Chemical Physics,1953,21:1087-1092.
[7] 吴意乐,何庆.基于改进遗传模拟退火算法的WSN路径优化算法[J].计算机应用研究,2016,33(10):2959-2962.
[8] DORIGO M,MANIEZZO V,COLORNI A.Theantsystem: an autocatalytic optimizing process technical report 91-016[R].Milan,Italy: Dipartimento di Elettronica,Politecnico di Milano,1991.
[9] 黄翰,郝志峰,吴春国,等.蚁群算法的收敛速度分析[J].计算机学报,2007,30(8): 1344-1353.
[10] 周少武,陈微,唐东成.基于亲和度的改进引力搜索算法[J].计算机工程,2014,40(8):201-204.
Research on modeling and algorithm of a kind of biological trend
Tang Dongcheng,Zhang Xiaoya,Li Xinxue
(Department of Electrical Engineering,Guangdong Polytechnic College,Zhaoqing 526000,China)
According to the general law “profit and avoid harm,survival of the fittest” in the biology world,the model of the biology tendency movement was established under the environmental stimulus.Then the model was used to simulate the movement of biological individuals in two-dimensional space,and the rationality of the model was verified.And a biological tendency algorithm (BTA) was proposed.The numerical simulation results show that the bio-trend algorithm is effective in solving the optimization problem.
tendency; Biological Tendency Algorithm (BTA); optimization
TP301.6
A
10.19358/j.issn.1674-7720.2017.21.006
唐东成,张晓亚,李欣雪.一类生物趋向性运动建模及其算法的研究J.微型机与应用,2017,36(21):19-21,25.
2017-05-02)
唐东成(1987-),男,硕士,主要研究方向:复杂系统分析与控制。
张晓亚(1987-),女,硕士,主要研究方向:工业故障诊断。
李欣雪(1990-),女,硕士,主要研究方向:电子与通信工程。
