基于CFD方法对摆线推进器水动力性能的数值预报
2017-11-20刘浩然杨玉良闫永思
刘浩然, 杨玉良, 闫永思
(上海船舶工艺研究所, 上海 200032)
基于CFD方法对摆线推进器水动力性能的数值预报
刘浩然, 杨玉良, 闫永思
(上海船舶工艺研究所, 上海 200032)
通过运用CATIA建模软件、ICEM CFD网格划分软件及FLUENT求解器分别对摆线推进器进行几何模型的建立、网格划分及数值计算,进而选用合适的湍流求解方法及滑移网格方法得到与试验值相近的数值模拟结果,从而验证该方法的可靠性。
CFD;摆线推进器;滑移网格;湍流模型
1 CFD技术模拟摆线推进器可靠性验证
由于目前关于摆线推进器的试验参考资料较少,理论方法以朱典明[1]的《摆线推进器理论计算方法》为基础,该文中的试验值及理论计算值作为验证本文关于计算流体力学(Computational Fluid Dynamic, CFD)技术模拟求解摆线推进器水动力性能结果的依据,为保证结果的准确性,摆线推进器各尺寸以该文中的几何模型参数为参考[2]。
2 摆线推进器模型参数及几何模型的建立
CATIA软件是法国Dassault System公司旗下的CAD/CAE/CAM一体化软件,最初源于航空领域,但其功能覆盖了曲面、实体、零件加工、机构分析和动画制作等各个方面。通过CATIA软件设计出的产品,在质量上得到验证之后,该软件逐渐过渡到其他一些领域,如船舶领域[3]等。目前,在船舶制造领域,已经开始使用该软件。主要应用于一些流体计算模型,由于CATIA软件在曲面设计方面有较大优势,因此在对船体的型线进行三维建模时,可以提高船舶设计过程的效率和最终模型的质量。本文所涉及桨与船体的几何模型均由CATIA软件建立。
为合理验证该计算方法的可靠性,选用与试验中几何模型相似参数翼型NACA 3412,tm(叶厚最大值) 相对厚度位于30.9%翼弦处,Sm(最大弯度)相对弯度位于40.2%翼弦处,如图1所示。同理,为与试验提供的几何参数相近,叶片选用矩形轮廓,即在纵向上保持截面不变。叶片的旋转中心在弦长的40%处[4]。表1和表2分别为试验参数模型尺寸与本文计算模型尺寸。由于叶片附近的流场信息比较关键,因此叶片的计算域划分尽量小一些,并且网格密度相对大一些。

图1 NACA 3412翼型

表1 摆线推进器模型主要参数

表2 摆线推进器计算几何模型参数
根据设定好的尺寸,用CATIA软件对其进行建模,如图2所示。

图2 摆线推进器几何模型
3 各计算域网格划分
选用ICEM CFD软件进行网格划分。根据几何模型的特点及推进器叶片的运动情况可知,各叶片附近网格应保持相同,为减少人为因素对其求得结果的影响,在对单独桨叶划分完成后,以此为基础进行旋转并复制,完成其余叶片计算域的划分。考虑到叶片计算域几何模型相对规则,选用结构化网格进行划分,可提高计算效率且节省计算资源。首先,创建一个单独三维块将整个叶片包含在内,然后对块进行近似贴体网格的切分,对于叶片各块中节点的分布,以叶根处与叶梢处为对应关系,可以有效预防或减少畸形网格数量。由于在翼型的尾端通常会有一个尖角,通过修补功能将其变为一个曲率连续的圆弧,在选定块中进行单独的切分,以满足网格质量的要求。又由于翼型为圆弧状,因此对其进行外O型切分,通过块的坍塌合并掉不必要的映射块,从而减少不必要的网格数量,这样可防止出现趋于0°角与180°角的情况,从而合理地将各网格单元角度控制在较优质量上。叶片网格附近区域的第1层网格厚度根据Y+值进行设定,最终确定边界层数为5层,第1层为0.1 mm,缩放因子设为1.1向外延伸,在边界层之后的网格缩放因子设置为1.2,以保证网格的平滑过渡。最终生成的网格数为7.2×104,如图3所示。

图3 叶片网格划分
推进器计算域网格主要以非结构网格形式进行划分,因为在其内部有6个叶片计算域所产生的空心圆柱部分,所以在类似这种几何模型不规则的情况下,选用非结构网格比较合适。根据非结构网格划分方法,先进行全局网格尺寸设置,scale factor设定为2,而max element设定为8,此处应设为2的整数次幂,因为后台运行计算是以2的整数次幂进行计算的,否则在网格生成时,会将非2的整数次幂的数圆整到最接近2的幂,从而影响网格划分的质量。在全局设置后,通过Part网格设置,对与叶片计算域相交的interface面处进行网格加密,以保证网格之间在进行数据交换时正常运行。最终推进器非结构化网格单元数为30.3×104,如图4所示。

图4 推进器计算域非结构化网格
推进器计算域外流场以结构网格划分,对中间的推进器所产生的空心大圆柱应用外O型切分,并且将几何模型中的圆形轮廓投影到整个计算域的底部,以便更好地完成网格各节点的映射,进而避免由于单元节点的分布不均而产生扭曲网格的问题。网格数为35.6×104,如图5所示。

图5 推进器内外流场计算域网格划分
4 边界条件及湍流方法的设定
摆线推进器的数值模拟,其边界条件设置为4个部分,分别为流体的速度入口,压力自由流出,交接面和壁面。由于本文不考虑空泡,速度入口即为来流速度,压力均设置为0,壁面为不可穿透且光滑,远流场为自由流出,即流体自由穿过,如图6所示。

图6 边界条件设置
根据上文对各湍流方法的叙述,湍流求解方法选用RNGk-ε模型并使用增强壁面函数,压力与速度的耦合方式选用半隐式方法,即SIMPLE算法。压力插值方式为PRESTO!。动量、湍动比和湍黏比等数值离散方式采用二阶迎风格式。
5 模拟结果及可靠性验证
为使得模拟结果具有可靠性,计算偏心率e分别为0.4,0.6和0.8时,在不同进速系数下摆线推进器的水动力性能。经过一系列的模型建立、网格划分和选用FLUENT求解器进行计算,最终将求得的数值结果与NSRDC试验值进行比较,从而验证该方法的可靠性。分别将计算得到的水动力各项系数在不同速度时的变化情况进行整理分析。
在偏心率e分别为0.4,0.6和0.8时,随着进速系数J的变化得到摆线推进器推力系数KT变化情况如图7所示。推力系数公式为
式中:KT为推力系数;T为推力;ρ为水的密度;n为摆线推进器转速;D为推进器直径;b为叶长。

图7 主推进力系数KT变化曲线
由图7可知,在同一偏心率下,推力系数KT随着进速系数J的增大不断减小,当进速系数J增加到一定值后,会导致推力系数KT减为零。随着偏心率e的变大,其推力系数KT也随之增加且增幅较大,因此在变化偏心率时会使得桨对船舶的推力产生较大的变化。由此可知,在船上使用可调偏心率的摆线推进器时,只要适当改变偏心点位置即可以达到对推力方向及大小的控制,从而突显出其良好的操纵性能。
将模拟结果与试验值比较后可得,该方法所得数值均偏大,这是由于叶片在截面上与试验中桨的截面不同所导致,因此结果会略有增加。在偏心率e为0.4时,出现最大误差为8.8%,但整体模拟效果较好。
在偏心率e分别为0.4,0.6和0.8时,随着进速系数J的变化得到摆线推进器转矩系数KQ变化情况如图8所示。转矩系数公式为
式中:KQ为转矩系数;Q为转矩;ρ为水的密度;n为摆线推进器转速;D为推进器直径;b为叶长。

图8 转矩系数KQ变化曲线
由图8可知:在不同偏心率e时,转矩系数KQ随着进速系数J的增大而减小;相同进速系数时,转矩系数KQ随着偏心率e增大而增大。其变化趋势同推力系数KT类似。
在偏心率e分别为0.4,0.6和0.8时,随着进速系数J的变化得到推进器效率η变化情况如图9所示。推进器效率公式为
式中:η为推进器效率;π为圆围率。
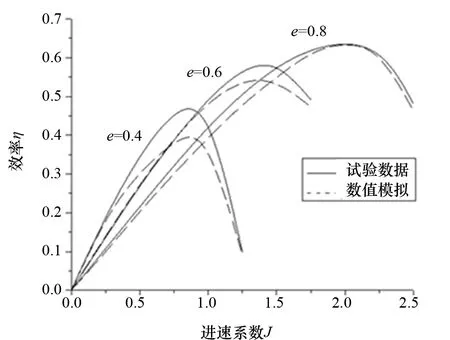
图9 推进器效率变化曲线
从图9可知,推进器的效率先随进速系数增大到一定峰值后再减小,峰值的变化随偏心率及速度系数的增大而增大。当进速系数J较小时,偏心率e较小的效率增长率越大,但是其峰值随偏心率e的增加而变大,当偏心率e增加到一定值时其效率的增长幅度变缓。
摆线推进器在偏心率e为0.6时,各叶片瞬态推力变化曲线如图10所示。在工作一定时间后,摆线推进器的运动达到稳定状态并呈周期运动,因为各叶片之间初始相位差的存在,所以各个瞬态变化曲线仅相差一个相位,又由于6个桨叶均匀布置则相位角为60°。由于该推进器的运动规律,可知其推力变化与其叶片自身旋转有很大关系,在运动时由于各叶片攻角的变化,从而使得推力产生波动。

图10 e=0.6时各叶片瞬态推力变化曲线
摆线推进器在偏心率e为0.6时,各叶片瞬态转矩变化曲线如图11所示,其变化趋势与推力瞬态变化相似,相位差为60°。

图11 e=0.6时各叶片转矩瞬态变化曲线
叶片推力及转矩瞬态变化曲线随进速系数的变化关系如图12所示。当且仅当进速不同时,各叶片运动稳定后其波动的趋势大致相同,但其幅值均有变化。当进速较大时,由于水流对桨的影响较大,因此产生的推力及转矩相对较小,但变化趋势依然相似。从图12可知,最大峰值相对于最小波谷变化更为剧烈,这也是当船舶快速行驶时引起船舶振动的原因之一,因此减小波动幅度对桨减小振动十分有利。

图12 叶片瞬态时随进速系数J的变化情况
通过与试验值的比较可知,各水动力性能系数变化趋势正确,并且误差在可接受范围内,因此应用此方法具有可靠性。
6 结论
本文验证了用CFD技术和滑移网格方法对摆线推进器计算的准确度,通过比较摆线推进器的水动力性能,其模拟结果表明,所选用的方法合理并可靠,为今后关于摆线推进器水动力性能的研究奠定基础。
[1] 朱典明.摆线推进器的理论计算方法[J].哈尔滨船舶工程学院学报,1982(1):24.
[2] 张洪雨.摆线推进器水动力性能研究[D].哈尔滨:哈尔滨工程大学,1999.
[3] 周志勇.CFD在船型优化中的应用[J].船舶设计通讯,2005(2).
[4] 张洪雨,邢国英.摆线推进器任意方向角的水动力计算方法研究[J].水动力学研究与进展,2005,20(4): 472-478.
NumericalPredictionofHydrodynamicPerformanceofCycloidalPropellersBasedonCFDMethod
LIU Haoran, YANG Yuliang, YAN Yongsi
(Shanghai Shipbuilding Technology Research Institute, Shanghai 200032, China)
By CATIA modeling software, ICEM CFD software and FLUENT slover, the geometric model of the cycloidal propeller is established, and the meshing and numerical calculation are completed respectively. The appropriate turbulence solving and sliding mesh methods are used to obtain the simulation results which are similar to the test results, and the reliability of the method is verified.
CFD; cycloidal propeller; sliding mesh; turbulence model
刘浩然(1984-),男,工程师,研究领域为船舶与海洋结构物制造技术
1000-3878(2017)05-0022-07
U661
A
