舰船动态散射回波建模与稳定性分析*

于新源，许波，熊坤，杜海

(1.北京机电工程总体设计部，北京 100854；2.中国航天科工 二院，北京 100854； 3.中国航天科工集团 运载技术研究院，北京 102308；4.北京遥感设备研究所，北京 100854)

☞仿真技术

舰船动态散射回波建模与稳定性分析*

于新源1,2，许波3，熊坤4，杜海4

(1.北京机电工程总体设计部，北京 100854；2.中国航天科工 二院，北京 100854； 3.中国航天科工集团 运载技术研究院，北京 102308；4.北京遥感设备研究所，北京 100854)

研究舰船在动态条件下的散射特性对于目标识别而言具有重要的价值。以“提康德罗加”级巡洋舰为例，首先简要介绍了舰船静态散射特性数据的获取方法，其次以切片理论为核心建立了完整的水动力学模型，进而对舰船的动态散射回波进行了仿真。最后对仿真数据进行了统计分析，获取了舰船在不同海况、不同入射余角条件下的回波稳定性估计，并通过与外场实测数据的比较间接验证了模型的可信性。研究结果可为海面雷达目标识别提供一定的理论支撑。

舰船；静态；切片理论；动态；散射；回波稳定性

0 引言

随着现代复杂战场环境中电子对抗的不断升级，对于舰船而言，仅掌握其静态散射特性已远远无法满足目标识别的需求，开展舰船动态散射特性的研究变得愈加紧迫和重要。所谓的“动态”包含2方面的含义：一是在海浪和螺旋桨等的外力作用下，舰船本身的位置和姿态是时变的；二是在探测平台运动的影响下，雷达波到舰船的照射角度也是时变的，二者共同导致了舰船目标的散射回波是动态的，且具有独特的统计特性。

目前虽已出现部分关于舰船动态散射回波的建模研究[1-3]，但都存在一些问题：文献[1]仅考虑了舰船目标的姿态变化，并没有考虑探测平台运动引起的照射角度的变化；文献[2]将舰船的姿态运动用正弦函数作简化处理，与实际情况差别较大；文献[3]综合考虑了时变海面的散射以及舰船与海面间的多径散射，同时使用了较为完整的舰船水动力学模型，但在对动态散射回波进行验模的过程中仅分析了其时频特性，并未分析其统计特性，且外场实测数据来源于浮标球而非舰船，支撑性较弱。

本文在已有舰船静态散射特性数据的基础上，以较为完整的水动力学模型为依托，在仿真条件下获取了不同海况、不同照射角度下的舰船动态散射回波。通过与舰船的外场实测数据进行比较，二者的稳定特性相符，从而证明了本文的建模方法是可信的。

1 静态散射特性

本文将目标舰船选定为“提康德罗加”级巡洋舰，所采用的静态散射特性数据为一维距离像格式，每个距离分辨单元给出一个RCS值。照射角度范围为入射余角0°～90°，方位角0°～360°。以下分别从几何建模和电磁散射建模2方面对其建模过程进行简要介绍。

在进行几何建模的过程中，首先，对巡洋舰的组件级或单元级外形结构进行剖分形成若干剖面，并在每个剖面上根据外形结构的特点确定若干形值点；然后，依照巡洋舰的特定结构把拆解的组件及其单元搭建成整舰，由组件及单元上形值点数据的总和形成巡洋舰几何模型的剖面数据，从而实现了巡洋舰几何外形的数字化；最后，对组件级或单元级外形结构进行曲面拟合，并在目标几何外形表面上进行网格划分，形成网格的几何模型。图1给出的是采用OpenGL技术，结合特定光照模型得到的巡洋舰实体造型。

图1 “提康德罗加”级巡洋舰实体造型Fig.1 Solid modeling of Ticonderoga-class cruiser

在进行电磁散射建模的过程中，对于巡洋舰的表面散射采用面元法求解，即应用物理光学理论对网格模型中的三角形或四边形面元的表面电流感应场进行物理光学积分而求得散射场；对于巡洋舰上凸凹部分的多次散射采用部件法求解，即含有诸如两面角、三面角、开底腔的部件，在径向任意位置上雷达分辨单元内目标的总散射场经遮挡计算和分辨因子计算后，将上述部件的散射场进行矢量叠加求得。

2 水动力学特性

目前获取舰船水动力学特性的方法主要包括船模试验法、CFD法、理论计算法3种。船模试验法常作为后2种方法的验证手段，具有较高的可靠性，但试验通常需要大量人力、物力、财力的投入，除有条件的单位外，一般研究人员很难采用该方法进行水动力学研究[4]；CFD法在船舶领域的应用目前在理论方面已较为成熟，其计算精度虽然较高，但其计算效率对硬件资源的要求也非常高，另外国内船舶CFD软件的商业化进程较国外还有很大差距，这也大大限制了该方法在工程领域中的推广[5]。

理论计算法经历了从二维理论到三维理论，从线性理论到非线性理论的发展[6]。一方面，三维理论的计算过程十分复杂和费时，且计算精度并未较二维理论有明显提高[7]；另一方面，非线性理论还局限于考虑部分因素，结果比较分散[8]，因此二维线性理论仍然是目前最重要的理论计算方法，不仅计算简便，而且与船模试验有较好的符合程度。狭义上，二维线性理论即指切片理论，包括“原始切片理论”以及后来出现的“新切片理论”[9]。

本文对于水动力学建模的精度要求适中，同时出于节约研究成本的考虑，选用新切片理论对“提康德罗加”级巡洋舰的水动力学特性进行建模。

2.1切片理论

切片理论实质上是一种近似方法，它充分利用船体细长的这一特点，将船体沿船长方向切分为一系列片体，并把每个片体当成截面不变的柱体，这样每个片体的流场都是二维的。将二维流场求解得到的作用力沿船长方向进行积分便得到船体所受的总的水动力。

如图2所示，应用切片理论研究舰船的水动力学特性包括4个步骤，即生成随机海浪，计算水动力系数，计算扰动力和扰动力矩，以及求解舰船的6自由度运动，以下按逆序分别进行阐述。

(1) 水动力学方程

在国际拖曳水池会议(ITTC)推荐定义[10]的基础上，给出本文所定义的舰船6自由度运动如图3所示，分别为线运动纵荡(surge)、升沉(heave)、横荡(sway)，以及转动运动横摇(roll)、艏摇(yaw)、纵摇(pitch)，其中Obxbybzb为船体坐标系。

理论上舰船的6个自由度运动之间是相互耦合的，但在实际计算中要建立一个完全精确的用于描述舰船运动的数学模型是相当困难的，也是不现实的。由于纵向运动(纵荡、升沉、纵摇)和横向运动(横荡、横摇、艏摇)之间的耦合作用较小，同时纵向运动中纵荡与其他2种运动的耦合作用也较小，因此可将舰船的6自由度运动拆分成3组，即纵荡运动方程、升沉-纵摇运动方程、横荡-横摇-艏摇运动方程[11]。在本节的研究中，选择忽略纵荡运动，认为舰船在xb轴向的运动速度等于航速，仅保留后2组方程如下：

升沉-纵摇运动方程：

(1)

横荡-横摇-艏摇运动方程：

(2)

式中：Aij，Bij，Cij为水动力系数；m，mij为质量、质量系数(t)；Iii为惯性矩(t·ft2，1ft=0.304 8 m)；yb，zb为升沉、横荡位移(ft)；γb，φb，θb为横摇、艏摇、纵摇角位移(rad)；Fi为扰动力和扰动力矩。

(2) 扰动力和扰动力矩

“提康德罗加”级巡洋舰基本上沿用了20世纪60年代末、70年代初研制的“斯普鲁恩斯”(DD - 963)级驱逐舰的舰体和动力装置，甚至外形设计也未作过大的修改[12]，因此在本节和下一节，直接应用麻省理工大学林肯实验室根据切片理论得到的“斯普鲁恩斯”级驱逐舰的水动力学特性作为“提康德罗加”级巡洋舰的一种近似替代。

舰船所受的扰动力和扰动力矩与航速、航向密切相关，在考虑不同自由度间的相位特性后，以遭遇浪高ηe为输入，到舰船所受扰动力和扰动力矩的拉氏变换表达式分别为[13]：

图2 切片理论研究步骤Fig.2 Research steps of strip theory

1)纵向扰动力和扰动力矩

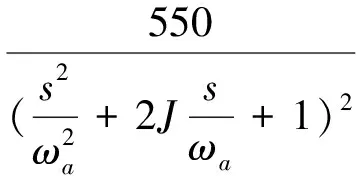
(3)

式中：J为常数，0.707；g为海面重力加速度(32.174 0 ft/s2)；ωm为海浪谱峰值角频率(rad/s)；U为航速(ft/s)；φ为风向角，即逆风向与航向间的夹角(°)；L为船长(ft)；B为船宽(ft)。

2)横向扰动力和扰动力矩

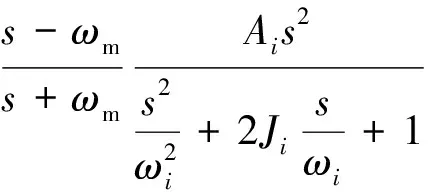
Ai=Ai0sinφ，

Ji=Ji0sinφ，

(4)

式中：A20=310，A40=2 120，A60=11 300，J20=0.72，J40=0.70，J60=0.35，ω20=0.60，ω40=0.76，ω60=0.96。

(3) 水动力系数

在忽略船尾部的附加质量系数和附加阻尼系数后，舰船水动力系数计算的简化公式详见文献[14]。同时，“斯普鲁恩斯”级驱逐舰的结构与水动力参数详见文献[15]。

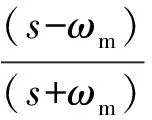
(4) 遭遇海浪谱

海浪谱是海面的功率密度谱，反映了海浪能量在波长和传播方向上的统计分布，它也是海面高度起伏相关函数的傅里叶变换。海浪谱是描述海面最基本的方法之一，现有的各种海浪谱大多为半经验、半理论的结果，包括Neumann谱、PM谱等，每种海浪谱的公式推导方法和测量海域环境均有较大差异，尚为形成统一认识[16]。

然而，上述海浪谱是在静止条件下观测到的，属于绝对海浪谱。在航行条件下，舰船与海浪间的相对运动将产生遭遇海浪谱，且遭遇海浪谱与绝对海浪谱间满足能量守恒原则。以Bretschneider谱为基础得到的遭遇海浪谱为[17]

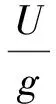
γ(α)=0.917 4α+0.990 3，ω0=γ(α)ωm，

(5)

有了遭遇海浪谱，便可以生成满足谱特性的随机海浪。通常的做法是将遭遇海浪谱设计成滤波器，并以高斯白噪声w为输入在频域进行模拟。与Bretschneider遭遇海浪谱对应的传递函数为[17]

(6)

2.2数学仿真

由式(1)～(4)，(6)可知，从原始输入的高斯白噪声w到最终输出的舰船5自由度运动yb，zb，γb，φb，θb，中间涉及了遭遇浪高ηe以及扰动力和扰动力矩Fi等多个变量，且相应的常微分方程与传递函数的阶数均较高，若分开进行计算将较为耗时，实际计算时可将所有模型整合为状态空间模型进行数学仿真。

针对纵向运动和横向运动分别选取了2组状态，并与文献[13]中同状态下的仿真结果进行了对比，5个自由度运动的幅度与周期特性均较为吻合，从而证明了本文水动力学模型的可信性。以下仅给出升沉运动的仿真结果对比如图4所示。

图4 升沉运动Fig.4 Heaving motion

3 动态散射特性

为生成动态散射回波，首先需将一维距离像所蕴含的散射点位置信息以及舰船3自由度转动运动所蕴含的角速度信息向船体坐标系进行变换，进而计算散射点的幅度、时延、多普勒信息并最终生成整个舰船的动态散射回波。

3.1船体坐标系下的参数变换

(1) 散射点位置变换

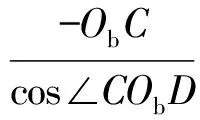
图5 散射点位置Fig.5 Location of scattering point

(2) 转动角速度变换

(7)

3.2动态散射回波生成

一维距离像中任一散射点Ci的运动速度vCi借由xb轴上对应点Di进行计算的公式如下。可见，由于简单地认为一维距离像中的散射截面仅由船体xb轴上的结构贡献，忽略了船体结构的宽度和高度信息，式(8)中的速度计算也相应较为粗糙。

(8)

设视线AOb方向的单位向量为dT，雷达波长为λ，则散射点Ci的多普勒频率fdi为fdi=-2(vCi·dT)/λ。

设雷达发射峰值功率为Pt，一维距离像中任一散射点Ci的雷达散射截面为σi，径向距离为Ri，视线AOb方向的天线增益为G，衰减因子为L，则由散射点Ci贡献的回波功率为

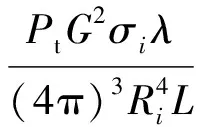
(9)

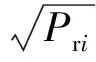
最后，以线性调频波为例给出某一视线方向下舰船动态散射回波的计算公式。设一维距离像中散射点的个数为N，调频斜率为K，任一散射点Ci的时延为τi=2Ri/c，则动态散射回波为

(10)

综上，生成动态散射回波的全流程如图6所示。

4 仿真分析

本节主要考察“提康德罗加”级巡洋舰在不同海况条件下雷达回波的稳定特性。为均衡激发舰船的纵向运动与横向运动，取风向角φ=45°；取航速U=21 ft/s，约为最大航速的一半；另外，将道氏海况等级[18]与蒲氏风情等级[19]按照风速的范围作简单对应如表1所示，仿真时将有义波高范围的中值作为各级海况条件下h1/3的取值。

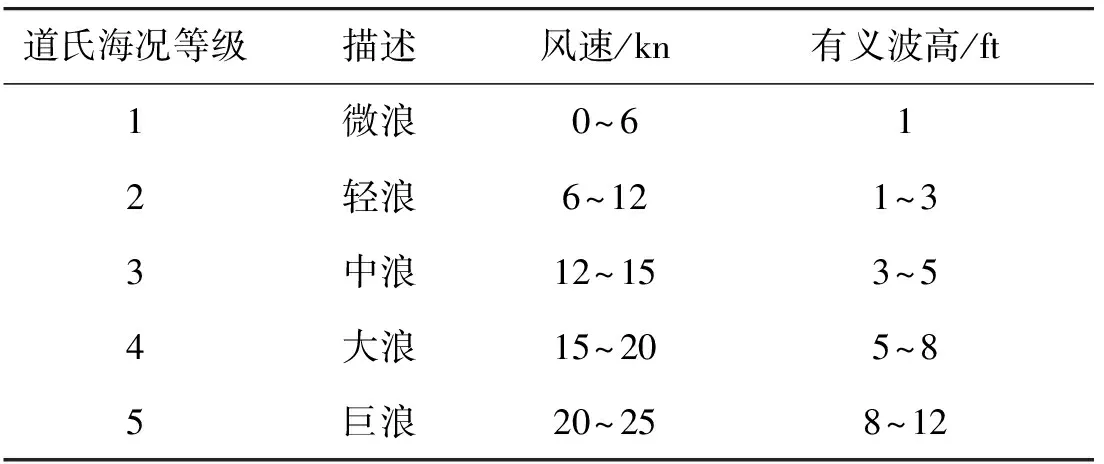
表1 海面状态Table 1 Sea state

注：1kn=1.852 km/h;1ft=0.304 8m。

与雷达有关的参数此处省略。仿真方案设定为雷达平台静止，且与舰船中心的初始距离为30 km。仿真中未考虑不同入射角度下海杂波的影响，仅以固定信噪(杂)比15 dB进行分析。

入射余角选取0°～80°，方位角选取0°～90°，角度间隔均为10°。每个入射余角×方位角的角度组合做10次稳定性分析，每次分析50帧数据，并记录最稳定散射点的稳定性测度。稳定性测度即指距离-多普勒二维图中散射点连续稳定在某一二维分辨单元中的帧数。将同一入射余角下所有0°～90°方位角×10次的稳定性测度取均值得到该入射余角下的稳定性估计如图7所示，可见随着海况的升高，舰船回波的稳定性相应下降。另外，高入射余角由于引入了更多的径向多普勒变化，相比同一海况下的低入射余角回波稳定性稍低。

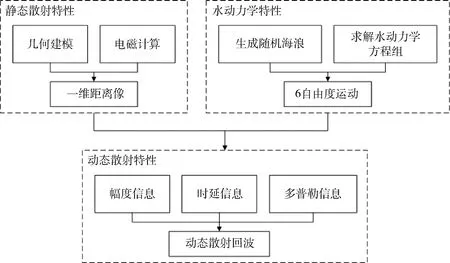
图6 动态散射回波全流程Fig.6 Whole procedure of generating dynamic scattering echo

图7 回波稳定性估计Fig.7 Stability estimation of echo

另外如图8所示，对一级海况下入射余角5°时录取的某导弹护卫舰回波数据进行统计分析，最稳定散射点的稳定性测度为39，相比图7中同条件下“提康德罗加”级巡洋舰的稳定性稍低，可认为是由于该舰的吨位较低，相应的质量与转动惯量较小，导致6自由度运动的周期较小同时幅度较大，从而散射点在距离-多普勒二维图中某一二维分辨单元的稳定帧数较少。在合理外推的范围内，该导弹护卫舰的外场实测数据可为本文模型的正确性提供一定程度的支撑。

图8 某导弹护卫舰回波稳定性Fig.8 Echo stability of the missile destroyer

5 结束语

本文为了在仿真条件下获取舰船的动态散射回波数据，在静态散射特性和水动力学特性环节均进行了较为精细的建模，虽然初步得到了舰船的稳定性估计，但仍有诸多不足之处。后续有待深入研究的内容包括3部分：①由于静态散射特性数据为一维距离像格式，散射点的位置只能简单认为在xb轴上，后续可考虑直接采用与舰船三维空间结构对应的散射中心格式；②舰船的水动力学特性没有考虑姿态稳定控制的影响，后续可考虑加入姿态控制模型或直接录取舰船6自由度运动的外场数据；③验模部分所采用的导弹护卫舰在吨位上与“提康德罗加”级巡洋舰存在较大差距，佐证力度不足，需获取吨位相近舰船的外场实测数据进行统计分析。

经统计分析所获得的舰船回波稳定性估计可为工程应用提供一定的参考与借鉴。舰船回波的稳定性是一项重要的统计特性，可作为区分部分无源、有源干扰的识别判据，相信随着目标特性领域研究的不断深入，还会有更多的区分特性被挖掘出来。

[1] 陈秋菊.面向识别的舰船目标雷达回波仿真与特性分析[D]. 长沙: 国防科学技术大学, 2007:8-15.

CHEN Qiu-ju.Recognition-Oriented Simulation and Characteristics Analysis of Radar Echoes for Ship Targets[D]. Changsha: National University of Defense Technology, 2007:8-15.

[2] 张安, 卢再奇, 范红旗, 等. 基于散射中心模型的舰船LFM雷达回波仿真[J]. 雷达科学与技术, 2011, 9(4):316-320.

ZHANG An,LU Zai-qi,FAN Hong-qi, et al. Echo Simulation of LFM Radar for Ship Target Based on Scattering Center Mode[J]. Radar Science and Technology, 2011, 9(4):316-320.

[3] 许小剑, 姜丹, 李晓飞. 时变海面舰船目标动态雷达特征信号模型[J]. 系统工程与电子技术, 2011, 33(1):42-47.

XU Xiao-jian, JIANG Dan, LI Xiao-fei.Modeling of Dynamic Radar Signatures for Ships on Time-Varying Sea Surface[J]. Systems Engineering and Electronics, 2011, 33(1):42-47.

[4] 韩晓光, 吴晞. 穿浪双体船纵摇和垂荡运动研究[C]∥2009航海技术理论研究论文集, 2009:7.

HAN Xiao-guang, WU Xi. Research on Pitching and Heaving Motion of WPC[C]∥2009 Seamanship Theory Researching Memoir, 2009:7.

[5] 庞洪林. 基于CFD的高速三体船侧体构型优化研究[D]. 大连: 大连理工大学, 2015.

PANG Hong-lin. Optimization on the Side-Hull Configuration of Trimaran Based on CFD Method[D]. Dalian: Dalian University of Technology, 2015.

[6] 张金亮. 迎浪状态下高速双体船的运动响应计算[D]. 天津: 天津大学, 2009.

ZHANG Jin-liang.Calculating the Dynamic Response ofHigh-Speed Catamarans in Head Waves[D]. Tianjin: Tianjin University, 2009.

[7] 韩晓光, 杨艳明, 郭航. 基于切片法的高速船摇荡运动预报研究[J]. 广州航海高等专科学校学报, 2009, 17(4):7.

HAN Xiao-guang, YANG Yan-ming, GUO Hang. Research on Prediction of the Swing Motion of High Speed Vessel Based on Strip Theory[J]. Journal of Guangzhou Maritime College，2009, 17(4):7.

[8] 闵波. 箱形船在波浪上的运动计算[D]. 武汉: 武汉理工大学, 2007.

MIN Bo. The Method for the Estimation of Motions of Box-Shaped Ship in Waves[D]. Wuhan: Wuhan University of Technology, 2007.

[9] 王学亮. 大型起重船在海浪中的运动响应研究[D]. 天津:天津大学, 2004.

WANG Xue-liang. Study on Wave-Induced Motion of the Large Derrick Barge Ships[D]. Tianjin: Tianjin University, 2004.

[10] ITTC Symbols and Terminology List Final Version 1996[C]∥International Towing Tank Conference, 1997.

[11] 魏纳新. 水面舰艇在高海情下的横摇运动姿态控制技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2006.

WEI Na-xin.Roll Control Technique Research of Surface Ship in Extreme Sea Condition[D]. Harbin: Harbin Engineering University, 2006.

[12] 海军装备论证研究中心. 美国海军武器装备手册[M]. 北京: 解放军出版社, 2000.

Naval Equipment Demonstration and Research Center. US Naval Weapon & Equipment Handbook[M]. Beijing: Chinese Peoples Liberation Army Publishing House, 2000.

[13] TRIANTAFYLLOU M, BODSON M, ATHANS M. Real Time Estimation of Ship Motions Using Kalman Filtering Techniques[J]. IEEE Journal of Oceanic Engineering, 1983, 8(1):9-20.

[14] Nils Salvesen, TUCK E O, Odd Faltinsen. Ship Motions and Sea Loads[J]. Transactions-Society of Naval Architects and Marine Engineers, 1971, 78:1-30.

[15] Design Lab., Ocean Eng., Dept., MIT, Cambridge, MA. 5-Degree of Freedom Seakeeping Program Manual[R]. 1979.

[16] 许小剑, 李晓飞, 刁桂杰, 等. 时变海面雷达目标散射现象学模型[M]. 北京: 国防工业出版社, 2013.

XU Xiao-jian, LI Xiao-fei, DIAO Gui-jie, et al. Radar Phenomenological Models for Ships on Time-Evolving Sea Surface[M]. Beijing: National Defense Industry Press, 2013.

[17] TRIANTAFYLLOU M, BODSON M. Real Time Estimation of Ship Motions Using Kalman Filtering Techniques[R]. Report of Lab. Info. Decision Syst. MIT, USA, 1981:1090-1095.

[18] 许小剑, 黄培康. 雷达系统及其信息处理[M]. 北京: 电子工业出版社, 2010.

XU Xiao-jian, HUANG Pei-kang. Radar System and the Information Processing[M]. Beijing: Electronic Industry Press, 2010.

[19] MERRILL I， Skolnik. 雷达手册[M].3版.南京电子技术研究所译，北京: 电子工业出版社, 2010.

Merrill I， Skolnik. Radar Handbook[M].3rd ed.Nanjing Electronic Technology Institute Translated. Beijing: Electronic Industry Press, 2010.

ModelingofDynamicScatteringEchoofShipandStabilityAnalysis

YU Xin-yuan1,2，XU Bo3，XIONG Kun4，DU Hai4

(1.Beijing Mechanical & Electrical Overall Design Department, Beijing 100854, China; 2.The Second Academy of CASIC, Beijing 100854, China;3.The Delivery Technology Academy of CASIC, Beijing 102308, China;4. Beijing Institute of Remote Sensing Equipment, Beijing 100854, China)

The scattering characteristics of ship under dynamic conditions are of great value for target recognition. Taking Ticonderoga-class cruiser for an example, the method of obtaining static scattering characteristics data of ship is briefly introduced at first. Then, the whole hydrodynamic model is built based on strip theory, and next the simulation of the dynamic scattering echo of ship is carried out. Finally, the estimation of echo stability under different sea states and grazing angles is achieved through statistically analyzing the simulation data, and its credibility is indirectly demonstrated by comparing with the field collected data. The research results could offer some theoretical support for sea surface radar target recognition.

ship; static; strip theory; dynamic; scatting; echo stability

2016-09-28；

2016-12-13

于新源(1988-)，男，黑龙江牡丹江人。博士生，主要研究方向为电子对抗。

通信地址：100854 北京市142信箱206分箱6室E-mail：yuxinyuan.23@163.com

10.3969/j.issn.1009-086x.2017.05.027

TN955+.2;N945.12

A

1009-086X(2017)-05-0170-08