轴承腔内壁与油膜换热的数值模拟与试验
2017-11-20胡剑平任国哲易军刘振侠吕亚国赵静宇
胡剑平, 任国哲, 易军, 刘振侠, 吕亚国, 赵静宇
1.西北工业大学 动力与能源学院, 西安 710072 2.陆军航空装备发展办公室, 北京 100021
轴承腔内壁与油膜换热的数值模拟与试验
胡剑平1,*, 任国哲1, 易军2, 刘振侠1, 吕亚国1, 赵静宇1
1.西北工业大学 动力与能源学院, 西安 710072 2.陆军航空装备发展办公室, 北京 100021
航空发动机后轴承腔内壁与滑油的换热分析是轴承腔热防护结构设计的基础。对航空发动机轴承腔内壁换热模拟试验件开展试验与数值模拟研究,得到了滑油油膜对轴承腔内壁的换热影响。通过测量试验件外壁面、内壁面以及滑油油膜的温度得到了试验件内壁面换热热流密度与换热系数的分布;结合CLSVOF(Coupled Level Set and Volume Of Fluid)油/气两相流以及热-流-固耦合计算方法对试验件进行了换热分析,并将内壁对滑油的局部热流量的计算结果与试验结果进行了对比,结果显示两者在各个工况下均吻合较好。通过将局部换热系数计算值与当地的滑油流动雷诺数Rel进行对比分析,结果显示内壁局部努赛尔数Nuw与Rel的0.7次方成正比关系。另外,对转速对换热的影响进行分析得到Nuw与旋转雷诺数Rerot的0.345 次方呈正比关系。
航空发动机; 后轴承腔; 换热; 滑油油膜; 试验研究; 数值模拟
轴承腔内的油气两相流流动与换热研究对于优化轴承腔热防护结构的设计,从而改善和防止轴承腔内滑油的结焦和着火问题具有重要意义,是目前国内外先进航空发动机润滑系统研制的热点与焦点[1-3]。
目前国内外已经对轴承腔内油气两相流的流动开展了大量而系统的研究工作,如Karlsruhe大学的Glahn和Wittig[4]对Trent发动机某轴承腔内油滴运动及空气流动进行了光学测量;Bai[5]和Farrall[6]等通过理论与试验研究建立了液滴与壁面的撞击特性;Simmons[7]和Wolfram等[8]分别采用欧拉-拉格朗日与VOF (Volume Of Fluid)方法对轴承腔内的油气两相流进行了数值模拟。不过当前的研究成果主要集中在轴承腔内油气两相流流动与壁面油膜流动问题上,而对于轴承腔壁面的换热研究相对较少。Glahn等[9-10]测量了Trent 发动机某轴承腔腔壁的温度分布以及内壁附近油气温度,并采用了二维分析方法,得到轴承腔油气两相流环境下的平均换热系数与滑油流量、转速、腔室几何参数等变量的经验关系式;在此基础上,Busam等[11]进一步考虑腔室几何结构的影响,并将各因素总结成相应无量纲参数,形成平均换热系数的无量纲参数努赛尔数Nu的表达式。然而,Busam得到的经验公式是平均换热系数与腔室工作参数的关系式,其应用范围有很大局限,仅限于其试验研究的轴承腔。国内对于轴承腔腔内油气两相流开展了大量数值计算研究与试验研究。陈国定等[12]在滑油油滴变形与运动以及油膜流动一维运动分析上开展了研究工作;刘振侠等[13-14]对腔内油气两相流以及壁面油膜厚度的测量方法进行了系统研究。
在目前轴承腔热分析的工程研究中,滑油腔体内壁对流换热近似采用流体外掠平板的对流换热计算公式,即滑油物性参数以滑油出口温度为定性温度,特征长度一般取轴承腔内壁直径或者特征截面直径,特征速度一般取轴承保持架线速度的1/3[15]。然而根据Glahn[16]和刘振侠[17]等的一维理论求解结果以及其他关于内壁油膜运动的研究结果显示在轴承腔内的两相流场中,轴承腔内壁面滑油较多,此时的两相流流动速度要比轴承转速线速度的1/3要小得多,因此,特征速度选取轴承保持架线速度的1/3会给轴承腔壁的换热计算带来很大误差。轴承腔的热分析主要包括两方面内容:一方面是从特定轴承腔结构得到轴承腔均匀换热系数,以修正航空发动机润滑系统整体热分析,如文献[15];另一方面是分析轴承腔表面油膜运动得到轴承腔壁面的局部换热系数,其研究结果具有一定的通用性。
为分析发动机后轴承腔发动机结构对轴承腔内传热特性的影响,本文对轴承腔油气两相流模拟件表面的换热进行了试验研究,结合腔内两相流流场计算与轴承腔表面油膜厚度试验测量,得到轴承腔表面的换热系数关系式。
1 轴承腔内壁换热模拟试验
1.1 轴承腔换热模拟试验件
本文中的试验是在西北工业大学轴承腔内油气两相流模拟试验台开展的,该轴承腔换热模拟试验件采用航空发动机轴承腔材料1Cr18Ni9Ti,根据某发动机轴承腔的工作状态,完成了该试验件的设计与加工,其剖视图如图1所示。因为该试验件是为了分析发动机高温部件结构对后轴承腔内传热的影响,因此采用试验腔体外加热方式进行试验。
滑油由轴承15的右端喷入轴承腔,通过甩油结构11与旋转盘12的旋转,滑油被雾化成细小的颗粒,并甩向轴承腔中,形成空气-滑油两相流流场,一部分滑油在轴承腔壁8的内壁面形成油膜,另一部分从回油孔流出;加热腔外壳与轴承腔壁面共同形成了加热腔,加热到一定温度的空气通过管路进入到加热腔内对轴承腔壁8进行加热,最后从排气管路排出。
试验过程中轴承腔内壁表面上油膜厚度采用自制的超声测量系统进行测量[14],试验过程中通入加热腔的热气温度范围为50~75 ℃,滑油采用美孚飞马2号航空润滑油(Mobile Jet Ⅱ),滑油流量范围为200~400 L/h,旋转转轴转速为1 500~4 500 r/min。

图1 试验件剖视图Fig.1 Section view for test rig
在轴承腔外壁面、内壁面及轴承腔内均布置了K型热电偶丝进行温度测量,温度测点沿轴向的分布示意图如图2所示,内壁温度测点位于试验件周向方位角θ=225° 处。热电偶丝布置位置沿轴向从左至右距左边腔壁的距离依次为L1=0.065 m,L2=0.090 m,L3=0.110 m,L4=0.125 m,L5=0.140 m,L6=0.155 m。其中滑油油膜的热电偶布置距离内壁面2 mm,在油膜厚度的计算与测量中显示该6个测点处于滑油油膜内。由于同一轴向位置处需要布置3个热电偶,在实际安装热电偶丝过程中,为尽量降低安装孔对结构换热的影响,安装孔径为0.2 mm。同时外壁面热电偶丝焊点偏离1.5°,油膜温度测点偏离-1.5°。在试验设计中忽略温度在θ=223.5°~226.5° 范围内沿周向分布的差异,这参考了Karlsruhe大学对Trent发动机后轴承腔的温度测量方法[9],因此该换热测量试验实际是将轴承腔三维的换热问题简化成二维换热的测量。为了降低加热对周向不均匀的影响,加热气的进口布置在θ=90° 处。由于该试验件没有沿周向布置热电偶,因此对于试验过程中周向分布差异没有进行验证,这需要在今后的试验改造中进行改善。
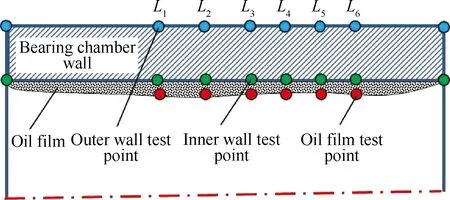
图2 试验件温度测点沿轴向分布 Fig.2 Axial distribution of temperature test points oftest rig
1.2 轴承腔壁局部换热系数
轴承腔壳体的外壁面温度较高,内壁面温度较低,外壁面向内壁面为热传导过程,内壁面与滑油为对流换热过程,本文通过试验测量得到轴承腔壁面、油膜等温度后,具体轴承腔壁面局部换热系数的求解如下:
由傅里叶导热定律可知导热量为

(1)
式中:dQ1为微元沿y方向上的热流量;∂Tw/∂y为腔体壳体温度Tw沿y方向的变化率;λw为壁面材料导热系数;dA1为腔壁换热表面单元面积。
轴承腔内的滑油与轴承腔内壁面之间为对流换热过程,由牛顿对流换热公式可知,油膜与内壁面的换热量为
dQ2=hdA2ΔT
(2)
式中:dQ2为对流换热量;h为滑油与轴承腔内壁面之间的局部对流换热系数;ΔT为滑油与轴承腔内壁面之间的温差;dA2为油膜与壁面接触表面单元面积。
由dQ1=dQ2与dA1=dA2可得
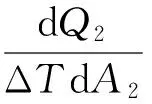
(3)
ΔT的表达式为
ΔT=Tl-Tw_i
(4)
式中:Tl为滑油温度;Tw_i为轴承腔内壁面温度。
对于∂Tw/∂y的计算方法,在轴承腔腔体上沿周向取面积为dA的微元,则此时微元对应的腔体外壳导热可近似为平板稳态导热,则有

(5)
式中:Tw_o为轴承腔外壁面温度;dw为轴承腔壳体厚度。联立可得滑油与内壁面的对流换热系数为

(6)
2 轴承腔壁面的热-流-固数值计算
为了模拟真实发动机后轴承腔的腔体结构对腔内油气换热的影响,结合本文的试验件结构,构建的计算几何模型如图3所示,计算区域包括固体腔体域与腔内油气两相流体域2个部分。在试验过程中采用腔体外热空气对腔体进行加热,通过热电偶丝测定试验腔体外壁面温度分布。在计算过程中,腔体固体区域的外边界在径向方向选在外表面,并将试验测量温度值作为第一类边界条件;在轴向方向两侧,由于试验过程中采用了隔热措施,因此两侧采用绝热边界。

图3 试验件计算模型Fig.3 Computational model for test rig
图中下方的绿色直管为回油管,图3(b)中,红色区域为旋转轴,滑油从转轴的台阶处喷出并被甩到轴承腔内,黄色区域为轴承腔壁。旋转轴较小半径rshaft_1为71.5 mm,此部分对应的长度Lshaft_1为115 mm;旋转轴较大半径rshaft_2为82.5 mm,此部分对应的长度Lshaft_2为95 mm;轴承腔内壁面半径rshell_i为119.5 mm,轴承腔外壁面半径rshell_o为144.5 mm;回油管长度Loil为40 mm,回油管直径doil为20 mm,回油管轴线位于转轴台阶处。
对于轴承腔内油气两相流流动,本文采用耦合Level Set的VOF方法,即CLSVOF(Coupled Level Set and VOF)方法对轴承腔内油气两相流动进行计算[18]。Chandra等[19]在分析轴承腔回油结构特性时将此方法进行了成功应用;刘振侠等[20-21]在研究工作中已经采用该方法对轴承腔内部流场进行了数值仿真,并将计算结果中轴承腔壁面油膜厚度的计算结果与欧拉-拉格朗日计算及试验结果进行了对比,验证了CLSVOF方法在计算轴承腔内部油气两相流时具有较高的准确性,且与欧拉-拉格朗日方法相比,CLSVOF方法具有计算量相对较小、能准确捕捉轴承腔表面油膜脱离现象的优点。
在下文数值计算以及试验结果分析中将重点分析轴承腔内壁与滑油的换热,从换热热流密度的试验测量值与计算值的对比分析中也能证明计算方法的准确性。
在CLSVOF方法求解过程中,需要分别对体积函数F(x,t)(x为计算网格单元,t为时间)和距离函数Φ(x,t)进行求解。F(x,t)来自于VOF方法思想,表示流体在每个计算网格单元中所占的体积分数。在本文中体积函数F(x,t)定义为

因此,采用CLSVOF方法得到的两相流动控制方程(包括质量守恒方程、动量方程、能量守恒方程)为
(7)
(8)
(9)
式中:p为压力;g为重力加速度;E为内能;keff为有效热导率;Sh为能量方程的源项;U为流体流动速度;ρ和μ分别为密度和动力黏度;T为控制单元平均温度;Fσ为表面张力。文中采用连续表面张力(CSF)模型[19]来求解,文献[19]中采用这一模型很好地捕捉了轴承腔内滑油与空气的分界。
Fσ的表达式为
(10)
式中:σ为表面张力系数;κ为表面曲率;δ(Φ)的表达式为
(11)
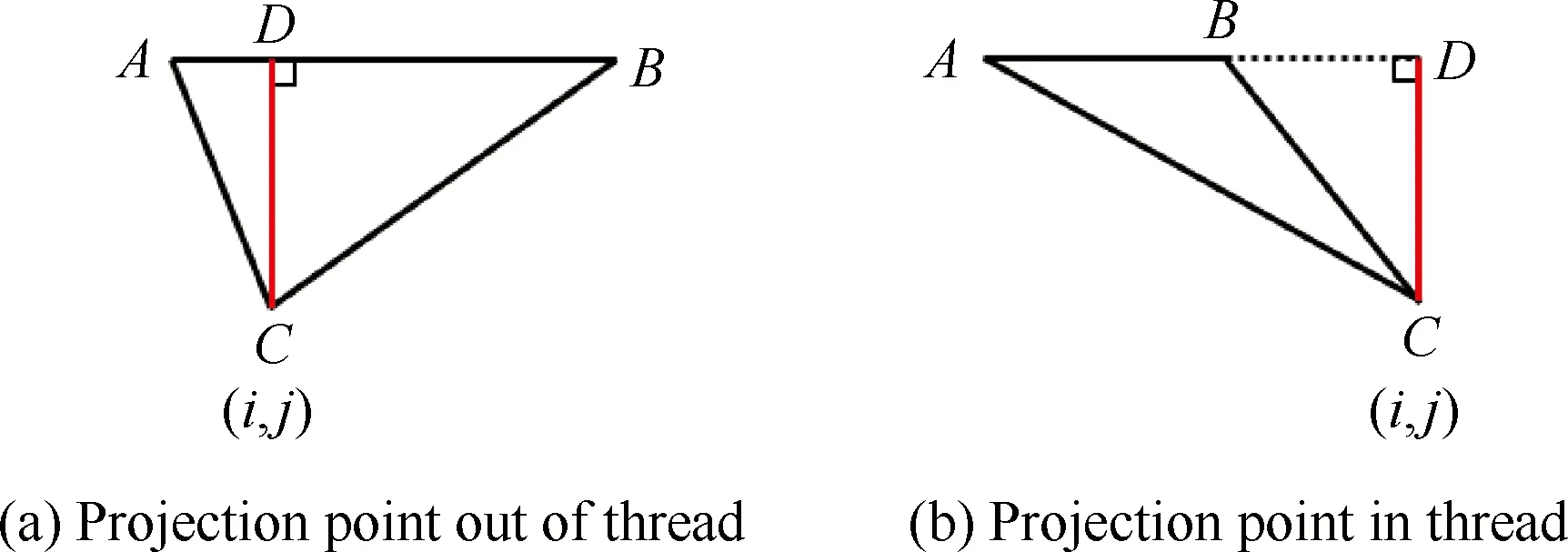
图4 距离函数Φ的重新初始化示意图 Fig.4 Schematic view of re-initialization for distance function Φ
其中:H(Φ)为关于Φ的函数;a为最小网格尺度的1.5倍。在CLSVOF方法中,采用几何法对距离函数Φ(x,t)重新初始化。图4为采用几何法对Φ(x,t)重新初始化的示意图,图中线段AB表示两相界面,点C表示网格(i,j)的中心,Φ(x,t)初始化的实质就是获取网格中心点到界面的最小距离,因此当C在AB上的投影点D位于线段AB上时,如图4(a)所示,线段CD的长度就是最小距离;当投影点D在线段AB的延长线上时,如图4(b)所示,最小距离取线段AC和BC中长度较小的线段。
按照此方法确定网格(i,j)到界面的所有距离后,通过比较可得到网格(i,j)到界面的最小距离Hmin,采用体积函数F(Φ,t)对相应的Φ重新初始化,其表达式为
Φ=Hminsign(0.5-F(Φ,t))
(12)
由于前期的工作已经通过该试验件的油膜厚度试验数据对计算方法的准确性进行了验证,同时也分析了腔内油气两相流滑油-空气的分布、滑油油膜运动等细节[20-21]。因此,下文将对轴承腔内壁的换热试验及计算进行分析与讨论。
3 轴承腔内壁面局部换热
3.1 腔壁温度变化试验测量
在试验过程中,先向加热腔内通入热气,待腔壁温度稳定后(t=0时刻)向转轴通道通入滑油。图5~图7为加热空气温度为75 ℃、滑油初始温度为25 ℃、滑油流量为200 L/h试验条件下通入滑油后轴承腔壁外壁面温度、内壁面温度以及内壁表面换热热流密度的动态测量结果。从图5可见外壁面各测点的温度逐渐降低,这是由于通入滑油后,热量从外壁传递到滑油对滑油进行加热,当时间t=210 s左右时,各测点的温度以及热流量逐渐达到稳定。在下文的换热试验结果分析中均采用t∈[300,600] s时间段内的测点温度及换热热流密度进行计算。相比于各个测点温度的变化,试验过程中滑油油膜的厚度在2~3 min后才能达到基本稳定[14]。

图5 试验开始阶段轴承腔外壁面温度变化Fig.5 Change of bearing chamber outer wall temperature at test start stage
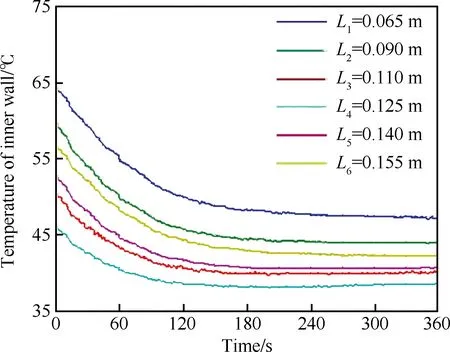
图6 试验开始阶段轴承腔内壁面温度变化Fig.6 Change of bearing chamber inner wall temperature at test start stage

图7 试验开始阶段局部换热热流密度变化Fig.7 Change of local heat flux density at test start stage
3.2 局部换热热流密度试验结果与数值计算对比
采用CLSVOF方法建立了换热计算模型,针对试验各个工况进行数值计算,获得了试验测量位置处的热流量,将计算结果与试验数据进行了对比分析。
图8为壁面加热温度为50 ℃、滑油质量流量为200 L/h情况下,转速分别为1 500、3 000和4 500 r/min 时,轴承腔壁面与腔内两相流的换热热流密度计算值(CFD)与试验值(Test)的对比。图中:Ta为通入到加热腔的加热空气温度;qoil为通入到试验件的滑油流量;ns为旋转件的转速。3个转速下局部换热热流密度最大值均出现在轴向位置0.12 m附近,这个位置处于试验件轴承腔滑油喷射出口轴向位置,被旋转轴甩出的滑油大部分直接接触到了此处的壁面,在该处滑油油滴与壁面发生撞击可能导致液滴的黏附、飞溅等现象,并且该处的滑油在轴向的速度也较大[17],这些物理过程都会加强局部的换热,因此会在局部形成一个峰值。
对比3个不同转速下的局部换热图可以看出,换热热流密度随转速的增大而增大,这是因为一方面转速增大导致了轴承腔壁面附近流场湍流度增大,有利于换热的进行;另一方面是由于随着转速的增大,滑油受到的切向动量以及空气的剪切力均会增大,回油速率增加,滑油循环效率增加。另外,随着转速的增加,轴承腔靠近轴向两侧的换热热流密度有明显增加,并且转速越高,增加越明显。这可能是由于试验件设计中轴向长度较大,在两侧滑油油膜厚度相对较薄,两侧油膜运动速度对空气的剪切作用更敏感,转速变化将会直接导致油膜速度增加,最终导致换热加强。

图8 热流密度计算与试验结果对比(Ta=50 ℃,qoil=200 L/h)Fig.8 Comparison between CFD and test results for heat flux density (Ta=50 ℃,qoil=200 L/h)
图9为壁面加热温度为50 ℃、滑油质量流量为400 L/h情况下,转速分别为1 500和3 000 r/min 时,轴承腔壁面与腔内两相流的换热热流密度计算值与试验值的对比。图9与图8的对比显示在滑油流量增加一倍的情况下,腔内壁与滑油的换热热流密度明显上升,但是并不呈正比增加。
图10为加热空气温度为75 ℃、滑油质量流量为200 L/h情况下,转速分别为1 500、3 000和4 500 r/min时,轴承腔壁面与腔内两相流的换热热流密度计算值与试验值的对比。这3个工作条件下轴承腔内壁与油膜的局部换热随转速的变化与加热空气温度为50 ℃时相同,在轴向0.12 m附近出现极大值;换热热流密度均随转速增加而增大;高转速条件下,轴承腔轴向两侧换热热流密度都有明显上升。
但是,对比图10与图8可以看出当滑油流量与转速均相同时,外加热空气温度越高,腔壁与滑油的换热越强。其原因可能有两方面:一方面是温差变大,换热加强;另一方面可能由于滑油黏性的下降导致对流换热加强。由于外加热空气越高,通过传热也会导致滑油温度上升,由此滑油黏性下降。在20~75 ℃范围内,滑油黏性随温度变化非常剧烈,滑油黏性下降将会导致滑油油膜运动速度增加,最终强化了壁面与油膜的换热。
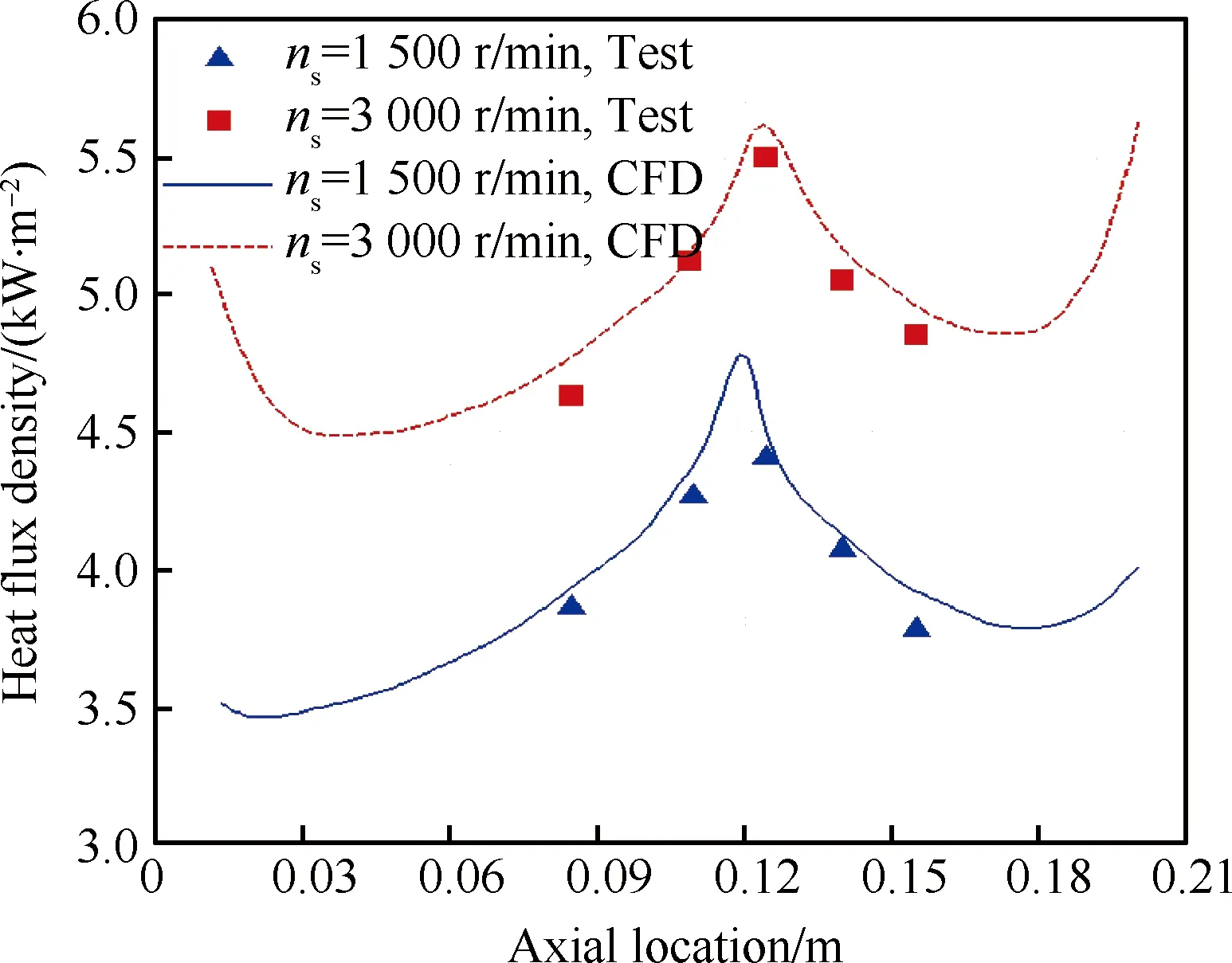
图9 热流密度计算与试验结果对比(Ta=50 ℃, qoil=400 L/h)Fig.9 Comparison between CFD and test results for heat flux density (Ta=50 ℃, qoil=400 L/h)
图11为壁面加热温度为75 ℃、滑油质量流量为400 L/h情况下,转速分别为1 500和3 000 r/min 时,轴承腔壁面与腔内两相流的换热热流密度计算值与试验值的对比。图11中腔壁与油膜的换热沿轴向的分布以及与图9结果的对比均符合前文分析规律。
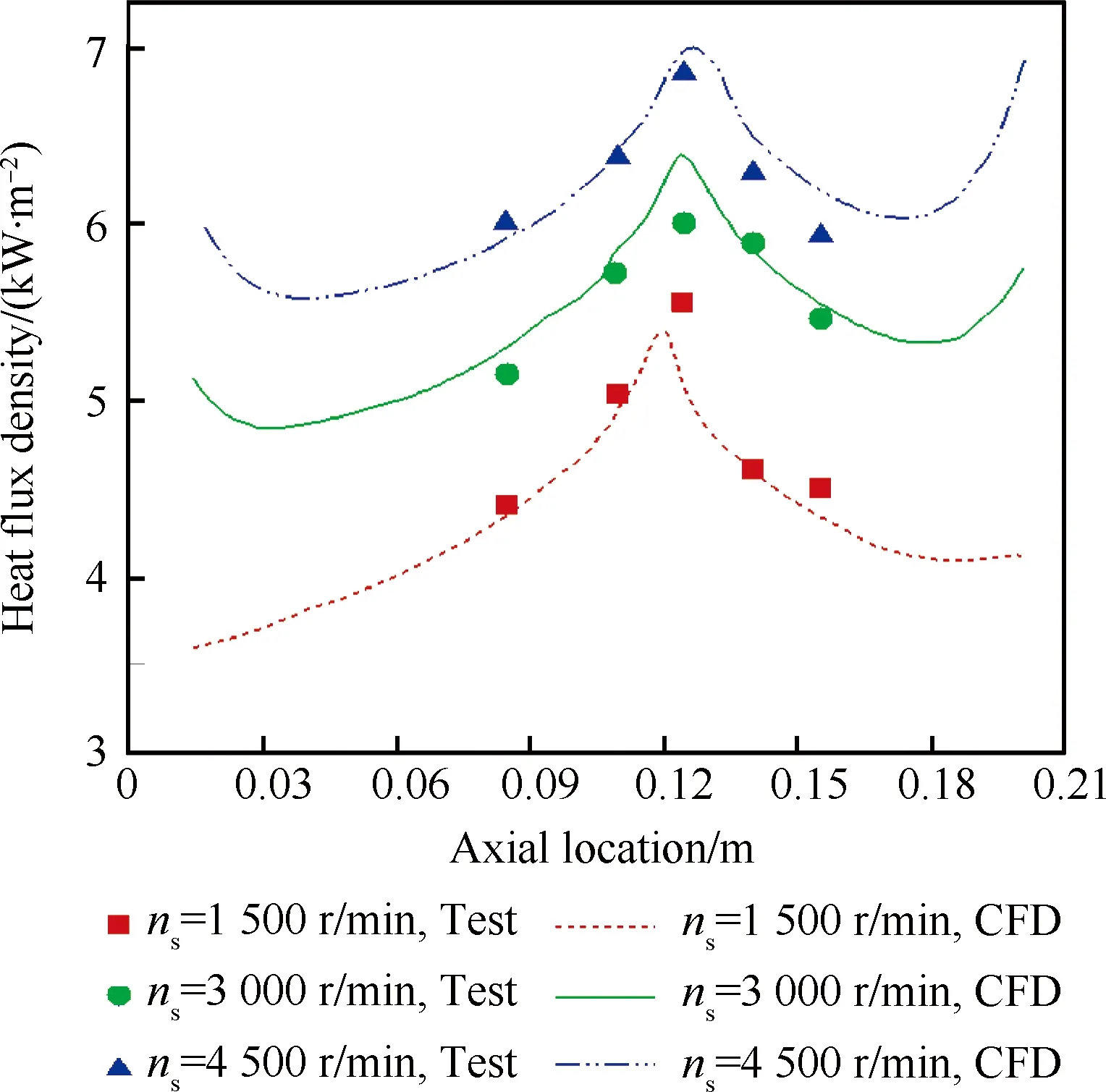
图10 热流密度计算与试验结果对比(Ta=75 ℃, qoil=200 L/h)Fig.10 Comparison between CFD and test results for heat flux density (Ta=75 ℃, qoil=200 L/h)
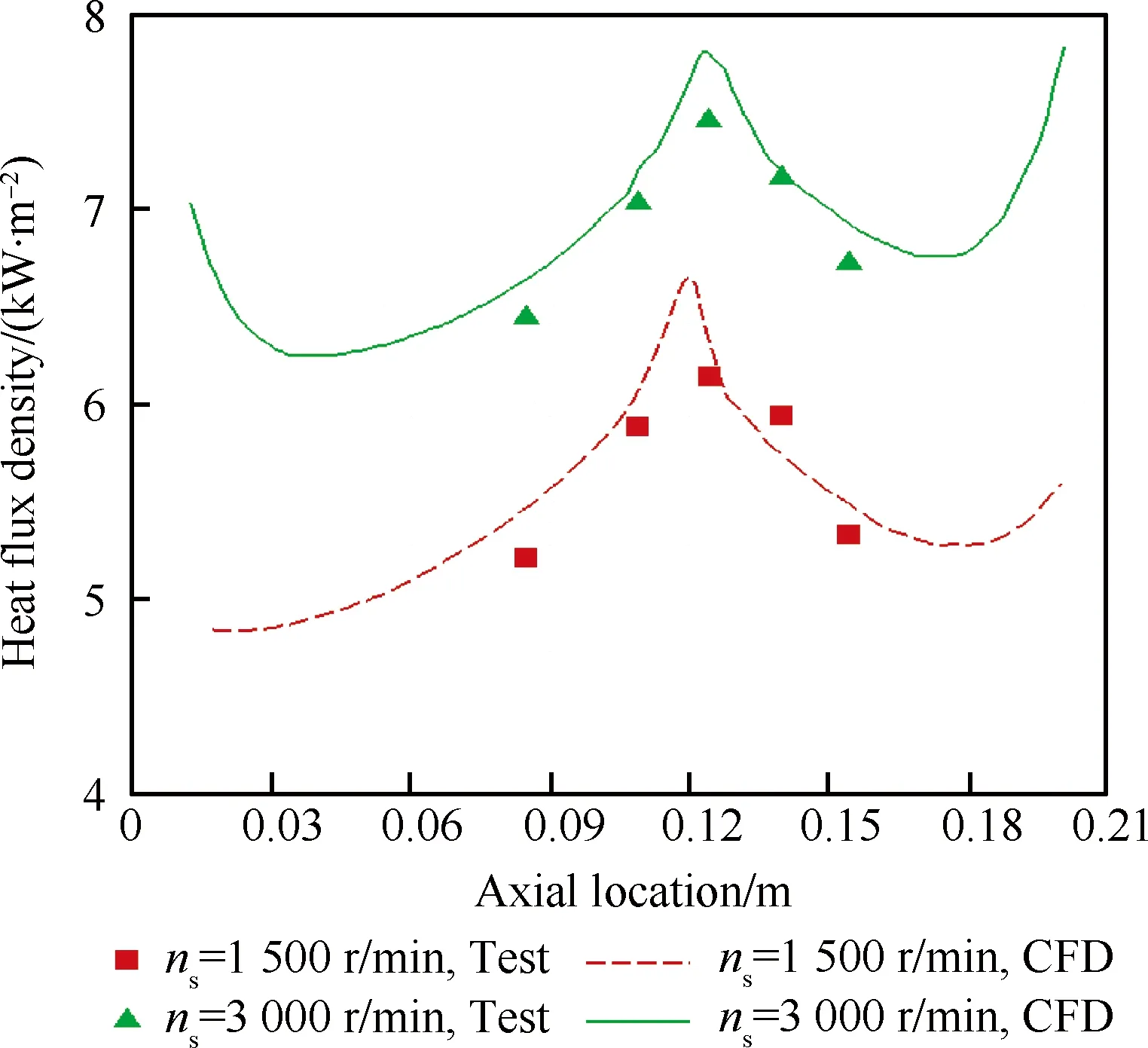
图11 热流密度计算与试验结果对比(Ta=75 ℃, qoil=400 L/h)Fig.11 Comparison between CFD and test results for heat flux density (Ta=75 ℃, qoil=400 L/h)
由图8~图11可以看出,壁面换热热流密度的计算值与试验值吻合得很好,但是整体来看计算值普遍偏高,分析原因可能是由于试验时滑油是循环使用的,试验过程中轴承腔壁将会对滑油进行加热,由于很难将滑油冷却到最初的温度,在一段时间后滑油温度略有上升,冷却能力下降,导致了换热热流密度的减小。
除上述原因外,还存在其他可能因素导致换热热流密度的试验值与计算值略有不同,尤其是在滑油出口对应的测点L4=0.125 m附近出现换热热流密度的峰值,误差也相对略大,可能的原因有两方面:① 滑油在轴承腔壁面上流动时,壁面附近的滑油会发生波动现象[20];② 滑油油滴甩出以后在壁面发生的铺展、反弹、破碎、飞溅等现象同样会导致温度传感器测得的温度出现误差。
试验过程中采用热电偶丝对温度进行测试,热电偶丝为实验室自制热电偶,标定范围为15~150 ℃,在该范围内精度可达0.1 ℃,而油膜厚度的测量采用超声测量,文献[22]中对超声测量系统在不同温度条件下进行了标定,超声测量的分辨率高于0.01 mm,但是由于轴承腔表面液面的不规则会影响超声波的反射与接收,经过测试验证显示最大误差为7.1%。
总体来看,计算结果与试验结果吻合较好,能够比较真实地反应轴承腔壁面与腔内两相流场的换热特性。这也更进一步验证了计算的可靠性与准确性。
4 换热系数的影响因素
4.1 滑油油膜对局部换热系数的影响
针对本节中计算的轴承腔试验模型,根据上文计算得到的轴承腔腔内两相流流动、壁面换热参数以及试验件的几何参数,对轴承腔壁局部换热系数的关系式进行总结和分析。首先定义如下几个无量纲参数。
壁面努塞尔数Nuw为
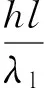
(13)
式中:λl为滑油的导热系数;l为特征长度。由于本文研究的是轴承腔内壁面上油膜与结构的换热,该内壁面直径为D2,同时转轴的旋转对换热有较大影响,转轴的直径为D1,考虑上述2个因素,式(13)中的特征长度选取腔室内外半径的平均值,即l=(D1+D2)/2,这也与Glahn的分析保持了一致[10]。
轴承腔水力直径DH为
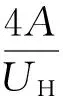
(14)
式中:A为轴承腔截面面积;UH为轴承腔截面的湿周周长。
壁面附近油膜当地雷诺数Rel为
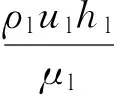
(15)
式中:ρl、ul、hl、μl分别为油膜当地的密度、速度、厚度与黏度。
转轴旋转雷诺数Rerot为

(16)
式中:rs为轴承腔当地半径;νoil为滑油运动黏度。
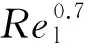
(17)

图12 壁面努赛尔数Nuw与当地雷诺数Rel的关系Fig.12 Relation between wall Nusselt number Nuw and local Reynolds number Rel
以上换热关系是针对本文的试验件数值模拟数据与试验数据分析得出。
4.2 转速对换热系数的影响
图13为滑油流量qoil=200,400 L/h时局部换热热流密度随转速的变化。从图中可以看出,沿轴向0.12~0.21 m之间的平均换热热流密度要高于0~0.12 m之间的平均换热热流密度,这可能是因为0.12~0.21 m处对应的转轴直径较大,转轴旋转时对流场的影响更加明显。
从图中结果可以看出转速也对轴承腔壁的换热有较大的影响,但是转速对局部换热的影响相对油膜的影响要复杂得多,因为转速变化过程中滑油油膜厚度与运动速度以及腔内旋转空气的转速都会发生变化,因此转速对局部换热系数的影响是多个因素复合的作用。另外,上文也显示了在同一个工作状态下,不同位置局部换热也不一致。
为了考虑转速的影响,本文在分析转速与换热系数关系的过程中初步尝试采用壁面平均换热进行计算,对相同滑油流量qoil=300 L/h下,在1 000~8 000 r/min范围内选取8个不同转速进行计算分析,得到轴承腔壁面努赛尔数Nuw与转轴旋转雷诺数Rerot之间的关系,如图14所示。由图14可以看出,lnNuw与lnRerot几乎完全符合正比例关系,由此可以得到
(18)

图13 不同转速下换热热流密度Fig.13 Heat flux density at different rotating speeds
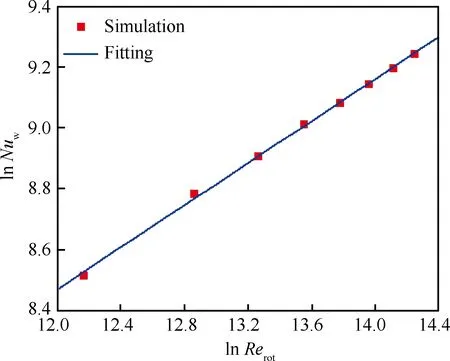
图14 壁面努赛尔数Nuw与转轴旋转雷诺数Rerot的关系Fig.14 Relation between wall Nusselt number Nuw and rotary shaft rotational Reynolds number Rerot
需要指出的是,由于对转速的计算量与试验工作量较大,式(18)的结论需要将来进一步的验证。
5 结 论
1) 对于轴承腔内壁表面的局部换热热流密度,CLSVOF数值计算与试验值在试验工况内均吻合较好。
2) 轴承腔内壁面上滑油与壁面的换热密度随转速的增大而增大,局部换热热流密度最大值出现在轴向位置0.12 m附近,这个位置处于试验件轴承腔滑油喷射出口位置。
3) 轴承腔内壁表面的油膜流动对于腔壁换热影响很大,壁面努塞尔数与滑油油膜当地雷诺数的0.7次方呈正比。
4) 壁面努塞尔数与旋转雷诺数的0.345次方呈正比,但试验及计算的转速工况有限,因此对于转速对换热的影响有待进一步研究。
[1] KLINGSPORN M. Advanced transmission and oil system concepts for modern aero-engines: GT2004-53578[R]. New York: ASME, 2004.
[2] 葛治美, 韩振兴, 张恩和, 等. 航空发动机轴承腔热分析计算[J]. 航空动力学报, 2005, 20(3): 483-486.
GE Z M, HAN Z X, ZHANG E H, et al. Thermal analysis of aeroengine bearing compartment[J]. Journal of Aerospace Power, 2005, 20(3): 483-486 (in Chinese).
[3] MICHAEL F. Analytical and numerical simulations of the two-phase flow heat transfer in the vent and scavenge pipes of the CLEAN engine demonstrator[J]. Journal of Turbomachinery, 2010, 132: 011008.
[4] GLAHN A, WITTIG S. Two-phase air/oil flow in aero engine bearing chambers: Characterization of oil film flows[J]. Journal of Engineering for Gas Turbines and Power, 1996, 118(3): 578-583.
[5] BAI C X, GOSMAN A D. Development of methodology for spray impingement simulation: SAE 950283[R]. Warrendale, PA: SAE International, 1995.
[6] FARRALL M, HIBBERD S, SIMMONS K. The effect of initial injection conditions on the oil droplet motion in a simplified bearing chamber[J]. Journal of Engineering for Gas Turbines and Power, 2008,130(1): 12501-12507.
[7] SIMMONS K. Numerical study of the two-phase air/oil flow within an aero-engine bearing chamber model using a coupled Lagrangian droplet tracking method[C]//ASME 2002 Pressure Vessels and Piping Conference. New York: ASME , 2002: 325-331.
[8] WOLFRAM K, KLAUS D, HANS J B. Influence on the oil split between the offtakes of an aero-engine bearing chamber: GT2012-69412[R]. New York: ASME, 2012.
[9] WITTIG S, GLAHN A, HIMMELSBACH J. Influence of high rotational speeds on heat transfer and oil film thickness in aero-engine bearing chambers[J]. Journal of Engineering for Gas Turbines and Power, 1994, 116(2): 395-401.
[10] GLAHN A, BUSAM S, WITTING S. Local and mean heat transfer coefficients along the internal housing walls of aero engine bearing chambers: GT1997-0261[R]. New York: ASME , 1997.
[11] BUSAM S, GLAHN A, WITTIG S. Internal bearing chamber wall heat transfer as a function of operating conditions and chamber geometry[J]. Journal of Engineering for Gas Turbines and Power, 2000, 122(2): 314-320.
[12] 陈薄, 陈国定, 王涛. 考虑油滴变形和二次油滴效应的轴承腔壁面油膜流动分析[J]. 航空学报, 2013, 34(8): 1980-1989.
CHEN B, CHEN G D, WANG T. Flow characteristics analysis of wall oil film with consideration of oil droplet deformation and secondary oil droplet deposition in aeroengine bearing chamber[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(8): 1980-1989 (in Chinese).
[13] 吕亚国, 张美华, 刘振侠, 等. 航空发动机轴承腔油气两相流流动数值研究及验证[J]. 航空动力学报, 2014, 29(11): 2751-2757.
LÜ Y G, ZHANG M H, LIU Z X, et al. Numerical study and validation for two-phase flow of oil and gas in aero-engine bearing cavity[J]. Journal of Aerospace Power, 2014, 29(11): 2751-2757 (in Chinese).
[14] CHONG Z, HU J P, LIU Z X, et al. Application of the ultrasonic oil film thickness measurement system in bearing chambers[J]. International Journal of Turo & Jet-Engines, 2013, 32(2): 159-165.
[15] 刘振侠, 黄生勤, 吕亚国, 等. 航空发动机润滑系统通用分析软件开发[J]. 航空动力学报, 2007, 22(1): 12-17.
LIU Z X, HUANG S Q, LÜ Y G, et al. General analysis software of aeroengine lubrication system design[J]. Journal of Aerospace Power, 2007, 22(1): 12-17 (in Chinese).
[16] GLAHN A, KURRECK M, WILLMANN M, et al. Feasibility study on oil droplet flow investigations inside aero engine bearing chambers—PDPA technique in combination with numerical approaches[J]. Journal of Engineering for Gas Turbines and Power, 1996, 118(4): 749-755.
[17] LIU Z X, ZHAO J Y, HU J P, et al. A numerical model for unsteady oil film motion in aero-engine bearing chamber and experimental verification: GTINDIA 2013-3639[R]. New York: ASME, 2013.
[18] CHANG Y C, HOU T Y,MERRIMAN B, et al. A level set formulation of eulerian interface capturing methods for incompressible fluid flows[J]. Journal of Computational Physics, 1996, 124(2): 449-464.
[19] CHANDRA B, SIMMONS K, PICKERING S, et al. Factors affecting oil removal from an aeroengine bearing chamber: GT2010-22631[R]. New York: ASME, 2010.
[20] ZHAO J Y, LIU Z X. Numerical and experimental study for unsteady oil film thickness of the rotating cylinder chamber wall[J]. Journal of Engineering for Gas Turbines and Power, 2015, 137(12): 122501.
[21] 任国哲, 刘振侠, 赵静宇, 等. 基于DPM与VOF方法轴承腔内滑油瞬态特性[J]. 航空计算技术, 2016, 46(1): 11-15.
REN G Z, LIU Z X, ZHAO J Y, et al. Motion of wall oil film with consideration of oil-gas coupled heat and mass transfer in bearing chamber[J]. Aeronautical Computing Technique, 2016, 46(1): 11-15 (in Chinese).
[22] 郝毓雅, 孙嘉琪, 刘振侠, 等. 轴承腔壁面液膜厚度测量系统的设计与实现[J]. 航空计算技术, 2012, 42(6): 121-124.
HAO Y Y, SUN J Q, LIU Z X, et al. Design and realization of measuring system for film thickness in bearing chamber[J]. Aeronautical Computing Technique, 2012, 42(6): 121-124 (in Chinese).
(责任编辑: 鲍亚平, 王娇)
*Corresponding author. E-mail: hujp@nwpu.edu.cn
Numerical simulation and experiment for heat transfer between oil film and inner wall of bearing chamber
HU Jianping1,*, REN Guozhe1, YI Jun2, LIU Zhenxia1, LYU Yaguo1, ZHAO Jingyu1
1.SchoolofPowerandEnergy,NorthwesternPolytechnicalUniversity,Xi’an710072,China2.AviationEquipmentDevelopmentOfficeofArmy,Beijing100021,China
It is necessary to analyze heat transfer between the lubricating oil and the inner wall of the rear bearing chamber in the design of the heat protection structure for an aero-engine. The characteristics of the influence of the inner wall heat transfer from the oil film is obtained through both experiments and numerical simulation. The temperature distribution of the outer wall, inner wall and the oil film is tested to calculate the heat flux and the transfer coefficient. The simulation of the test rig is carried out using fluid-structure coupling with heat transfer, and the CLSVOF (Coupled Level Set and Volume Of Fluid) model is adopted to simulate the gas/oil flow. Comparisons of the local heat flux are then made between the experiments and the numerical simulation under different conditions, and the results show that the simulation results agree well with the experiment data. The relation between the heat coefficient and the local oil film Reynolds numberRelis also discussed. The local Nusselt numberNuwnear the wall is directly proportional to 0.7 power of local Reynolds numberRel. In addition, analysis of the influence of the rotating speed shows thatNuwis proportional to 0.345 power of the rotary shaft rotational Reynolds numberRerot.
aero-engine; rear bearing chamber; heat transfer; lubricating oil film; experimental study; numerical simulation
2016-12-02; Revised: 2017-01-11; Accepted: 2017-03-13; Published online: 2017-05-12 10:59
URL: www.cnki.net/kcms/detail/11.1929.V.20170512.1059.006.html
s: Science Foundation of Northwestern Polytechnical University (3102015ZY090); Aeronautical Science Foundation of China (20150453004); Natural Science Foundation of Shaanxi Province (2015JQ5194)
V233.4
A
1000-6893(2017)09-521013-11
2016-12-02; 退修日期: 2017-01-11; 录用日期: 2017-03-13; 网络出版时间: 2017-05-12 10:59
www.cnki.net/kcms/detail/11.1929.V.20170512.1059.006.html
西北工业大学基础研究基金 (3102015ZY090); 航空科学基金 (20150453004); 陕西省自然科学基金 (2015JQ5194)
*通讯作者.E-mail: hujp@nwpu.edu.cn
胡剑平, 任国哲, 易军, 等. 轴承腔内壁与油膜换热的数值模拟与试验[J]. 航空学报, 2017, 38(9): 521013. HU J P, REN G Z, YI J, et al. Numerical simulation and experiment for heat transfer between oil film and inner wall of bearing chamber[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(9): 521013.
http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn
10.7527/S1000-6893.2017.621013
