远程防空导弹的新型弹道优化设计*
2017-11-20苏宪飞张忠阳张弫谷逸宇
苏宪飞,张忠阳,张弫,谷逸宇
(1.北京电子工程总体研究所,北京 100854;2.中国航天科工集团 第二研究院,北京 100854)
远程防空导弹的新型弹道优化设计*
苏宪飞1,张忠阳2,张弫1,谷逸宇1
(1.北京电子工程总体研究所,北京 100854;2.中国航天科工集团 第二研究院,北京 100854)
针对新型目标的运动学特性,在总结了传统的远程拦截导弹飞行弹道基础上,建立了快速介入拦截弹道模型并对弹道进行了仿真,并对仿真结果进行了分析。同时利用hp-自适应伪谱法以拦截时间最小为优化目标对其进行了优化。优化结果表明,快速介入拦截弹道能够很好的同时满足拦截快速性和较大横向修偏能力的需求。
远程防御;快速介入拦截弹道;hp-自适应伪谱法;弹道优化;弹道设计;高超声速
0 引言
美国HTV-2(falcon hypersonic technology vehicle 2),AHW(advanced hypersonic weapon)等新型高超声速目标采取非弹道式机动飞行方式,可在飞行过程中进行长时间、小过载、大空域的机动,并且可以中途变更打击目标,飞行弹道难以预报。其既有与弹道导弹相当的快速打击能力,同时又有空气动力类目标的长时间机动飞行能力,给防空导弹的拦截造成了很大的困难[1]。
1 弹道形式及优化问题描述
1.1弹道形式描述
远程拦截导弹飞行弹道可采用的形式有:弹道式、助推-巡航式等。
1.1.1 弹道式
弹道式是一种传统的高超声速飞行器弹道形式[2],以弹道导弹为典型代表,其弹道呈抛物线状。由于弹道导弹主要飞行在大气层外,依靠惯性以及地球引力作用长距离飞行,末端再入一般也不需要大机动,因此导弹常采用无翼正常式布局,而且弹体一般为轴对称布局。
采用纯弹道式高抛弹道,有利于减少导弹速度损失,并且导弹长时间处于50 km以上高空,可以利用星光导航修正导弹姿态误差。缺点是导弹长时间处于高空稀薄大气中,飞行末段无法利用气动力进行机动,较难对目标进行横向跟踪修偏。
1.1.2 助推-巡航式
采用助推-巡航式,导弹全程处于30~40 km高度飞行,可以利用气动力进行机动。缺点在于导弹长时间处于大气层内,速度能量损失较大;大气层内超高速飞行使得弹体表面气动加热严重,对防热设计和末制导探测带来挑战。并且若采用助推-巡航式弹道,为保持高超声速飞行,动力装置一般采用超燃冲压发动机。但是从技术成熟度和技术风险角度来看,超燃冲压发动机目前还有诸多关键技术有待攻关,将会对动力系统带来较多风险。
1.1.3 快速介入拦截弹道
综合以上2种弹道形式的优缺点以及所要拦截的目标特性,本文提出了一种名为“快速介入拦截弹道”的弹道形式。
快速介入拦截弹道兼顾以上2种弹道模式的优点。在飞行前半段,如图1中AB段所示,采用高抛式,相当于“大发射角”飞行,迅速爬升到30 km以上高空。导弹最大飞行高度可达约100 km,拦截过程大部分飞行段都在大气非常稀薄的空间做抛物线飞行,既减少导弹的速度损失,又可长时间利用星光导航修正姿态误差,也有利于解决长时间飞行气动加热问题。在飞行后半段,如图1中BC段所示,飞行高度逐渐下降到50 km以下,此时利用高气动效率机动,从而减小阻力损失,提高平均速度,而且还能有效地降低壁面热流。同时可以利用气动力修正导弹位置,并且使导弹具备较强的机动能力[3-10]。在飞行后半段,利用高气动效率机动具有3个优点:第1,机动飞行中可利用气动力不间断机动,提高了导弹自身的机动跟踪能力;第2,在机动弹道的轨迹上,导弹可实现以相对较小攻角产生较大升力,有利于减小导弹的速度损失;第3,导弹由于末段在大气层内滑翔其末速度相对于弹道式要小,相对纯弹道式弹道更有利于弹道末段对目标进行搜索巡飞。
1.2弹道优化问题描述
本文的弹道优化模式,以导弹飞行攻角作为控制量,对于铅垂面内固定的弹道命中点,形成满足目标函数、微分方程、路径约束、边界条件的优化弹道。由于本文优化的对象是远程防御弹道,所以其拦截时间不能过长,必须兼顾中程、近程等导弹的发射拦截,所以取拦截时间最短作为目标函数。导弹状态变量x为拦截弹的横向位置坐标;y为拦截弹的纵向位置坐标;v为拦截弹的速度;θ为拦截弹的弹道倾角;控制变量α为拦截弹的攻角。以上5个变量均基于发射坐标系。
1.3导弹动力学模型
本文假设拦截导弹发射点处海拔高度为0,将导弹运动看成质点运动,控制系统工作是理想的。为了使弹道优化数学模型便于实时实现,还假设导弹的发射方式是朝向预测拦截点发射,从而把导弹的三维空间运动用二维垂直平面上运动来近似,则铅垂平面内导弹运动模型可表示为
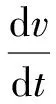
(1)
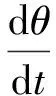
(2)
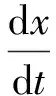
(3)
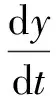
(4)

(5)

(6)

(7)
X=CX(Ma,α)qS,
(8)
Y=CY(Ma,α)qS,
(9)
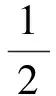
(10)
Ma=f1(v,h),
(11)
ρ=f2(h),
(12)
m=f4(t),
(13)
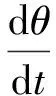
(14)
nmax=CY(Ma,αmax)qS/mg,
(15)
式中:θr为当地弹道倾角;Re为地球半径;R为飞行斜距;H为飞行海拔高度;S为导弹参考面积;ny为需用过载;nmax为可用过载。其他符号含义参见文献[11]。
2 优化方法
本文选取的弹道优化方法为hp-自适应伪谱法[12-14]。这种方法具有适应性强与收敛速度快的优点,尤其适合解决多阶段的最优控制问题。hp-自适应伪谱法的求解过程如下:
(1) 首先结合最优控制问题的物理意义将优化问题分段,本弹道优化按照导弹的飞行过程进行分段,导弹的飞行过程分为一级发动机工作段,二级发动机工作段和被动飞行段,具体时间分段区间如表1所示。
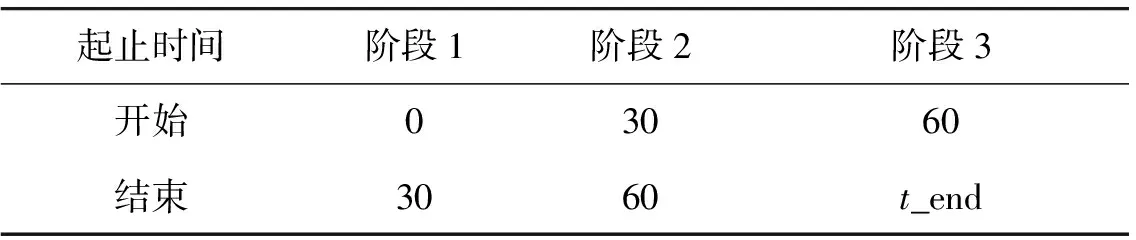
表1 导弹飞行过程分段区间表Table 1 Missile flight procedure s
(2) 在各段中选取适量的配点,并利用多项式基函数对配点和分段节点处的状态变量以及配点处的控制变量进行近似,本优化问题的状态变量x和控制变量u分别为:x=(v,θ,x,y)T,u=(α)。
(3) 将微分方程、目标函数、路径约束、边界条件按照(2)中的近似转化为代数方程。这样就把原最优控制问题转化为了NLP问题。
(4) 利用较成熟的NLP问题求解方法如序列二次规划法(SQP)等对其进行求解;
(5) 对结果进行误差分析,如不满足误差要求则自适应调整时间区间分段h以及各段近似基函数的阶次p,然后返回第一步进行迭代直到得出满足误差约束的结果。具体迭代过程如图2所示[15-16]。

图2 迭代步骤Fig.2 Iterative steps
3 弹道仿真与优化分析
3.1弹道仿真
假设导弹飞行命中点斜距1 200 km,命中点海拔高度20 km。为了实现快速介入拦截弹道的弹道形式,首先导弹垂直发射,在一级发动机和二级发动机工作段依照程序角飞行,将导弹快速送出稠密大气层,在被动飞行前段采用最大升阻比方式飞行,在弹目距离小于100 km时导弹转为比例导引,仿真步长取0.01 s。导弹飞行过程中各级发动机脉冲间隔为0。得到的导弹弹道曲线如图3所示。

图3 弹道仿真结果Fig.3 Trajectory simulation results
虚线、实线、点划线分别代表导弹飞行过程的3个阶段。从仿真结果可知,导弹飞行时间628.36 s,在第3阶段采用最大升阻比的飞行方式中导弹共跳跃2次,最终转为比例导引命中目标。仿真结果实现了快速介入拦截弹道的弹道形式,弹道曲线平滑。但是从以上仿真结果中可以看出导弹在第3阶段每跳跃一次,都造成了很大的速度损失,最终导致导弹飞行时间过长,所以有必要对以上仿真结果进行优化。
3.2拦截时间最短优化
与上节中初始条件相同,按导弹飞行过程,初始化分段时将优化问题分为3个阶段,阶段1为助推发动机工作段,阶段2为主级发动机工作段,阶段3为被动飞行段。具体分段时间区间参看表格1。计算允许误差取为10-3,各段内多项式阶次即配点数4≤p≤12,初始化时取p=5。
以平均速度最大为优化目标,即导弹飞行时间最小为目标函数进行了弹道优化,得到的优化结果如图4所示。

图4 弹道优化结果Fig.4 Trajectory optimization results
空心圆圈、三角形和菱形分别为3个阶段中自适应生成的配点,实线为根据配点拟合而成的曲线。从优化结果可知,导弹飞行时间535 s,相较于上节中的仿真结果显著降低了优化时间,得到的弹道结果平滑。从优化结果也可以看出,在第3阶段导弹仅跳跃一次,且最大高度明显降低。
3.3加入过载限制后的弹道优化
从3.2节的弹道曲线可以看出,为了达到优化目标,在飞行末端出现了弹道上抬的现象,从而导致飞行末端导弹的可用过载降低。本文设计的拦截目标航向机动性较强,为了有效拦截目标,拦截导弹在飞行过程中必须进行航向修偏,所以需对滑翔阶段导弹的可用过载进行限制。因此,本节对加入飞行末端可用过载约束的弹道进行优化。
与3.2节一致,假设导弹飞行命中点斜距1 200 km,命中点海拔高度20 km。假设导弹飞行300 s后对导弹的可用过载进行约束。因此按导弹飞行过程,优化分为4个阶段。阶段1为助推发动机工作段,阶段2为主级发动机工作段,阶段3为被动飞行前段,阶段4为被动飞行后段,此阶段要求可用过载不小于12。具体分段时间区间如表2所示。

表2 加入过载约束的弹道优化过程分段表Table 2 Trajectory optimization process with overload constraint s
其余初始化条件与3.2节相同,最终得到的优化结果如图5所示。
从优化结果可知,导弹飞行时间540 s,与上一节的优化结果相比,由于阶段4引入了可用过载的约束,导弹飞行时间更长,平均速度更低,但从以上图中可以看出,飞行300 s后弹道的跳跃程度减弱,导弹的可用过载均大于12,可见过程约束起到了作用。

图5 加入过载限制后的优化结果Fig.5 Optimization results with overload limit
4 结束语
本文针对新型高超声速目标的运动学特性,在总结了传统远程拦截弹道形式的基础上,提出了“快速介入拦截弹道”并对其进行优化。文中给出的仿真及优化结果有效满足了远程拦截弹道的拦截时间及可用过载需求。
[1] 呼卫军,周军.临近空间飞行器拦截策略与拦截武器能力分析[J].现代防御技术,2012,40(1):21-25.
HU Wei-jun,ZHOU Jun.Analysis of Near Space Vehicle Interception and Interception Weapon Capability[J].Modern Defence Technology,2012,40(1):21-25.
[2] 高洪月.弹道导弹的弹道设计与仿真[D].哈尔滨:哈尔滨工业大学,2010.
GAO Hong-yue.Trajectory Design and Simulation of Bal-listic Missile[D].Harbin:Harbin Institute of Technology,2010.
[3] 陈海兵.导弹跳跃段弹道规划与导引技术研究[D].长沙:国防科学技术大学,2006.
CHEN Hai-bing.Research on Ballistic Trajectory Planning and Guidance Technology of Missile[D].Changsha:National University of Defense Technology,2006.
[4] 郭飞帅,刘冬,张高瑜.动力滑翔导弹弹道设计[J].四川兵工学报,2011,32(7):36-39.
GUO Fei-shuai,LIU Dong,ZHANG Gao-yu.Glide Miss-ile Trajectory Design[J].Sichuan Ordnance Journal,2011,32 (7):36-39.
[5] 刘欣,杨涛.滑翔导弹再入拉起段弹道优化设计与制导[J].国防科技大学学报,2012,34(1):67-71.
LIU Xin,YANG Tao.Trajectory Optimization Design and Guidance of Reentry Stage of Glide Missile[J].Journal of National University of Defense Technology,2012,34 (1):67-71.
[6] 刘欣,李建林,葛健全,等.滑翔式飞行器再人弹道设计[J].弹箭与制导学报,2011,31(6):161-164.
LIU Xin,LI Jian-lin,GE Jian-quan,et al.Design of the Human Ballistic Missile for Gliding Aircraft[J].Journal of Projectiles and Missiles,2011,31(6):161-164.
[7] 吴了泥,黄一敏,贺成龙.基于动压剖面的再入弹道解析解[J].弹箭与制导学报,2009,29(6):173-176.
WU Le-ni,HUANG Yi-min,HE Cheng-long.Analytical Solution of Reentry Trajectory Based on Dynamic Pressure Profile[J].Journal of Projectile and Guidance,2009,29(6):173-176.
[8] 张飞天.近程弹道导弹弹道优化方法研究[D].哈尔滨:哈尔滨工业大学,2009.
ZHANG Fei-tian.Study on the Short-Range Ballistic Missile Trajectory Optimization Method[D].Harbin:Harbin Institute of Technology,2009.
[9] 张永军,夏智勋,赵建民,等.跳跃式弹道性能分析[J].弹道学报,2008,20(1):51-54.
ZHANG Yong-jun,XIA Zhi-xun,ZHAO Jian-min,et al.Performance Analysis of Jumping Trajectory[J].Chinese Journal of Ballistics,2008,20(1):51-54.
[10] 王瑞臣,洪贞启,李建林,等.主动段终点参数对弹道导弹射程的影响研究[J].青岛大学学报:工程技术版,2011,26(1):91-94.
WANG Rui-chen,HONG Qi-zhen,LI Jian-lin,et al.Stu-dy on the Influence of the Parameters of the Active Section on the Range of Ballistic Missile[J].Journal of Qiingdao University:Engineering and Technology ed,2011,26(1):91-94.
[11] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2013:1-10.
QIAN Xing-fang,LIN Rui-xiong,ZHAO Ya-nan.Missile Flight Mechanics[M].Beijing:Beijing Institute of Technology Press,2013:1-10.
[12] JAIN S,TSIOTRAS P.Trajectory Optimization Using Multiresolution Techniques[J].Journal of Guidance Control & Dynamics,2008,31(5):1424-1436.
[13] CANUTO C,HUSSAINI M Y,QUARTERONI A,et al.Spectral Methods in Fluid Dynamics[M].Springer-Verlag,1988:285-331.
[14] Benson David.A Gauss Pseudospectral Transcription for Optimal Control[J].Massachusetts Institute of Technology,2004,25(6):164-167.
[15] DARBY C L,HAGER W W,RAO A V.An hp-Adaptive Pseudo-Seudospectral Method for Solving Optimal Control Problems[J].Optimal Control Applications & Methods,2011,32(32):476-502.
[16] DARBY C L.Hp-Pseudospectral Method for Solving Continous Time Nonlinear Optimal Control Problems[D].Florida:University of Florida,2011.
NewTrajectoryOptimizationDesignofLongRangeAirDefenseMissile
SU Xian-fei1,ZHANG Zhong-yang2,ZHANG Zhen1,GU Yi-yu1
(1.Beijing Institute of Electronic System Engineering,Beijing 100854,China;2.The Second Academy of CASIC,Beijing 100854,China)
According to the kinematic characteristics of a new type of target, a kind of rapid intervention interception trajectory model is established based on summarizing the traditional long-range interception trajectory, and the trajectory simulation is carried out. Then, the trajectory simulation result is optimized using the hp-adaptive pseudospectral method to minimize the interception time. The optimization results show that the rapid intervention interception trajectory can satisfy the rapidity of interception and provide a large lateral deflection overload simultaneously.
long-range defense; rapid intervention interception trajectory; hp-adaptive pseudospectral method; trajectory optimization; trajectory design; hypersonic
2017-01-11;
2017-02-24
有
苏宪飞(1993-),男,黑龙江克山人。硕士生,主要研究方向为飞行器总体设计。
通信地址:100854 北京市海淀区永定路52号航天科工二院研究生院E-mail:1124265059@qq.com
10.3969/j.issn.1009-086x.2017.05.006
TJ761.7;V412
A
1009-086X(2017)-05-0029-06
