改进小波软硬折衷法在水下图像去噪中的应用

雷 飞，朱 林，王雪丽

(北京工业大学 信息学部，北京 100124)

改进小波软硬折衷法在水下图像去噪中的应用

雷 飞，朱 林，王雪丽

(北京工业大学 信息学部，北京 100124)

由于水在水中传播所形成的散射效应和图像传感器的成像特性会造成水下图像含有较多的噪声。因此图像去噪是处理水下图像的重要步骤。经分析，水下图像的噪声是来自图像传感器所产生的高斯噪声。为了消除水下图像噪声和增强图像细节，提出了改进小波软硬折衷算法。引入收缩因子对Donoho阈值进行改进，使小波阈值更加符合水下图像去噪的需要。之后，综合软阈值函数和硬阈值函数的特性，对软硬阈值折衷函数进行了改进，使软硬折衷函数拥有更好的数学特性。同时，该函数结构简单，计算量小，非常适合水下图像去噪对处理速度的要求。最后通过对比其他算法的均方误差、峰值信噪比和信息熵，这些数据显示该改进算法能有效地消除噪声，增强细节。

水下图像处理；图像去噪；小波软硬阈值折衷法；小波系数

0 引 言

21世纪初，人类将发展的目光转向海洋，辽阔的海洋面积是陆地面积的两倍还多，蕴含着丰富的资源，可以有效应对目前人们所面对的资源和环境的压力。但是海洋的情况相比陆地要繁杂很多，所以在开发的过程中遇到了很多困难。例如光在水中传输会被吸收，从而造成较大幅度的衰减以及散射，同时大量的海洋生物，如浮游生物及其他微小颗粒会造成水中图像信噪比降低，对比度变差，细节易模糊，整个图像会呈现出雾化的效果。所以行之有效地去除水下图像噪声、真实客观地反映出水下信息对海洋开发有着举足轻重的作用[1]。

以水下图像为研究对象，以解决图像传感器所产生的高斯噪声为主要目的。小波阈值去噪法在去除图像中的高斯噪声中应用广泛。特别是小波软阈值和硬阈值去噪法，由于其形式简单，复杂度低，增加了该方法的可用性。但是由于小波阈值的选取和硬阈值函数、软阈值函数的局限性，如硬阈值法的阈值函数具有不连续性，重构信号会产生伪吉布斯效应，而软阈值法由于小波系数总存在恒定偏差，故总是影响重构信号的真实度[2]。因此小波阈值去噪法对水下图像噪声的去噪效果并不理想。因此，针对水下图像的噪声特点，对小波软硬阈值折衷去噪法进行改进。

1 水下图像噪声分析

水下图像所产生的噪声主要来自两方面：光在水下传播形成的散射以及图像传感器形成的热噪声。

1.1光的散射形成的噪声

光在水中传输会损失能量，这是因为光在传播过程中，水作为介质会吸收光的能量。同时，水对光的吸收也有很强的选择特性。水对不同波长的光的吸收特性也是不同的。水对光谱中的紫色和红色光谱部分吸收较为严重，在可见光谱区段，吸收较为严重的是红色和淡绿色光谱部分，对蓝和深绿光谱区域吸收最少。因此，水对光的吸收使得光在传输过程中，会有部分能量的损失，这也使水下摄影、摄像变得困难[3]。

由于水对光具有一定的吸收特性，大多数水下照明系统均采用大功率强光。但是在大功率强光照明的条件下，强光在通过水中溶解物和颗粒物时增强了水的散热效应，使水的散射现象加重，在处理水下图像时需要克服这一难题。水下散射有两种主要方式：前向散射，即沿着光传输方向上的散射；后向散射，与光传输相反方向的散射。这两种散射方式导致图像模糊的原理不同，前向散射是光线从目标到达接收器传输时，光线发生小角度的偏离，使得接收光线扩散，导致水下图像模糊。后向散射发生在传感器接收光场外的光线，与场内光线叠加，形成模糊的背景，引起图像“雾化”现象，导致水下图像模糊[4]。由于此类噪声主要使图像“虚化”和“模糊”，该类噪声并不是严格意义上的图像噪声，常采用图像增强的方法来消除此类噪声。因此，此类噪声并不是文中研究的重点。

1.2图像传感器形成的噪声

通过图像传感器来获取水下视频或影像信息。图像传感器主要分为CCD(Charge Coupled Device)和CMOS(Complementary Metal Oxide Semiconductor)两大类。而这两类的成像原理都是将光信号转化为电信号，电信号会受到暗电流、电子散粒噪声和热噪声的影响，暗电流噪声、电子散粒噪声和热噪声，与成像的积分时间和图像传感器成像元件的温度成正比，并与图像传感器成像元件的温度高度相关，一般可看作高斯白噪声[5]。文中算法也是针对此类噪声。

根据噪声与图像之间的数学关系分类，主要有加性噪声和乘性噪声。图像传感器所产生的噪声—高斯白噪声，属于加性噪声。在水下图像的研究中，经常用均值为零的加性高斯白噪声(AWGN)来模拟图像噪声[6]。对于含有噪声的二维图像：

A(i,j)=A0(i,j)+N(i,j)

(1)

其中，A0(i,j)为原始图像；N(i,j)为加性噪声，其概率密度函数为：

(2)

其中，σ为噪声标准差；μ为噪声幅度的均值。

当该噪声的概率密度服从高斯分布时，其数值有70%落在[μ-2σ,μ+2σ]的范围内[7-8]，通常假设噪声幅值的均值为0。

2 改进小波软阈值去噪法

小波阈值去噪法主要是针对高斯噪声设计的[9]，适用于去除水下图像噪声的情况。因而采取其改进方法。

2.1Donoho小波阈值去噪法

Donoho等[10]提出的小波变换阈值去噪法又称为小波收缩(Wavelet Shrinkage)。其中全局阈值为：

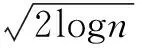
(3)

其中，n为信号长度；σ为阈值参数。

对于上述图像模型中一个尺寸为m×n的含噪图像，σ为噪声标准差，则其全局阈值为：

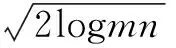
(4)

Donoho去噪方法为：

(1)对图像信号进行小波变换，得到小波系数w(f)。同时由于图片中噪声强度未知，噪声标准差近似估计为：

σ=Median(|w(f)|)/0.674 5

(5)

(2)利用硬阈值收缩函数(hard-threshold)或软阈值收缩函数(soft-threshold)进行小波变换：

①hard-threshold：

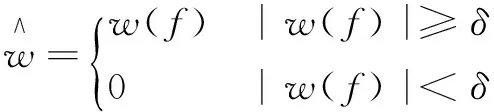
(6)

②soft-threshold：

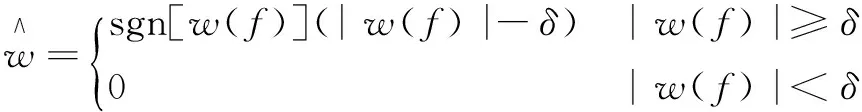
(7)

(3)进行小波反变换，重构图像。

2.2改进Donoho小波软硬阈值折衷法

2.2.1 Donoho阈值的改进

在小波变换中，阈值的选取非常重要。若阈值选取过大，根据小波变换公式，虽然去噪效果好，但也会丢失图像部分高频有用信息，使图像过于“圆滑”，造成图像的模糊。若阈值选取过小，虽然会较好地保存图像的高频信息，但去噪效果不太好，会保留过多的噪声。

全局阈值δ与图像尺寸m和n成正比，当尺寸m和n较大时，全局阈值趋于将所有小波系数置0，会使图像丢失过多的边缘信息。此时相当于使用了高通滤波器对图像进行去噪处理，从而造成图像的模糊。

相比于传统全局阈值的不足，很多情况需要引入收缩因子。邹海林[11]提出：

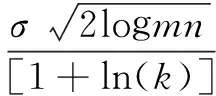
(8)

其中，k为分解尺度。

实验证明运用此阈值效果较好。但当k=1时：

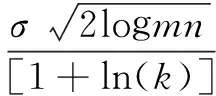
(9)

使得k=1时的情况特殊化，影响了阈值函数的数学性质。

对于上述特点，针对水下图像提出以下阈值：

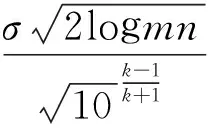
(10)

该阈值函数保证了k=1时的数学特性。且该函数针对较为模糊的水下图像的特点，去噪效果更好。k越小，全局阈值也就越大，去噪效果越好，但图像“模糊”效果、失真也越明显，所有需要选择一个合适的k。

2.2.2 软硬阈值折衷函数的改进

硬阈值函数可以保留图像边缘细节，但其数值在整个小波域内是不连续的，存在间断点，会使去噪图像发生振铃、伪吉布斯效应[12]，因此在实际运用硬阈值函数的过程中，具有一定的局限性；同时它只对小于阈值的小波系数进行处理，对大于阈值的小波系数不加处理，这与实际情况下大于阈值的小波系数中也存在噪声信号的干扰不相符。虽然软阈值法的阈值函数在小波域内是连续的，不存在间断点问题，会减少振铃、伪吉布斯效应，但软阈值对大于阈值的小波系数采取固定值压缩，这与噪声分量随着小波系数增大而逐渐减小的趋势不相符[13]。

针对软硬阈值函数的优缺点，结合水下图像的特点，赵瑞珍等[14]提出了软硬阈值折衷函数：

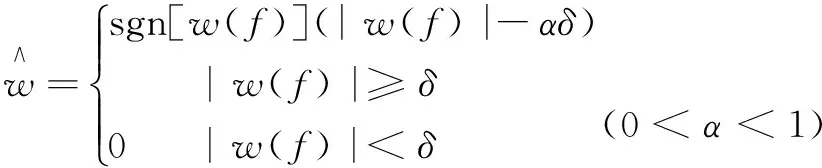
(11)

折衷函数是软阈值和硬阈值函数的结合。当α=0时，折衷函数为硬阈值函数；当α=1时，折衷函数为软阈值函数。对于0<α<1，使该函数介于软、硬函数之间。可以较好保留了图像边缘信息。同时，当w(f)与δ非常接近时，函数并不直接将小波系数置0，而是逐渐逼近为0，使得函数连续性更好。

针对水下图像，文中对软硬阈值折衷函数进行改进：

(12)

当w(f)<0时：

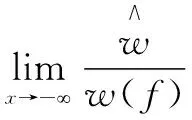
(13)

当w(f)>0时：

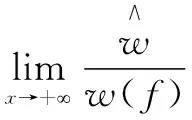
(14)

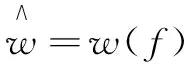
通过实验证明，在水下图像去噪处理中，α=0.5效果不错。同时，该函数结构简单，计算量小，比较适合水下图像处理对处理速度的要求。

3 实 验

3.1评价标准

图像的评价标准，主要分为主观和客观评价。主观评价是指人在一定的观测条件下直接观察图像，然后根据人眼对图像的视觉感受对图像进行评分。但主观评价容易受人为因素的影响，所以大多数图像评价标准使用客观评价的方式。客观评价是指根据仿生视觉系统建立数学模型，并通过具体的公式衡量图像的质量。客观评价标准被用来评定图像的去噪情况，提升图像边缘细节，指标包括信息熵(Entropy)、均方误差(Mean Squarer Error,MSE)和峰值信噪比(Peak Signal to Noise Ratio,PSNR)[15]。

3.2实验结果与分析

实验用一幅尺寸为700×300的水下图像，如图1(a)所示。利用Matlab 2010b进行仿真。采用文中提出的改进Donoho全局阈值和软硬阈值折衷函数。改进型Donoho全局阈值中，分解尺度k=2，软硬阈值折衷函数中α=0.5，选取sym4小波基对含噪图像进行2层分解，如图1(f)所示。与几种常用的去噪方法(中值去噪法(采样窗口为3×3)、均值去噪法(采样窗口为3×3)、小波软阈值去噪法和小波硬阈值去噪法)进行比较。

从图1(c)可以明显看出，均值滤波器针对水下图像会滤掉图像边缘细节，使图像过于模糊。

选择图像的局部区域进行对比，如图2所示。

图1 去噪图像

图2 原始图像

通过观察图3的细节照片可以看出，改进的软硬

阈值折衷算法相较于其他算法可以有效地消除水下图像的噪声，并保留图像的边缘信息。

(a)原水下图像;(b)中值滤波器的去噪图像;(c)均值滤波器的去噪图像;(d)Donoho软阈值函数的去噪图像;(e)Donoho硬阈值函数的去噪图像;(f)改进阈值函数的去噪图像

图3 局部去噪图像

表1展示了图1中各个图片的均方误差、峰值信噪比和信息熵。由表中客观评价标准可以看出，文中的改进方法在各个指标上均有提升。均值滤波器所处理的图像出现了严重的模糊，在各项指标中表现最差。

通过客观评价标准表明，文中方法拥有更高的峰值信噪比和信息熵，同时均方误差更小。不仅可以有效去除图像中的噪声，还可以增加图像中的边缘信息。

表2是选取了100张水下图像的均方误差、峰值信噪比和信息熵的平均值。从中可以看出，文中方法在各项客观标准中均取得了很好的效果。

表1 不同去噪方法的均方误差、峰值信噪比和信息熵对比

表2 100张水下图像的均方误差、峰值信噪比和信息熵的平均值

这些数据显示改进型软硬阈值折衷算法针对水下图像能有效地去除噪声，使图像更加清晰。

4 结束语

针对水下图像，提出一种改进软硬阈值折衷算法，采用了改进型阈值和改进软硬阈值折衷函数。通过仿真实验对比了传统去噪方法的均方误差、峰值信噪比和信息熵，结果表明，降低了图像均方误差，提高了峰值信噪比，该方法不仅可以有效地消除噪声，还可以增强图像的边缘信息。

[1] 蓝国宁,李 建,籍 芳.基于小波的水下图像后向散射噪声去除[J].海洋技术,2010,29(2):43-47.

[2] 颜 兵,王金鹤,赵 静.基于均值滤波和小波变换的图像去噪技术研究[J].计算机技术与发展,2011,21(2):51-53.

[3] 孙传东,陈良益.水的光学特性及其对水下成像的影响[J].应用光学,2000,21(4):39-46.

[4] 马 原.一种基于光线散射模型的水下图像增强方法[J].现代电子技术,2011,34(16):166-168.

[5] 吴 强,迟耀斌,王智勇.CCD传感器噪声对遥感影像无损压缩的影响[J].光电工程,2010,37(3):72-78.

[6] 柳 薇.SVD域的图像高斯噪声强度估计[J].中国图象图形学报,2012,17(8):923-933.

[7] 李晓飞,邱晓晖.基于小波变换的改进软阈值图像去噪算法[J].计算机技术与发展,2016,26(5):76-78.

[8] Cui H，Zhao R，Hou Y.Improved threshold denoising method based on wavelet transform[J].Physics Procedia,2012,33(1):1354-1359.

[9] Wang Q.Research on image denoising with an improved wavelet threshold algorithm[J].International Journal of Signal Processing Image Processing & Pattern Recognition,2015,8(9):257-266.

[10] Donoho D L,Johnstone I M.Ideal spatial adaptation via wavelet shrinkage[J].Biometrika,1994,12:425-455.

[11] 邹海林,隋亚莉,徐俊艳,等.基于多小波变换的GPR图象去噪方法研究[J].系统仿真学报,2005,17(4):855-858.

[12] 蒋克荣,唐向清,朱德泉.基于改进阈值小波算法的汽车轮速信号处理[J].仪器仪表学报,2010,31(4):736-740.

[13] 武文波,张 迅,陈 静.小波阈值的改进及在遥感图像去噪中的应用[J].遥感技术与应用,2007,22(6):722-726.

[14] 赵瑞珍,宋国乡,王 红.小波系数阈值估计的改进模型[J].西北工业大学学报,2001,19(4):625-628.

[15] Ghani A S G，Isa N A M.Underwater image quality enhancement through composition of dual-intensity images and Rayleigh-stretching[C]//Proceedings of fourth international conference on consumer electronics.[s.l.]:IEEE,2014.

ApplicationofImprovedCompromiseSoft-hardThresholdAlgorithminUnderwaterImageDenoising

LEI Fei，ZHU Lin，WANG Xue-li

(Faulty of Information Technology，Beijing University of Technology，Beijing 100124，China)

The quality of underwater image is poor due to the properties of camera and light transmission in water.Image denoising is an important step in underwater image processing.The kind of noise is Gaussian noise for underwater by camera through analyzing.In order to eliminate the underwater image noise and enhance the image details,an improved soft-hard threshold algorithm is proposed.First the Donoho wavelet threshold is improved by introduction of shrinkage factor that is more suitable for underwater image denoising.Then the soft-hard threshold function is modified that combines the characteristics of soft threshold and hard threshold function,which makes it with better mathematical properties,simple structure and small amount of calculation that is very suitable for processing speed requirements of underwater image denoising.Finally,compared with other algorithms on mean square error,peak signal to noise ratio and entropy,it is showed that it can successfully reduce the noise and increase the details.

underwater image processing;image denoising;wavelet soft-hard threshold;wavelet coefficient

2016-10-17

2017-01-17 < class="emphasis_bold">网络出版时间

时间：2017-07-19

国家自然科学基金资助项目(61533002)

雷 飞(1972-)，男，博士，副教授，研究方向为图像处理、计算机智能控制系统。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170719.1108.018.html

TP39

A

1673-629X(2017)11-0150-04

10.3969/j.issn.1673-629X.2017.11.033