一种地空3D-Massive MIMO信道模型

王鑫， 张晓林， 曹晏波

1.北京航空航天大学 电子信息工程学院， 北京 100083 2.大唐电信科技产业集团， 北京 100191

一种地空3D-Massive MIMO信道模型

王鑫1,*， 张晓林1， 曹晏波2

1.北京航空航天大学 电子信息工程学院， 北京 100083 2.大唐电信科技产业集团， 北京 100191

为了研究地空3D-Massive MIMO系统信道特性，提出一种基于三维单跳同心圆环散射体的地空3D-Massive MIMO信道模型。相比传统地空3D MIMO信道模型有两方面改进，首先是建立了基于单跳圆环散射体3D几何精确位置关系的球面波天线阵元相位偏移模型，其次采用生灭过程对Massive MIMO阵列上的非平稳特性进行建模。推导了该模型的信道统计特征函数，通过对特征函数理论推导值与蒙特卡洛统计值进行仿真对比，验证了理论推导正确性。此外，对所提信道模型与基于平面波的传统地空3D MIMO信道模型的空间相关性进行了分析及仿真对比，结果表明：在远场环境下，两者基本一致；在近场环境下，传统平面波模型不再适用，两者存在差异。最后，对若干组表征信道特征的仿真结果与公开文献中地空信道实际测试数据进行对比分析。表明本模型作为普遍适用性模型，可以根据信道的测试条件、测试环境和测试结果来优化参数配置以趋近于实际信道，以对特定信道进行精确建模。

信道模型； Massive MIMO； 信道统计特征函数； 非平稳特性； 同心圆环散射体； 远场模型

由于Massive MIMO[1]技术极大的增加了频谱利用率，因此在工业界和学术界均获得了高度的关注，现已成为5G系统的MIMO增强技术。Massive MIMO技术是指放置远多于现今系统中所使用的天线数量的一种天线架设模式，比如使用几十或者上百根基站天线来同时服务一定数量的用户终端。相对于传统的MIMO系统，大规模MIMO系统呈现出一些全新的特性。在大规模MIMO系统中，原本随机分布的信道矩阵渐趋确定，小尺度衰落效应被有效平均。根据大数定理，当发射天线数远远大于终端用户数时，不同用户间的信道向量呈现渐近正交的特性[2-3]。

将Massive MIMO应用于地空通信中，可将能量高度集中在飞机用户方向从而提升信号接收灵敏度，提高抗干扰能力。此外，相比于传统MIMO，具备更大的空间自由度，使得地空信道容量得到成倍提升[4]。

为了设计和评估地空Massive MIMO系统方案以及性能，必须对小尺度衰落信道进行建模。关于MIMO信道模型，基于几何的物理信道模型(Geometry based Stochastic Channel Model，GSCM)被广泛采用，比如单环、双环、椭圆模型[5]，以及SCM[6]，WINNERⅡ[7]以及IMT-Advanced[8]等。对于航空通信的传统3D MIMO信道，文献[9]建立了地空下行单跳同心椭圆环MIMO模型，并对机载MIMO天线间隔以及圆阵、线阵布局方式的信道容量进行了分析。文献[10-12]建立了航空信道下的三维单跳同心圆环散射(Geometrically-Based Single-Bounce Concentric-Cylinders Scattering,GBSBCCS)模型,认为飞机远高于地面站，地面站通常处于较开阔地带，高山、建筑等散射体以地面站为中心呈四周分布，地面站的高度要远低于散射体的高度，建立一跳圆环模型是合理的且与实测结果相吻合[13]。

文献[14-16]对地面Massive MIMO移动通信系统进行了信道建模，并指出传统MIMO信道模型并不能直接应用于Massive MIMO信道场景中，相比于传统MIMO信道，Massive MIMO信道有两个重要区别：

1) 在传统的MIMO通信系统中，一般认为，到达天线阵列处的波为平面波。但是，对于Massive MIMO天线阵列，由于天线尺寸可能超过电波波长数10倍，特别当天线与散射体之间，或者收发天线距离较近时，到达Massive MIMO天线阵列的不同阵元上的电波会呈现球面波特性。因此，需要结合天线与信号源的几何关系确定传播模型。

2) 由于Massive MIMO阵列尺寸大，一些散射体不是对整个阵列可见的，同样的散射体对某些阵元是可见的，但同时对其他阵元是非可见的。这就意味着在建模时要考虑模拟一个散射体可见区域。所以，传统的MIMO阵列上的平稳特性不再适用。

对于第2个因素，文献[14-15]采用泊松过程建模，认为散射体在相邻阵元间是否可见满足生灭过程，文献[16]采用了球体模型建模，当散射体与目标阵元的距离小于球体半径时才认为可见。

本文建立了基于单跳圆环散射体的地空3D-Massive MIMO模型。相比传统地空3D MIMO信道模型的改进在于，建立了基于单跳圆环3D精确几何位置关系的球面波天线间信道响应模型，并采用生灭过程对Massive MIMO阵列上的非平稳特性进行建模。

文章结构如下：第1节提出地空3D-Massive MIMO信道模型；第2节推导了该模型的信道统计特性函数值；第3节给出仿真及结果分析；第4节对全文进行总结。

1 系统模型

地空3D-Massive MIMO单跳圆环模型如图1 所示。定义x-y平面为包含地面站高度Hg的切面圆, 并以地面站天线中点γga为圆心；选择飞机天线中点为Oa，Oa在x-y平面的投影为O, 连接O-Og作为x轴, 连接天线O-Oa作为z轴。

模型设定地面站固定，天线阵列架设高度为Hg，被半径为Rc、高度为Hc的圆筒状散射体包围。地面站天线阵列的方位角与俯仰角分别为αg、γg，天线间距为δg，阵型为线阵，天线个数为

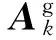
地空信道包含直射、反射与散射3种分量[8]。地面站第k根天线到飞机处第r根天线的地空信道3D-Massive MIMO的信道响应可表示为

(1)

为方便分析又不失一般性，做出以下假设：

1) 飞机和地面站均安装线形天线阵列，由于地面站有足够大的天线安装空间，因此模型假设地面站安装Massive MIMO天线阵列。考虑到飞机天线安装空间相对较小，设定飞机天线阵列阵元Ma≪Mg，实际情况中，本文的模型理论上不对Ma的大小进行限制。

2) 对于同一个散射体n带来的S条多径，其中每条不可分辨径l到达天线阵列的时延τn,dif,l均相同，即τn,dif,l=τn,dif,S=τn,dif。

3) 飞机与地面站距离、飞机飞行高度以及地面站高度远大于天线间距，满足条件：Dga≫max(δa,δg)，Ha≫max(δa,δg)，Hg≫max(δa,δg)。

1.1 散射分量传播模型

由于散射体存在于地面站周围，因此建模为单跳模型，且散射体均匀分布在圆筒上，圆筒的高度Hc以及半径Rc决定了最大时延。假设共有N个散射体。根据地面站阵列中心到散射体n的第l条子径的离开方位角αg,n,l、俯仰角γg,n,l，由向量知识计算得到地面站以及飞机处天线阵列经第l条子径到达散射体n的距离向量分别为

(2)

(3)

建模时，选择Von-Mises函数[11，17]作为αg,n,l(t)的概率密度函数pα(αg,n,l)，选择复合函数[9，11]作为γg,n,l(t)的概率密度函数pγ(γg,n,l)。

飞机天线经散射体n到达地面天线的时延可表示为

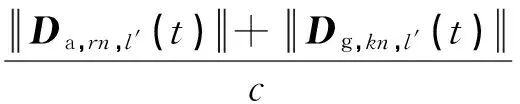
(4)

式中：c为光速；第l′条子径代表中径，中径的到达角(离开角)等于所有子径的平均到达角(离开角)。

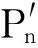
(5)

式中：τmax为最大时延；τslope为常数，决定了功率变化的快慢。

经过散射体n的信道响应表示为

(6)

而对于传统地空3D-MIMO模型，则认为散射体符合远场条件，即不同天线r的多普勒频移相等：

1.2 直射以及折射分量传播模型

第k根地面天线到第r根飞机天线直射分量的方向向量表示为

(7)

其信道时延以及信道响应分别表示为

(8)

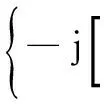
(9)

反射分量往往伴随着直射分量，且与直射分量在同一铅垂面上，如图2所示。

根据镜面反射定理可以确定飞机处第r根天线到第k根地面天线的反射路径长度为

(10)

式中：

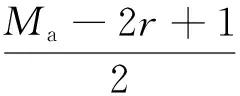
则折射径时延为

(11)

折射径信道响应为

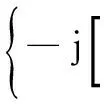
(12)

传统地空MIMO模型中，有

式中：Da,k,spe(t)为折射点到飞机阵列中心点的向量。

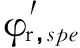
1.3 天线阵列非平稳特性建模

在Massive MIMO模型中，天线阵列轴上的散射体对某些天线阵元是可见的，但对其他一些阵元是非可见的，参考文献[16，19-20]，本文将生灭过程引入以建模地空模型Massive MIMO阵列上的非平稳特性。需要说明的是，由于本文模型中散射体只存在于地面站周围，因此，只对地面站Massive MIMO阵列建立非平稳特性。

假设在空间上散射体的生成速率为λB/m，消亡速率为λD/m。则一个散射体在相邻阵元间隔δB上的生成概率和在间隔δD消亡的概率均满足指数分布。

则平均每阵元的散射体数量为

(13)

从天线k-1到天线k的间隔δg上，散射体生存的概率为

(14)

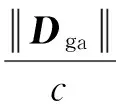
式中：因子Dg反映了散射体在阵元轴上相邻天线间的相关性，可见，Dg值越大，散射体在天线间的生存概率越大。

假设对于某个散射体，一旦消亡便不再出现，即某个散射体只可能在相邻的若干根天线上可见，则每个天线阵元上新增散射体的数量为

(15)

而传统地空3D MIMO模型中，认为每个天线阵元上对所有N个散射体均可见。

2 信道统计特性

为了研究地空3D-Massive MIMO信道特性，需要推导信道统计函数，包括空间互相关函数，时间自相关函数以及多普勒谱密度函数。此外，本文还定义了天线阵列入射角偏差均方根函数，以刻画球面波在不同Massive MIMO阵元上的入射角偏差程度。

1) 空间互相关函数

直射径、反射径以及散射径互不相关，因此，信道的空时相关函数理论表达式为

(16)

当考察阵列空间相关性时，不考虑其时间相关性，因此，Δt=0时，各分量空间互相关函数理论值分别表示为

直射分量：

PLOSe-j(φk′r′,los-φkr,los)

(17)

反射分量：

PSPEe-j(φk′r′,spe-φkr,spe)

(18)

散射分量：

pα(αg,n,l)pγ(γg,n,l)dαdγ

(19)

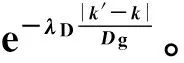
实际在建模过程中，当子径数S太大，将带来很大的信道生成计算复杂度。因此，S的大小需要在统计精度和复杂度之间进行权衡。当S取有限值时，空间互相关函数的蒙特卡罗统计值为

(20)

2) 时间相关函数

时间相关函数统计某一对收发天线在不同时刻的信道互相关值。当k=k′，r=r′时，时间自相关函数的理论值分别为

直射分量：

PLOSe-j2πΔtfrk,los

(21)

反射分量：

PSPEe-j2πΔtfrk,spe

(22)

散射分量：

(23)

散射分量的时间自相关函数的蒙特卡罗统计值为

(24)

对于传统的地空3D MIMO信道，时间自相关函数表达式与式(22)～式(24)类似，需替换f′→f。

3) 频率密度函数

频率密度函数为时间自相关函数的傅里叶变化：

(25)

4) 天线阵列入射角(离开角)偏差均方根

(26)

θg,n,l(k)=arccos[〈Dg,n,l(t),

(27)

(28)

(29)

3 仿真结果

3.1 地空3D-Massive MIMO信道统计特性仿真

本节对本文模型的信道统计特性进行仿真，通过对信道统计函数的理论推导值与蒙特卡罗统计值进行对比，以评判理论值的正确性；同时，选取并评估合适的S值，使得统计值与理论值差异足够小。由于散射径的相关函数理论值表达式较复杂，很难得到闭式解，所以理论值通过MATLAB数值积分进行估算。

在本节仿真结果图中，如无特殊说明，仿真参数如下。波长λ=0.15 m，地面站相关参数为：高度为Hg=5 m，阵列天线个数Mg=64，天线间距δg=0.5λ，地面站天线方位角与俯仰角分别为αg=0.261 8 rad，γg=0.052 4 rad，阵列天线中心处的平均离开方位角与俯仰角分别为αg,1,l′=0.977 9 rad，γg,1,l′=0.061 2 rad；飞机处相关参数为：飞机高度为Ha=6 000 m，阵列天线个数Ma=2，天线间距δa=0.5λ，飞机处天线方位角与俯仰角分别为αa=0.174 5 rad，γa=0.261 8 rad，地面站与飞机间在x轴上的水平距离Dga=10 000 m，最大多普勒频移fmax=1 815 Hz；散射体圆筒高度为Hc=200 m，半径为Rc=800 m； Von-Mises函数中控制扩展控制参数η=10，符合函数中参数m1=0，n1=0，A=2,B=18.2，C=12；泊松过程中参数Dc=1， 生存速率λB=4/m，消亡速率λD=2/m，散射体个数N=30。

1) 空间相关性

图3～图7分别对不同序号天线间的空间相关性、不同天线间距下的空间相关性以及天线不同摆放角度下的空间相关性进行仿真。

地面站天线1与天线k之间的空间相关函数绝对值如图3所示，两者的相关值随着天线序号k的增加而减小。对于同一天线序号k，当考虑散射体在阵列上的非平稳特性时，相比不考虑非平稳特性时有更小的相关值。此外，当S=200时，相比S=100更加接近于理论值。从仿真结果可见，理论值与统计值基本一致。

图4分别给出了地面站、飞机阵列空间相关性与天线间距之间的关系。

可以看出，无论是在地面站还是飞机天线阵列处，空间相关性均随着天线间距增大而减小。对于飞机天线阵列，与地面站天线阵列相比要达到同样的相关值需要更大的天线间距，是因为飞机与散射体距离很远，导致散射体子径到飞机天线阵列的角度扩展较小。从仿真中可以看到，当飞机与地面站之间的距离由10 000 m 减小到4 000 m后，空间相关性减小，因为当距离减小后飞机阵列处到达角度扩展相应增加。

图5分别给出了地面站、飞机阵列相关性与天线摆放角度之间的关系。可见，无论是在地面站还是飞机天线阵列处，空间相关性均随着天线方位角以及俯仰角的变化而变化，存在最大值以及最小值。当η变大时，到达方位角角度扩展值减小，因此空间相关性相应增加。

2) 时间相关性及频率谱密度

图6分别给出了散射体1上多径的时间自相关函数绝对值和多径的归一化频率谱密度绝对值。

当fmax=1 815 Hz时，根据仿真设置中径到达角参数αg,1,l′、γg,1,l′可计算出平均多普勒频率为1 170.8 Hz，对应仿真中峰值位置。

3) 离开角偏差均方根

图7给出了地面站阵列处由散射体1多径带来的入射角度偏差均方根统计值。由仿真结果可见，角度偏差随着天线数增大而增加，当天线个数较小时此偏差可忽略，但当天线数较大时此偏差变得不可忽略。当散射体圆筒半径Rc=800 m变为Rc=400 m时，由于散射体与阵列距离减小，角度偏差均方根进一步增加。而传统3D MIMO信道模型中，入射角偏差为0。

4) 非平稳特性

图8给出了地面站不同天线k上对应的散射体编号。

可见，对于同一个散射体，消亡后便不再出现，且当两根天线相距越远，同一个散射体在这两根天线上同时可见的概率越小。

3.2 地空 Massive MIMO与传统地空3D MIMO模型空间相关性比较

图9和图10对比了本文模型与传统3D MIMO模型空间相关性的区别。横坐标θ表示中径在Massive MIMO阵列上的离开角。仿真结果表明，当散射体距离Massive MIMO阵列较远时(Rc=500 m)，传统3D MIMO的远场模型相关值与本文模型相关值一致，而当散射体离阵列较近时(Rc=50 m)，近场模型不可忽略，此时两者相关性有较大差异。对于传统模型，相关性不会随着散射体距离变化而变化，且相关性关于θ=π/2对称，并在θ=π/2处达到最小；在近场情形下，本模型反映了近场特性，其相关性并无对称性质，且在一定的离开角范围内，相比传统模型空间相关性相比偏大，如取图10中θ=5π/6时。可见，本文的基于精确3D几何位置关系的Massive MIMO模型较传统3D MIMO模型，兼顾了近场情形。

3.3 本模型与实际测试数据的对比验证

本文模型为普遍适用性模型，相关参数可根据信道环境进行配置和调整。对于特定的信道环境，模型可根据测试条件、测试环境和测试结果来确定参数配置以优化该信道的建模，以下给出本文5种表征信道特征值的仿真结果与公开文献中地空信道实际测试数据的对比分析。

1) 近场条件球面波空间相关性对比分析

美国空军研究实验室(AFRL)于2011年在美国纽约北部进行了地空MIMO信道模型的测量实验[21]。所用频点为f=915 MHz，无人机上搭载天线个数为Ma=2，天线间距为δa=2λ，飞行高度约为Ha=200 m，飞行半径约为D=180 m。地面站MIMO测试设备置于测试车上，天线个数Mg=8。文中定义两天线间相关性采用艾尔米特角(Hermitian Angle)表示为

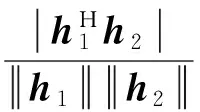
(30)

式中：h2=[hkrh(k+1)r],k=1,2，…,7，hkr为地面天线k到飞机天线r的信道响应；h1=[h4rh5r]。式(30)表征了天线对{4 ,5}与天线对{k,k+1},k=1,2，…,7的空间相关性。

文献[21]由测试环境的几何关系分析后，认为信道建模为直射径与单散射径的叠加：

(31)

式中：θv为直射径到达地面MIMO阵列的入射角；d为地面MIMO天线间距；rsk为散射体到第k根天线的距离；α为散射径功率归一化因子；φs为散射体初始相位。

文献[21]指出，此散射径来源于车顶篷，由于车顶与天线阵距离在菲涅尔区域内，因此来波为球面波，建模如图11所示，并且测试了两种测试环境下的天线相关性，其艾尔米特角表征的相关性如图12(a)，横坐标代表天线对序号，纵坐标cosθH代表天线对间艾尔米特角。

式(31)中待定参数集合U={θ,rsk,α,φs}的元素值可根据式(30)结果与实际测试数据按均方误差最小化准则得到：

(32)

式中：rsk由散射体位置坐标确定。通过对集合U中参数的多维联合搜索，文献[21]得到了各参数的取值：

测试环境1：飞机直射径入射角度θ=1.5 rad，散射体位置为：x=2.3λ，y=0.5λ。

测试环境2：飞机直射径入射角度θ=1.64 rad，散射体位置为：x=2.2λ，y=1.3λ。

对于本模型，虽然并没有在建模过程中考虑测试车顶蓬带来的散射，但是仍可以将车顶蓬建模为圆桶散射体上的一点，以测试环境1为例，对应模型中参数配置如下：飞机高度Ha=200 m，地面站高度Hg=2 m，地面站与飞机距离Dga=200.5 m，地面站与飞机间连线向量的方位角为αga(t)=π，飞机天线阵方位角与俯仰角分别为αa=0 rad，γa=0 rad，地面站天线阵列方位角为俯仰角分别为αg=0 rad，γg=0 rad。以上参数可保证飞机天线发送入射角与地面阵列夹角约为θ=1.5。设置波长为λ=300/915 m，散射体圆筒高度为Hc=2.066 m，散射体半径为Rc=0.016 4 m，则散射体的方位角与俯仰角分别为αg,n,l′=0 rad，γg,n,l′=1.471 1 rad，以上参数可保证散射体位置在水平方向上对应于图11中位置x=2.3λ，在垂直方向上对应于图中y=0.5λ。散射径只取中径，S=1。依式(32)计算仿真后，取初始相位φs=1.319 5 rad。

模型按以上参数配置后得到hk值，按式(30)可求得cosθH。测试环境2的求法同测试环境1，本文模型仿真得到的两组测试环境下的艾尔米特角结果如图12(b)所示。

图12的结果表明，本模型通过实际测试数据来配置相应参数从而生成该信道下的信道响应，使得近场球面波条件下天线空间相关性与实测结果较好的吻合，因此本文模型可支持近场条件的球面波模型建模。

2) Massive MIMO信道容量的对比分析

在文献[22]中，对Massive MIMO系统的信道容量进行了实际测量，所用频点为f=2.6 GHz，基站配置128 Massive MIMO，并架设于兰德大学工程学院的E-building楼顶上，在地面上选取8个测试点放置单天线终端进行信道测量。楼顶距地面较高，有直射径存在。由于基站架设高度高，因此测试环境可以作为地空Massive MIMO信道的一个近似模拟，测试数据对地空Massive MIMO有重要参考作用。

Massive MIMO的信道容量定义为

(33)

式中：hkr为K×M的信道矩阵，元素hkr代表第k根发射天线到第r根接收天线间的信道冲击响应。文献中基站发射天线个数K=128，终端个数M=4。作者给出了在MS2处的信道容量CDPC分别在均匀线型阵列(Uniform Linear Array,ULA)以及均匀圆型阵列(Uniform Circular Array,UCA)下的测量值，并与信道为独立同分布瑞利衰落信道的理论容量进行了对比，如图13(a)所示。

对于本文模型，设置地面站天线数Mg=128，为模拟4个用户，设置分机阵列天线个数Ma=4，设置天线间距足够远δa=50λ，以保证低相关。其他参数设置同4.1节。将式(6)生成的散射径信道代入式(33)中并进行统计，得到不同Massive MIMO天线个数的信道容量仿真结果如图13(b)所示，并将理想独立同分布瑞利衰落信道的理论容量进行对比。

本文模型仿真结果表明,随着Massive MIMO天线个数的增加，信道容量的增长趋缓，且在天线个数为128时，CDPC达到13.5 bit·s-1/Hz与理想CDPC有不到1 bit·s-1/Hz的差距。结果与实际测量结果基本吻合。

3) 散射径幅值分布概率密度对比分析

文献[23]中讨论了在L波段以及S波段航空信道特性测试结果，测试地点位于加利福尼亚爱德华兹空军基地。测试表明该处航空信道由一条直射径以及两条散射径组成。并且测试结果表明，散射径实部与虚部服从高斯特性，且方差约为σ2=1.637×10-3，如图14(a)所示。

4) 时延功率谱对比分析

同样在文献[23]中，飞机在Cords road上飞行高度为5 000英尺即1 524 m，测得的多径功率时延谱如图15(a)所示，观察到最大时延约为333 ns。

对于本模型的适配，设置飞机高度Ha=1.5 km，地面站高度Hg=2 m，地面站与飞机距离Dga=100 km，散射体圆筒高度为Hc=5 m，散射体半径为Rc=78 m，散射体个数为N=21，根据地面站高度、散射体圆筒半径和高度得到散射体方位角αg,n,l′在[-π,π]之间分布，俯仰角γg,n,l′在[-0.256 0,0.038 4] rad之间分布。根据式(4)，可得到不同位置散射体的相对时延值如图16 所示。

根据测试到的最大时延可确定第n个散射体的相对时延为

(34)

由此可根据式(4)、式(34)及图15中结果来确定时延为τn的第n个散射体的方位角αg,n,l′与俯仰角γg,n,l′，并由各时延对应的功率值实测结果来确定第n条散射径功率Pn。最终从本模型仿真得到的在333 ns以内的时延功率谱结果如图15(b)所示。仿真得到的功率谱仿真结果与实际数据结果基本吻合。

5) 频率谱密度对比分析

文献[24]给出了C波段地空信道的时延谱和多普勒谱测试结果，飞机与地面站距离最大为Dga=400 km。飞机为发射端且装有两根发射天线，在飞行模式下，抓取到的数据表明只存在直射径，图17(a)中时延谱的两条径由两根发送天线的相对发射时延导致。使用频点为f=5.1 GHz，飞行速度为v=340 m/s，理论最大多普勒频移为fmax=5 800 Hz，采集到的频率谱密度峰值所在位置为4 053 Hz。

在本文模型中，设置移动速度为va=340 km/h，飞机高度Ha=6 km，地面站高度Hg=2 m，地面站与飞机距离Dga=400 km，飞机天线阵方位角与俯仰角分别为αa=0.8 rad，γa=0 rad，地面站天线阵列方位角为俯仰角分别为αg=0，γg=0 rad。此时可得直射径的多普勒频移约为4 052 Hz，得到的频率谱密度绝对值如图17(b)所示。本模型经过合理参数配置后，频率谱密度仿真结果与实际数据结果基本吻合。

4 结 论

1) 建立了单跳散射体圆筒与天线阵列位置精确3D几何关系的具有近场球面波特性的阵列信道响应。

2) 引入生灭过程体现地面站Massive MIMO天线阵列上的非平稳特性。

通过仿真与分析得到结论如下：

1) 信道统计函数的理论推导值在不同信道场景下与蒙特卡罗统计值基本吻合，证明了理论推导函数的正确性，同时也表明在建模过程中取子径数S=200是合理的。

2) 当散射体与Massive MIMO阵列距离较远时，本文的基于单跳圆环3D精确几何位置关系的模型与传统地空MIMO远场模型相关性一致；当散射体与Massive MIMO阵列距离较近时，近场效应不可忽略，此时两个模型的空间相关性并不相同，本模型兼顾了近场情形。

3) Massive MIMO阵列在非平稳特性空间相关性要小于平稳特性，可根据实际信道环境通过调整参数λB以及λD控制非平稳特性下天线相关性大小。

最后本文对近场环境空间相关性、Massive MIMO信道容量、散射径幅值分布概率密度、时延功率谱、频率谱密度等5组表征信道特征的仿真结果与公开文献中地空信道实际测试数据进行对比分析，表明本模型作为普遍适用性模型，可以根据信道的测试条件、测试环境和测试结果来优化参数配置以趋近于实际信道，以对特定信道进行精确建模。

本文构建的理论地空3D Massive MIMO模型可为后续的地空Massive MIMO方案研究与设计提供参考。

[1] MARZETTA T L. Noncooperative cellular wireless with unlimited numbers of base station antennas[J]. IEEE Transactions on Wireless Communications， 2010， 9(11): 3590-3600.

[2] MATTHAIOU M, MCKAY M R, SMITH P J, et al. On the condition number distribution of complex Wishart matrices[J]. Transactions on Wireless Communications， 2010， 58(6): 1705-1717．

[3] RUSEK F， PERSSON D， LAU B K. Scaling up MIMO: Opportunities and challenges with very large arrays[J]. IEEE Signal Processing Magazine, 2012, 30(1): 40-60.

[4] 刘留, 陶成, 卢艳萍, 等. 大规模多天线无线信道及容量特性研究[J]. 北京交通大学学报, 2015, 39(2): 69-79. LIU L, TAO C, LU Y P, et al. Research on the propagation condition and channel capacity for massive MIMO[J]. Journal of Beijing Jiaotong University, 2015, 39(2): 69-79 (in Chinese).

[5] LIBERTI J C, RAPPAPORT T S. A geometrically based model for line-of-sight multipath radio channels[C] //46th Vehicular Technology Conference. Piscataway, NJ: IEEE Press, 1996: 844-848.

[6] 3GPP. Spatial channel model for multiple input multiple output(MIMO)simulations(Release:10)：TR 25.996 V10.0.0[S]. Sophia Antipolis: 3GPP, 2011.

[7] KYOSTI P. WINNER II channel models, Sep. 2007, WINNER D1.1.2 ver1.1. [EB/OL]. (2007-11-30)[2016-05-25].http://www.ist-winner.org/WINNER2-Deliverables/D1.1.2v1.1.pdf.

[8] ITU-R. Guidelines for evaluation of radio interface technologies for IMT advanced: Report ITU-R M.2135-1[R]. Geneva: ITU-R, 2009.

[9] 陈自力, 高喜俊. 阵列布局对机载MIMO信道容量影响[J]. 信号处理, 2015, 31(6): 686-693. CHEN Z L, GAO X J. The effect of array structures on airborne MIMO channel capacity[J]. Journal of signal processing, 2015, 31(6): 686-693 (in Chinese).

[10] 胡永江, 李小民. 基于非全向天线的无人机MIMO信道模型研究[J]. 航空学报, 2011, 32(6): 1092-1101. HU Y J, LI X M. Investigation on MIMO wideband and channel model for unmanned aerial vehicle with non-unidirectional antennas[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(6): 1092-1101 (in Chinese).

[11] 胡永江, 李小民. 一种三维无人机MIMO宽带信道模型[J]. 军械工程学院学报, 2012, 24(6): 50-55. HU Y J, LI X M. A Three-dimensional MIMO wideband channel model for the unmanned aerial vehicle[J]. Journal of Ordnance Engineering College， 2012, 24(6):50-55 (in Chinese).

[12] 李璞， 高喜俊， 陈自力, 等. 一种基于无人机MIMO信道的容量分析方法[J]. 测控遥感与导航定位, 2013, 43(2): 42-45. LI P, GAO X J, CHEN Z L, et al. Method of capacity analysis based on unmanned aerial vehicle MIMO channel[J]. Radio Engineering of China, 2013, 43(2): 42-45 (in Chinese).

[13] QU S, YEP T. A three-dimensional scattering model for fading channels in land mobile environment[J]. IEEE Transactions on Vehicular Technology, 1999, 48(5): 765-781.

[14] SHANG B W, CHENG X W, AGGOUNE HME. A non-stationary 3-D wideband twin-cluster model for 5G massive MIMO channels[J]. IEEE Journal on Selected Areas in Communications, 2014,32(6): 1207-1218.

[15] SHANG B W, CHENG X W, HAAS H. A non-stationary wideband channel model for massive MIMO communication systems[J]. IEEE Transactions on Wireless Communications, 2015,14(3): 1434-1446.

[16] XIE Y, LI B, ZUO X Y, et al. 3D geometry-based stochastic model for 5G massive MIMO channels[C] //11th EAI International conference on Heterogeneous networking for quality, Reliability, Security and Robustness(QSHINE 2015). Piscataway, NJ: IEEE Press, 2015: 216-222.

[17] HAAS E. Aeronautical channel modelling[J]. IEEE Transactions on Vehicular Technology, 2002, 51(2): 254-264.

[18] ABDI A, BARGER J A, KAVEH M A. Parametric model for the distribution of the angle of arrival and the associated correlation function and power spectrum at the mobile station[J]. IEEE Transactions on Vehicular Technology, 2002, 51(3): 425-434.

[19] ZWICK T, FISCHER C, DIDASCALOU D W, et al. A stochastic spatial channel model based on wave-propagation modelling[J]. IEEE Journal on Selected Areas in Communications, 2000, 18(1): 6-15.

[20] ZWICK T, FISCHER C, WIESBECK W. A stochastic multipath channel model including path directions for indoor environments[J]. IEEE Journal on Selected Areas in Communications, 2002, 20(6): 1178-1192.

[21] WILLINK T J, SQUIRES C C, COLMAN G W K. Measurement and characterization of low-Altitude air-to-ground MIMO channels[J]. IEEE Transactions on Vehicular Technology, 2016, 65(4): 2637-2648.

[22] GAO X, EDFORS O, RUSEK F. Massive MIMO performance evaluation based on measured propagation data[J]. IEEE Transactions on Wireless Communications, 2015, 14(7): 3899-3910.

[23] RICE M A. Multipath channel model for wideband aeronautical telemetry[C]//2002 Military Communication(MILCOM). Piscataway, NJ: IEEE Press, 2002: 622-626.

[24] BLUEMM C, HELLER C, FOURESTIE B. Wideband aeronautical channel sounding and modeling for C-band telemetry[C]//2013 Personal Indoor and Mobile Radio Communications(PIMRC). Piscataway, NJ: IEEE Press, 2013: 264-269.

(责任编辑：苏磊)

URL：www.cnki.net/kcms/detail/11.1929.V.20161110.1418.005.html

＊Corresponding author. E-mail: sportxin_558@163.com

A 3D-Massive MIMO ground-air channel model

WANG Xin1,*, ZHANG Xiaolin1, CAO Yanbo2

1.SchoolofElectronicsandInformationEngineering,BeihangUniversity,Beijing100083,China2.DatangTelecomTechnology&IndustryGroup,Beijing100191,China

In order to analyze the channel characteristic of ground-air 3D-Massive MIMO system，this paper has presented a ground-air 3D-Massive MIMO channel model of geometrically-based single-bounce concentric-cylinders scattering. Compared with traditional ground-air 3D MIMO channel model, the proposed model has two improvements. First, a model for phase shift of antenna array element of spherical wave is established based on the 3D precise geometric relationship of the single-bounce concentric-cylinders scattering. Second, a birth-and-death model for the non-stationary characteristics in the massive MIMO array direction is developed. The channel statistical characteristic function of the proposed model is derived, and the theoretical deduction is verified by comparing the results of the characteristic function theory value and Monte Carlo statistics value. In addition, the differences of spatial correlation between the proposed model and the traditional ground-air 3D MIMO channel model based on plane wave are analyzed and compared by simulation. The simulation results show that the two models have almost no difference under the near field. And there are differences between the two models under the far field, the traditional model is no longer applicable. Finally, the simulation results of several channel characterizations and the actual test data of open literatures for ground-air channel are compared and analyzed. The results show that, as a general applicability model, the parameters of proposed model can be optimized according to the test conditions, test environment and test results of the channel in order to approach the actual channel to accurately model the specific channel.

channel model; Massive MIMO; channel statistics character function; non-stationary characteristic; concentric-cylinders scattering; far field model

2016-05-31； Revised：2016-10-17； Accepted：2016-11-04； Published online：2016-11-10 14:18

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0288

2016-05-31； 退修日期：2016-10-17； 录用日期：2016-11-04； 网络出版时间：2016-11-10 14:18

www.cnki.net/kcms/detail/11.1929.V.20161110.1418.005.html

＊通讯作者.E-mail: sportxin_558@163.com

王鑫， 张晓林， 曹晏波． 一种地空3D-Massive MIMO信道模型[J]． 航空学报, 2017, 38(3): 320484. WANG X, ZHANG X L, CAO Y B. A 3D-Massive MIMO ground-air channel model[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(3): 320484.

V243.1; TN911

A

1000-6893(2017)03-320484-16