反演设计的三维空间微重力模拟系统控制系统
2017-11-17林森海姚春红张文辉陈荣昌朱银法
江 洁,林森海,姚春红,张文辉,陈荣昌,朱银法
(1.丽水学院 工学院,浙江 丽水 323000; 2.浙江斯凯瑞机器人股份有限公司,浙江 丽水 323000; 3.庆元县农业局,浙江 丽水 323000)
浙江省教育厅基金资助项目(Y201534043);浙江省科技厅基金资助项目(2015C31160);丽水市高层次人才资助基金资助项目(2015RC04);丽水市科技计划基金资助项目(2015KCPT03)
江 洁(1981—),女,实验师.E-mail:jj2196@163.com
反演设计的三维空间微重力模拟系统控制系统
江 洁1,林森海2,姚春红3,张文辉1,陈荣昌2,朱银法1
(1.丽水学院 工学院,浙江 丽水 323000; 2.浙江斯凯瑞机器人股份有限公司,浙江 丽水 323000; 3.庆元县农业局,浙江 丽水 323000)
针对目前做复杂运动的大中型飞行器地面微重力环境难以实现的问题,设计了新颖的模拟装置,并提出了基于反演的自适应补偿控制方法.该装置采用剪式升降系统、轴承导向系统、电机驱动系统、气悬浮系统等组合的方式来实现复杂运动的三维微重力模拟.该系统采用气悬浮方法来实现二维平面随动,采用力反馈的主动控制方法来补偿重力,实现竖直方向升降.在考虑系统精确模型难以获得及存在外界干扰的情况下,提出了基于后推的自适应控制方法保证了系统的鲁棒性,设计了自适应控制律,实现了对系统不确定模型的实时估计.试验表明,在目标重力突变的情况下,控制系统依然能达到较高模拟精度,对于复杂空间运动的飞行器微重力模拟具有重要工程价值.
三维微重力; 地面模拟系统; 反演设计; 自适应控制
空间飞行器发射升空后一旦出现问题就难以维修,面临废弃.我国于2006年发射的“鑫诺二号”卫星就是个惨痛的例子,该卫星的太阳帆板及通讯天线未按要求展开,从而变成一颗废星.忽略科研人员的巨大人力成本,单颗卫星造价就耗资20亿人民币.因此,飞行器在升空前进行充分的地面高精度模拟实验来验证性能指标是非常必要的.
然而,当前国际上空间微重力地面模拟技术与其对应的空间其他技术相比却相对滞后,这正成为阻碍空间技术发展的瓶颈,因此,对其进行深入探索和研究具有重要意义.
空间微重力模拟作为空间技术的一个重要衍生领域,经过半个世纪的发展,相续出现了4种模拟方法,即落塔法、悬吊法、水浮法和气浮法等[1-2].落塔法是在微重力塔中或高空飞机中对目标实行自由落体运动,进而产生短暂微重力的一种方法.该方法可以进行复杂三维空间微重力试验,但造价昂贵,实验时间过短,难以对性能进行充分考核.悬吊法是通过吊丝悬挂目标物来平衡飞行器自身重力[5-6].该方法可以进行三维模拟,但吊丝易晃动,吊轮路径的导轨轨迹布局复杂,摩擦阻力大,只能适用于轻型飞行器.水浮法是利用水的浮力来平衡目标重力的方法[7-8].该方法可以进行三维空间微重力模拟,但水浮方案容易受水阻力和紊流影响,模拟精度较差,同时要求试验期间密封性好,试验环境苛刻.气浮法是利用气浮轴承将飞行器托在平整光滑的平台上,通过喷气悬浮力抵消飞行器重力是目前空间微重力环境模拟试验最广泛的方法[9-12].但气浮法仅限于在水平面上进行二维仿真试验,由于飞行器姿态运动比较复杂,运动部件在很多情况下,不仅要完成水平展开,在竖直方向及多自由度旋转方向均要完成相应的展开动作,因此,单纯气浮法无法满足要求.针对此类问题,文献[10]提出了采用气浮与气缸结合的方式来实现三维微重力模拟.但气源压力不稳定性、气缸自重及粘滞阻力等会影响到系统响应速度,且其采用的神经网络算法需要大量学习样本,应用对象仅限于微型飞行器,这些缺点均影响了工程应用价值.
综上所述,现有微重力模拟方法难以满足地面实验需要,针对此类情况,本文设计了新颖的三维空间微重力地面模拟装置,并提出了基于反演的自适应补偿控制方法.该装置采用剪式升降系统、轴承导向系统、电动机驱动系统、气悬浮系统等组合的方式来实现复杂运动的三维微重力模拟.该系统采用气悬浮方法来实现二维平面随动,采用力反馈的主动控制方法来补偿重力,实现竖直方向升降.在考虑系统精确模型难以获得及存在外界干扰的情况下,提出了基于后推的自适应控制方法,保证了系统的鲁棒性,设计了自适应控制律,实现了对系统不确定模型的实时估计.试验表明,在目标质量突变的情况下,控制系统依然能达到较高模拟精度,对于复杂空间运动的飞行器微重力模拟具有重要工程价值.
1 三维空间微重力环境地面模拟系统
1.1三维空间微重力模拟地面装置结构
任意复杂三维空间运动都可以分解为二维水平平动和一维竖直运动.设计三维微重力模拟装置结构如图1所示.该实验方案充分考虑了工程实际中实验场所的空间限制以及大中型飞行器在展开过程中的空间要求,设计了剪式升降机构来最大限度节约空间.

图1 三维空间地面模拟试验设备结构图Fig.1Three-dimensional ground simulationtest equipment structure diagram
所设计的三维空间微重力地面模拟装置的主要工作原理:气足为整个直推式三维升降气足提供水平零重力模拟环境;伺服电动机接收控制器的控制信号并带动丝杠进行旋转,进而实现剪式升降支架的竖直升降;导向伸缩杆辅助实现升降支撑,压力敏感器用于测量目标飞行器的重力信息,实现力反馈.该装置的优点不仅在于充分利用了机电传动技术,而且巧妙设计的剪式升降机构,使得装置结构更加紧凑,且具有了较大的伸缩比,大幅增加了运动距离,更易满足试验目标的运动行程要求,降低了对实验空间的要求.
1.2系统动力学模型的建立
将机电传动系统、压力传感器、试验对象均看为质量、阻尼、刚度模型,则三维空间微重力地面模拟装置与环境的接触可以粗略用图2表示[13-14].
图2给出了传动装置/压力传感器/接触环境在一个方向上的模型.{Kd,Cd},{Ks,Cs}及{Kr,Cr}分别为各自接触刚度和阻尼系数,Fc和Fs分别为控制输出和传感器输出.

图2 传动系统力学模型Fig.2 Mechanical model of transmission system
据图2可建立其输入/输出关系:
X2/Fc=B2/A
X3/Fc=B3/A
(1)
式中:B3=(crs+kr)(css+ks);B2=[mrs2+(cs+cr)s+ks+kr](cds+kd);A=[mds2+cds+kd][mds+(cd+cs)s+(kd+ks)][mrs2+(cd+cr)s+(ks+kr)]-[mrs2+(cr+cs)s+ks+kr].其中s为拉普拉斯算子.
由刚度控制得传感器的测量力Fs输出:
Fs=ks(X2-X3)
(2)
将式(1)代入式(2)得

(3)
2 基于反演设计的自适应控制
由于力传感器刚度远小于环境刚度,忽略传感器动力学参数,则系统被控模型为

(5)
式中:cb=cd+cr为综合阻尼系数.

将式(5)转化为状态方程为

(6)

考虑到在工程实际中的测量水平及人为因素等原因,精确的数学模型难以建立,特别是质量、刚度及阻尼系数均无法准确测得,因此只能获得对其的估计值,并考虑到摩擦及干扰的不确定性,这里定义为d,则被控对象数学模型实际应为
(7)

将式(7)可进一步整理为
(8)
式中:f=ΔK1x1+ΔK2x2+ΔK3u+d为总的不确定部分.设x1d为期望的输出力指令,e为力误差,则
e=x1-x1d
(9)
则
(10)
设k为误差系数常数,则虚拟项为
ε=ke
(11)
后推1
定义如下Lyapunov函数:

(12)
设

(13)
将式(10)代入式(13)可得
(14)
则将式(12)两边微分,并联立式(11)及(14)可得
e(E-ε)=
eE-ke2
(15)
后推2
设ρ为切换函数,λ>0,且
ρ=λe+E
定义Lyapunov函数为

(16)
将式(16)两边微分可得
(17)
将式(14)两边微分可得
(18)
将式(18)代入式(17)可得
(19)
后推3


(20)
定义Lyapunov函数为
(21)
为了对系统不确定部分f进行估计,由式(21)可推得自适应控制律为

(22)
则基于后推的自适应器设计为
α[ρ+βsgn(ρ)]}
(23)
式中:α及β为正的常数.
将式(22)及式(23)代入式(21)得
(24)
取
设定合适的α,k及λ的值,则Q>0,即Q正定.
令
则
(25)
故式(24)可写为
(26)
3 试验验证
由于任意复杂的空间运动都可以分解为一个三维运动,即水平运动和竖直运动.由于水平方向依靠气足随动,因此,主要验证在竖直分量力的作用下,升降装置对试验目标质量的补偿情况.
整个运动过程持续10 s,本文进行如下3种典型运动状态设定:①t=0 s静止,试验目标质量为51 kg,目标从初始静止状态开始运动,在竖直方向上运动了3 s;② 在t=3 s时,试验目标抓取一质量为102 kg负荷(忽略抓取过程),总质量变为153 kg,继续运动;③ 在t=6 s时,试验目标释放一质量为71.5 kg的负荷,总质量变为81.5 kg.
仿真结果如下:图3为试验目标重力补偿图,图4为重力补偿误差曲线图,图5为对于自适应控制器对系统不确定部分估计,图6为控制器力矩.

图3 目标重力的补偿曲线Fig.3 The compensation curve of target gravity

图4 重力补偿误差曲线图Fig.4 Gravity compensation error curves

图5 不确定部分估计值Fig.5 Estimated value of uncertain parts
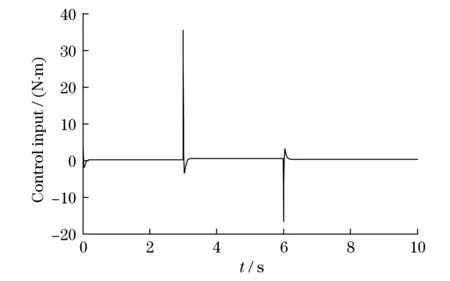
图6 控制力矩Fig.6 Control torque
由图3~图4中可以看到,所设计的系统能够对目标质量进行很好的补偿,大约在到0.5 s的时间内就能从0 N迅速达到500 N,即补偿了51 kg,从而实现对目标重力完全补偿.在t=3 s,目标抓取质量为102 kg的负荷后,整个目标质量达到153 kg,模拟系统能够在大约1 s内(t=4 s时)达到较好补偿,在2 s内(t=5 s时)就能达到1 500 N,即实现了补偿153 kg的完全补偿;在t=6 s 时,此时目标释放一质量为71.5 kg的负荷,总质量变为81.5 kg,由图中可以看出,模拟系统能够在不到1 s内达到预期800 N,即81.5 kg的补偿效果.图5可以看出自适应控制器在两次模型突变过程中,均能够较好及时估计系统不确定模型.图6中为控制力矩输出图,两次抓取和释放造成控制力矩出现较大突变,但是控制器能够及时响应,并输出所需控制力矩,说明该控制器具有较好的动态特性和控制精度.
针对所设计的微重力模拟系统控制实验结果表明,所采用反演自适应控制器能够达到了较好微重力环境模拟效果.
4 结论
针对做三维空间运动的飞行器,其微重力环境难以模拟这一难点问题,设计了剪式升降的三维微重力地面模拟系统,并提出了基于后推的自适应控制方法,获得了如下结论:
(1) 提出了一种由剪式升降系统、轴承导向系统、电动机驱动系统和气悬浮系统的组合装置,具有附加质量轻、结构紧凑、运动空间大、易于实现的优点.
(2) 提出了后推的自适应控制方法,保证了系统鲁棒性;设计了自适应控制器,实现了对系统不确定模型的实时估计.
(3) 试验验证了在目标重力突变的情况下,所设计的空间微重力模型系统的有效性,具有重要工程价值.
[1] 徐文福,梁斌,李成,等.空间机器人微重力模拟实验系统研究综述[J].机器人,2009,31(1):88-96.
XU W F,LIANG B,LI C,et al.A review on simulated micro-gravity experiment systems of space robot[J].Robot,2009,31(1):88-96.
[2] 史士财,吴剑威,崔平远,等.空间机械臂全局反作用优化及地面试验研究[J].机器人,2009,31(3):242-248.
SHI S C,WU J W,CUI P Y,et al.Global reaction optimization of space manipulator and its ground test[J].Robot,2009,31(3):242-248.
[3] SAWADA H,UI K,MORI M,et al.Micro-gravity experiment of a space robotic arm using parabolic flight[J].Advanced Robotics,2004,18(3):247-267.
[4] 高德鹏,杜庆安,吴锐.月球六分之一微重力环境模拟装置的设计与实现[J].计算机测量与控制,2016,24(2):137-142.
GAO D P,DU Q A,WU R.Design and implementation of one-sixth microgravity environment simulator on moon[J].Computer Measurement & Control,2016,24(2):137-142.
[5] GREGORY C W,XU Y.An active vertical-direction gravity compensation system[J].IEEE Transactions on Instrumentation and Measurement,1994,43(6):769-792.
[6] 张文辉,叶晓平,季晓明.空间微重力地面模拟装置基于神经滑模的自适应补偿控制[J].机械工程学报,2014,50(15):68-72.
ZHANG W H,YE X P,JI X M.Adaptive compensation control for ground simulation equipment of space microgravity environment base on neural sliding-model[J].Chinese Journal of Mechanical Engineering,2014,50(15):68-72.
[7] GEFKE G G,CARIGNAN C R,ROBERTS B J,et al.Ranger telerobotic shuttle experiment:status report[C]// Telemanipulator and Telepresence Technologies VIII Matthew R.Stein Boston:MA.2001:123-132.
[8] 姚燕生,梅涛.空间操作的地面模拟方法-水浮法[J].机械工程学报,2008,44(3):182-188.
YAO Y S,MEI T.Simulation method of space operation on the ground-buoyancy method[J].Chinese Journal of Mechanical Engineering,2008,44(3):182-188.
[9] 金飞虎,洪炳熔,柳长安.双臂自由飞行空间机器人捕捉目标实验研究[J].宇航学报,2002,23(l):64-68.
JIN F H,HONG B R,LIU C A.Experiment research of a dual-arm free-flying space robot capturing a target[J].Journal of Astronautics,2002,23(l):64-68.
[10] 陈三风,梅涛,张涛,等.空间微重力环境地面模拟系统的控制器设计[J].机器人,2008,37(3):201-204.
CHEN S F,MEI T,ZHANG T,et al.Design of the controller for a ground simulation system of spatial microgravity environment[J].Robot,2008,37(3):201-204.
[11] SONG J Y,YAO D Y,HU J M,et al.A novel calibration system for a space manipulator[C]// Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway,NJ,USA:IEEE,2006:4672-4677.
[12] 訚耀保,荒木献次.具有非对称气动伺服阀的气动压力控制系统建模与分析[J].中国机械工程,2009,20(17):2108-2111.
YAN Y B,HUANG M X C.Analyses on the mathematical models of valve controlled unsymmetrical cylinder in an active servo loading system[J].Chinese Mechanical Engineering,2009,20(17):2108-2111.
[13] 邱志成,谈大龙.基于加速度反馈的柔性关节机械臂接触力控制[J].机械工程学报,2002,38(10):37-41.
QIU Z C,TAN D L.On acceleration sensor-based feedback control for contact force of the flexible joint manipulator[J].Chinese Journal of Mechanical Engineering,2002,38(10):37-41.
[14] LIN F J,SHEN P H,HSU S P.Adaptive backstepping sliding mode control for linear introduction motor drive[J].IEE Proceeding Electrical Power Application,2002,149(3):184-194.
Adaptivecontrolsystemstudyofgroundsimulationsystemforthree-dimensionspatialmicrogravitybaseonbackstepping
JIANGJie1,LINSenhai2,YAOChunhong3,ZHANGWenhui1,CHENRongchang2,ZHUYinfa1
(1.School of Engineering,Lishui University,Lishui 323000,Zhejiang, China; 2.Zhejiang Skerry Robot Co.,Ltd.,Lishui 323000,Zhejiang, China; 3.Qingyuan Agricultural Bureau,Lishui 323000,Zhejiang, China)
Difficult problems of simulation the space microgravity environment for big and middle experimental objects with complex move are considered.A novel microgravity ground simulation system is presented by the paper.The equipment combine scissors lifting,bearing guide,motor drive and air-bearing to realize to realize 3-D motion function.Dynamics model is developed by this paper.Considering the system modeling error,adaptive controller is designed to identify and compensate unknown uncertainty of system.Complicated system is decomposed into several simple subsystems,and then control law is designed.Controller based on the backstepping theory ensures control system stability and robustness.Experiment results show that three dimensional microgravity simulation systems can achieve good accuracy and has high value for engineering application.
three-dimensional microgravity; ground simulation system; backstepping design; adaptive control
TP 273
A
1672-5581(2017)04-0305-05
