机器人制孔自适应蚁群路径规划算法*

刘艳梅，王 鑫，马跃晏

（沈阳航空航天大学自动化学院，沈阳 110136）

机器人制孔自适应蚁群路径规划算法*

刘艳梅，王 鑫，马跃晏

（沈阳航空航天大学自动化学院，沈阳 110136）

随着现代飞机制造制孔技术的不断发展，对制孔效率、定位精度及加工质量提出更高的要求。采用CATIA软件建立飞机部件模型，提出自适应蚁群算法并应用于机器人制孔路径规划设计中。仿真实验表明，信息素挥发因子的大小对算法的全局搜索能力及收敛速度有直接影响，提出的自适应蚁群算法通过动态调整信息素挥发因子，充分改善了制孔方式的无目的性、生成的路径质量低等一些不足之处，从而实现机器人制孔路径规划的最优。

CATIA，自适应蚁群算法，机器人制孔，路径规划

0 引言

在飞机装配制孔方面，传统的人工制孔方法已经不能满足现代飞机制造业的需求。随着机器人技术的不断发展，机器人自动制孔已被应用于飞机制造业，除了能够满足飞机生产的数量大、时间紧的要求，还提升了飞机装配过程中制孔的定位精度以及质量，延长了飞机零部件的使用寿命。在国际上，机器人自动制孔系统已经十分成熟，并被广泛应用于军用飞机、民航飞机的实际生产中。在我国，对机器人自动制孔技术的研究相对落后，在飞机装配制造中的应用开发也存在不足。20世纪90年代以来，国内开始陆续引进自动制孔设备，但并未形成生产力，飞机装配仍然以手工装配为主。而国外自动制孔技术和设备的研制与应用已经达到了较高的水平。在机器人制孔的研究领域里，路径规划算法［1］是目前研究领域中最重要的部分。路径规划的一般性问题是按照一定的评价标准，机器人制孔从起点运动到终点，能够安全，高效地完成制孔任务。路径规划算法的种类繁多，目前，国内外提出了很多算法，如蚁群算法、遗传算法［2］和粒子群算法等解决机器人制孔路径规划问题。20世纪90年代意大利学者Dorigo和V.Maniezzo最早提出了蚁群算法［3］，是一种源自于自然界的蚁群觅食行为的活动规律启发提出的模拟进化算法。蚁群算法作为新式的优化算法，它的正反馈性、协同性和隐含的并行性使其具备不错的发展潜力，灵活性让它在解决组合优化问题上拥有杰出的适应性。但是传统的蚁群算法存在许多不足之处，需要进一步改进，因此，针对传统蚁群算法的改进是目前研究方向热点之一。

本文基于CATIA软件建立飞机零部件模型［4］，并提取所需要的制孔点位置，通过蚁群算法对设计出的零部件进行路径规划。由于蚁群算法容易出现收敛速度慢和搜索全局最优值能力低，所以提出一种自适应的动态调整该算法中的信息素挥发因子策略，然后通过不断地迭代，蚂蚁以更大的概率选择一条最短路径来实现机器人自动制孔。

1 飞机部件模型的建立

CATIA软件的功能是飞机产品建模软件中最强大的一款，能够实现整个飞机制造的工业设计流程，提供全流程开发的工作环境。通过建立数字化的开发环境，给使用者提供了一个面向整个设计制造过程，并对每个部分进行模拟仿真，并通过电子通信实现工程人员和非工程人员的信息交流，及时处理出现的问题。本文基于某飞机部件，在CATIA中创建工艺数模，针对不同的孔类型进行设计，得到所有的制孔类型，并拾取所有机器人制孔的孔位点，如图1所示。

图1 飞机零部件模型

基于CATIA软件建立上述飞机零部件模型，然后提取所需要的制孔点的点位坐标。机器人制孔的制孔过程实际上就是路径规划问题。而路径规划的优劣直接影响其智能化程度的水平，所以选择一种最优的路径规划算法对于机器人制孔来说，至关重要。

2 蚁群算法基本原理

蚁群算法是一种基于群体智能寻优的启发式搜索算法［5］。该算法根据蚂蚁觅食的原理，任意两点表示蚂蚁的起点和终点，初始阶段群体根据相同概率均匀地选择每条路径，蚂蚁在寻找食物所经过的路径上释放一种挥发性分泌物（称信息素，该物质随时间的推移逐渐挥发消失，信息素浓度的大小表示路径的远近）。其信息素量决定前行方向，并且蚂蚁在寻找食物的过程中会感知信息素强度。蚂蚁选择下一个节点是通过转移概率，依次类推，最终选择移动到终点。每条路径上通过蚂蚁的数量由信息素浓度决定，浓度越高蚂蚁选择该路径的可能性就越大。蚂蚁选择当前路径的概率会随着信息素的挥发和遗留相应发生变化。不断地更新信息素导致多个路径上的蚂蚁都逐步凑集到最短路径上，即找到一条可行的最短路径。通过简单的模型分析蚁群如何通过信息交流与传递的协作寻找食物，最终获得蚁穴与食物之间最短路径的过程。如图2所示。

图2 模拟蚂蚁觅食原理图

设蚂蚁从A点出发，食物在E点。BH、HD距离为1，BC、CD距离为0.5。假设30只蚂蚁由A到E，30只蚂蚁由E到A，蚂蚁速度设为1。在t=0时刻，每一条路径的信息素都为0。第1批从A出发的蚂蚁选择路径BHD和BCD概率相同，且蚂蚁数各为15。同理，从E出发的蚂蚁，假设选择路径DHB和DCB的蚂蚁数各为15。在t=1时刻，第2批从A出发的蚂蚁会发现在路径BH的信息素强度为15。由第1批从B经C向D的15只蚂蚁和从D经C向B的15只蚂蚁共同留在路径AB的信息素强度为30。由于路径BC的信息素强度高，则第2批30只蚂蚁选择BC这条路径的概率要高于选择BH的概率。同理，第2批从E出发的30只蚂蚁也会有20只蚂蚁选择路径DCB，有10只蚂蚁选择路径DHB。通过不断地循环，BCD路径上聚集的信息素强度越来越大，最终所有蚂蚁都选择走这条路径。如图2可以看出，蚂蚁组成的蚁群的集体行为便表现出一种信息正反馈现象。通过这种正反馈机制，蚂蚁最终可以发现最佳路径，且绝大多数的蚂蚁都会沿着同一条路径到达食物源。

3 基于自适应蚁群算法的机器人制孔路径规划

典型的路径规划是指，在具有障碍物的工作环境下，按照一定的评价标准，寻找一条从起始状态到目标状态的无碰撞路径。路径规划的优劣直接影响机器人制孔［6］的定位精确、效率程度，所以机器人制孔要选择一种优秀的路径规划算法。目前已存在许多优化算法用来解决该问题，但某些算法存在一定的局限性。本文在充分分析各种算法优缺点基础上，用自适应蚁群算法进行设计路径规划，从而找到一条最优路径实现机器人制孔来完成飞机零部件。

蚁群算法主要依据信息正反馈原理和某种启发式算法的有机结合。正反馈原理是强调解的性能，但易出现堵塞和停滞现象。蚁群算法出现不足之处的根本原因是解决问题时易出现早熟和局部收敛现象。为解决这一问题，在王颖等的论文［7］中，说明了自适性蚁群算法的基本思想。在蚁群算法的基础上，引入自适应调整策略，在求解的过程中，解决蚁群算法的局部和全局搜索能力及其收敛速度。而针对路径规划问题，蚁群算法中挥发因子的大小直接关系到蚁群算法在求解问题时的全局搜索能力，或者局部搜索能力以及收敛速度。为了解决传统蚁群算法出现的问题，在参考文献［8］中提出了各种不同的更新信息素挥发因子的策略。考虑到算法的全局搜索能力和收敛速度等问题，提出了自适应的对蚁群算法中挥发因子ρ的值进行改变，可以对传统蚁群算法的不足进行改进，此算法属于自适应算法。

自适应蚁群算法路径规划具体实现过程如下：

3.1 自适应蚁群算法初始化

在算法的初始时，假设在各个路径上的信息素浓度都是相等的。设蚂蚁的数目为m只，分别放在n个孔位点上；令初始时刻t=0；循环次数计数器NC=0，则最大代数为NCmax；信息素强度初值

在每次循环过程中，将m只蚂蚁分散到n个制孔点的位置，这一条件通过列表tabek来实现，并记录每一轮模拟蚂蚁k已经走过的各个制孔点，其中k=（1，2，3，…，m）。该列表存储了 t时刻前每只蚂蚁在本次循环过程中访问过的所有制孔点位置，借此可以限制在本次循环过程中再次访问已经访问过的制孔点。同时，由于列表涵盖了每只蚂蚁经过制孔点的顺序，计算每只蚂蚁在本次循环中走过的总路径长度，并得到蚁群算法优化的当前解。

3.2 选择下一个制孔点

蚂蚁k的转移概率决定制孔点i是否访问下一个制孔点j。定义在t=0时刻，某一只蚂蚁k由点i移动到点j的概率Pijk与能见度和信息素有关，其表达式为：

式中，ηij为计算各个孔位点之间的距离（i，j）上的先验知识或称为能见度，其值与时间无关，而与孔位点间的距离有关，即ηij=1/dij，dij是点i和j之间的距离；α为启发式因子，表示路径上残留信息素的相对重要性，其值反应了随机性因素在路径搜索中的作用；β为期望启发式因子，表示路径的能见度的重要性，其值反应蚁群在路径搜索中确定性因素的作用；Jk（i）为蚂蚁k在制孔点i之前没有访问过的制孔点位置的集合，与列表相关联；allowedk表示下一步访问的制孔点，列表tabek中已经访问到的除外。

3.3 自适应蚁群算法挥发因子调节策略

在蚁群算法中，衡量信息素挥发速度的参数是信息素挥发因子，因而ρ的大小对算法的执行时间、全局搜索能力及收敛速度有直接的影响。传统蚁群算法在搜素过程中进行多次迭代，而且每次迭代都需要多只蚂蚁一起搜索，这样降低了该算法的收敛速度。该算法在处理规模庞大时，由于信息素不断挥发，逐渐减少到0，从而不再被搜索，这样会导致一些路径很少或从来没被访问到，因此，大大地降低了该算法的全局搜索能力。一般情况下ρ的初始值的取值范围在0.1～0.9之间，初始值不同所得到的路径长度就有所不同。所以对初始值从0.1～0.9进行实验，得到相对应的路径长度，如图3所示。

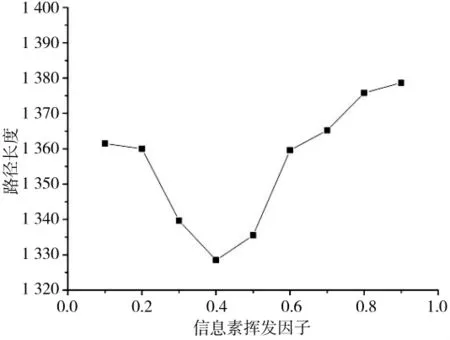
图3 挥发因子ρ与路径长度的关系图

由图3可以看出，ρ值在0.1～0.6范围内得到曲线较理想，在0.7～0.9的曲线不理想，而在0.4与0.5时得到的路径长度最为理想。由此可知，通过改变挥发因子ρ值的大小来达到想要的最优路径效果。即设置初始值ρ=0.4，这样可以避免局部搜索情况的出现。当全局搜索经过多次还是没有达到想要的结果，并出现传统蚁群算法的收敛速度慢和全局最优解的搜素能力低等问题，提出了一种自适应蚁群算法。即对信息素挥发因子ρ进行适当的改变。其表达式为：

这样可以防止ρ过大，路径上信息素挥发速度快，蚂蚁之间的相互影响变小，算法收敛的收敛速度变慢，甚至使算法最终解的优化程度降低；ρ过小，路径上的信息素保留时间长，有可能再次搜索到已有路径，从而对算法的随机性能和全局搜索能力产生不利影响。

3.4 更新信息素

信息素作为蚂蚁进行群体信息交流的重要手段，也是实现路径选择的重要依据。每只蚂蚁在t时刻依据转移概率选择下一制孔点，并在t+1时刻到达终点。经过n个时刻，路径（i，j）上的信息素将进行更新，其表达式为：

式中 ρ∈（0，1），称信息素挥发因子，即表示每个连接上的信息素浓度自动减弱的过程，而1-ρ代表依次循环中信息素的挥发程度是孔位点i和点j之间的路径（i，j）在 t时刻的信息素强度为所有蚂蚁在路径（i，j）上单位长度的信息素量为第 k 只蚂蚁在（t，t+n）时间段留在路径（i，j）上单位长度的信息素量。M.Dorigo提出了3种不同的蚂蚁算法模型，依据不同的信息激素更新的策略分别是蚂蚁圈模型、蚂蚁数量模型及蚂蚁密度模型，其差别是运用不同的求法求解根据全局整体的路径优化，使蚂蚁完成一次迭代后更新所有路径上的信息素。其采用蚂蚁圈模型表达式为：

式中，Q为信息素强度；Lk为第k只蚂蚁完成一次循环走过路径的长度。从式（2）和式（3）中可以看出，对于某一条路径（i，j）的信息素强度取决于上一次循环完成后的信息素强度和本次循环过程中信息素的积累在本次循环过程中，如果经过这条路径的蚂蚁数量多，则留下的信息素量就相对大；经过这条路径的蚂蚁在本次循环过程中走过的总路径越短，则对这条路径信息素强度的贡献就越大。

3.5 满足迭代终止条件，输出结果。否则NC=NC+1，转3.2，进行下一代进化

自适应蚁群算法提高了传统算法的性能。随着时间的渐渐进行，传统的蚁群算法在全局搜素过程中，蚂蚁存留下来的信息素会慢慢消失在搜素的范围内，使得该算法的全局搜素能力降低。自适应蚁群算法通过改变信息素挥发因子策略，增强了该算法的全局搜素能力和全局收敛速度，实现了一条最短路径。

4 机器人制孔路径规划仿真结果

为了验证自适应蚁群算法的有效性，本文设计并实现了机器人制孔路径规划仿真实验。实验中选取的参数为：蚂蚁群体的个数m=100，启发式因子α=2，自启发式因子β=3，常数 Q=1，迭代次数NC=500。本文采用自适应蚁群算法设计路径规划，并在MATLAB软件的平台下进行仿真。仿真结果表明，改进后的蚁群算法比传统蚁群算法具有更好的搜索最优解的能力。如图4是大多数蚂蚁选择前往目标点的一条路径，是该工作环境模型下所能找到的最优路径，即完成机器人制孔的一条最短路径。

图4 自适应蚁群算法优化路径

对上述算法中ρ进行测试，ρ值的大小直接影响算法的收敛性和搜素能力。本文自适应蚁群算法在最优解、路径长度上都有所改善。为了更加直接地展现自适应蚁群算法在搜索过程中具有一定的方向性，可通过仿真，得到自适应蚁群算法和基本蚁群算法的收敛性曲线图，如下页图5、图6所示。

图5 蚁群算法收敛图

图6 自适应蚁群算法收敛图

通过仿真结果对传统算法和自适应算法的收敛曲线进行对比分析，容易看出，传统蚁群算法的机器人路径规划最短路径长度为1 360.796 0，而自适应蚁群算法的机器人路径规划的最短路径长度为1 328.512 1。自适应蚁群算法比传统蚁群算法更精确、更稳定。从计算时间和规划路径来看，自适应蚁群算法规划机器人路径收敛速度更快，使用的时间更少，全程路径长度更短，明显优于传统蚁群规划方法，并解决了全局搜索能力和收敛速度慢的问题。

5 结论

本文通过CATIA软件对飞机零部件进行三维建模。针对机器人制孔路径规划问题，提出了自适应蚁群算法，即适当地对搜索过程中信息素因子ρ进行改变，使传统蚁群算法更容易搜索目标，并提高该算法的收敛速度和搜索全局最优值的能力。从时间和空间来看，提高了收敛性和搜索能力等特性，表明自适应蚁群算法克服传统蚁群算法的缺点，为机器人制孔路径规划提供了指导。经仿真结果可以看出，通过提出的自适应蚁群算法，对设计出的零部件得到了一条最优路径来实现机器人制孔，并取得较好的效果。

［1］于雷，任波，鲁艺.自适应蚁群算法的多机协同空战目标分配方法［J］.火力与指挥控制，2008，33（6）：49-51.

［2］杨敬辉，洪炳镕，朴松昊.基于遗传模糊算法的机器人局部避障规划［J］.哈尔滨工业大学学报，2004，36（7）：946-948.

［3］TAN G Z，HE H，SLOMAN A.Ant colony system algorithm for real-time globally optimal path planning of mobile robots［J］.Automatica Sinica，2007，33（3）：279-285.

［4］韩志仁，郭文杰.基于MBD飞机装配自动制孔路径规划研究［J］.机械设计与制造，2015，10（10）：201-203.

［5］吴小文，李擎.果蝇算法和5种群智能算法的寻优性能研究［J］.火力与指挥控制，2013，38（4）：17-20.

［6］彭喜元，彭宇.群智能理论及应用［J］.电子学报，2003，31（12）：35-37.

［7］王颖，谢剑英.一种自适应蚁群算法及其仿真研究［J］.系统仿真学报，2002，14（1）：31-33.

［8］LI Y J，WU T J.Anadaptiveant colonysystem algorithm for continuous-space optimization problems ［J］.Journal of Zhejiang University Science，2003，4（1）：40-46.

Research on Adaptive Ant Colony Algorithm in Robot Hole Making Path Planning

LIU Yan-mei，WANG Xin，MA Yue-yan
（School of Automation，Shenyang Aerospace University，Shenyang 110136，China）

With the development of aircraft manufacturing industry robot technology，in the process of modern aircraft manufacturing hole making technology has become more high efficiency，more accurate positioning and more high processing quality，in this paper，the CATIA software is used to build the aircraft component model，adaptive ant colony algorithm is proposed and applied to the design of robot path planning to get the shortest path between the origin and destination point.Simulation experiment result shows that the size of pheromone volatile factor has a direct influence on the global search ability and convergence speed of the algorithm.So adaptive ant colony algorithm adjusts the dynamic of pheromone volatile factor to improve the non-purpose of the way of making holes，the low path quality，and realizes the optimal path planning of robot hole making.

CATIA，adaptive ant colony algorithm，robot hole making，path planning

1002-0640（2017）10-0142-05

V262.4

A

10.3969/j.issn.1002-0640.2017.10.030

2016-09-15

2016-10-22

航空科学基金资助项目（2015ZE54026）

刘艳梅（1974- ），女，吉林松原人，博士，副教授。研究方向：系统建模与控制。