倾斜发射装置发射过程弹箱姿态仿真分析

王玎楠，王学智

（空军工程大学防空反导学院，西安 710051）

倾斜发射装置发射过程弹箱姿态仿真分析

王玎楠，王学智

（空军工程大学防空反导学院，西安 710051）

为研究倾斜发射装置的导弹与发射箱在发射过程中的姿态变化，通过改进的Craig-Bampton方法将转台、起落架、发射箱、车架等构件进行柔性处理，并与发射装置多刚体动力学模型结合，建立了倾斜发射装置刚柔耦合模型，并对模型进行了频率验证。之后针对3种发射条件下弹箱俯仰角的变化情况进行了仿真分析，得出了发射角度选取的相关结论。

倾斜发射，发射过程，弹箱姿态

0 引言

导弹的发射精度是衡量导弹性能的重要指标，初始扰动是影响导弹发射精度的主要因素之一［1］。地空导弹发射装置经常采用的发射方式之一即是倾斜发射方式，对于采用倾斜发射方式的发射装置而言，在发射过程中弹箱之间的相对运动所引起的动力学响应会对导弹的初始扰动产生关键性影响。在导弹发射过程中，发射装置的振动情况将会直接影响导弹的发射精度，而振动大小则可以通过弹箱姿态等动力学响应体现出来。

倾斜发射装置属于复杂机械系统，其由大量部件构成。在发射过程中，外力作用对于发射装置的转台、起落架、发射箱、车架等构件将产生难以避免的影响，从而进一步影响到导弹的动力学响应，在建模时需将这些构件作为柔性体处理［2］。对于此类复杂多体系统，使用传统的有限元离散化方法对柔性体进行处理会使得整个系统的自由度达到相当高的数量，从而极大地增加了计算量。动态子结构模态综合法则为解决此类复杂多体系统的模态计算问题提供了便利，运用该方法可较大幅度地减少整个系统的自由度而不会改变系统本身的运动特性。

关于运用模态综合法进行柔性体模化处理，许多学者都进行了不同程度、不同对象的研究。2009年，张涛等通过使用C-B模态综合法，将ADAMS与ANSYS结合使用，建立了导弹发射系统刚柔耦合模型，对导弹的发射姿态等动力学响应进行了仿真分析［3］；2015 年，高星斗等［2］将改进的 C-B 模态综合法与多体动力学理论相结合，建立了发射装置刚柔耦合模型，并针对不同部件对发射箱下沉量的影响进行了对比分析，得到了下沉量影响因子。

本文将倾斜发射装置作为研究对象，通过改进的Craig-Bampton方法［4-5］将发射过程中变形较为明显的构件如转台、起落架、发射箱、车架等进行柔性处理，并将处理后的柔性体模型与倾斜发射装置多体动力学模型相结合，建立了发射装置刚柔耦合模型，对发射过程中导弹、发射箱的俯仰姿态的变化进行不同工况下的仿真分析，得到了导弹姿态及发射箱振动响应与高低角选取之间的对应关系，同时验证了模型建立方法的正确性。

1 Craig-Bampton方法及改进

1.1 传统的Craig-Bampton方法

根据对文献［4-5］的推导可得出动态子结构的模态坐标和物理坐标之间的变化关系为：

式（1）表示通过传统的Craig-Bampton固定边界模态综合法，用模态坐标的形式将弹性结构的形变体现出来。然而，这种模态分析法有其使用前提，即假设结构不存在大面积刚体运动，它所解决的是线性动力学问题。而在多体系统动力学问题中，部件相对于坐标系存在大面积运动，则此种方法不适合有大面积刚体运动的情形；进一步分析可知，传统的Craig-Bampton方法分析的模态是在静态缩聚条件下的结果［3］，并不能反应柔性结构的动态频率，从而其模态与频率无法对应起来，若要将此方法应用于多体动力学当中，就有必要对传统Craig-Bampton法作出合适的改进。

1.2 改进的Craig-Bampton方法

在多柔体系统中大量存在着刚柔耦合作用，因此，需要采用一些浮动标架来描述系统的运动状态，而约束模态中已经包括了刚体模态，因此，必要时需要去除刚体模态，此时就涉及模态缩减的问题，在此采用改进的模态缩减方法，使其能够适用于多柔体系统。

求解单个柔性体的动力学方程在Craig-Bampton模态坐标下所对应的无阻尼振动方程的特征值、特征向量：

由式（2）可得到相应的正则化模态，记为B，原来的模态可运用新的模态坐标表示：

将式（3）代入［6］，有：

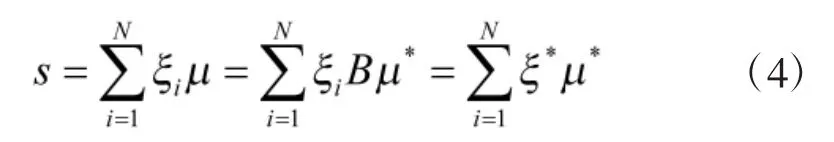
式中ξ*为具有原系统的主模态及约束模态所有属性的正交的C-B模态，它能反应边界作用以及高阶模态拟静力作用；μ*为C-B模态坐标。

通过上述方法改进，自由振动的无约束体的特征向量近似替代了正则化固定界面模态，从而成功去除了6个刚体运动模态。

2 发射装置刚柔耦合模型

2.1 发射装置组成及拓扑结构

倾斜发射地空导弹发射装置主要由车底盘、转台、起落架等部分组成。车底盘主要由车架、悬挂系统、车轮组、车轴等部分构成，由于车架跨度较大，将其设置为柔性体；车体两侧各安装的两个液压千斤顶，在实体模型中采用线性的弹簧阻尼器来模拟液压力，并将杆设为刚体。对转台进行几何简化处理后将其设置为柔性体；起落架由支架和起竖油缸组成，通过起竖油缸和耳轴与转台相连，将其作为柔性体处理。由于本文研究对象为弹箱系统，故将发射箱一并进行分析，发射箱固定在起落架上，将其设为柔性体，箱中的导弹与导轨间隙配合，通过闭锁器固定。发射装置拓扑结构如图1所示。

图1 发射装置拓扑图

支腿和起竖油缸采用柔性连接，二者的刚度和阻尼分别取45 000 N/mm，0.25 N·s/mm和30 000 N/mm，1.5 N·s/mm。

2.2 柔性体建模

根据发射装置转台、起落架、发射箱、车架的实体结构，首先在三维建模软件Pro/E中建立上述构件的三维实体模型，之后导入有限元分析软件ANSYS当中，对其进行有限元预处理，建立转台、起落架、发射箱和车架的有限元模型，并对其进行模态分析，完成后扩展前36阶模态，从而在不影响精度的同时减少了计算时间，最终形成模态中性文件并导入ADAMS中构成柔性体模型。

2.3 建立刚柔耦合模型

根据倾斜发射地空导弹发射装置的实际结构，在Pro/E中进行各个刚性构件的实体建模，之后通过中间转换格式，将模型逐一导入ADAMS中，进行装配，同时将上述各个柔性体模型也导入ADAMS中进行装配，最终建立的刚柔耦合动力学模型如图2所示。

图2 刚柔耦合动力学模型

模型中各构件的参数，如质量、惯量、质心位置、弹簧刚度、阻尼等数据来源于设计值或试验数据。

2.4 坐标系的设定

2.4.1 全局坐标系

该坐标系为右手坐标系，其Y轴垂直水平面指向上方；Z轴在水平面内，沿发射车车轴方向指向后方，坐标原点位于转台中心位置。

2.4.2 弹箱局部坐标系

该坐标系同为右手坐标系，其Y轴垂直于发射箱底面指向上方；Z轴平行于发射箱底面，沿导弹发射方向指向前方，坐标原点根据不同局部坐标系确定。

3 发射过程弹箱姿态仿真分析

3.1 发射过程载荷

3.1.1 发动机推力

发动机的推力使导弹产生加速度，也引起弹—架系统的振动［7］，推力载荷随时间变化，作用于发动机喷口中心，沿导弹轴线方向，为提高仿真精度，将发动机试车实测数据差值拟合，可得发动机推力曲线。

3.1.2 爆炸螺栓产生的脉冲激励

通过爆炸当量计算爆炸螺栓产生的脉冲激励［8］，爆炸螺栓的冲量是640 N·s，作用时间为2 ms，作用力位于发射箱前端面上的8个螺栓处，故平均每个螺栓受到大小为8 kN的冲击力。

3.1.3 燃气流作用力

发射过程中发射装置受到的来自于发动机尾部产生的燃气流冲击作用所形成的载荷难以通过实验测量得出［9］，根据燃气流畅的仿真分析结果，结合实际产生的燃气射流的流场参数，将燃气流作用力近似拟合为作用于发射箱质心上的3个方向上的力和力矩。

3.2 仿真结果分析

在进行仿真分析前，运用模态分析软件Hyper-Mesh对倾斜发射装置刚柔耦合模型进行模态分析，通过比较测量的试验频率，得到了模型频率与试验频率对照表，如表1所示。由表1可知，模型频率和试验测得频率相差不大，误差基本在±5%的范围之内，而且前6阶模态振型也基本相符，表明通过刚柔耦合的方式建立的模型是可信的。

表1 模型频率与试验频率对照表

将建好的倾斜发射装置刚柔耦合模型在ADAMS中建立相关约束，并施加各类载荷，文中选定发射条件为：方位角0°保持不变，高低角选取36°、48°、60°3个档位，设定仿真时长，对发射过程中弹箱姿态进行动力学仿真，比较在3种发射条件下，高低角的变化对于弹箱姿态的影响性，下页图3为3种条件下发射箱俯仰角（发射过程中发射箱相对初始位置的俯仰偏转）变化曲线。图4为3种条件下导弹相对于发射箱俯仰角（发射过程中导弹与发射箱之间的相对夹角在与发射车轴垂直的平面内的角度分量）变化曲线。

由图3可见：首先，不论以哪个高低角进行发射，导弹与发射箱二者处于约束期时，随着导弹的位移，导弹对发射箱作用力逐渐减小，发射箱逐渐抬头；随着导弹与发射箱进入半约束期直至导弹离轨出箱时，发射箱产生回弹。其次，对比3幅图可知，随着高低角的增大，发射箱的俯仰角变化越来越小，表明发射时的高低角度越大，发射箱的振动响应越小。

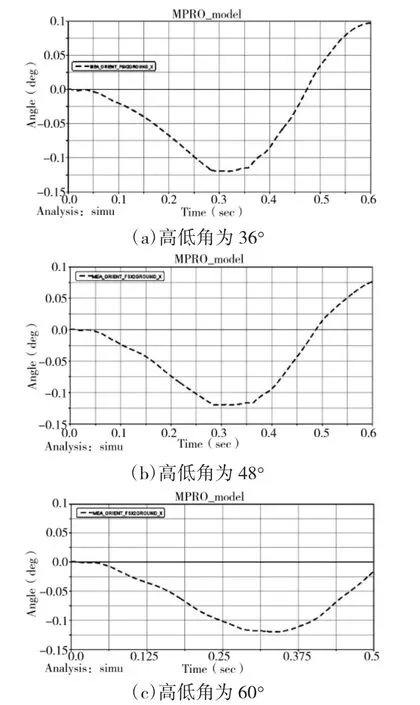
图3 发射箱俯仰角变化曲线

图4 导弹相对于发射箱俯仰角变化曲线

由图4可见：首先，导弹点火后直至与发射箱之间的倒数第2组适配器分离的时段内，弹箱之间只有轴向相对运动；之后适配器对导弹有一个相对弹箱局部坐标系Y轴向上的作用力，使导弹有一个低头力矩。其次，对比3幅图可知，随着角度的增大，导弹相对发射箱的俯仰角逐渐减小，表明高低角度越大，导弹姿态越稳定。

4 结论

运用改进Craig-Bampton方法处理复杂多体系统中存在的大范围刚体运动问题，首先建立了构件的柔性体模型，之后结合多刚体动力学，建立了系统刚柔耦合模型，并对发射过程中弹箱俯仰角度变化进行了仿真。结果表明，高低角为36°～60°区间内，在满足实际发射条件的情况下，应尽量选取较大高低角进行发射，从而能够有效减少发射过程中导弹和发射箱振动响应，以达到减小初始扰动，提高发射精度的目的。高低角超过60°后的导弹姿态及发射箱振动响应有待进一步研究。

［1］芮筱亭.多体系统发射动力学［M］.北京：国防工业出版社，1995.

［2］高星斗，白静，张平，等.发射箱车载倾斜发射过程下沉量影响因素研究［J］. 导弹与航天运载技术，2015，44（2）：58-62.

［3］张涛，刘相新，郑斌.基于模态综合法的发射过程刚柔耦合动力学研究［J］.导弹与航天运载技术，2009，38（6）：51-54.

［4］CRAIG R R，BAMPTON M C C.Coupling of substructures fordynamics analyses ［J］.AIAA Journal，1968，6（7）：1313-1319.

［5］殷学纲，陈淮，蹇开林.结构振动分析的子结构方法［M］.北京：中国铁道出版社，1991.

［6］ZHANG W Y，GAO J B，WANG C.Rigid-flexible coupling dynamic analysis of sub-launched vehicle during the vertical tube-exit stage［J］.Journal of Harbin Institute of Technology，2015，22（2）：26-33.

［7］姜毅，魏昕林，陈苗.发射动力学［M］.北京：北京理工大学出版社，2015.

［8］吴艳红，王晓晖，马斌捷.爆炸螺栓盒的爆炸模拟与冲击强度计算［J］.强度与环境，2007，34（6）：10-15.

［9］陈余军，姜毅.车载导弹发射过程姿态模拟［J］.弹道学报，2012，24（1）：102-106.

Missile and Launch Container Attitude Simulation of Incline Launching Vehicle in Launching Process

WANG Ding-nan，WANG Xue-zhi（School of Air and Missile Defense，Air Force Engineering University，Xi’an 710051，China）

In order to study the change of missile and launch container attitude in the process of incline launching vehicle’s launching，the key parts and components such as the frame，revolver，undercarriage and launch container are regarded as the flexible bodies and are merged into the multibody dynamics model of incline launching vehicle with the improved Craig-Bampton method，the rigidflexible coupling model of incline launching vehicle is established and proved，the conclusion of launching angle’s selection is obtained by different launching conditions’simulation of angle of pitch for missile and launch container.

incline launching，launching process，missile and launch container attitude

1002-0640（2017）10-0087-04

TJ768.2

A

10.3969/j.issn.1002-0640.2017.10.019

2016-08-25

2016-10-09

王玎楠（1992- ），男，河南洛阳人，硕士研究生。研究方向：发射动力学。