相控阵主动雷达导引头波形策略
2017-11-17蒋兵兵盛卫星张仁李韩玉兵马晓峰
蒋兵兵, 盛卫星, 张仁李, 韩玉兵, 马晓峰
南京理工大学 电子工程与光电技术学院, 南京 210094
相控阵主动雷达导引头波形策略
蒋兵兵, 盛卫星*, 张仁李, 韩玉兵, 马晓峰
南京理工大学 电子工程与光电技术学院, 南京 210094
针对高脉冲重复频率脉冲多普勒 (HPRF-PD) 体制的相控阵主动雷达导引头中存在的距离遮挡问题,设计了一种新的波形选择策略。首先,利用提出的脉冲重复频率(PRF)波形选择策略,离线计算得到距离对应PRF的波形查找表。然后,通过叉积自动频率控制环路滤波 (CPAFCLF) 算法预估下个相参处理间隔(CPI)导引头与目标间的径向相对速度,并联合提出的基于Sage-Husa带有速度预测的自适应“当前”统计模型 (SH-ACSMVP)算法得到的距离跟踪值,获得下个CPI的距离预测值。在跟踪机动目标场景中,相比于“当前”统计(CS)模型跟踪算法及基于“当前”统计模型的自适应无迹卡尔曼滤波 (CAUKF) 算法,本文算法得到的距离预测误差更小,误差收敛速度更快。根据此距离预测值从波形查找表中选择波形发射,作为下个CPI的发射波形,实现后续跟踪阶段的抗距离遮挡,提高目标跟踪性能。仿真结果表明了本文所设计波形选择策略的正确性及有效性。
相控阵; 雷达导引头; 波形策略; 脉冲多普勒; 距离遮挡; Sage-Husa算法
相控阵主动雷达导引头是精确制导技术的发展趋势[1-3],其中使用最普遍的一种工作体制是脉冲多普勒(Pulse Doppler, PD)。PD相控阵主动雷达导引头大多采用高脉冲重复频率(High Pulse Repetition Frequency, HPRF)波形进行发射,其具有测速不模糊、速度分辨率高和无杂波区范围大的特点[4]。在作战时,增强了导弹攻击低空目标,以及抗地、海杂波的能力[5-6]。
然而,由于HPRF-PD体制相控阵主动雷达导引头上的天线收发共用,为避免发射信号泄漏,当天线处于发射模式时,接收机关闭,由此引发了距离遮挡效应。导引头探测远距离目标,必定存在目标回波返回导引头时,其正处于信号发射模式的情形。此时,接收机关闭,无法收到目标回波,这种现象即为“距离遮挡”[7]。出现此种状况时,回波中信号能量急剧下降,致使导引头无法完成探测任务,影响跟踪性能。沈亮和李合新[8]研究了距离遮挡现象对导引头角跟踪系统以及制导系统的影响,并给出了各个系统抗遮挡的措施。
常用的抗距离遮挡技术有3种[9-10]:记忆跟踪算法、遮挡预判法和变重频法。记忆跟踪算法[11]利用滤波算法结合数据递推方法,在软件上解决遮挡问题。但当目标发生机动时,无法保证跟踪稳定性,甚至会丢失目标。陈付彬等[11]针对此问题,设计了记忆跟踪α-β滤波器与正常跟踪滤波器的切换机制,从实际微波暗室的测试结果看出,此机制提升了记忆跟踪算法抗距离遮挡的性能。遮挡预判法[9]通过已知遮挡期或无遮挡期的起始点,在得到弹目相对速度的精确值后,预判遮挡期的发生时刻,但由于进入遮挡期后,导引头接收通道关闭,无法获取该阶段的目标信息,故跟踪稳定性无法保证。变重频法[10]通过改变脉冲重复频率(Pulse Repetition Frequency, PRF),保证在整个检测范围内至少存在一个PRF没有被遮挡。此方法解决了HPRF-PD导引头中存在的距离遮挡问题,但其目的过于片面,并未从整个导引头系统考虑。导引头波形作为整个导引头信号处理系统的最前端[4,12],其特性对信号处理系统及信号处理算法的影响是不言而喻的。采用变重频法时,一方面,当PRF数目较多且差异较大时,对空时自适应处理(Space-Time Adaptive Processing, STAP)、检测前跟踪(Track Before Detection, TBD)等这类需同时对一组或多组相参处理间隔(Coherent Processing Interval, CPI)数据进行块处理的算法而言,由于回波数据规模不一致,需对数据块另行处理,此处增加的工作量是值得引起注意的。另一方面,即使各PRF大小接近,后续相应的信号处理算法将这几个重频值做近似相等处理,但引起的信号处理能力损失也是不可忽略的。变重频法的此缺点并不影响其在工程实际中的应用,其仍是目前最常用、最有效的抗距离遮挡方法。
变重频法有效抗距离遮挡的关键在于PRF切换准则的设定。现有变重频法所依据的PRF切换准则有3种[13-14]:第1种是根据回波信号强度的变化切换[13];第2种是循环依次切换PRF[15];第3种是利用弹目距离信息进行遮挡判断后切换[13,16]。从目标回波强度考虑,需要为消除弹目距离变化及目标起伏的影响提出可靠的判决准则,目前并无较好方案。循环依次切换PRF时,不需考虑弹目距离信息,几种PRF依次等间隔切换,总存在无遮挡的PRF,导引头据此PRF进行后续信号处理。该方法简单实用,但一方面,其信噪比(Signal-to-Noise Ratio,SNR)下降使得检测性能变弱;另一方面,对于导引头系统而言,其发射PRF恒定对后续信号处理系统的设计以及信号处理算法的优化是最为有利的,采用多种PRF依次发射,大大增加了信号处理模块的计算量。董胜波等[15]提出了采用4种PRF交替变换的方法,在解决距离遮挡的同时,也实现了解距离模糊。利用弹目距离信息进行遮挡判断的方法能彻底解决距离遮挡问题,但其要求测速和初始距离信息准确,还需要对距离测量值进行解模糊处理。具体来说,李建彬和夏桂芬[14]提出了基于简单查表的相关解距离模糊算法,提高了HPRF-PD雷达导引头的抗距离遮挡性能。何华兵等[16]对限定频率范围内的PRF进行分析,优选一组PRF,针对初始装订距离是否精确,分别设计不同的PRF切换方式,由导引头软件控制优选PRF组按照不同的方式切换工作,完成抗遮挡任务。郭玉霞等[17]通过对PRF的控制,使目标回波总是落入接收门中心位置,使导引头工作在无遮挡区。
研究以上变重频法可以看出,目前最好的PRF切换策略是利用弹目距离信息进行遮挡判断。王莹[13]、何华兵[16]等基于此提出了各自的方法。王莹等[13]的方法需利用传统的解距离模糊算法得到弹目距离信息,之后再进行波形切换,此方法存在两个缺点:① 传统的解距离模糊算法无法保证距离精度;② 未预测待发射PRF信号到达目标时刻的弹目距离,可能导致所选PRF仍产生距离遮挡效应。何华兵等[16]利用回波信号强度通过门限次数的统计值来判断目标是否进入遮挡区,无法保证切换准则的稳健性。
针对以上方法中的缺点,本文设计了一种简单的相控阵主动雷达导引头波形选择策略。根据距离不遮挡准则以及本文提出的PRF波形选择策略,预先确定一组重频集,并生成距离对应PRF的波形查找表。导引头工作时,首先根据地面站传来的初始弹目距离[10],在若干预定重频中选择一种满足距离不遮挡准则的PRF作为发射波形,经后续信号处理流程后得到模糊的距离测量值,通过模糊单元数与模糊距离测量值,可得不模糊的距离测量值[18]。使用叉积自动频率控制环路滤波 (Cross Product Automatic Frequency Control with Loop Filter, CPAFCLF) 算法[19],准确预估下个CPI弹目径向相对速度。再利用距离跟踪算法对此距离测量值进行滤波后,得到距离跟踪值。为得到下个CPI的距离预测值,本文提出了基于Sage-Husa[20]带有速度预测的自适应“当前”统计模型 (Sage-Husa-based Adaptive Current Statistical Model with Velocity Prediction, SH-ACSMVP) 算法,其距离预测性能相比于“当前”统计(CS)模型跟踪算法[21]及基于“当前”统计模型的自适应无迹卡尔曼滤波 (Current Statistical Model based Adaptive Unscented Kalman Filter, CAUKF) 算法[22]更优。用此弹目距离预测值在已离线完成的波形查找表中为下个CPI选择PRF作为发射波形,进行后续的信号处理,如此循环,直至跟踪阶段结束。
1 工作波形设计与分析
1.1 参数设计
主动雷达导引头的波形设计是决定系统测距测速性能的关键,主要需确定3个参数:发射PRF、发射占空比与接收占空比[4]。
HPRF-PD导引头测速不模糊,为使目标回波谱线落入无杂波区,发射PRF应满足[16]:
fPR≥fTmax+2fMmax
(1)
式中:fPR为发射PRF,Hz;fTmax=2VTmax/λ为目标多普勒频移最大值;fMmax=2VMmax/λ为旁瓣杂波多普勒频移最大值;VTmax和VMmax分别为目标和导引头速度最大值;λ为工作波长。
确定最小发射PRF后,考虑占空比[4]:根据导引头的最大探测距离,选取发射占空比;根据实际硬件的收发切换时间,选取接收占空比。
1.2 遮挡分析
图1给出了典型距离遮挡示意图。图中:τ为发射脉冲宽度;Tr为脉冲重复周期;Trt为接收切换到发射所需时延;Ttr为发射切换到接收所需时延;Trt与Ttr由硬件收发开关特性决定。
(2)
式中:τs为接收机输出回波脉冲宽度。
利用图1中的①、②两种距离遮挡情况,取回波最前面一个发射脉冲的起始时刻为0时刻,t为回波脉冲起始时刻,可得接收机输出回波脉冲宽度τs的表达式。式(2)中,t=rem(TMT,Tr),rem表示取余运算,TMT=2RMT/c,RMT为弹目相对距离,c为光速。实际工程中,更常用遮挡影响函数FD来描述距离遮挡效应。
定义τF=t/Tr=rem(2RMT/c,Tr)/Tr,FD=τs/τ,则有
(3)
从式(3)可以看出,FD反映了目标回波信号与发射脉冲的重合程度。其值越大,输出的回波脉冲宽度越宽,距离遮挡效应越弱;否则,输出的回波脉冲宽度越窄,距离遮挡影响越大。故本文采用遮挡影响函数来评价发射波形在给定距离范围内的距离遮挡状况。
图1 典型目标回波遮挡示意图
Fig.1 Typical scheme diagram of target echo eclipsing
2 CPAFCLF算法与SH-ACSMVP算法
2.1 CPAFCLF算法
目前,用于雷达及导引头中的速度测量及预测方法较多。文献[23]利用快速傅里叶变换(Fast Fourier Transformation,FFT)实现对雷达目标径向速度的测量;文献[24]在防空导弹导引头的建模仿真中,通过高低两个跟踪滤波器,利用FFT在频域形成了一个时刻套住目标的速度门,并由此实现对目标速度的测量跟踪。
在高动态环境中,锁频环常用于实现载波同步[19],其采用叉积自动频率控制(CPAFC)算法实现对载波频率的跟踪,此结构可以用于导引头速度跟踪环路中。
在导引头系统的速度通道中,设输入信号的频率为ω0,数控振荡器(Numerically Controlled Oscillator,NCO)内置的频率为ω1,则速度通道的信号与NCO混频后得到的Vs(k)=Ik+jQk,I路信号为Ik=Acos(ΔωkTs),Q路信号为Qk=A·sin(ΔωkTs),A为信号幅度,Δω=ω0-ω1,Ts为采样时间间隔。
根据叉积规则[19],可得
Vs(k)×Vs(k-1)=Ik-1Qk-Qk-1Ik=
Acos((k-1)ΔωTs)·Asin(kΔωTs)-
Asin((k-1)ΔωTs)·Acos(kΔωTs)=
A2sin(ΔωTs)≈A2ΔωTs
ΔωTs≪π/2
(4)
当ΔωTs≪π/2时,CPAFC算法的输出信号与频差Δω近似有线性关系,故可以用作鉴频器,将其应用在导引头的速度跟踪环路中,实现对目标多普勒频率的测量。
图2 CPAFCLF算法流程图
Fig.2 Flow chart of CPAFCLF algorithm
CPAFCLF算法流程如图2所示[19]。CPAFCLF算法[19]将二阶环路滤波器与CPAFC结构级联,由此形成速度预测环路。滑窗选取速度通道数据后送入CPAFC模块,得到鉴频输出结果,再送入环路滤波器中进行滤波,之后将得到的环路滤波输出与原先NCO的本地频率相加,更新为本次跟踪周期的NCO频率。如此循环,直至处理完所有数据点。将最后一次的NCO频率传出,作为此次速度通道信号对应的多普勒预测值,进而得到本次的速度预测值。
文献[23-24]中使用的速度测量方法均基于FFT。在低信噪比条件下,采用FFT实现的频率测量精度有限,而且与FFT点数有关。为了达到更高的精度,必须处理更多采样点,这会增大硬件信号处理平台的压力。但CPAFCLF算法中采用的CPAFC算法则不存在上述问题:一方面,相同的采样点数下,相比于FFT方法,其可以得到更高精度的速度测量值;另一方面,在低信噪比高动态环境中,文献[25]分析了CPAFC算法仍具备良好的鉴频精度。
此外,文献[23]中只使用了FFT,未添加跟踪滤波器;文献[24]在FFT处理后,尽管使用了高低跟踪滤波器,但得到的跟踪效果仍旧依赖于前级的FFT分辨率,实际上并没有达到数据滤波的目的。本文设计的CPAFCLF算法采用二阶环路滤波器作为CPAFC鉴频输出的后级,实现了数据滤波的功能,提高了数据的平稳性。
2.2 SH-ACSMVP算法
本文基于CPAFCLF算法[19]、Sage-Husa算法[20]及CS模型[21],提出了 SH-ACSMVP 算法。此算法通过CPAFCLF得到加速度测量值,避免了经典CS模型中要求对加速度极限a±max初值的设定,并利用此加速度值推导得到了自适应CS模型,同时求解了目标机动频率α的闭式解。将自适应的α值代入到距离跟踪模型中,得到自适应变化的过程噪声协方差矩阵。同时,考虑到距离跟踪模型中测量噪声协方差矩阵对跟踪性能也有较大影响,利用Sage-Husa算法实现了测量噪声协方差矩阵的自适应。由此使得距离跟踪模型能够自适应调整,大大提高了距离跟踪算法在机动目标跟踪场景中的适用性。
CS模型的数学模型为[21]
(5)
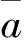
在HPRF-PD体制的相控阵导引头中,每个CPI的持续时间很短。因此,采用如式(6)所示的最简单方式即可得到第k个CPI的加速度测量值:
ak=(vk+1-vk)/T
(6)
式中:vk为第k个CPI的径向速度;T为每个CPI的时间。
CPAFCLF算法可以在第k个CPI得到第k+1个CPI的径向速度预测值,由此可得第k个CPI的加速度测量值ak。
设CPAFCLF算法得到的径向加速度值为am(t),则式(5)中的CS模型可重写为
(7)

将式(5)与式(7)对比,可得
(8)
对式(8)两边同时求导,可得
(9)
将式(9)代入式(7)的第2个等式中,可得
(10)
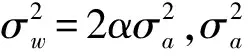
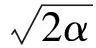
(11)
式中:x服从标准正态分布,即x~N(0,1)。
将式(10)与式(11)联立,得
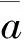
(12)
限定x的范围,并做出假设:x∈[-M,M], 其中M∈N+。
上述假设成立的概率为x落入区间[-M,M]的概率。考虑到x~N(0,1),当M≥4时,此假设成立的概率至少为99.994%。本文在此处作近似,认为:当M≥4时,x∈[-M,M]。
基于上述假设,令
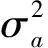
(13)
由此得到
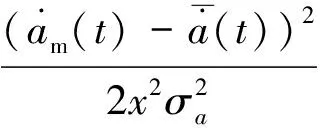
(14)

(15)
选择一个相应条件下的根作为α的值,当存在两个正根时,选择较小的根作为α的值;否则,无解,取α=0.01。
将自适应的α值代入到距离跟踪模型中,得到自适应变化的过程噪声协方差矩阵。
同时,SH-ACSMVP算法针对CS算法[21]中的测量噪声协方差矩阵,利用Sage-Husa算法[20]对其实施了自适应操作。
加入如式(16)的记忆衰减因子,实现估计过程中对最近数据的加权处理。
dk=(1-b)/(1-bk)
(16)
式中:b为记忆衰减因子,0 考虑记忆衰减因子后得到的测量噪声协方差矩阵Rk为 (17) 式中:vk为新息;Pk|k-1为滤波均方根误差矩阵;Hk为量测矩阵。 通过以上操作,SH-ACSMVP算法实现了距离跟踪模型中的测量噪声协方差矩阵以及过程噪声协方差矩阵的自适应,提高了准确跟踪机动目标的能力。 3.1 PRF波形选择策略 改变PRF,可以保证在检测距离范围内,至少有一种PRF可以实现不遮挡[13,16]。故基于式(3)中的遮挡影响函数FD,本文提出了一种PRF波形选择策略。 考虑到FD反映了目标回波信号与发射脉冲的重合程度,本文设定如下的距离不遮挡准则:当FD≤0.6时,回波脉冲处于遮挡状态;否则,回波未遮挡。 由此联合1.1节发射PRF的参数设计准则,利用遮挡影响函数及距离不遮挡准则来评估待选PRF波形在导引头整个工作距离内的遮挡性能。 遍历整个检测距离区间,可得各个弹目距离上的遮挡情况,如图3所示,0表示不遮挡,1表示遮挡。定义不遮挡区间为满足FD>0.6的距离范围,图3中的不遮挡区间为(Rh,Rj)。设当前的弹目距离值为Ri,Rh为Ri所处不遮挡区间起点对应的弹目距离值,Rj为Ri所处不遮挡区间终点对应的弹目距离值,则Ri到Rh、Rj的距离分别为r1=Ri-Rh,r2=Rj-Ri。定义不遮挡半径r0为当前距离值到其所处不遮挡区间端点的距离最小值,则r0=min{r1,r2}。 图3 距离遮挡示意图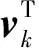
3 波形选择策略
Fig.3 Scheme diagram of range eclipsing
在某个给定距离下,当有多种PRF满足距离不遮挡准则时,若PRF对应的FD不相等,则选择FD值最大的PRF波形;否则,选取当前距离值下不遮挡半径r0最大的PRF作为此距离对应的PRF,存入距离对应PRF的波形查找表。
利用上述准则及1.1节中参数设计要求,选取出有NW个PRF的波形集,NW为波形集中波形的个数,此波形集满足在整个距离范围内满足距离不遮挡准则。
通过此PRF波形选择策略,最终得到一张距离对应PRF的波形查找表。
3.2 波形切换方法
首个满足距离不遮挡准则的PRF由地面站传来的初始弹目距离值选取[10]。经第1个CPI信号处理流程后得到模糊距离测量值。利用模糊单元数与模糊距离测量值,可得不模糊的距离测量值[18]:
Rt=NeRu+Rm
(18)
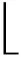
利用SH-ACSMVP算法对Rt进行滤波后,得到距离跟踪值。再联合CPAFCLF算法,利用式(19)[13,16]计算距离预测值,进而为下个CPI选择满足距离不遮挡准则的PRF作为发射波形,进行后续处理,如此循环,直至跟踪阶段结束。
(19)
基于卡尔曼滤波的距离跟踪算法,如CS算法[21]及CAUKF[22]都能给出下个CPI的预测值。但一方面,由于距离跟踪模型的局限性,导致距离跟踪算法中的状态转移矩阵无法随着目标运动的变化而变化;另一方面,这些距离跟踪算法中用于计算距离预测值的径向速度通常为当前CPI的距离变化率或为所测量得到的速度值,当目标发生大机动时,其会导致所得距离预测值的误差变大。本文中的SH-ACSMVP算法得到自适应变化的机动频率α,实现了距离跟踪模型的自适应,大大增强了其对机动目标跟踪场景的适用性。尽管式(19)的计算过程作了近似处理,但一方面,HPRF-PD导引头的CPI时间足够短;另一方面,利用CPAFCLF算法可以得到下个CPI较为精确的速度预测值,此种近似操作对距离预测值精度的影响完全可以忽略。
整个波形选择策略的步骤如下:
步骤1选取初始不遮挡PRF波形集。按照3.1节中的PRF波形选择策略,选择一组在给定的检测距离范围内满足距离不遮挡准则的波形集,得到一张距离对应PRF的波形查找表。
步骤2选择第一个CPI的发射PRF波形。由给定的初始弹目距离,从PRF波形集中选择当前距离对应的一种PRF作为发射波形发射。
步骤5重复步骤3、步骤 4,直至跟踪阶段结束。
4 计算机仿真
图4 仿真场景示意图
Fig.4 Scheme diagram of simulation scene
在图4所示的大地坐标系Oxyz中,以系统0时刻的目标位置为坐标系原点O′,导引头指向目标方向作为x′轴的正方向,O′z′轴位于包含O′x′轴的铅垂面内,且O′x′轴到O′z′轴为顺时针方向,O′y′轴与O′x′轴、O′z′轴构成右手坐标系O′x′y′z′。雷达导引头沿着O′x′轴正向以vM=300 m/s的速度匀速运动,目标沿着x′轴负方向以vT=200 m/s 的速度匀速运动,同时在x′O′y′、x′O′z′平面内分别做正弦运动,两者的空间运动轨迹及其轨迹在xOy、yOz、xOz平面内的投影如图4所示,导引头与目标的径向距离从8 km变化到1 km。
4.1 波形抗遮挡结果
根据3.1节的PRF波形选择策略,选取4种PRF组成发射波形重频集。τ=0.2 μs,Trt=0.12 μs,Ttr=0.04 μs,脉冲重复周期依次为Tr1=1.13 μs,Tr2=1.15 μs,Tr3=1.19 μs,Tr4=1.23 μs。
利用式(3)对此4种波形在1~10 km距离范围内,以1 m为间隔,对遮挡情况进行仿真,4种波形的遮挡影响函数如图5所示。图6(a)~图6(d)为4种PRF的距离遮挡情况,其中0表示不遮挡,1表示遮挡;图6(e)为采用变重频法得到的组合发射遮挡情况。可以看出,所选波形重频集在1~10 km范围内无遮挡。4种波形的遮挡PRF数分布如图7所示。
4.2 CPAFCLF性能
本文定义第k个CPI的速度预测误差为由CPAFCLF算法得到的速度预测值与第k+1个CPI的速度真实值之差,即
(20)
图5 4种波形的遮挡影响函数
Fig.5 Eclipse influence function of four waveforms
图8给出了CPAFCLF算法及文献[24]方法得到的速度预测仿真结果。可以看出,CPAFCLF算法仿真得到的速度预测误差在±0.05 m/s内,具有较好的精度。与文献[24]方法相比,一方面,CPAFCLF算法得到的径向速度误差快速收敛到稳态,而且测量误差很小,文献[24]方法由于没有数据滤波模块,得到的误差较大;另一方面,虽然真实径向速度的变化范围在逐渐扩大,但是CPAFCLF算法得到的预测误差并没有受到影响,而文献[24]方法则存在明显发散趋势。
图9中CPAFCLF算法得到的加速度测量曲线与仿真场景中真实的加速度曲线几乎重合,虽然加速度测量误差有部分小毛刺,但对后续SH-ACSMVP算法整体性能的影响不大。
为了进一步考量CPAFCLF算法性能,在图10 仿真场景中,弹目相对运动时间更长,增加了3种信噪比条件下的仿真对比。此处的信噪比指雷达导引头转入跟踪状态时刻速度通道信号的信噪比。图11~图13为信噪比为-7、1、9 dB场景的CPAFCLF性能曲线。可以看出,在不同信噪比条件下,CPAFCLF算法都能稳定地实现对径向速度的预测跟踪。在低信噪比条件下,其具有快速的误差收敛的特性。在高信噪比条件下,其得到误差性能直接达到稳态,误差可以忽略。另外,这3组实验也说明了CPAFCLF算法具有良好的信噪比动态范围,能够胜任雷达导引头跟踪目标的任务。
图6 4种PRF及其组合波形集的遮挡情况
Fig.6 Eclipse situation of four PRFs and their combinational set
图7 遮挡PRF数分布图
Fig.7 Distribution diagram of numbers of eclipsing PRFs
图8 CPAFCLF和文献[24]速度预测仿真结果
Fig.8 Simulation results of CPAFCLF and Ref.[24] velocity prediction
图9 加速度测量仿真结果
Fig.9 Simulation results of acceleration measurement
图10 CPAFCLF算法不同信噪比下性能的仿真场景示意图
Fig.10 Scheme diagram of simulation scene for CPAFCLF algorithm performance in different SNRs
图11 SNR=-7 dB条件下的CPAFCLF性能
Fig.11 CPAFCLF performance for SNR=-7 dB
图12 SNR=1 dB条件下的CPAFCLF性能
Fig.12 CPAFCLF performance for SNR=1 dB
图13 SNR=9 dB条件下的CPAFCLF性能
Fig.13 CPAFCLF performance for SNR=9 dB
4.3 弹目距离预测结果
图14为SH-ACSMVP算法在整个跟踪过程中计算得到的α变化曲线与弹目间径向加速度变化的对比曲线。从仿真结果可以看出,在径向加速度的峰值区域,α的值通常较大。加速度较大,则表明目标处于大机动状态,此时,对应的机动频率α也较大。从仿真得到的此种现象也证明了SH-ACSMVP算法的正确性。
为验证本文中SH-ACSMVP算法的性能,图15 为CS算法[21]、CAUKF算法[22]得到的距离预测曲线,以及SH-ACSMVP算法利用式(19)得到的距离预测曲线。从仿真结果中可以看出,相比于CS算法及CAUKF算法,SH-ACSMVP算法结合式(19)得到的距离预测误差初期快速下降到0.2 m,随后在0.2 m附近波动,并逐渐减小。CS算法的距离预测误差则相对较大。CAUKF算法初期预测误差下降速度较慢,跟踪后期与SH-ACSMVP算法的性能相仿,但由于使用了UKF算法,导致其计算复杂度是这3种算法中最高的。综合比较后,本文中的SH-ACSMVP算法更优。
图14 SH-ACSMVP算法中α与径向加速度对比
Fig.14 Contrast of α in SH-ACSMVP algorithm and radial acceleration
图15 距离预测误差
Fig.15 Range prediction error
3.1节中所得的距离对应PRF查找表的距离间隔为1 m,而且除去跟踪初期的10个CPI,整个跟踪流程的距离预测误差在1 m以内。因此,利用CPAFCLF算法联合SH-ACSMVP算法得到的距离预测值,加上离线得到的距离对应PRF查找表,本文所设计的波形选择策略可以准确地选取出一种不遮挡的PRF作为发射波形,为导引头信号处理系统后续正常运行提供保障。
与传统抗遮挡方法[13-17]相比,本文所提出的策略更加简单有效,主要表现在4个方面:① 离线确定距离对应PRF查找表,减少了导引头控制软件的工作开销;② 在发射时只使用一种PRF波形,应用更为简易,后续的信号处理算法计算量更小,硬件计算能力空闲度更高;③ 利用模糊单元数,无需解距离模糊,算法结构更加紧凑;④ 使用高精度的速度预测算法与距离跟踪算法,对机动目标场景的适用性更好,得到更准确的弹目距离预测值后选择无遮挡PRF,更彻底地解决了抗距离遮挡问题。
5 结 论
本文设计了一种新的相控阵主动雷达导引头抗距离遮挡的波形选择策略,有效地实现了抗距离遮挡。
1) 提出的CPAFCLF算法大大提高了对弹目径向相对速度的预测精度。
2) 基于CPAFCLF算法的SH-ACSMVP算法,可以得到更加准确的距离预测结果,确保本文中波形选择策略的有效性,有效地实现了抗距离遮挡。
3) 在场景合适的条件下,本文的波形策略同样可以应用在非相控阵导引头等平台中。
[1] 樊会涛, 闫俊. 相控阵制导技术发展现状及展望[J]. 航空学报, 2015, 36(9):2807-2814.
FAN H T, YAN J. Development and outlook of active electronically scanned array guidance technology[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(9): 2807-2814 (in Chinese).
[2] 王炼, 董胜波, 王秀君, 等. 毫米波宽带相控阵导引头关键技术综述[J]. 宇航计测技术, 2013, 33(3): 7-10.
WANG L, DONG S B, WANG X J, et.al. Review on the key technology of MMW wideband phased array seeker[J]. Journal of Astronautic Metrology and Measurement, 2013, 33(3): 7-10 (in Chinese).
[3] 唐怀民, 魏飞鸣, 宋柯. 相控阵雷达导引头技术发展现状分析[J]. 制导与引信, 2014, 35(3): 6-10.
TANG H M, WEI F M, SONG K. Analysis on technology development status quo of phased array radar seeker[J]. Guidance & Fuse, 2014, 35(3): 6-10 (in Chinese).
[4] 李林. 主动雷达导引头波形设计的分析与应用[C]//中国航空学会青年科技论坛. 北京: 中国航空学会, 2006: 267-273.
LI L. The analysis and application of the waveforms for active radar seeker[C]//Chinese Society of Aeronautics and Astronautics Youth Technology Symposium. Beijing: CSAA, 2006: 267-273 (in Chinese).
[5] 张凯, 张伟. PD雷达导引头海杂波回波信号模拟[J]. 雷达科学与技术, 2015, 13(2): 117-121.
ZHANG K, ZHANG W. Simulation of sea clutter echo signal in PD radar seeker[J]. Radar Science and Technology, 2015, 13(2): 117-121 (in Chinese).
[6] 董旭峰. 雷达导引头抗干扰技术研究[J]. 电子技术与软件工程, 2015, 4(6): 47.
DONG X F. Study of radar seeker anti-interference technology[J]. Electronic Technology and Software Engineering, 2015, 4(6): 47 (in Chinese).
[7] 李德纯. 主动雷达导引头工作波形设计及“遮挡”现象分析[J]. 制导与引信, 1999, 20(4): 7-13.
LI D C. Active radar seeker waveform design and eclipse phenomena analysis[J]. Guidance & Fuse, 1999, 20(4): 7-13 (in Chinese).
[8] 沈亮, 李合新. PD雷达导引头的遮挡现象及其处理方法[J]. 制导与引信, 2007, 28(1): 1-6.
SHEN L, LI H X. The eclipse phenomena and its solving method on PD radar seeker[J]. Guidance & Fuse, 2007, 28(1): 1-6 (in Chinese).
[9] 李庚泽, 顾村锋, 朱俊, 等. 雷达导引头三种抗遮挡技术的适用性分析[J]. 制导与引信, 2015, 36(1): 4-7.
LI G Z, GU C F, ZHU J, et.al. Applicable analysis of three anti-eclipse techniques for radar seeker[J]. Guidance & Fuse, 2015, 36(1): 4-7 (in Chinese).
[10] 吉炳奇. 毫米波雷达导引头抗距离遮挡技术研究[D]. 北京: 清华大学, 2004: 40-68.
JI B Q. The research of avoidance eclipse for mm-wave radar seeker[D]. Beijing: Tsinghua University, 2004: 40-68 (in Chinese).
[11] 陈付彬, 孙洪忠, 张军. 记忆跟踪在HPRF-PD雷达中抗距离遮挡的应用[J]. 制导与引信, 2008, 29(3): 42-47.
CHEN F B, SUN H Z, ZHANG J. Application of memory-tracking in HPRF-PD radar with range-eclipsing[J]. Guidance & Fuse, 2008, 29(3): 42-47 (in Chinese).
[12] 赵敏, 吴卫山. 主动雷达导引头工作波形研究[J]. 航空兵器, 2011, 47(4): 21-25.
ZHAO M, WU W S. Study on waveform design of active radar seeker[J]. Aero Weaponry, 2011, 47(4): 21-25 (in Chinese).
[13] 王莹, 苏宏艳, 朱淮城, 等. HPRF PD末制导雷达抗遮挡方法设计[J]. 微波学报, 2010, 31(1): 631-634.
WANG Y, SU H Y, ZHU H C, et al. Anti-range eclipse method designing for high PRF PD guiding radar[J]. Journal of Microwave, 2010, 31(1): 631-634 (in Chinese).
[14] 李建彬, 夏桂芬. 高重频PD雷达导引头抗距离遮挡技术[J]. 电讯技术, 2008, 48(10): 41-44.
LI J B, XIA G F. Avoidance eclipse for HPRF PD radar seeker[J]. Telecommunication Engineering, 2008, 48(10): 41-44 (in Chinese).
[15] 董胜波, 张文涛, 张晓峰, 等. 脉冲多普勒雷达导引头遮挡问题解决方法研究[J]. 宇航计测技术, 2008, 28(3): 1-4.
DONG S B, ZHANG W T, ZHANG X F, et.al. Research of solution to eclipse on pulse-Doppler radar seeker[J]. Journal of Astronautic Metrology and Measurement, 2008, 28(3):1-4 (in Chinese).
[16] 何华兵, 李文龙, 杨士义. 高重频雷达导引头变PRF抗遮挡方法设计[J]. 四川兵工学报, 2015, 36(5): 46-48.
HE H B, LI W L, YANG S Y. Avoidance eclipse using alterable PRF method designing for HPRF radar seeker[J]. Journal of Sichuan Ordnance, 2015, 36(5): 46-48 (in Chinese).
[17] 郭玉霞, 吴湘霖, 张德锋. 雷达导引头变重频抗遮挡算法设计[J]. 航空兵器, 2009, 45(3): 28-30.
GUO Y X, WU X L, ZHANG D F. Anti-eclipse algorithm design of radar seeker[J]. Aero Weaponry, 2009, 45(3): 28-30 (in Chinese).
[18] STIMSON G W. Introduction to airborne radar[M]. London: SciTech Pub, 1998: 153-157.
[19] JIANG B, SHENG W, ZHANG R, et al. CPAFC-based radar seeker velocity tracking loop design[C]//IEEE 4th International Conference on Control, Automation and Information Sciences (ICCAIS). Piscataway, NJ: IEEE Press, 2015: 432-435.
[20] SAGE A, HUSA G. Adaptive filtering with unknown prior statistics[C]//Proceeding of Joint Automatic Control Conference. Piscataway, NJ: IEEE Press, 1969: 760-769.
[21] ZHOU H, KUMAR K S P. A “current” statistical model and adaptive algorithm for estimating maneuvering targets[J]. Journal of Guidance, Control, and Dynamics, 1984, 7(5): 596-602.
[22] PENG X, YANG K, LIU C. Maneuvering target tracking using current statistical model based adaptive UKF for wireless sensor network[J]. Journal of Communications, 2015, 10(8): 579-588.
[23] ZENG Y, XU J, PENG D. Radar velocity-measuring system design and computation algorithm based on ARM processor[C]//Proceedings of the 8th World Congress on Intelligent Control and Automation. Piscataway, NJ: IEEE Press, 2010: 5352-5357.
[24] 倪震明, 陈长海, 刘俊. 防空导弹导引头建模与仿真[J]. 现代电子技术, 2012, 35(17): 25-29.
NI Z M, CHEN C H, LIU J. Modeling and simulation of air-defense missile seeker[J]. Modern Electronics Technique, 2012, 35(17): 25-29 (in Chinese).
[25] NATALI F D. Noise performance of a cross-product AFC with decision feedback for DPSK signals[J]. IEEE Transactions on Communications, 1986, 34(3): 303-307.
Waveformstrategyforphasedarrayactiveradarseeker
JIANGBingbing,SHENGWeixing*,ZHANGRenli,HANYubing,MAXiaofeng
SchoolofElectronicandOpticalEngineering,NanjingUniversityofScienceandTechnology,Nanjing210094,China
ThispaperconsiderstherangeeclipsingprobleminahighpulserepetitionfrequencypulseDoppler(HPRF-PD)phasedarrayactiveradarseeker.Anovelwaveformselectionstrategyisdesigned.Inthisstrategy,awaveformlookuptableconcerningrangeandpulserepetitionfrequency(PRF)isfirstlyobtainedoff-lineaccordingtothePRFselectionstrategyproposedinthisstudy.Amethodcalledcrossproductautomaticfrequencycontrolwithloopfilter(CPAFCLF)isthenutilizedtopredicttheradialvelocitybetweentheseekerandthetargetofnextcoherentprocessinginterval(CPI).Meanwhile,arangetrackingalgorithmcalledSage-Husa-basedadaptivecurrentstatisticalmodelwithvelocityprediction(SH-ACSMVP)isproposedtoobtainapredictedrangevaluefornextCPI.Comparedwithcurrentstatistical(CS)modelandcurrentstatisticalmodelbasedadaptiveunscentedKalmanfilter(CAUKF),theproposedmethodexhibitsabetterrangepredictingperformanceintrackingamaneuveringtarget,withsmallerpredictederrorandfastererrorconvergence.Withthispredictedvalue,thetransmittingwaveformisselectedfromthewaveformlookuptable,andarangeeclipsingproblemwillnotbegeneratedinthetrackingstage.Simulationshighlightthecorrectnessandeffectivenessofourproposedwaveformstrategy.
phasedarray;radarseeker;waveformstrategy;pulseDoppler;rangeeclipse;Sage-Husaalgorithm
2016-04-05;Revised2016-06-23;Accepted2016-07-18;Publishedonline2016-07-191706
URL:www.cnki.net/kcms/detail/11.1929.V.20160719.1706.002.html
s:NationalNaturalScienceFoundationofChina(11273017,61401207,61471196);NaturalScienceFoundationofJiangsuProvince(BK20140793);2015CollegeGraduateScientificResearchandInnovationPlanofJiangsuProvince(KYLX15_0375)
2016-04-05;退修日期2016-06-23;录用日期2016-07-18; < class="emphasis_bold">网络出版时间
时间:2016-07-191706
www.cnki.net/kcms/detail/11.1929.V.20160719.1706.002.html
国家自然科学基金 (11273017,61401207,61471196); 江苏省自然科学基金 (BK20140793); 江苏省2015年度普通高校研究生科研创新计划 (KYLX15_0375)
*
.E-mailshengwx@njust.edu.cn
蒋兵兵, 盛卫星, 张仁李, 等. 相控阵主动雷达导引头波形策略J. 航空学报,2017,38(4):320284.JIANGBB,SHENGWX,ZHANGRL,etal.WaveformstrategyforphasedarrayactiveradarseekerJ.ActaAeronauticaetAstronauticaSinica,2017,38(4):320284.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0215
TN958.2; V243.2
A
1000-6893(2017)04-320284-13
(责任编辑: 苏磊, 孙芳)
*Correspondingauthor.E-mailshengwx@njust.edu.cn
