任务期间考虑故障件报废无补给下的多级装备可用度评估
2017-11-17刘任洋李华李庆民
刘任洋, 李华, 李庆民
1.海军装备研究院, 北京 100037
2.海军工程大学 兵器工程系, 武汉 430033
3.海军工程大学 科研部, 武汉 430033
任务期间考虑故障件报废无补给下的多级装备可用度评估
刘任洋1, 李华2, 李庆民3,*
1.海军装备研究院, 北京 100037
2.海军工程大学 兵器工程系, 武汉 430033
3.海军工程大学 科研部, 武汉 430033
针对任务期间普遍存在的故障件报废问题,提出了一种适用于多等级多层级航空装备的可用度近似评估方法。首先通过忽略维修和运输时间将存在报废率的可修件等效为消耗件,然后分别通过后方保障中心对飞行基地备件量的分配以及下层级部件对上层级部件备件量的折算,将多等级多层级备件模型转化为单等级单层级模型,最后利用伽马分布的可加性得到整个保障系统的装备可用度。在实际算例中,通过与仿真结果的对比得出:当维修和运输时间较小或飞行基地备件配置充足时,本文提出的近似评估方法具有较高的精度。
任务期间; 多等级多层级; 故障件报废; 可用度; 备件方案
对于航空器材库存建模技术的研究,自Sherbrooke[1]于1968年提出备件管理多级(METRIC)模型以来,该模型得到不断拓展和改进,已发展成为包含Mod-METRIC[2]、Vari-METRIC[3]、Dyna-METRIC[4]等诸多模型在内的较为完善的理论体系。由于METRIC理论采用系统的分析方法,其操作简单、运算结果精度高,是目前解决可修复性备件多级库存问题的主流方法[5]。国外一些较为先进的备件优化工具,如瑞典的OPUS10、美国的VMETRIC等均将其作为核心模型和算法。
随着对备件保障问题研究的不断深入,在装备多维修级别、多层次结构的一般保障模式基础上,国内外学者结合串件拼修[6-8]、横向补给[9-12]、需求时变[13-14]等诸多保障工作中存在的实际问题,运用METRIC理论研究出了相应模型和算法,取得了不错的效果,进一步丰富和发展了METRIC理论。然而,尽管METRIC理论在装备多级库存建模中应用广泛,效果显著,但也有其无法解决的问题:首先,在时间维度上,METRIC理论假设保障周期任意长,着眼于解决装备从列装到退役整个寿命周期内总的备件规划问题,而对于短期任务下的备件方案评估问题,METRIC理论无法适用;其次,在空间维度上,METRIC理论所考虑的保障组织结构是包含外部供应商在内的完备的保障体系,在该体系下,备件即使报废也能从外部获得无限的补给[15]。而当装备在执行具体任务时,受条件制约可能只得到部分保障组织的支持,由于保障站点维修能力有限,存在故障件无法修复而又得不到外部补给(外部供应商的补给时间通常很长,短期任务无法考虑)的普遍情况,此时METRIC理论的基石——库存平衡方程不再成立,METRIC理论亦无法处理该类问题。
针对上述问题,在部队现有多等级多层级保障模式背景下,结合任务期间顶层保障站点修复概率小于1的实际情况,以整个保障系统装备可用度为指标,利用近似等效思想提出一种快速有效的备件方案评估方法。与METRIC侧重装备整个寿命周期备件的总体规划和评估问题不同,该方法着眼于具体任务阶段,因此可与METRIC理论相辅相成,为保障人员在装备服役不同阶段对备件方案和保障效能进行有效评估提供新思路。
1 问题描述及假设
以最基本的两等级两层级保障模型为例,更多等级更多层级的情况仍可按本文方法类推。考虑由一个后方保障中心和多个飞行基地构成的装备保障系统,如图1所示。装备部署在飞行基地,包含若干现场可更换单元(Line Replacable Unit,LRU)和车间更换单元(Shop Replacable Unit,SRU),如图2所示,各单元寿命均服从指数分布。
当某个飞行基地的装备发生故障,其原因是所属第1层部件LRU故障,若基地有该LRU备件,则将其替换故障件;若基地没有备件则发生1次备件短缺。故障LRU在飞行基地有一定维修概率,如果基地不能维修,则将其送往后方保障中心维修,同时向后方保障中心申领1项该备件。后方保障中心对故障LRU也存在一定维修概率,如果修复不了则作报废处理。在对LRU维修时,故障原因是其所属的SRU故障,如果现场有SRU备件,将其安装到LRU上即完成LRU的修理,如果现场没有SRU备件则会造成LRU的修理延误。SRU的送修、补给过程和LRU相同。
图1 多级保障结构
Fig.1 Multi-echelon support systems
图2 装备层次结构
Fig.2 Hierarchical structures of equipment
在上述保障过程描述之外还需做出以下几点假设和说明:
1) 所有备件需求率服从泊松分布。
2) 飞行基地均采用(S-1,S)库存策略,即缺少一件就向上级申领一件。
3) 各保障站点维修渠道无限,不会因为维修渠道被占满而出现维修等待的现象。
4) LRU的故障只是由其所属SRU之一故障所致,不考虑多个SRU同时故障的情况。
5) 备件在后方保障中心无法维修时则报废,不考虑外部补给的情况。
2 考虑故障件报废的多级库存系统建模
2.1 报废条件下可修复备件的消耗件近似等效
对于存在一定报废率的可修复单元,分析其从开始工作到最终报废经历的整个寿命周期,除了中间的若干次维修过程,该可修复单元与消耗件存在相似的寿命过程。两者的本质区别在于消耗件为连续工作直至报废,而可修单元为间断工作直至报废,间断工作是由维修时间造成。因此,如果忽略维修时间,可将存在一定修复概率的可修件近似等效为消耗件。
首先分析飞行基地各SRU在整个保障系统内的等效维修概率reij,该概率包含3部分内容:一是LRU、SRU均在飞行基地可修的概率;二是LRU在飞行基地可修,SRU虽在飞行基地不可修但在后方保障中心可修的概率;三是LRU在飞行基地不可修,但LRU、SRU均在后方保障中心可修的概率。即有
reij=r0jrij+r0j(1-rij)ri0+(1-r0j)r00ri0
(1)
式中:rij表示部件i在站点j的维修概率,i为备件种类编号,i=1,2,…,I,代表SRU,i=0代表LRU;j为保障站点编号,j=1,2,…,J,代表飞行基地,j=0代表后方保障中心。为了便于描述,如未特意强调,i仅代表SRU(即i=1,2,…,I),j仅代表飞行基地(即j=1,2,…,J)。
根据以上分析,在不考虑维修时间和运输时间的前提下,等效维修概率为reij的可修复单元SRUi可近似等效为平均寿命为MTBFeij的消耗件,MTBFeij即首项为MTBFi/(NjZ0Zi),公比为reij的等比数列之和:
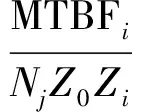
(2)
式中:MTBFi为SRUi平均寿命;Nj为装备在飞行基地j的配置数量;Z0和Zi分别为LRU和SRUi的机装数。则LRU的等效平均寿命为

(3)
需要说明的是,上述寿命等效过程虽然忽略了维修时间和运输时间,但通过大量实验表明,只要维修时间和运输时间之和不是太大或飞行基地LRU备件量配置充足时,该近似等效合理可行。
2.2 多级保障站点备件量的单级等效
在实现飞行基地消耗件寿命等效基础上,考虑后方保障中心备件量分配问题,即对各飞行基地所能向后方保障中心“竞争”到的备件量进行“事先”评估和分配,从而将两级保障结构等效为单级。
对于飞行基地j上的第项备件,在(S-1,S)库存策略下,其从后方保障中心分配所得备件比例kij为自身需求率λij与所有飞行基地总需求率λi0之比,即
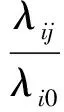
(4)
则在考虑后方保障中心备件量分配下,飞行基地j第项备件的等效备件量为
Seij=Sij+kijSi0i=0,1,…,I
(5)
式中:Si0、Sij分别为后方保障中心和飞行基地j第i项备件的配备数量。
至此,由后方保障中心和飞行基地构成的多等级保障系统被完全等效为仅包含各飞行基地在内的单级保障系统。在该系统下,飞行基地j包含等效寿命为MTBFe0j的LRU可修件以及等效寿命为MTBFeij的SRUi消耗件,其等效备件量分别为Se0j和Seij。
2.3 多层级部件备件量的单层级等效
由多层级部件的维修过程知,由于下层级的子备件SRU完全用于维修故障的母体部件LRU,若能提前对所配SRU备件共能维修成功的对应故障LRU件数进行有效评估,就可实现SRU备件向LRU备件的等效折算,从而将多层级可修复备件转化为仅包含LRU的单层消耗件。
飞行基地j上LRU发生故障由所属的SRUi故障导致的条件概率为
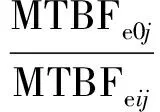
(6)
则一次对故障LRU维修所消耗的SRUi的备件数量为
(7)
将SRUi的备件消耗量等效折算为LRU的备件增加量,即
(8)
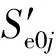
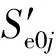
步骤2装备发生一次故障,消耗一个LRU备件,利用SRUi备件对其维修产生新LRU备件,得到当前LRU的累积备件增加量和可用数量分别为
图3 等效顶层LRU备件数量计算流程
Fig.3 Calculation process of number of spares for equivalent LRU in top indenture
Sleft_j=Sleft_j-1+ΔSe0j
步骤3更新当前各SRUi的备件数量:Seij=Seij-ΔSeij
步骤4如果可用LRU数量Sleft_j≤0,算法结束,得到等效LRU备件数量:
否则转入步骤2继续迭代。
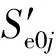
3 可用度评估模型
装备可用度是评价备件方案好坏、评估装备保障效能的常用指标,其定义为装备期望工作时间与总任务时间之比。
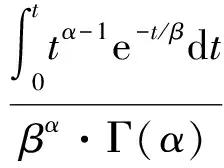
(9)

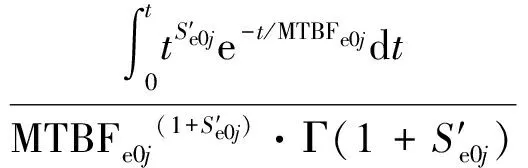
(10)
对于由多类LRU构成的装备,一般假设各LRU之间的可靠性结构为串联结构,由串联系统性质可知,飞行基地j装备可靠度为各LRU部件可靠度之积:
(11)
式中:l为LRU类别;Rlj(t)为LRUl可靠度函数,由式(10)得到。
在任务时间T内,装备可用度为装备的平均可靠度,由此得到飞行基地j的装备可用度为
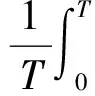
(12)
对于整个保障系统而言,全部装备的可用度为各飞行基地装备可用度的加权平均[17],设装备在各基地的部署数量为Nj,则有
(13)
4 算例分析
在一次为期1 000 h的训练任务中,由一个后方保障中心(编号为0)和两个飞行基地(编号分别为1、2)组成的保障系统对某航空装备开展实时保障。装备的组成结构如图2所示,在飞行基地的部署数量分别为[8,5],备件由后方保障中心运送至两个飞行基地的时间均为50 h。现要求对该装备在任务期间的可用度进行评估,备件的相关可靠性、维修性参数以及在各站点的配备数量如表1所示。其中:Trij表示部件i在站点j的维修时间;Zi为部件i的装机数。
利用本文近似等效方法得到整个保障系统的装备可用度评估结果为0.982 5。为了验证该方法的正确性,采用MATLAB平台构造仿真模型与近似结果进行对比。仿真次数设为2 000,分别统计每次仿真各飞行基地的累计停机时间Tdj,则可用度为(1-Tdj/T),取2 000次仿真所得的可用度均值作为最终输出结果。运行仿真程序,得到保障系统装备可用度评估结果为0.968 3,与仿真结果相比,近似结果的相对误差为1.46%,在合理的误差范围内。为了进一步研究近似方法的误差变化情况,使任务时间T以500 h为间隔,在[1 000,10 000] h区间内取值,分别得到近似方法和仿真方法的评估结果曲线如图4(a)所示(A表示保障系统可用度,Oj表示运输时间),图中两条曲线基本重合,相对误差最大发生在T=1 500 h 时,其值为2.61%,而当T>3 000 h时,近似结果与仿真结果基本吻合。单次仿真的主要流程如图5所示,因此,尽管本文近似方法忽略了维修时间和运输时间,但所得结果都在合理误差范围内,由此可知,存在维修、运输时间不一定会产生维修和运输延误,即使产生了维修和运输延误,延误后果也不一定很严重(延误时间短,对可用度影响不大)。

表1 备件和保障站点相关参数Table 1 Corresponding parameters of spare parts and support sites
为了进一步探究维修、运输时间对近似方法精度的影响,将两个飞行基地的运输时间Oj从算例中的50 h分别增加到100 h和150 h,得到近似结果和仿真结果如图4(b)、图4(c)所示。随着运输时间的增加,近似结果不断偏离仿真结果,相对误差最大值由2.61%分别增加到3.94%和5.99%。这与理论分析的结果一致,由于运输时间的增加使得产生运输延误的风险加大,增加了运输延误时间,导致仿真的可用度结果不断降低从而与近似结果的偏差逐渐拉大。大量实验表明:当各部件的平均维修时间与运输时间之和在装备平均故障间隔时间的一半以内时(算例中运输时间取值在50 h和100 h下满足该条件),近似方法均能保证一定的精度。需要说明的是,虽然当维修时间和运输时间超过一定阈值,近似方法误差较大,无法对某些具有高精度评估要求的场合实施准确的定量评估,但近似结果与仿真结果曲线变化趋势一致,此时近似方法完全可以作为定性评估备件方案好坏和可用度高低的有效手段。
图4 不同运输时间下的可用度评估结果对比
Fig.4 Comparison of results of availability with different transportation time
图5 单次仿真的主要流程
Fig.5 Main process of single simulation
此外,影响近似方法精度的关键是维修和运输延误,而维修和运输延误不仅与维修、运输时间有关,也与站点备件配置量有关。尤其对于装备使用现场(飞行基地)的LRU备件,其对延误时间的影响最大。以上述算例中误差最大的运输时间均为150 h的情况为例,将LRU1、LRU2在飞行基地的备件配置量Slj分别从1取到3,所得结果如图6所示。可以看出,即使运输时间较大,随着飞行基地LRU配置量的增加,近似结果不断逼近仿真结果,最大误差由8.45%降低至3.97%,最后达到2.01%。当Slj=3时,近似结果基本与仿真结果重合。这是因为即使维修、运输时间较大,但装备使用现场充足的LRU备件量给维修和运输中的备件赢取了时间,从而降低甚至抵消了由于维修和运输产生的延误,使近似方法能对可用度进行准确的评估。
图6 不同飞行基地LRU备件配置量下的可用度评估结果对比
Fig.6 Comparison of results of availability with different numbers of spares of LRU in the base
5 结 论
在部队现有多等级多层级保障模式背景下,结合航空装备在执行任务期间普遍存在的故障件报废问题,利用等效思想提出了一种快速有效的可用度近似评估方法。通过大量的仿真对比实验得到以下结论:
1) 当各部件的平均维修时间与运输时间之和较小(小于装备平均故障间隔时间的一半)或飞行基地LRU备件配置充足(2个以上)时,发生维修和运输延误的风险较小,延误即使发生了,延误后果并不严重,本文近似方法可以对可用度进行准确的定量评估。
2) 当各部件的平均维修时间与运输时间之和较大(大于装备平均故障间隔时间的一半)且飞行基地LRU备件配置量较少(1个或不配)时,发生维修和运输延误的风险很大,并能造成一定的延误后果,此种情况下本文近似方法可对可用度的高低、备件方案的好坏作定性评估。
在实际执行任务期间,为了保证任务的顺利完成通常对装备有着较高的可用度保障要求,导致飞行基地LRU备件数量较大的情况较为常见,为近似方法的使用创造了条件。
[1] SHERBROOKE C C. METRIC: A multi-echelon technique for recoverable item control[J]. Operations Research, 1968, 16(2): 122-141.
[2] MUCKSTADT J. A model for a multi-item, multi-echelon, multi-indenture inventory system[J]. Management Science, 1973(20): 472-481.
[3] SHERBROOKE C C. VARI-METRIC: Improved approximations for multi-indenture multi-echelon availability models[J]. Operations Research, 1986, 34(2): 311-319.
[4] HILLESTAD R J. Dynametric: Dynamic multi-echelon technique for recoverable item control: R-2785-AF [R]. Santa Monica: RAND Corporation, 1982.
[5] FRANCESCO C, GIULIO D G, MASSIMO T. Multi-echelon, multi-indenture spare parts inventory control subject to system availability and budget constraints[J]. Reliability Engineering and System Safety, 2013, 119: 95-101.
[6] SALMAN S, CASSADY C R, POHL E A, et al. Evaluating the impact of cannibalization on fleet performance[J]. Quality and Reliability Engineering International, 2007, 23(4): 445-457.
[7] 李羚伟, 张建军, 张涛, 等. 面向任务的拼修策略问题及其求解算法[J]. 系统工程理论与实践, 2009, 29(7): 97-104.
LI L W, ZHANG J J, ZHANG T, et al. Mission oriented cannibalization policy problem and its solving algorithm[J]. Systems Engineering—Theory & Practice, 2009, 29(7): 97-104 (in Chinese).
[8] 罗祎, 阮旻智, 李庆民. 多级维修供应下不完全串件系统可用度评估[J]. 系统工程与电子技术, 2012, 34(6): 1182-1186.
LUO Y, RUAN M Z, LI Q M. Evaluation of availability for incomplete cannibalization system under multi-echelon maintenance supply[J]. Systems Engineering and Electronics, 2012, 34(6): 1182-1186 (in Chinese).
[9] OLSSON F. An inventory model with unidirectional lateral transshipments[J]. European Journal of Operations Research, 2010, 200(3): 725-732.
[10] LORENZO T, STEFANO S. Reducing the mean supply delay of spare parts using lateral transshipments policies[J]. International Journal of Production Economics, 2011, 133(1): 182-191.
[11] 张光宇, 李庆民, 李华. 零备件的多点库存单向转运模型与算法[J]. 航空学报, 2013, 34(5): 1092-1100.
ZHANG G Y, LI Q M, LI H. Unidirectional transshipment model and algorithm in multi-location inventory of spare part[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(5): 1092-1100 (in Chinese).
[12] 刘任洋, 李庆民, 李华. 基于横向转运策略的可修件三级库存优化模型[J]. 航空学报, 2014, 35(12): 3341-3349.
LIU R Y, LI Q M, LI H. Optimal model of three-echelon inventory for repairable spare parts with lateral transshipments[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(12): 3341-3349 (in Chinese).
[13] LAU H C, SONG H W, SEE C T, et al. Evaluation of time-varying availability in multi-echelon spare parts systems with passivation[J] . European Journal of Operational Research, 2005, 170(1): 91-105.
[14] 王睿, 彭英武, 李庆民, 等. 面向动态任务的作战单元两等级两层级可修复备件优化[J]. 系统工程与电子技术, 2013, 35(4): 761-769.
WANG R, PENG Y W, LI Q M, et al. Dynamic mission-oriented two-echelon and two-indenture repairable spare parts optimization for combat units[J]. System Engineering and Electronics, 2013, 35(4): 761-769 (in Chinese).
[15] RUAN M Z, LUO Y, LI H. Configuration model of partial repairable spares under batching ordering policy on inventory state[J]. Chinese Journal of Aeronautics, 2014, 27(3): 558-567.
[16] 甘茂治, 康建设, 高崎. 军用装备维修工程学[M]. 2版. 北京: 国防工业出版社, 2010: 44-46.
GAN M Z, KANG J S, GAO Q. Military equipment maintenance engineering[M]. 2nd ed. Beijing: National Defense Industry Press, 2010: 44-46 (in Chinese).
[17] SHERBROOKE C C. Optimal inventory modeling of system: Multi-echelon techniques[M]. 2nd ed. Boston: Artech House, 2004: 31-32.
Evaluationforavailabilityofmulti-echelonmulti-indentureequipmentwithscrapoffailurepartsduringthemission
LIURenyang1,LIHua2,LIQingmin3,*
1.NavalAcademyofArmament,Beijing100037,China2.DepartmentofWeaponryEngineering,NavalUniversityofEngineering,Wuhan430033,China3.OfficeofResearch&Development,NavalUniversityofEngineering,Wuhan430033,China
Fortheproblemofscrapoffailurepartsexistingwidelyduringthemission,anapproximateevaluationmethodforavailabilityofmulti-echelonmulti-indentureaviationequipmentisproposed.Repairablespareswithscrapareconvertedtonon-repairablesparesbyomittingrepairandtransportationtime.Thesparesarethenassignedfromtherearsupportcentertotheflightbaseandareconvertedfromlowerintohigherindenturesuccessively,sothatthemulti-echelonmulti-indenturesparemodelisconvertedintothesingle-echelonsingle-indentureones.TheavailabilityofthewholesupportsystemisobtainedbasedontheadditivepropertyofGammadistribution.Acomparisonoftheactualexamplewiththesimulationresultsshowsthattheapproximatealgorithmcanbeofhighprecisionwhenthevaluesofrepairandtransportationtimearenottoogreatorthesparesoftheflightbasearesufficient.
duringthemission;multi-echelonmulti-indenture;scrapoffailureparts;availability;configurationplanofspareparts
2016-05-24;Revised2016-07-13;Accepted2016-10-08;Publishedonline2016-10-141350
URL:www.cnki.net/kcms/detail/11.1929.V.20161014.1350.006.html
s:NationalDefensePre-researchFoundationofChina(51304010206,51327020105)
2016-05-24;退修日期2016-07-13;录用日期2016-10-08; < class="emphasis_bold">网络出版时间
时间:2016-10-141350
www.cnki.net/kcms/detail/11.1929.V.20161014.1350.006.html
国防预研项目基金 (51304010206,51327020105)
*
.E-maillicheng001@hotmail.com
刘任洋, 李华, 李庆民. 任务期间考虑故障件报废无补给下的多级装备可用度评估J. 航空学报,2017,38(4):220465.LIURY,LIH,LIQM.Evaluationforavailabilityofmulti-echelonmulti-indentureequipmentwithscrapoffailurepartsduringthemissionJ.ActaAeronauticaetAstronauticaSinica,2017,38(4):220465.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0268
V125.7; E911; TJ761.1
A
1000-6893(2017)04-220465-09
(责任编辑: 苏磊)
*Correspondingauthor.E-maillicheng001@hotmail.com
