切深对椭圆超声振动切削机理的影响

张翔宇， 张德远， 隋翯， 姜兴刚

北京航空航天大学 机械工程及自动化学院， 北京 100083

切深对椭圆超声振动切削机理的影响

张翔宇， 张德远*， 隋翯， 姜兴刚

北京航空航天大学 机械工程及自动化学院， 北京 100083

以椭圆超声振动切削为研究对象，通过理论分析，有限元仿真和切削实验，研究了切深变量对其切削过程中机理的影响。指出在微小的切深条件下，刀尖钝圆影响不可忽略，其切削过程表现出微细切削特性。一方面，基于微细切削理论，建立了正交椭圆超声振动切削运动学和力学模型，将切削区分为后刀面回弹区、刀尖犁切区、刀尖剪切区和前刀面摩擦区四个区域，并依次对四个区域内不同切深条件下各个切削分力进行计算分析。另一方面，对切削过程进行有限元仿真和切削实验。其结果表明：当切深小于最小切削厚度时，切削过程主要为刀具后刀面的回弹挤压与摩擦和刀尖钝圆的犁切作用，不产生切屑，切深抗力大于主切削力；当切深大于最小切削厚度并逐渐增大时，刀尖剪切和切屑与前刀面的挤压与摩擦作用逐渐凸显并成为主要切削方式，此时主切削力逐渐超过切深抗力并迅速增大。

椭圆超声振动； 切深； 刀尖钝圆； 微细切削； 最小切削厚度

现代航空制造领域内存在着大量的难加工材料，如不锈钢、钛合金、镍基高温合金和复合材料等。克服其较差的切削加工性能，提高其加工精度和效率一直为航空制造领域中的重要目标。而椭圆振动切削自从提出[1]后，经过二十多年的高速发展，已成为克服上述困难的有效方法而广泛应用于各类难加工航空材料[2-3]的精密切削加工中。

研究人员对椭圆超声振动切削过程进行的大量研究指出其具有大幅度降低切削力、改善工件已加工表面质量和抑制加工颤振等优势[4-7]。而为了进一步揭示获得上述优势的原因，切削实验、切削过程建模和有限元仿真等深入研究工作也得到了同步的开展。切屑的产生过程和瞬时切削力的波形同步对比研究表明，除周期性分离带来的空切特性之外，椭圆振动切削独有的摩擦力反转特性是切削力相比传统振动切削更大幅度下降的原因[8]。在对瞬时切削力建模的过程中，切削过程多被简化为平面剪切模型，剪切角和摩擦角的动态变化使其切削过程不同于普通切削[9-12]。有限元方法的使用，同时能够对上述椭圆超声振动切削过程中的特有现象进行分析和验证[13]。

然而，以上对工艺效果和切削原理的研究均是建立在将刀具假想为理想锋利模型的基础上。但是在实际切削过程中，刀具切削刃并非是理想锋利刀刃，而是在刀尖处存在一个钝圆。又由于椭圆超声振动切削为精密切削加工方法，其切深与刀尖钝圆半径处在同一数量级中，因此刀尖钝圆对切削过程中切削机理的影响不应再被忽略。但考虑到刀尖钝圆影响的椭圆超声振动研究中，切削力模型通过利用刀具切削面积作为中间量，设定一个相关系数来建立[14-15], 其切削过程又无法准确刻画小切深条件下的微细切削特性[16]。由此可见，大量文献对椭圆超声振动切削机理和微细切削特性的研究是孤立和分开的，而使用微细切削理论来研究椭圆超声振动切削机理的文献尚不多见。

本文基于微细切削的特性，研究了变化的切深对正交椭圆超声振动切削机理的影响，通过建立正交椭圆超声振动切削运动模型和力学模型，并辅以有限元仿真方法，揭示了不同切深条件下正交椭圆超声振动切削过程中的微细切削现象和主切削力与切深抗力关系的变化规律。最后通过切削实验，验证所建立的模型和有限元仿真的有效性。

1 理论分析

1.1 运动模型

图1为椭圆振动切削示意图，图中：v为刀具切削线速度；x、y和z轴分别表示切深、进给和切削速度方向；A和B分别为刀具在x和z方向的振幅。刀具沿着图示轨迹产生周期性的振动，其为z方向上的匀速直线运动、正弦简谐振动和x方向上的正弦简谐振动合成。和传统振动切削类似，只要当刀具的切削速度小于理论极限速度v=2πfB[17]时便会产生断续切削，实现刀具和工件的周期性分离现象，f为刀具振动频率。此外，由于在x方向上同时存在超声振动，因此椭圆超声振动切削在切深小于2A时，刀具和工件同样也会出现周期性的分离现象。

图2为正交椭圆振动切削刀具轨迹，图中：t1和t2分别为刀具切入和切出工件时刻；T为一个振动周期；t为切削过程中任意时刻；P点为此时工件表面的位置，其与椭圆振动切削参数相关；ap(t)为切深；φ为瞬时速度角。

图1 椭圆振动切削
Fig.1 Elliptical vibration cutting

图2 正交椭圆振动切削刀具轨迹
Fig.2 Tool locus in orthogonal elliptical vibration cutting

椭圆超声振动发生在zx平面内。在一个振动周期内，刀具相对工件的运动方程为

(1)

式中：z(t)和x(t)分别为刀具在z和x方向上的位移大小；ψ为两方向振动相位差。

刀具的分离特性用占空比(Duty Cycle, DC)来衡量，其指在一个振动周期内，净切削时间所占的比值，表达式为

(2)

由于刀具在x方向存在振动，因此ap(t)的计算公式为

ap(t)=x(t)-xPt1≤t≤t2

(3)

式中：xP为P点位置坐标。

瞬时速度角定义为刀具的运动轨迹和z方向的夹角，其计算式为

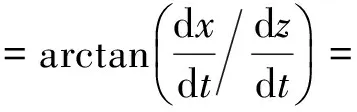
(4)

刀具的实际前角γ和实际后角α，随着刀具瞬时速度角的变化而变化，其表达式为

(5)

式中：γ0为刀具的名义前角；α0为刀具的名义后角。

1.2 力学模型

由于椭圆超声振动的引入，正交椭圆超声振动切削为一个变速和变切深的切削过程。其中变化的切深对切削状态有着显著的影响。本节在综合已有的普通微细切削力学模型[18-19]的基础上，将切深按照椭圆超声振动的形式加以变量化，从而得出正交椭圆超声振动切削的瞬时切削力与平均切削力模型。

传统切削力模型将切削区分为刀尖剪切区、前刀面摩擦区和后刀面回弹区。然而，不可忽略的刀尖钝圆使得切削过程中存在一个刀尖犁切区，如图3所示。图中：Ⅰ为后刀面回弹区；Ⅱ为刀尖犁切区；Ⅲ为刀尖剪切区；Ⅳ为前刀面摩擦区；σ1、σ2、σ3和σ4分别为以上各切削区中的正应力；τ1、τ2、τ3和τ4分别为以上各切削区中的切应力；apmin为最小切削厚度，其定义和计算公式由Son等[20]给出；δ(t)为工件后刀面回弹量；Lf(t)为切屑与刀具的接触长度；Ls(t)为剪切区沿前刀面直线段长度；θp(t)为刀尖犁切区范围积分上限；θe为刀具和工件接触的最低点B和最小切削厚度临界点C之间的夹角；θk(t)为剪切区沿前刀面圆弧范围角。

切削过程中的主切削力FC和切深抗力FP的表达式为

(6)

式中：FCi和FPi(i=1,2,3,4)分别为上述4个区域中的主切削力和切深抗力。

下面将分别对引入了变化切深后，4个区域中切削情况和切削力进行讨论。

图3 正交切削刀具受力示意图
Fig.3 Diagram of stress distribution on orthogonal cutting tool

Ⅰ区AB段(图3(a))中，由于刀尖钝圆的存在，切削后的工件材料在经过了Ⅱ区的犁切熨压作用后沿着圆弧CB流向后刀面，并发生弹性回复，从而产生挤压和摩擦后刀面的现象。通过切削动力学分析后得出后刀面正应力和切应力的表达式为

(7)

式中：σs为工件材料的屈服强度。

后刀面摩擦系数μc为切应力与正应力之比，其表达式为

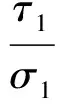
(8)

则普通微细切削后刀面回弹区的主切削力和切深抗力分别为

(9)

式中：ω为正交切削宽度；δ0为工件最大弹性回复量，其是一个和切深相关的变化量，当切深ap(t)≤δ0时，刀具不产生切屑，刀尖钝圆在工件表面划过，工件只发生弹性挤压变形，在刀具离开工件表面后，挤压弹性变形完全回复，其回弹量等于切深，即δ0=ap(t)，当切深ap(t)>δ0时，刀尖钝圆在工件表面划过，弹性变形和塑性变形均有发生，在刀具离开工件表面后，只发生弹性回复，其回弹量为工件的最大弹性回复量，即δ(t)=δ0；刀具的后角为式(5)中的实际后角。将修改后的回弹量，后角的计算公式代入式(9)即可得到后刀面回弹区的瞬时主切削力与切深抗力。

Ⅱ区BC段(图3(b))中，工件材料受到刀尖钝圆对工件的犁切熨压作用。其正应力和切应力的表达式为

(10)

式中：μs为剪切区摩擦系数。

不考虑切深的动态变化，普通切削刀尖犁切区的主切削力和切深抗力分别为

(11)

式中：rg为刀尖钝圆半径。

当切深ap(t)>apmin时，犁切区范围为0～θe，即式(11)中的积分上下限，因此其可计算此时的瞬时主切削力和切深抗力；当切深ap(t)≤apmin时，切削仅为犁切熨压过程，不产生切屑，其积分上限为θp，由几何关系可知：

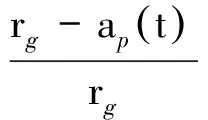
(12)

则此时犁切区瞬时主切削力和切深抗力分别为

(13)

Ⅲ区(图3(b))中，工件发生剪切塑性变形，产生断裂和切屑，其塑性变形过程可简化为幂强化模型σ=Cεn的形式，σ为正应力；C为幂强化模型中的应力系数；ε为正应变；n为幂强化模型中应变强化指数。则其正应力和切应力的表达式为

(14)

式中：φ为剪切角，由MERCHANT剪切公式可知：

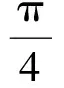
(15)

式中：β为摩擦角，和剪切区摩擦系数μs相关，其表达式为

β=arctanμs

(16)

剪切区的范围由于切深的变化，也是一个动态变量。当ap(t)≤rg(1+sinγ)时，其为一段圆弧，终止角度θk，由几何关系可得：

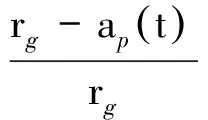
(17)

则按照微细切削切削力计算公式计算可得瞬时主切削力和切深抗力分别为

(18)

当ap(t)>rg(1+sinγ)时，剪切区为一段圆弧和一段直线 ，由几何关系可知θk的表达式为

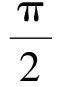
(19)

而剪切区沿前刀面直线段长度可以记作：

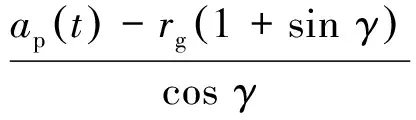
(20)

(21)

(22)

定义阶跃函数p(x)：

(23)

记λ=p(ap(t)-rg(1+sinγ))为一个剪切区判定函数，综合式(18)和式(22)可得到刀尖剪切区瞬时主切削力和切深抗力分别为

(24)

IV区(图3(a))中，其正应力和切应力的表达式为

(25)

由微细切削切削力计算公式可知瞬时主切削力和切深抗力分别为

(26)

切屑与刀具的接触长度表达式[21]为

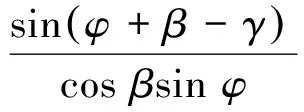
(27)

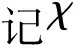
(28)

综上4个切削区所述，在一个完整的振动周期T内，瞬时切削力FC,P(t)表达式为

(29)

(30)

1.3 模型分析

当最大切深分别为2、5、8 μm 3种情况时，4个切削分力按照切削力学模型，参照表1和表2中所示参数，得出的结果如图4所示。刀具的钝圆半径约为10 μm，根据最小切削厚度公式计算其最小切深约为3 μm。因此当最大切深为2 μm，即小于最小切削厚度时，切削过程仅为后刀面的回弹挤压与摩擦和刀尖钝圆的犁切作用，并不发生剪切和切屑与前刀面摩擦作用，此时平均切深抗力大于平均主切削力。当最大切深为5 μm，即超过最小切削厚度时，切削过程中开始出现剪切和切屑与前刀面摩擦作用，此时平均主切削力显著增大，并与平均切深抗力基本持平。当最大切深继续增大为8 μm时，切削过程中剪切和切屑与前刀面摩擦作用显著增强，其切削力增幅远远大于后刀面的回弹挤压与摩擦和刀尖钝圆犁切作用所产生的切削力，此时平均主切削力大于平均切深抗力，其切削过程逐渐过渡到能用传统切削模型描述。

表1 刀具与切削参数Table 1 Tool and cutting parameters

表2 材料参数Table 2 Material parameters

图4 不同切深下切削力对比示意图
Fig.4 Diagram of cutting force in each cutting zone with different depth of cut

2 切削仿真与实验

为了验证变化的切深对正交椭圆超声振动切削4个切削分力的影响并说明切削过程中的微细切削特性，有限元仿真方法因其通过合理的参数设置能够模拟切削过程中每一时刻的切削现象，首先被应用[22]。它有效地克服了因现有测量手段无法实测和观察具有20 kHz的超声频振动切削过程所带来的研究困难。随后进行相应的切削实验，通过对平均切削力的采集，一方面验证切削过程中的微细切削特性，另一方面也验证了所建立切削力学模型和切削仿真的有效性。

2.1 切削仿真与实验设置

Deform-3D是研究金属塑性变形的一款通用仿真软件。使用其中包含的切削仿真模块[23-24]，建立如表1所示的刀具和切削参数。切削工件选用材料库中的45号钢。刀具设置为刚体，因此无需完全画出，刀具长度为6 mm，刀具运动轨迹按照式(1)设置。工件设置为弹塑性体，宽度1.5 mm，整体做固定位置约束。仿真时间为一个振动周期0.000 05 s，仿真步数为200步。

图5 实验工件剖面
Fig.5 Cross-section of workpiece

采用实验室自制超声刀具进行正交椭圆超声振动切削实验。超声刀具由自制电源激振，产生在x和z方向上振幅均为5 μm，相位差90°，频率f=20 000 Hz的椭圆超声振动。刀片选用山特维克TCMT06T102系列标准刀片，刀具参数见表1，用固定螺栓固定在刀槽中，将三角形刀片的长边用作切削刃。刀具装夹在Kistler9254A测力仪上，测量结果通过Kistler Type 5070电荷放大器放大后由数字采集器采集。实验工件为45钢，为了保证切削实验过程中的系统稳定性，其设计如图5所示，在直径40 mm的圆柱工件内，预先切出一个深度为5 mm，宽度为3.5 mm的沟槽，其内外径分别为30 mm和37 mm，从而得到1.5 mm厚的薄壁。切削参数见表1，实验前通过试切，使其待切削平面平面度小于1 μm。实验参数设置同仿真参数。实验平台为HARDINGE HLV-H超精密车床，其主轴跳动误差小于1 μm，整体如图6所示。

图6 实验平台示意图
Fig.6 Diagram of experiment platform

2.2 仿真与实验结果

图7 切削有限元仿真示意图
Fig.7 Diagrams of cutting finite element simulation

对最大切深分别为2、5、8 μm 3种情况的切削有限元仿真结果如图7所示。结果表明：当最大切深为2 μm时，在图7(a)中，刀具在整个切削过程中仅在工件表面划过，并未产生切屑，工件的受力变形区仅为刀尖钝圆与工件接触的犁切部位；当最大切深为5 μm时，在图7(b)中，刀具刚刚切入时，由于切深小于最小切削厚度，同样不产生切屑，工件的受力变形区和图7(a)中所示类似，但当切深逐渐增大超过最小切削厚度时，刀具对工件的剪切作用产生，同时产生切屑，此时工件的受力变形区沿着整个刀尖钝圆分布；当最大切深为8 μm时，在图7(c)中，当切深超过最小切削厚度时，剪切和切屑与前刀面摩擦作用明显，此时工件的受力变形区主要集中在剪切区和前刀面的摩擦区。由此可知，仿真的切削过程与切削力学模型所揭示的切削过程相吻合。

此外，有限元仿真与切削力学模型计算所得的瞬时切削力如图8所示。有限元仿真，切削力学模型计算所得和切削实验所得的平均切削力如表3所示。结果表明，切削力波形与数值的有效性得到验证。

在切削力学模型的建立过程中，因主要凸显变化切深对切削过程的影响，在刀具应力分析和摩擦条件设定上进行了简化处理。而有限元仿真虽是一种便捷的研究手段，但其也是一种理想化后的数值处理方法。因此通过实验的手段去研究变化切深对切削过程的影响是后续需要开展的工作，而其中的重难点便是准确的采集到超声频的瞬时切削力信号，其是揭示切削机理的重要因素。

图8 切削瞬态力波形
Fig.8 Waveform of transient cutting force

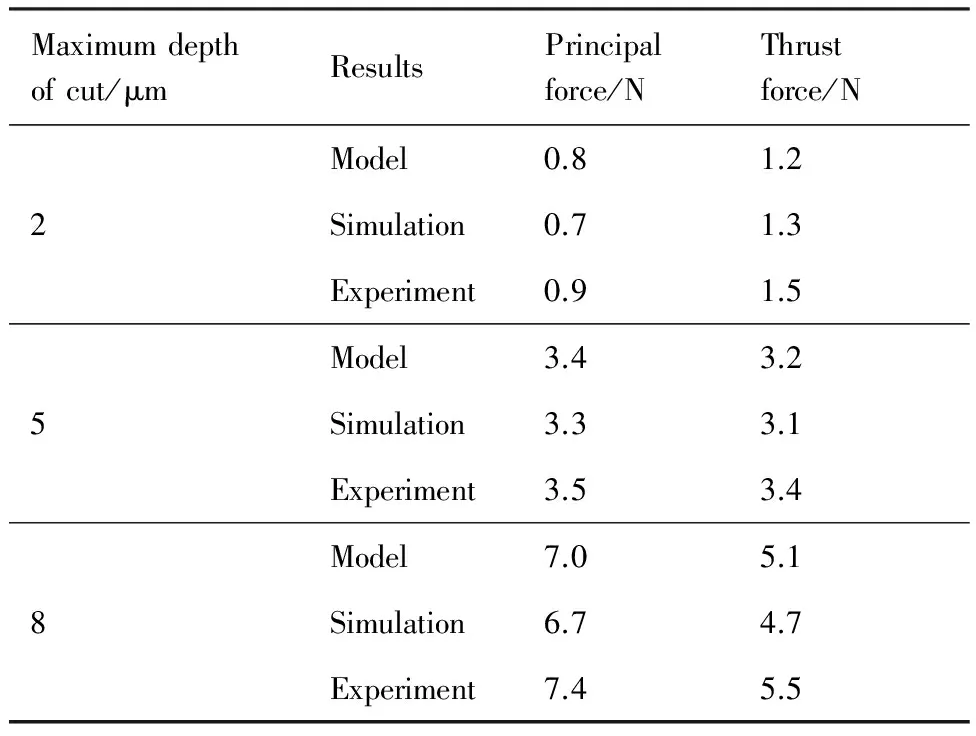
表3 平均切削力Table 3 Average cutting force

3 结 论

1) 变化的切深使得正交椭圆超声振动切削过程中存在微细切削特性。

2) 当切深小于最小切削厚度时，切削过程主要为刀具后刀面的回弹挤压与摩擦和刀尖钝圆的犁切作用，不产生切屑，此时切深抗力大于主切削力。

3) 当切深大于最小切削厚度并逐渐增大时，刀尖剪切和切屑与前刀面的挤压与摩擦作用逐渐凸显并成为主要切削方式，此时主切削力逐渐超过切深抗力并迅速增大。

[1] MORIWAKI T, SHAMOTO E. Ultrasonic elliptical vibration cutting[J]. Annals of the CIRP-Manufacturing Technology, 1995, 44(13): 31-34.

[2] PATIL S, JOSHI S, TEWARI A, et al. Modeling and simulation of effect of ultrasonic vibrations on machining of Ti6Al4V[J]. Ultrasonics, 2014, 54(2): 694-705.

[3] XU W, ZHANG L. Ultrasonic vibration-assisted machining: principle, design and application[J]. Advances in Manufacturing, 2015, 3(3): 173-192.

[4] MA C X, SHAMOTO E, MORIWAKI T. Study on the thrust cutting force in ultrasonic elliptical vibration cutting[J]. Materials Science Forum, 2004, 471-472: 396-400.

[5] 季远, 李勋, 张德远, 等. 超声椭圆振动精密切削[J]. 航空制造技术, 2005(4): 92-95.

JI Y, LI X, ZHANG D Y, et al. Precision ultrasonic elliptical vibration cutting[J]. Aeronautical Manufacturing Technology, 2005(4): 92-95 (in Chinese).

[6] 隋翯, 张德远, 陈华伟, 等. 超声振动切削对耦合颤振的影响[J]. 航空学报, 2016, 37(5): 1696-1704.

SUI H, ZHANG D Y, CHEN H W, et al. Influence of ultrasonic vibration cutting on mode-coupling chatter[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(5): 1696-1704 (in Chinese).

[7] ZHANG X Q, LIU K, KUMAR A, et al. A study of the diamond tool wear suppression mechanism in vibration-assisted machining of steel[J]. Journal of Materials Processing Technology, 2014, 214(2): 496-506.

[8] SHAMOTO E, MORIWAKI T. Study on elliptical vibration cutting[J]. Annals of CIRP-Manufacturing Technology, 1994, 43(1): 35-38.

[9] SHAMOTO E, SUZUKI N, HINO R. Analysis of 3D elliptical vibration cutting with thin shear plane model[J]. Annals of CIRP-Manufacturing Technology, 2008, 57(1): 57-60.

[10] ZHANG X Q, KUMAR A, RAHMAN M, et al. An analytical force model for orthogonal elliptical vibration cutting technique[J]. Journal of Manufacturing Processes, 2012, 14(3): 378-387.

[11] NATEGH M J, RAZAVI H, ABDULLAH A. Analytical modeling and experimental investigation of ultrasonic-vibration assisted oblique turning, Part I: Kinematics analysis[J]. International Journal of Mechanical Sciences, 2012, 63(1): 1-11.

[12] RAZAVI H, NATEGH M J, ABDULLAH A. Analytical modeling and experimental investigation of ultrasonic-vibration assisted oblique turning, Part II: Dynamics analysis[J]. International Journal of Mechanical Sciences, 2012, 63(1): 12-25.

[13] 于海鹏. 基于有限元法的椭圆振动切削机理研究[D]. 北京： 北京化工大学, 2014: 11-36.

YU H P. Research on elliptical vibration cutting mechanism based on finite element method[D]. Beijing: Beijing University of Chemical Technology, 2014: 11-36 (in Chinese).

[14] BAI W, SUN R L, GAO Y, et al. Analysis and modeling of force in orthogonal elliptical vibration cutting[J]. International Journal of Advanced Manufacturing Technology, 2015, 83(5): 1-12.

[15] 杨毅青, 张斌, 刘强. 铣削建模中多种切削力模型的分析比较[J]. 振动工程学报, 2015, 28(1): 82-90.

YANG Y Q, ZHANG B, LIU Q. Analysis and comparison of various cutting force models in the milling process simulation[J]. Journal of Vibration Engineering, 2015, 28(1): 82-90 (in Chinese).

[16] KIM J D, KIM D S. Theoretical analysis of micro-cutting characteristics in ultra-precision machining[J]. Journal of Materials Processing Technology, 1995, 49(3): 387-398.

[17] BREHL D E, DOW T A. Review of vibration-assisted machining[J]. Precision Engineering, 2008, 32(3): 153-172.

[18] 方瑞. 微细车铣切削力建模及切削试验研究[D]. 沈阳: 沈阳理工大学, 2013: 11-48.

FANG R. Research on cutting forces modeling and test of micro turn-milling[D]. Shenyang: Shenyang Ligong University, 2013: 11-48 (in Chinese).

[19] 石文天. 微细切削技术[M]. 北京： 机械工业出版社， 2011: 36-60.

SHI W T. Micro machining technology[M]. Beijing: China Machine Press, 2011: 36-60 (in Chinese).

[20] SON S M, LIM H S, AHN J H. Effects of the friction coefficient on the minimum cutting thickness in micro cutting[J]. International Journal of Machine Tools and Manufacture, 2005, 45(4-5): 529-535.

[21] OXLEY P L B, HASTINGS W F. Minimum work as a possible criterion for determining the frictional conditions at the tool/chip interface in machining[J]. Philosophical Transactions of the Royal Society B Biological Sciences, 1976, 282(3): 565-584.

[22] ANAND R S, PATRA K. Modeling and simulation of mechanical micro-machining-a review[J]. Machining Science and Technology, 2014, 18(3): 323-347.

[23] 柳柏魁, 林正英. 基于Deform-3D钻削加工三维有限元仿真[J]. 工具技术, 2015, 49(7): 43-47.

LIU B K, LIN Z Y. Three dimensional FEM simulation of drilling based on software Defrom-3D[J]. Tool Engineering, 2015, 49(7): 43-47 (in Chinese).

[24] 张蓉蓉, 赵先锋, 李长虹, 等. 基于Deform-3D的铝合金7075车削力模型的研究[J]. 组合机床与自动化加工技术, 2016(6): 59-62.

ZHANG R R, ZHAO X F, LI C H, et al. Analysis of the cutting force modeling of aluminum alloy 7075 based on Deform-3D[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2016(6): 59-62 (in Chinese).

Influenceofdepthofcutonellipticalultrasonicvibrationcuttingmechanism

ZHANGXiangyu,ZHANGDeyuan*,SUIHe,JIANGXinggang

SchoolofMechanicalEngineeringandAutomation,BeihangUniversity,Beijing100083,China

Theinfluenceofthedepthofcutontheellipticalultrasonicvibrationcuttingmechanismisanalyzedthroughtheoreticalmodel,finiteelementsimulationandcuttingexperiment.Itisfoundthatwhenthedepthofcutissmall,theinfluenceoftheroundedcuttingedgemustbetakenintoconsideration,andthecuttingprocessrevealsthemicro-machiningcharacteristics.Thekinematicsmodelanddynamicsmodelfororthogonalellipticalultrasonicvibrationcuttingareestablishedbasedonthemicro-machiningtheory.Intheproposedmodels,thecuttingtoolisfirstlydividedintofourcuttingzonestheelasticrecoveryzoneontheflankface,theploughingzoneontheroundedcuttingedge,theshearingzoneontheroundedcuttingedge,andtool-chipfrictionzoneontherakeface.Thecuttingforceineachzoneisthencalculated.Finiteelementsimulationsofthecuttingprocessandcuttingexperimentsarealsoconducted.Simulationresultsshowthatwhenthedepthofcutislessthantheminimumcuttingthickness,thecuttingprocessisdominatedbyelasticrecoveryandfrictionontheflankfaceandploughingoftheroundedcuttingedge,withoutchipgeneration,withthethrustcuttingforcebeinggreaterthantheprincipalcuttingforce.However,whenthedepthofcutexceedstheminimumcuttingthicknessandkeepsincreasing,theeffectsofroundedcuttingedgeshearingandtool-chipfrictionontherakefacegraduallytakethedominantplaceduringthecuttingprocess,whiletheprincipalcuttingforceexceedsthethrustcuttingforceandincreasesrapidly.

ellipticalultrasonicvibration;depthofcut;roundedcuttingedge;micro-machining;minimumcuttingthickness

2016-06-28；Revised2016-07-25；Accepted2016-08-08；Publishedonline2016-08-171424

URL：www.cnki.net/kcms/detail/11.1929.V.20160817.1424.004.html

HeilongjiangProvinceApplicationTechnologyResearchandDevelopmentPlan(GA12A402)

2016-06-28；退修日期2016-07-25；录用日期2016-08-08； < class="emphasis_bold">网络出版时间

时间：2016-08-171424

www.cnki.net/kcms/detail/11.1929.V.20160817.1424.004.html

黑龙江省应用技术研究与开发计划 (GA12A402)

＊

.E-mailzhangdy@buaa.edu.cn

张翔宇， 张德远， 隋翯， 等． 切深对椭圆超声振动切削机理的影响J． 航空学报,2017,38(4):420567.ZHANGXY,ZHANGDY,SUIH,etal.InfluenceofdepthofcutonellipticalultrasonicvibrationcuttingmechanismJ.ActaAeronauticaetAstronauticaSinica,2017,38(4):420567.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0231

V261.92

A

1000-6893(2017)04-420567-09

(责任编辑： 李世秋)

＊Correspondingauthor.E-mailzhangdy@buaa.edu.cn