麦克斯韦滚摆运动规律的理论研究*
2017-11-16储若超张锐波
储若超 张锐波
(浙江大学城市学院信息与电气工程学院 浙江 杭州 310015)
麦克斯韦滚摆运动规律的理论研究*
储若超 张锐波
(浙江大学城市学院信息与电气工程学院 浙江 杭州 310015)
证明了滚摆在运动过程中势能、平动动能和转动动能是相互转化的,而总机械能是守恒的规律;推导出滚摆运动至最底端平动动能、转动动能的表达式,以及与总能量之关系,并根据自做滚摆参数计算出其结果.
麦克斯韦滚摆 质心加速度 机械能守恒 能量分配
将麦克斯韦滚摆自最低点向上沿一个方向对称绕线至合适高度,再自由释放,滚摆会在重力作用下,向下平动与转动.在运动过程中,滚摆的势能、平动动能和转动动能的总和保持不变.
如图1所示,为自制麦克斯韦滚摆实验仪,滚摆铜轴两端对称处用尼龙线悬挂于支架上,滚摆盘采用塑胶材料,可视为刚体.设摆轴质量为m,滚摆盘质量为摆轴质量n倍(即nm),则滚摆总质量为(n+1)m,滚摆铜轴半径r,滚摆盘半径R,是摆轴半径的n′倍,则R=n′r.

图1 麦克斯韦摆轮示意图
1 任意位置滚摆运动质心加速度推导
下面计算滚摆在运动过程中质心加速度aC,由质心运动定理列出滚摆平动方程
(n+1)mg-T=(n+1)maC
(1)
由刚体的转动定律列出滚摆的转动方程
Tr=Jβ
(2)
又质心在任意位置的瞬时加速度与角加速度的关系
aC=rβ
(3)
其中,T为滚摆牵引绳子张力,aC为滚摆平动加速度,J为滚摆转动惯量,β为滚摆转动角加速度.滚摆转动惯量等于滚摆铜轴转动惯量与滚摆盘转动惯量之和


(4)
解式(2)~(4)得

(5)
由式(1)、(5)得

则滚摆向下运动过程中任意时刻质心加速度为

(6)
2 滚摆运动过程中机械能守恒
如图2所示,1为滚摆绕线至最上端(即势能最大位置),3为运动至最低端(即势能为零位置),2为滚摆下落过程的任意位置.设滚摆在任意位置的机械能总量为
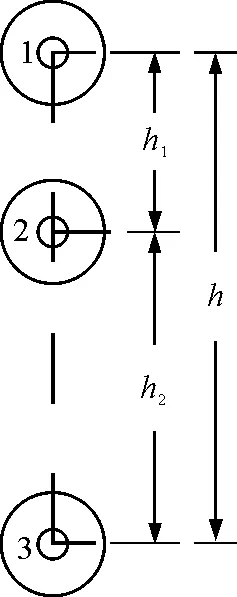
图2 原理分析示意图
E=Ep+Ek
(7)
在1位置时,Ek1=0,有
Ep1=(n+1)mgh
(8)
在2位置时,势能为
Ep2=(n+1)mg(h-h1)
(9)
(10)
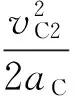
(11)
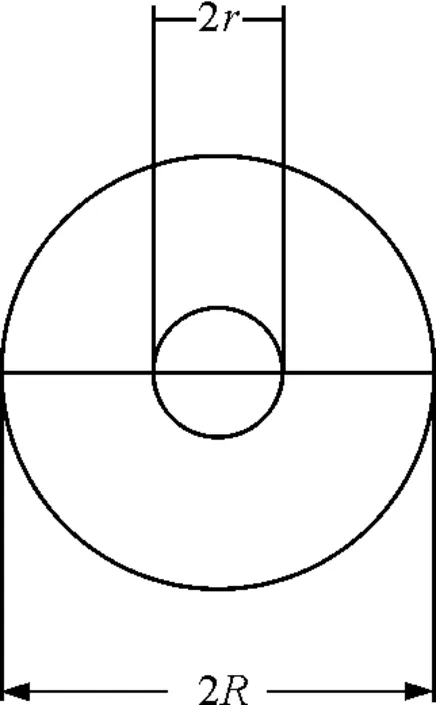
图3 摆轮与摆轴半径关系
滚摆自位置1到位置2时滚摆所具有的势能

(12)
滚摆下降至2位置处时,平动动能与转动动能的和为
(13)
式中ω为滚摆运动至位置2时,相对质心的角速度,vc2=ωr.
则有
(14)
E=Ep2+Ek2=

(15)
由式(15)可知,滚摆在位置2所具有的平动动能与转动动能之和,正好等于滚摆在位置1所具有的势能,即滚摆在运动过程中总能量保持不变.
3 滚摆运动过程中各部分能量分配关系
当滚摆运动至最低位置(即在位置3),该位置动能与总机械能、动能中的平动动能、转动动能和总机械能的数量关系.设滚摆运动至最低点势能Ep3=0,势能全部转化为平动动能与转动动能,总机械能为
E=Ek3+Ep3=Ek3=
(16)
其中,vC3为滚摆运动至最低点质心速度,ω3为滚摆相对轴心角速度;滚摆平动动能为
(17)
转动动能为


(18)
平动动能与总机械能之比为

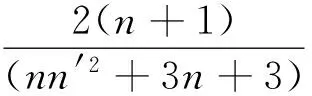
(19)
转动动能与总机械能之比为

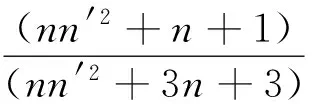
(20)
根据所制作的麦克斯韦滚摆相关参数:滚摆的总质量260.51 g,其中摆轴质量28.03 g;摆盘质量232.48 g;摆轮直径14.270 cm,铜轴直径0.649 2 cm.依据该仪器相关参数可得:n=8.294(摆盘质量与摆轴质量之比),n′=21.981(摆盘半径与摆轴半径之比),若选择麦克斯韦滚摆运动至最低位置时,可得平动动能与总能量、转动动能与总能量之比分别为0.002 62和0.995 4.由此可见,滚摆运动至最低点时,其能量主要是转动动能.
1 顾建中.力学教程.北京:人民教育出版社,1980
2 周衍柏.理论力学教程.北京:高等教育出版社,1986
TheoryStudyontheMotionLawoftheMaxwellRollPendulum
Chu Ruochao Zhang Ruibo
(College of Information and Electrical Engineering,College of City,Zhejiang University,Hangzhou,Zhejiang 310015)
This paper proves that the roll,the potential energy in the process of movement of translational energy and rotational energy is transformed into each other,and the total mechanical energy is conserved law;rolling pendulum movement to the end,the expression of kinetic energy of rotational kinetic energy is derived,and the relationship with the total energy,and according to the self rolling parameters calculated the result.
Maxwell roll pendulum;the center of mass acceleration;conservation of mechanical energy;energy allocation
*浙江大学城市学院 2017年度大学生科研训练项目,项目编号:X2017522065
储若超(1995- ),男,在读本科生.
指导教师:张锐波(1959- ),男,副教授,研究方向:大学物理实验技术、创新设计与教学方法研究.
2017-03-30)
