碰撞问题的速度矩阵表达和能量损失及传递率分析*

贺西平 王成会 边小兵 卢红兵

(陕西师范大学物理学与信息技术学院 陕西 西安 710119)

碰撞问题的速度矩阵表达和能量损失及传递率分析*

贺西平 王成会 边小兵 卢红兵

(陕西师范大学物理学与信息技术学院 陕西 西安 710119)

以两体碰撞为例，对碰撞前后的速度关系利用矩阵作了简明表达．全面分析了碰撞前后的能量组成及关系，阐述了资用能的物理意义，求出了能量损失、能量传递率等表达式．本文的分析方法也可推广到多体碰撞问题中去．

能量损失 能量传递率 速度矩阵 多体碰撞

文献[1]在不引入惯性力的前提下，讨论了两体问题中的功能原理、机械能守恒定律的应用范围．文献[2～4]导出了两体对心碰撞的能量损失公式，指出了恢复系数实质为恢复阶段系统的动能增加值与压缩阶段中系统的动能减小值之比的平方根．利用柯尼希定理将两体碰撞前后的能量表达为质心动能与折合质量相对速度的动能(即资用能)之和，有助于理解资用能的物理意义[5]，也能够简化处理诸如子弹穿越木块、物块在凹槽里碰撞以及外部物体与两连接弹簧碰撞等问题[6]．碰撞的总能量，来源于碰撞前两体具有的动能，该动能除了碰撞后转化为其他形式而损失的能量外，还有碰后两体具有的动能．其中包含有一体传递给另一体的能量，由此可求出能量的传递率，有实用价值[7,8]．除了两体碰撞问题外，还会遇到诸如汽车连环追尾等多体碰撞的问题．

本文以两体碰撞为例，对碰撞前后的速度关系利用矩阵作了简明表达，全面分析了碰撞前后的能量组成、关系，并求出了能量损失、能量传递率表达式，由此可以更简便、更深刻地理解碰撞问题．本文的分析方法可推广到多体碰撞问题中去．

1 碰撞前后的速度矩阵表示

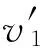
图1 两体碰撞前后的速度

由动量守恒定律，有

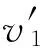
(1)

即u′=-eu

(2)

由以上两式，得到

碰撞前后速度之间的关系可用矩阵表达为

(3)

或者也可得到两体之间的碰前和碰后的关系

矩阵表达为

2 能量分析

碰撞前后该两体系统的动能E1和E2分别为

(4)

由此，两体系统能量损失ΔEk即为碰撞前后的资用能之差

(5)

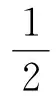
(6)

其中，E1f为质量m1碰撞后的动能，E2g为质量m2碰后得到的能量，Ed为碰撞过程中转换成其他形式的能量．

由式(3)可得

(7)

(8)

结合式(6)～(8)，碰撞过程中转换成其他形式的能量Ed为

Ed=E-E1f-E2g=

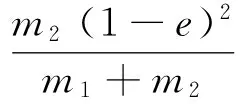
质量m1传递给m2的动能E2g与质量m1的动能之比，即能量的传递率η为

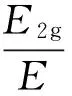
(9)

式中e为恢复系数，其值介于0与1之间．能量的传递率η与质量比t及恢复系数有关．为使得η达到最大，对上式进行如下讨论：

(1)若两球质量比t为恒定值，则e=1时，即完全弹性碰撞时，能量传递率达到最大，完全非弹性碰撞e=0时能量传递率最小；

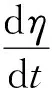
需要注意的是，碰撞过程中传递能量，或说是被碰撞质量获得的动能E2g与转换成其他形式的能量Ed是两个概念．

图2 三体碰撞前后的速度

根据式(3)，质量m2的碰前和碰后与质量m1的碰前和碰后速度之间的关系为

(10)

式中e1为m1和m2之间碰撞恢复系数．

同理，质量m3的碰前和碰后与质量m2的碰前和碰后速度之间的关系为

(11)

式中e2为m2和m3之间碰撞恢复系数．

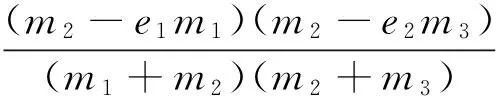
能量关系依上可进行类似的分析．

3 小结

本文以两体碰撞为例，全面分析了碰撞前后的能量组成及关系，利用矩阵对碰撞前后的速度关系作了简明表达．碰撞过程中转化为其他形式的能量与碰撞前后系统的资用能之差相等．若为完全非弹性碰撞，碰前的资用能将在碰撞过程中全部转化为其他形式的能量．

利用推导的碰撞前后的速度矩阵关系式，对碰撞过程中能量的传递率进行了分析，即碰撞球(物)体传递给被碰撞球(物)体的动能与碰前碰撞球(物)体所携带的动能之比．若两球质量比为恒定值，发生完全弹性碰撞时，能量传递率最大，完全非弹性碰撞时能量传递率最小．若恢复系数为恒定值，当两碰撞球体的质量相等时，动能的传递率为最大．

利用推导的碰撞前后的速度矩阵关系式，也容易分析多体碰撞问题中的能量关系以及碰撞物体从前到后的能量传递率．

1 白静江.两体问题中的功能原理及机械能守恒定律.大学物理,1997,16(3): 11～14

2 刘超.两体对心碰撞能量损失问题初探.物理教学探讨,2004,22(213):51～52

3 王长春.从能量的角度讨论两体碰撞问题.大学物理, 2005, 24(9):18～22

4 M F Ferreira da Silva.Meaning and usefulness of the coefficient of restitution. Eur J Phys, 2007, 28 (6):

1 219～1 232

5 陈钢,阮中中.柯尼希定理运用于两体问题的讨论.物理与工程, 2010,20(1):21～22,31

6 范继美.两体问题中的折合质量.昆明工学院学报,1992,17(2):121～128

7 Marián Kireš.Astroblaster-a fascinating game of multi-ball collisions.Phys Edu,2009,44 (2),159～164

8 BernardRicardo,Paul Lee.Maximizing kinetic energy transfer in one-dimensional many-body collisions,Eur J Phys,2015,36 (2):1～12

9 蔡支坤,王笑君.运用质心系解决两体碰撞问题.物理通报, 2016(2):8～10

AnalysisonVelocityMatrixRepresentation,EnergyLossandTransferRateofImpactIssue

He Xiping Wan Chenhui Bian Xiaobing Lu Hongbing

(Shaanxi Normal University,School of Physics Information Technology,Xi'an,Shaanxi 710119)

Taking the two-body collision as an example, the relation of bodies velocity between before and after collision is concisely expressed in matrix form. The component parts of collision energy of the bodies and their relations between before and after collision are analyzed thoroughly and the physical meaning of available energy is elaborated, furthermore, expressions of the loss of energy and the energy transfer rate are derived. The analysis method described here may be adopted for many-body collisions issues.

loss of energy; energy transfer rate; velocity matrix; many-body collisions

*陕西师范大学教学改革项目资助．

贺西平(1965- ),男,博士，教授，主要从事力学、理论力学教学和超声学研究工作.

2017-04-21)