原油价格波动对中国股票市场的风险溢出效应研究
2017-11-16
(湖南商学院,湖南 长沙 410205)
原油价格波动对中国股票市场的风险溢出效应研究
欧阳资生李钊
(湖南商学院,湖南长沙410205)
针对原油价格波动对中国股票市场是否存在溢出效应问题,首先利用POT模型构建布伦特原油价格和上证指数的边缘分布,然后采用Copula方法分析其相依结构,得到最合适的Copula函数,最后采用CoVaR方法对溢出效应进行测度。度量同时期原油价格波动对美国股票市场的风险溢出值作为对比,结果表明原油价格波动对中国股票市场的风险溢出效应相较于美国市场而言比较有限,并分析可能是由于我国长期以来一直实行的成品油定价机制的原因。
原油价格;Copula函数;溢出效应
一、引言
原油作为一种重要的战略性能源,对国家工业现代化的深入推进和国民经济的持续健康发展起着至关重要的作用。历史上每一次国际原油价格发生大幅的波动,均对世界各国的宏观经济产生了巨大的冲击。由于原油作为一种重要的大宗商品本身兼具一般商品和金融商品的属性,因此原油价格波动也会对各国的金融市场产生一定程度的风险传染,且对“国民经济晴雨表”——股票市场的风险传染尤为显著。从原油价格波动造成股票市场波动的机理分析,首先,原油价格的波动通常被视为燃料成本的波动,进而会直接影响上市企业的利润水平甚至于股票市场的股价表现,这种影响对于能源对外依存度高的国家更为明显[1];其次,原油价格的波动会显著影响石油出口国的财政收入,从而影响该国主权财富基金在全世界各主要股票市场的投资行为,导致各主要股票市场的波动[2];最后,作为最重要的大宗商品,原油价格的波动势必会加速国际资本的流动,并导致世界各主要的股票市场的波动[3]。当前,我国作为全球最大原油进口国和消费国,国内外投资者也都十分关注原油价格波动对中国A股市场的影响,因此,分析原油价格波动对中国股票市场的风险溢出效应具有重要的理论和现实意义。
事实上,学术界针对原油价格波动对股票市场的影响已经进行了诸多研究,但笔者注意到,原油价格波动如何影响中国股票市场风险传染途径,特别是原油价格波动对中国股票市场的风险溢出测度的研究很少,还需要进一步分析讨论。Arouri et al.[4]以海湾合作委员会成员国2005年至2010年数据为样本,基于VAR-GARCH方法分析石油-股票投资组合的最优权重和套期保值比率,发现成员国内国际油价与其股票市场存在着持续的波动溢出效应;Sadorsky[5]利用多元GARCH模型,研究分析了石油价格与清洁能源公司和科技公司股价的条件相关与波动率溢出效应;Chang et al.[6]利用CCC模型、VARMA-GARCH模型和DCC模型,研究分析了原油价格和股市指数之间的条件相关与波动率溢出效应;Lin et al.[7]利用VAR-GARCH模型、VAR-AGARCH模型和DCC-GARCH模型研究了石油价格和加纳股市的动态波动性和波动性传播;Khalfaoui et al.[8]基于小波变换的MGARCH模型,研究了不同时间跨度下WTI原油价格和G7国家的股票市场的均值与波动率溢出效应;Bouri[9]基于ARMAX-GARCH模型拟合收益率的条件均值和条件方差,研究了黎巴嫩和约旦等石油进口国家石油价格对股票市场的波动率溢出效应;Ewing和Malik[10]通过迭代算法测算结构突变,基于结构突变的基础上利用二元GARCH模型,发现石油价格和股票市场存在显著的波动溢出效应。
金洪飞等[11]利用VAR结合二元GARCH模型,分析了国际石油价格对中、美两国股票市场的收益率和波动的溢出效应;薛永刚[12]通过对布伦特原油价格和28个国家的股价指数进行研究,认为国际油价对不同国家股市的溢出影响存在差异性;闻岳春等[13]利用VAR和DCC-MGARCH模型,研究了中国股市和香港、日本、美国、欧洲等主要国际股票市场,与石油、铜、黄金为代表的三种国际大宗商品之间的收益率和波动率溢出情况;李素芳等[14]利用贝叶斯门限机制转换协整模型,实证分析了国际油价与八个亚太股票市场间的非线性动态关系;朱慧明等[15]利用Copula函数研究了WTI原油价格与金砖五国股市的关系,并认为国际原油价格和A股市场的相关关系比较弱,和其余四个国家的股市相关关系比较显著。
综合以上文献归纳与梳理不难发现,研究方法上,现有研究通常是结合VAR和多元GARCH模型测度原油价格和股票市场之间的溢出效应。然而上述两种方法并不能有效避免由于序列存在的尖峰厚尾的特性而影响测量的误差,且VAR方法只能定性地描述两个市场之间风险传导方向,无法有效测度风险溢出大小和刻画相依关系的强度;多元GARCH方法在刻画相依关系时通常需要假定变量都满足同分布,显然在实际操作中要求比较严苛。Copula函数不要求变量服从同分布假设,可以很好地刻画多个变量之间的非线性尾部相依结构。鉴于此,笔者采用Copula函数和EVT极值理论的方法开展实证研究。
二、Copula-EVT-CoVaR模型介绍
1.极值理论(EVT)模型构造边缘分布
极值理论(Extreme Value Theory)通常是用以刻画金融时间序列分布中存在的尖峰厚尾的特性,尖峰厚尾的分布特点表明极端事件的出现概率会比正态分布条件下大很多,正因如此,该方法更加关注极端风险状况。EVT模型按估计方法不同可以分为两种:其一是划分同等样本容量的分区块取最大值的BMM模型;其二是针对所有数据取某一个充分大的阈值,超过阈值之上观测值序列建立模型以刻画极端事件的POT模型,POT模型是近年来刻画极端风险的常用方法,后面的建模中也选用这种方法。
POT模型只针对超过阈值的观测值时间序列构建模型,其分布的定义表示为:
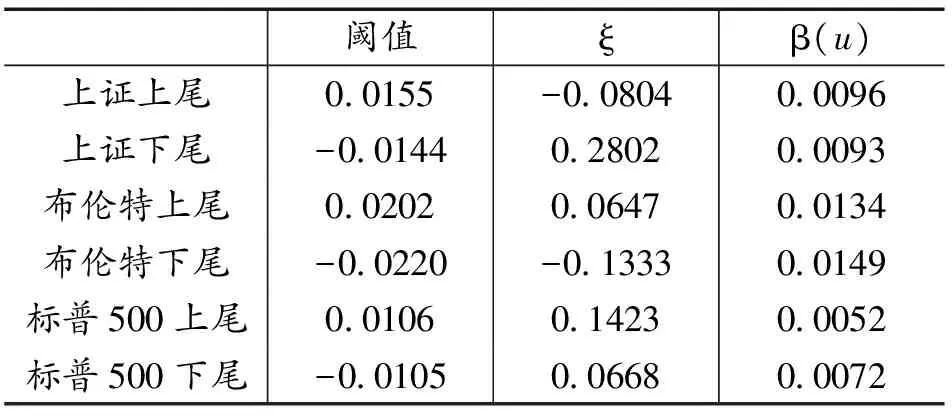
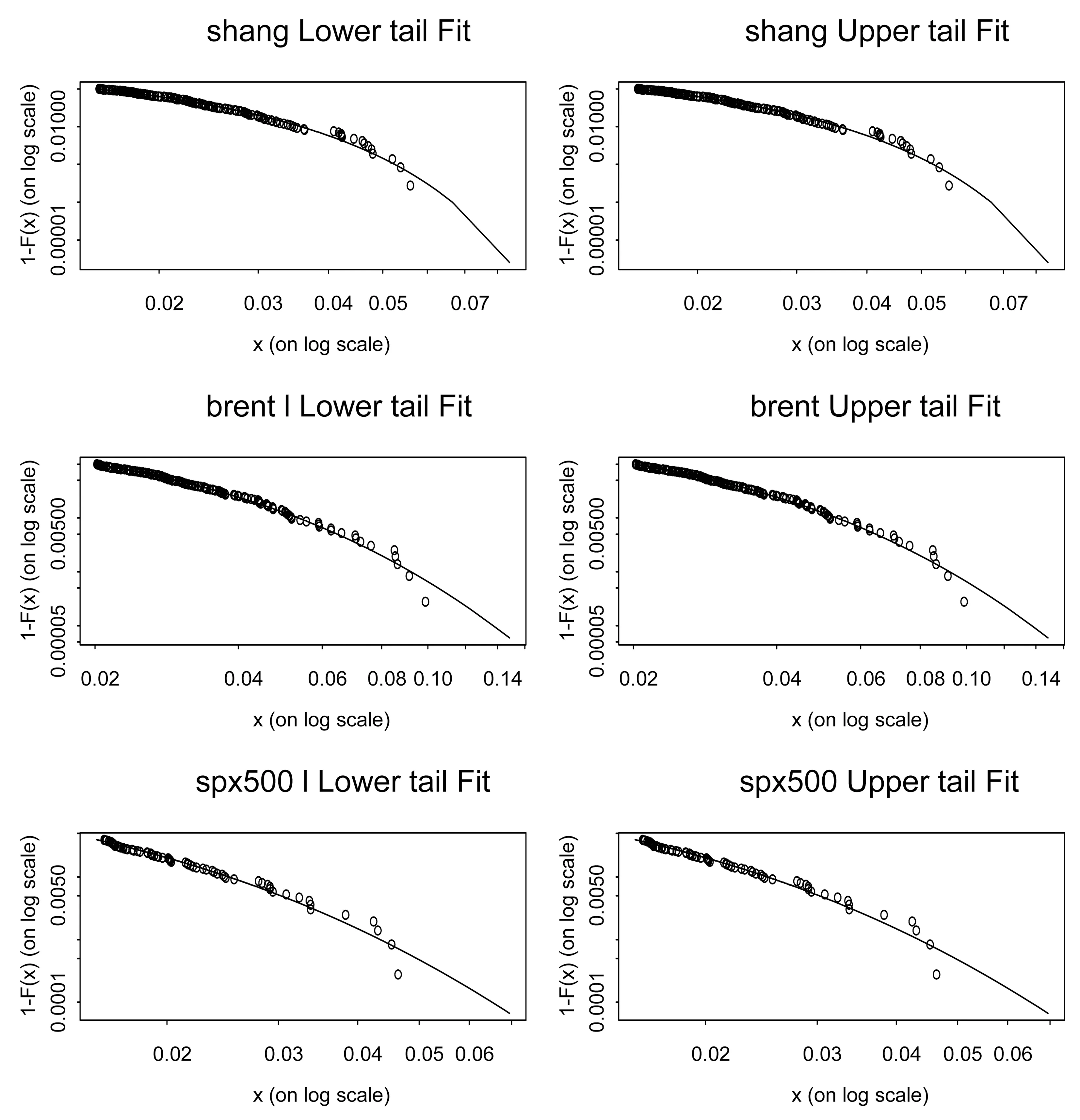
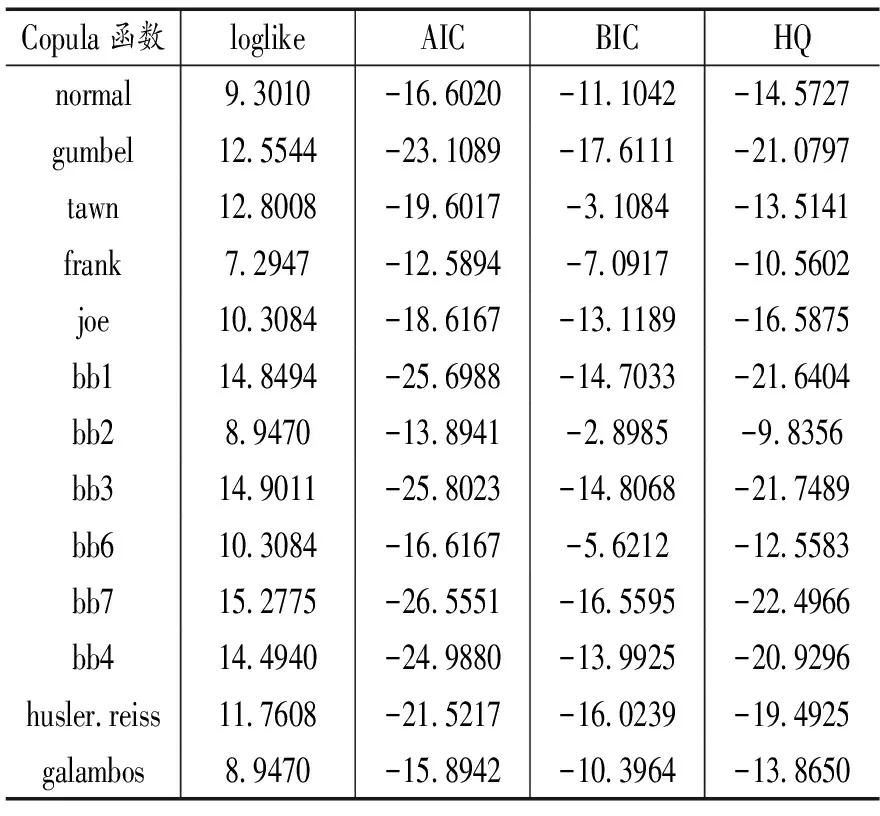
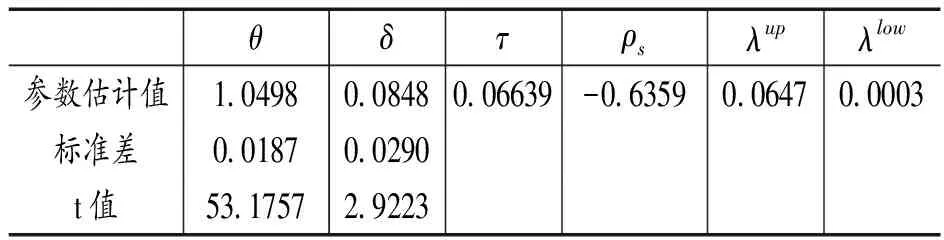
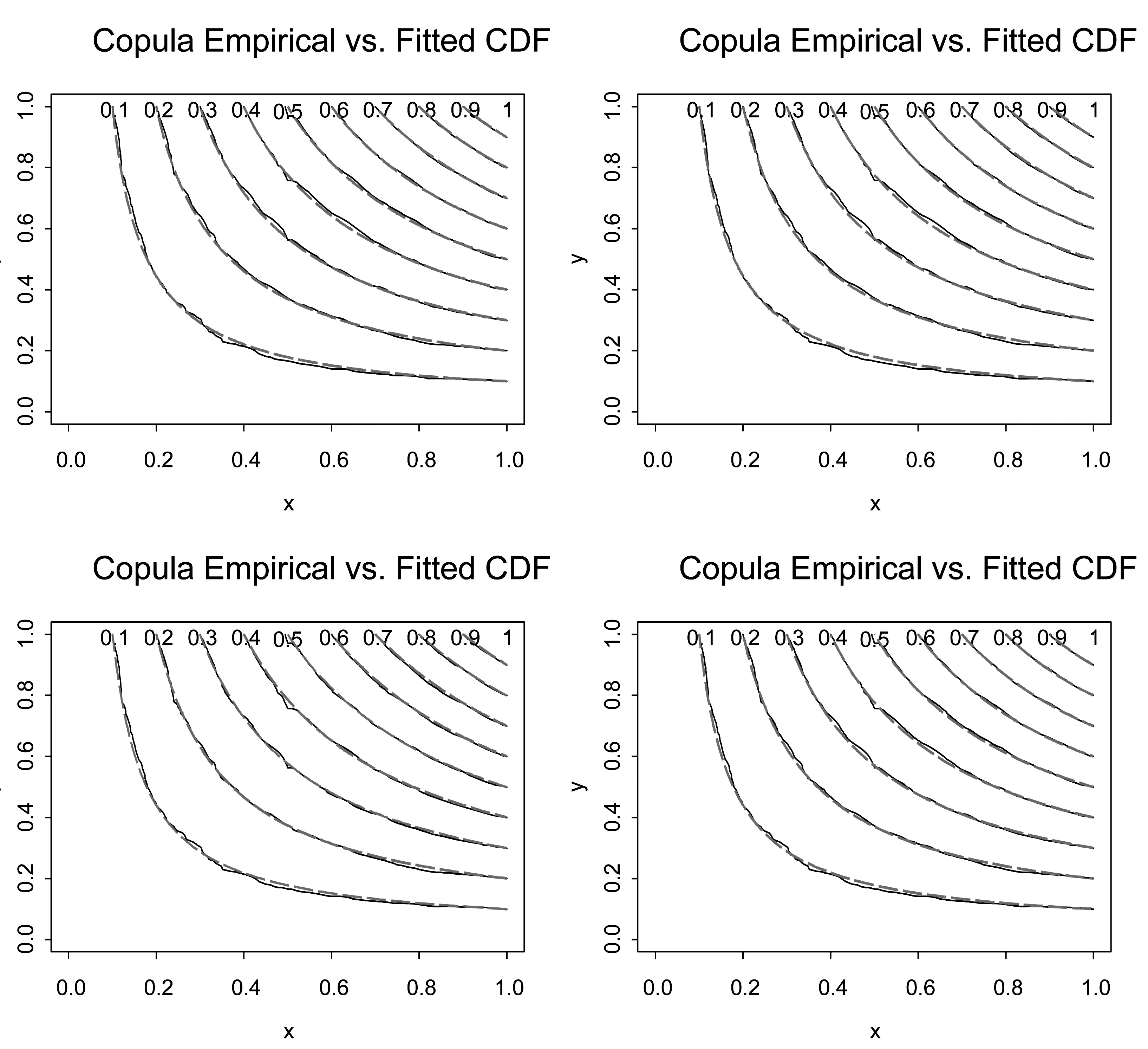
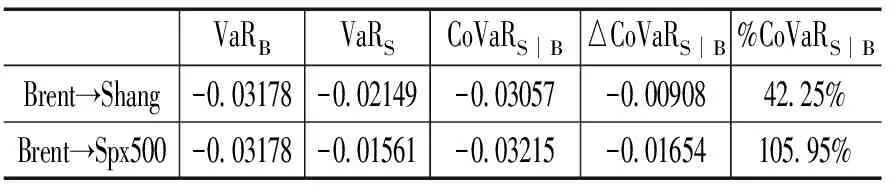
Fu(y)=Pr(X-uy|X>u)=,0 (1) xF为分布F的右端点。当u充分大时,分布函数Fu(y)会收敛于GPD模型Gξ,β(y),其表达式可写为: (2) 式中,ξ和β分别为形状参数和尺度参数。当ξ≥0时,y≥0,此时F是Frechet分布,Gξ,β(y)是Pareto分布;当ξ<0时,0y-,此时F是Weibull分布,Gξ,β(y)是ParetoⅡ分布;当ξ=0,F是Gumbel分布,Gξ,β(y)是指数分布。对参数ξ,β的估计,由于β取决与阈值u的大小,当前确定u的方法有均值超额图法、Hill图法、峰度法和样本10%原则,前三种方法有比较大的主观性,所以笔者采取第四种方法,即将u确定为使得超过u的观测值个数占样本容量的10%。 对于形状参数ξ、尺度参数β(u)的估计,通常采用MLE方法。其中GPD分的对数似然函数为: l(ξ,β(u))= (3) 2.Copula模型与相关性度量 Copula函数实际上可以被看成是一个连接函数,一个将多元随机变量的联合分布函数和每个变量各自的边缘分布函数相互连接起来的函数。Copula函数是由Sklar于1996年首次提出的,用以度量变量之间的相依结构,Sklar定理指出:假设F为一个N维的联合分布函数,其各自的边缘为F1,F2,…,Fn-1,Fn,则存在一个N维的Copula函数C(·,·,…,·)满足: F(x1,x2,…,xn)=Pr(X1≤x1,X2≤x2,…,Xn≤xn) =Pr(FX1(X1)≤FX1(x1),FX2(X2)≤FX2(x2),…,FXn(Xn)≤FXn(xn)) =C(FX1(x1),FX2(x2),…,FXn(xn))=C(·,·,…,·) (4) 假如FX1(x1),FX2(x2),…,FXn(xn)是连续函数,则C(·,·,…,·)是唯一的。 Pearson相关系数、Spearman’s rho相关系数、Kendall’s tau相关系数与尾部相关系数是风险管理当中比较常见的几种度量相关性的参数。其中,Pearson相关系数ρ常用来度线性相关关系,并且要求随机变量的方差是有限的,然而金融时间序列一般都呈现出尖峰厚尾,方差也并不总是存在;Spearman相关系数ρs通常用来度量变量之间的相关性可以用单调函数进行刻画,可以度量非线性关系;Kendall’s tau相关系数τ是一种以样本的顺序统计量为基础的非参数方法,同样也可以度量非线性关系;尾部相关系数分为上尾相关系数λup和下尾相关系数λlow,主要用以度量尾部相依结构。各相关系数表达式依次为: (5) (6) (7) (8) (9) 3.CoVaR的度量 (1)VaR的度量 VaR(Value at risk)在险价值指的是在一定的置信度水平下,金融资产在未来某一个特定期间里最坏情况下的损失大小。该指标简单清晰地刻画了在未来某一个特定期间里收益与损失的预期分布的分位数,如果金融资产在t时刻的收益率为rt,则分位数(1-α)下的在险价值VaR可以定义为: Pr(rt≤VaRα,t)=α (10) 定义表示金融资产未来某个期间里在(1-α)的置信度下,损失最大不超过VaRα,t。 对于VaR的估计,如果金融资产的损失为时间序列X,其损失分布函数为F(x),则VaR可表示为: VaRα=inf{x|F(X≤x)>α} (11) 当F(x) 是连续函数,就会有VaRα=F-1(α) ,其中F-1为F反函数。 (2)CoVaR的度量 (12) (13) (14) 对于CoVaR的估计,参考Girardi and Ergün[17]的思路,假设收益率时间序列Xi和Xj的联合概率密度以及各自的边缘概率密度分别为f(xi,xj),fi(xi),fj(xj),则结合Copula函数有Xi的条件概率密度函数为: =c(Fi(xi),Fj(xj))fi(xi)(15) 则有: (16) (17) 1.数据处理与描述 对于中国股票市场,选用上证综合指数刻画中国市场股价的波动情况;对于美国股票市场,由于标准普尔500指数相比道琼斯指数而言,其风险更分散,可以代表更广泛的美国股市的市场变化,因此以其代表美股;对于国际原油价格,选取国际上广泛使用的布伦特原油期货价格作为样本,三组数据的起止期间均为2010年1月4日至2017年8月31日(两组股指数据都来源于同花顺数据库,布伦特原油期指来源于美国能源信息署)。对三组时间序列剔除节假日和不在同一个交易日的数据后,剩下1804个有效数据。将三组数据换算成收益率形式,其公式为: rt=ln(Pt/Pt-1) (18) 将上证指数、布伦特原油期货价格与标准普尔500指数收益率进行描述性统计,计算结果如表1所示。 表1 三组收益率序列的收益率描述性统计量 注:LM(10)为滞后10阶的检验统计量,括号内是各统计量的P值 根据表1可知,上证指数和布伦特原油指数的收益率时间序列的ADF值均明显小于各显著性水平下的临界值,显然均是平稳序列。三组收益率序列的偏度都为负数,呈现左偏分布;三者的峰度值均大于3,且三者J-B统计量的P值都为0,明显收益率序列具有非正态性,显而易见,三组收益率序列均服从尖峰厚尾分布,可以考虑用EVT模型刻画其收益率分布形式。 2.EVT模型构造边缘分布及其参数估计 采用极值理论(EVT)中的GP分布拟合三组收益率序列的上尾和下尾结构。首先,关于阈值的选取,根据Dumouchel[18]和周孝华等[19]等提出的10%原则确定上尾和下尾的阈值,即将确定为使得超过的观测值个数占样本容量的。采取最大似然估计(MLE)的方法对上尾和下尾分布的形状参数、尺度参数进行估计,估计结果见表2,拟合效果见图1。 表2 三组收益率序列的GPD模型上尾和下尾参数估计 依据表2的结果,再做出三组收益率序列的GPD模型拟合效果图(如图1所示),可知三组收益率序列的上尾部分和下尾部分除了少数几个点外,绝大多数点都落在拟合的曲线上,显然,采用GPD模型用以刻画三组收益率序列的尖峰厚尾特性的拟合效果比较理想。 图1三组收益率序列的GPD模型上尾和下尾拟合效果 3.Copula函数的构建与参数估计 在对三组收益率序列的上尾和下尾结构进行GPD模型拟合的基础上,进一步利用Copula函数的方法分析布伦特原油期货价格收益率和上证指数收益率、布伦特原油期货价格收益率和标准普尔500指数收益率,利用各自边缘分布拟合结果进行下一阶段相依结构关系的刻画。笔者选取了normal Copula、gumbel Copula、tawn Copula、husler.reiss Copula、galambos Copula等各种Copula函数作为目标Copula函数的可选项,并将这些Copula函数的计算结果进行对比以选择最优Copula函数。考虑到篇幅,仅列出布伦特收益率和上证指数收益率相依结构的Copula函数计算结果,各Copula函数簇拟合结果的参数估计和效果对比见表3。 显然,根据AIC、BIC、HQ值最小原则和loglike值最大原则,bb7 Copula函数是所有函数中拟合效果最好的。布伦特收益率和上证指数收益率相依结构的bb7 Copula函数的参数与相关系数估计结果见表4。由表4可知,除了Spearman系数较大以外,其余三个相关系数都比较小,可见两个市场的非线性相关性不是非常明显。 表3 Copula函数簇拟合结果的参数估计和效果对比(布伦特和上证指数) 表4 bb7 Copula函数的参数与相关系数估计 为进一步直观体现bb7 Copula是上述Copula函数中最理想的,作图2,将normal Copula(上左)、frank Copula(上右)、bb2 Copula(下左)和bb7 Copula(下右)的拟合图进行对比。显然,总体而言,bb7 Copula函数拟合效果要优于其他三类 Copula函数簇的拟合效果。 图2 normal Copula(上左)、frank Copula(上右)、bb2 Copula(下左)和bb7 Copula(下右)的拟合对比图(布伦特和上证指数) 4.溢出效应的CoVaR度量 结合式(11)-(17),计算得出在置信水平时上证指数的在险价值VaRS,布伦特原油在险价值VaRB,当布伦特原油在险价值为VaRB时的上证指数条件在险价值CoVaRS∣B以及相应的△CoVaRS∣B,%CoVaRS∣B,同理也可计算出美国股票市场的相关值,具体计算结果见表5。显然依据公式(14)计算得出布伦特原油对上证指数的风险溢出百分值%CoVaRS∣B仅为42.25%,而在同时期,原油价格波动对标普500的风险溢出百分值%CoVaRS∣B为105.95%。相比较可知,相对于美国股票市场,国际原油价格的波动对中国的上证指数股价波动的风险溢出效应比较有限。 表5 布伦特原油价格波动对上证指数的溢出度量结果 首先利用POT模型很好地拟合与刻画了三组收益率时间序列的尖峰厚尾性;然后,采用Copula函数方法对国际油价和上证指数之间的相依结构进行刻画,根据AIC和BIC最小的原则,发现Copula函数簇中的BB7 Copula对其相依结构的刻画效果非常理想,同时似然值也是最大的;最后,采用CoVaR方法对溢出效应进行度量,结果表明 %CoVaRS∣B仅为42.25%,而同时期,美国股票市场的%CoVaRS∣B值为105.95%,相比较之下可知,国际原油价格对中国股票市场的风险溢出效应是比较有限的。 通常,原油作为经济发展的重要生产资料,原油价格的上涨通过下游产业链条的成本传导,既会通过最终产品使得CPI攀升进而影响民生,也会通过中间产品使得企业生产成本提高影响企业层面的盈利能力,对上市公司的股价产生影响。当前国际原油价格的波动对我国股票市场的风险溢出效应,相对于美国市场而言比较有限,可能的原因是由于我国长期以来一直在执行的行政干预性强的成品油定价机制的存在,该机制大幅度缓解了国际原油价格波动对我国宏观经济的消极影响,使得我国成品油价与国际原油价格接轨程度比较小,同时也使得市场机制无法有效地优化资源配置[20][21][22]。 [1]Bernanke B S.The relationship between stocks and oil prices[R].Washington,DC: Brookings Institution,2016:1-6. [2]Arezki R,Mazarei A,Prasad A.Sovereign wealth funds in the new era of oil[R].Washington,DC:IMF Blog,2015:1-6. [3]Nandha,M.,& Faff, R. Does oil move equity prices? a global view[J]. Energy Economics,2008(3):986-997. [4] Arouri,M.E.H.,Lahiani,A.,& Nguyen,D. K. Return and volatility transmission between world oil prices and stock markets of the gcc countries[J]. Economic Modelling,2011(4):1815-1825. [5]Sadorsky,P. Correlations and volatility spillovers between oil prices and the stock prices of clean energy and technology companies[J]. Energy Economics,2012(1):248-255. [6]Chang,C. L.,Mcaleer,M.,& Tansuchat, R. Conditional Correlations and Volatility Spillovers Between Crude Oil and Stock Index Returns[J]. North American Journal of Economics and Finance,2013(25):116-138. [7]Lin,B.,Jr,P. K. W.,& Appiah,M. O. Oil price fluctuation,volatility spillover and the ghanaian equity market:implication for portfolio management and hedging effectiveness[J]. Energy Economics,2014(1):172-182. [8] Khalfaoui,R.,Boutahar,M.,&Boubaker,H. Analyzing volatility spillovers and hedging between oil and stock markets: evidence from wavelet analysis[J].Energy Economics,2015(49):540-549. [9]Bouri,E. Oil volatility shocks and the stock markets of oil-importing mena economies: a tale from the financial crisis[J]. Energy Economics,2015(51):590-598 [10] Ewing,B. T.,& Malik, F. Volatility spillovers between oil prices and the stock market under structural breaks[J]. Global Finance Journal,2016(29):12-23. [11]金洪飞,金 荦.石油价格与股票市场的溢出效应——基于中美数据的比较分析[J].金融研究,2008(2):83-97. [12]薛永刚. 国际石油价格波动的股票市场溢出效应研究——来自28个国家和地区样本数据的经验分析[J].中央财经大学学报,2011(9):30-36. [13]闻岳春,王 婕,程天笑. 国内股市与国际股市、大宗商品市场的溢出效应研究[J]. 国际金融研究,2015(8):31-43. [14]李素芳,朱慧明,李 荣. 基于贝叶斯机制转换协整模型的石油——股市非对称效应研究[J]. 中国管理科学,2015(9):46-54. [15]朱慧明,董 丹,郭 鹏.基于Copula函数的国际原油价格与股票市场收益的相关性研究[J].财经理论与实践,2016(2):32-37. [16]Adrian T, Brunnermeier M K. CoVaR. Princeton University[C].Working Paper,2008:1-27. [17]Girardi,G.,& Ergün,A.T.Systemic risk measurement:multivariate garch estimation of covar[J]. Journal of Banking & Finance,2013(8):3169-3180. [18]Dumouchel, W. H. Estimating the stable index α in order to measure tail thickness:acritique[J]. Annals of Statistics,1983(4):1019-1031. [19]周孝华,陈九生.基于Copula-ASV-EVT-CoVaR模型的中小板与创业板风险溢出度量研究[J].系统工程理论与实践,2016(3):559-568. [20]Bouri,E.,Chen,Q.,Lien,D.,&Lv,X. Causality between oil prices and the stock market in china:the relevance of the reformed oil product pricing mechanism[J]. International Review of Economics & Finance,2017(48):34-48. [21]Chen,Q.,& Lv,X.The extreme-value dependence between the crude oil price and chinese stock markets[J]. International Review of Economics & Finance, 2015(39):121-132. [22]胡光辉,孟艳莉,张玉柯.国际石油价格波动对中国外贸的影响:理论综述与实证分析[J].贵州财经大学学报,2013(3):104-110. StudyonRiskSpilloverEffectofCrudeOilPriceFluctuationonChineseStockMarket OUYANG Zi-sheng Li Zhao In order to verify whether the oil price fluctuation has risk spillover effect on Chinese stock market, we have taken Brent oil price , China's Shanghai Composite Index and S&P 500 as the research object, adopted POT (peak over threshold) model to fit the marginal distribution of Brent oil price and China's Shanghai Composite Index,constructed Copula method to capture the risk-dependent structure between them and employed CoVaR approach to measure the risk spillover value. Meanwhile, we also take the same type of step to measure the risk spillover value of Brent oil price on S&P 500. According to these two risk Spillover values, and find that the risk spillover effect of crude oil price fluctuation on Chinese stock market is rather limited compared to the American market which may be due to the existence of refined oil pricing mechanism in China. crude oil price; opula function; spillover effect 10.16546/j.cnki.cn43-1510/f.2017.05.004 F416.22;F832.51 A 2095-1361(2017)05-0038-08 2017-09-02 国家社会科学基金重点项目“网络舆情影响下的金融系统性风险度量与预警研究”(项目编号:17ATJ005) 欧阳资生(1967- ),男,湖南邵阳人,湖南商学院教授,博士,硕士研究生导师,教育部金融学类教学指导委员会委员,研究方向:金融风险管理 (编辑:余华;校对:周亮)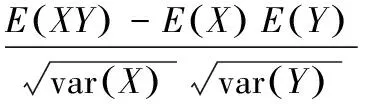
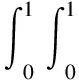
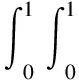
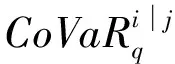
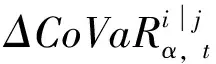
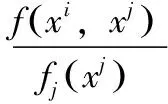
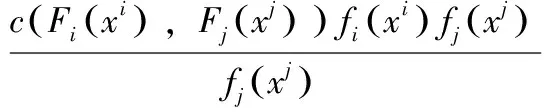
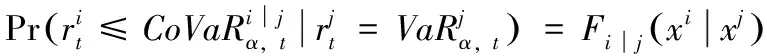

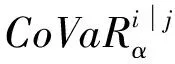
三、原油价格对中国股市溢出效应的实证分析

四、结论
(HunanUniversityofCommerce,ChangshaHunan410205)
