三相电压型PWM整流器控制策略的优化研究

冯 菁,熊 璐,李文转

(1.华中光电技术研究所 武汉光电国家实验室，武汉 430223；2.华中科技大学 电气与电子工程学院，武汉 430074)

三相电压型PWM整流器控制策略的优化研究

冯 菁1,熊 璐1,李文转2

(1.华中光电技术研究所 武汉光电国家实验室，武汉 430223；2.华中科技大学 电气与电子工程学院，武汉 430074)

三相电压型高频PWM整流器的控制策略是一种基于d-q坐标系下的电流、电压双闭环控制。为了研究传统三相电压型PWM整流器控制效果与交流侧电感参数的关系，借鉴合成矢量的方法，通过分析三相电压型PWM整流器的数学模型和控制策略，提出了一种在d-q坐标系下，电压、电流双闭环，无需使用电感参数的电流解耦控制方案。MATLAB仿真结果表明，使用改进的控制策略，系统结构简单，响应速度快，鲁棒性好，容易实现，有效解决了电感参数变化带来的问题。

PWM整流；无电感值解耦；双闭环控制；MATLAB仿真

三相电压型PWM整流器是一种高效、可靠、绿色的电能变换装置。单位功率因数的电压型PWM整流器由于具有网侧电流谐波含量少、电能可双向传输、动态响应快等优点[1]，从而被广泛的应用。 三相电压型PWM整流器通常采用直流电压、交流电流双闭环控制方式，外环控制给内环控制提供指令。根据内环控制方法的不同，三相电压型PWM整流器的控制策略可主要分为[2]：内环采用电流控制[3](电压、电流双闭环控制);内环采用功率控制[4](直接功率控制DPC)；内环采用时间最优控制[5]。对于PWM整流器主电路的设计方法，在国内外文献中主要是针对电流控制策略、SPWM调制方式的，基于电流解耦的系统控制器设计不适于整流器DPC系统设计，文献[6]按照DPC的特点设计了一个基于电路主要参数的新方法。文献[7]在直接转矩控制的基础上引入空间矢量调制以及虚拟磁链的思想来解决直接转矩控制中开关频率不固定带来的一系列问题。文献[8]提出的空间矢量控制和预测控制的策略大体上消除了开关频率持续变化的问题，使三相电压型PWM整流器的性能显著提高。目前基于同步旋转d-q坐标系下的双闭环控制是被人们广泛实际使用的方法。这种控制方法易于实现，缺点是在其电流分量解耦的过程中必须使用精确的交流侧电感值[9-11]。本文对基于同步旋转d-q坐标系的电压、电流双闭环控制进行改进，通过合成矢量的方法，提出了一种在同步旋转d-q坐标系下无需知道准确交流电感L参数的电流内环解耦控制方法。最后通过MATLAB仿真对比验证验证了所提控制方案的正确性和有效性。

1 三相电压型PWM整流器的数学模型

三相电压型PWM整流器的拓扑结构如图1所示。

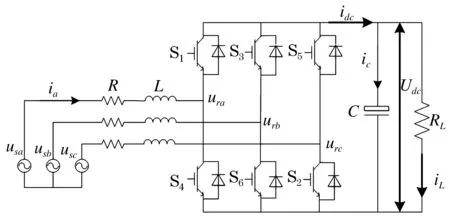
usa、usb、usc—交流侧三相电压；ia—交流侧三相电流；udc—直流侧输出电压；iL—负载电流。R—开关管的开关损耗等效电阻加上交流侧电感的电阻；L—交流侧电感；C—直流侧电容；RL—负载阻抗。

图1三相电压型PWM整流器的拓扑结构

Fig.1Topologicalstructureofthree-phasevoltage-sourcedPWMrectifier

为了分析图1，开始先定义单极性零一开关函数sk为

(1)

其中：k=a、b、c。

假设三相交流电压对称，三相交流线路电阻电感对称，可以建立三相电压型PWM整流器在三相静止坐标系下的数学模型为

(2)

三相静止坐标系下的数学模型具有各变量直观，明确等特点。然而由于变换器交流侧的变量都是瞬时变化的交流量，这对于设计控制系统来说非常复杂。

针对静止所标系下数学模型的缺点，可以借鉴电机控制中的矢量控制的观点对其进行改善，即将三相正弦量变为直流量。通过坐标旋转变换得到基于同步旋转d-q坐标系下的数学模型为

(3)

通过式(3) 能够实现对交流侧三相电流的无静差控制，可以建立三相电压型PWM整流器的数学模型，如图2所示。

图2 三相电压型PWM整流器的数学模型

2 控制策略

2.1 电流内环控制策略

近年来，随着高性能的数字信号处理芯片(DSP)的快速发展，已经可以实现现代控制理论中的一些复杂算法，达到了不错的控制效果。在三相整流器的控制系统设计方案中，通常采用电压外环和电流内环的双闭环控制。电压外环用来控制三相整流器的直流侧电压，电流内环是用来将电压外环输出的电流给定实行电流控制。

根据式(2)和PI调节器的控制思想，可将电流内环设计为

(4)

由式(4)可以得到同步旋转d-q坐标系下的电流解耦控制框图，如图3所示。在同步旋转d-q坐标系下，dq轴电流均为直流量，即可通过传统PI调节达到无静差跟踪。

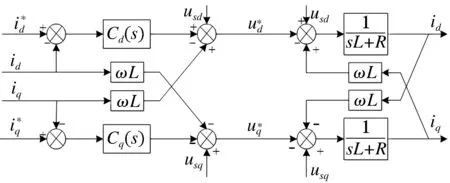
图3 同步旋转d-q坐标系下的电流解耦控制框图

在图3中：

(5)

同步旋转d-q坐标系下的电流解耦需要知道交流侧电感L的准确值。在实际运行和设计过程中，由于电感值会受到线路中的电流大小、环境变化的影响，因此在实际使用上往往会将解耦项省略。然而整流器开关频率不断提高，d-q轴间互相耦合的程度越来越大，这时耦合项将不能忽略，否则会恶化整流器控制性能。针对这个问题，有人借鉴合成矢量的控制思想，提出了无需精确电感L值的解耦控制。这种控制虽然解决了上述问题，但是需要纯矢量控制器，使用纯矢量控制器又有许多的困难和不便。基于这个原理，本文提出了一种基于同步旋转d-q坐标系，无需使用准确交流侧电感L值的电流内环解耦控制方案。

三相电压型PWM整流器在两相静止坐标系下的数学模型为

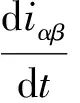
(6)

在用同步旋转坐标系下，微分算子d/dt+jω替换静止坐标系下的微分算子d/dt，就能得到同步旋转d-q坐标系下按照合成矢量原理的数学模型：

(7)

进一步简化：

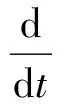
(8)

转换到s域：

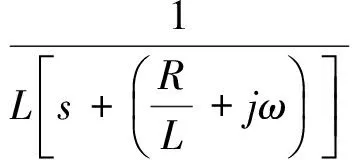
(9)

将R+jωL看作一个整体，设计PI调节器：

(10)

对此PI参数的整定同样可以使用传统的选定方法，也就是通过零极点对消原则和采用适当的截止频率来整定。同样可得到基于合成矢量的电流解耦控制框图，如图4所示。

图4 基于合成矢量的电流解耦控制

综上简化可得，本文控制方法中的电流内环设计为

(11)

图5 同步旋转d-q坐标系下的无电感L参数解耦控制框图

2.2 电压外环

电压外环控制主要是控制直流侧电压，维持直流电压恒定。从式(3)看出直流母线电压udc和d轴、q轴的电流相关，但是因为电流闭环的影响，动态过程中实际的iq的跳变非常小，而且在通常的双闭环控制系统中，外环的响应速度通常都低于内环，直流电压开始较大跳变之前，内环iq早已完成其暂态过程达到零值，因此可以暂时将q轴电流的影响忽略。

考虑到三相电压型PWM整流器常常工作在单位功率因素下，q轴的给定值为0，可以建立如图6所示的控制框图，图中虚线所示为本文改进控制策略部分。

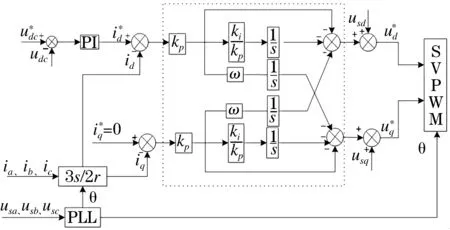
图6 总体控制框图

3 仿真分析

为了充分验证本文提出的无需电感L参数的电流内环解耦控制策略的正确性和实用性。本文基于此控制策略原理，用软件构建了仿真平台。仿真使用的三相电压型PWM整流器的各项参数如表1所示。

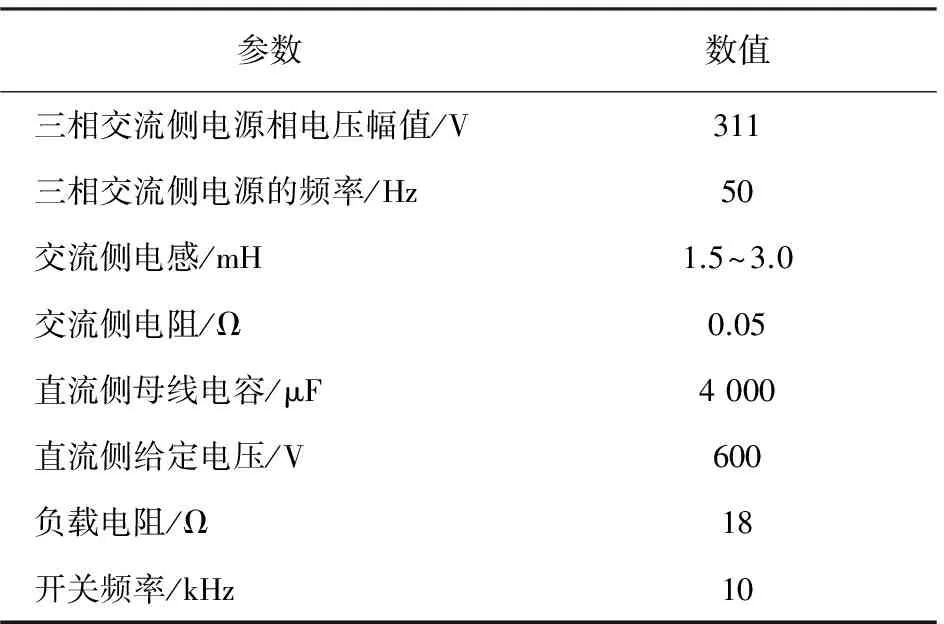
表1 三相电压型PWM整流的仿真参数

传统电压、电流双闭环控制时的交流侧电流和直流侧电压仿真波形如图7所示。当交流侧电感在0.2 s处由3mH突变为1.5 mH时，电流波形的总谐波畸变率THD由1.49%变为3.54%。改进控制方法下的交流侧电流和直流侧电压仿真波形如图8所示。当交流侧电感在0.2 s处由3 mH突变为1.5 mH时，电流波形的总谐波畸变率THD由1.15%变为2.01%。

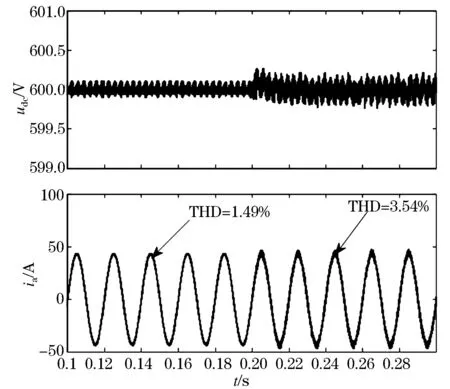
图 7 基于传统的双闭环控制策略的电压、电流波形

图8 基于改进的双闭环控制策略的电压、电流波形

比较图7和图8，当交流侧电感值不变的情况下，采用改进后的电压、电流双闭环控制时交流侧电流的总谐波畸变率要比传统双闭环控制下的要小；在电感突变时，采用改进后的控制方法下的直流侧电压变化比传统控制方法下的直流侧电压变化明显小；在交流侧电感突变时，采用改进后的控制方法下的交流侧电流总谐波畸变率变化比传统控制方法时小的多，这个减小量比较小，一般可视为交流侧电流几乎没有变化。从而验证了无电感L参数的电感解耦内环的正确性和可行性。

图9 基于传统双闭环控制策略在负载突变时的电压、电流波形

图10 基于改进双闭环控制策略在负载突变时的电压、电流波形

基于传统电压电流双闭环控制策略的三相VSR在负载由18 Ω突变为12 Ω时的电压电流波形如图9所示。从图9可以看出，系统启动后40 ms，直流母线电压达到稳定值。当负载在0.1 s处由18 Ω突变为12 Ω时，母线电压下降0.7%，系统经过20 ms后，再次达到稳定值600 V，负载电流有33 A突变为50 A。

基于改进的电压电流双闭环控制策略的三相VSR在负载由18 Ω突变为12 Ω时的电压电流波形如图10所示。从图10可以看出，系统启动后20 ms，直流母线电压达到稳定值。当负载在0.1 s处由18 Ω突变为12 Ω时，母线电压下降0.3%，系统经过15 ms后，再次达到稳定值600 V，负载电流有33 A突变为50 A。负载突变时网侧电流经过短暂的突变后，进入正常的运行中。

通过以上对比分析可知，新型控制策略的外环控制提高了系统的动态响应速度，并且改善了系统的负载抗扰动能力。综合分析三相VSR，使用新型电压电流双闭环策略能够实现电压超调小、响应快、稳定后交流侧电压电流同相位。

4 结 语

本文详细论述了三相电压型PWM整流器的数学模型，在传统双闭环控制方法的基础上，提出了一种在同步旋转d-q坐标系下，无需交流侧电感L精确值的电流内环解耦控制策略。仿真结果表明这种控制策略结构简单，响应速度快，电流畸变小，鲁棒性好，容易实现。

[1] 汪万伟，尹华杰，管霖．双闭环矢量控制的电压型PWM整流器参数整定[J]．电工技术学报，2010，25(2)：67-72．

WANG Wanwei，YIN Huajie，Guan Lin. Parameter setting for double closed-loop vector control of voltage source PWM rectifier[J]. Transactions of China Electrotechnical Society, 2010, 25(2): 67-72.

[2] 程启明，程尹曼，薛阳．三相电压型PWM整流器控制方法的发展综述[J]．电力系统保护与控制，2012，40(3)：145-155．

CHENG Qiming, CHENG Yinman, XUE Yang. A summary of current control methods for three-phase voltage-source PWM rectifiers[J]. Power System Protection and Control. 2012, 40(3): 145-155.

[3] Malesni L，Tenti P．A novel hysteresis control method for current controlled voltage-source PWM inverter with constant modulation frequency[J]．IEEE Transaction on industrial Applications．1990，26(1)：88-92.

[4] Malinowski M，Kazmierkowski M，Blaabjerg P K，et al．Virtual-flux-based direct power control of three-phase PWM rectifiers[J]．IEEE Transaction on industrial Applications．2001，37(4)：1019-1027．

[5] Jongwoo C，Seungki S．New current control concept-minimum current control in the three-phase PWM converter[J]．IEEE Transaction on Power Electronics．1997，12(1)：124-131．

[6] 王久和，李华德，王立明．电压型PWM整流器直接功率控制系统[J]．中国电机工程学报，2006，26(18)：54-60．WANG Jiuhe，LI Huade，WANG Liming．Direct power control system of three phase boost type PWMrectifiers[J]．Proceeding of the CSEE．2006，26(18)：54-60(in Chinese)．

[7] Malinowski M，Kazmierkowski M，Blaabjerg P K，et al．Virtual-flux-based direct power control of three-phase PWM rectifiers[J]．IEEE Transaction on industrial Applications．2001，37(4)：1019-1027．

[8] Bouafia A，Gaubert J P，Krim F．Predictive direct power control of three-phase pulsewidth modulation (PWM) rectifier using space-vector modulation(SVM)[J]．IEEE Transactions on Power Electronics，2010，25(1)：228-236．

[9] Yin B，Oruganti R，Panda S K，et al．A simple single-input-single-output(SISO)model for a three-phase PWM rectifiers[J]．IEEE Transaction on Power Electronics．2009，24(3)：620-631．

[10] Briz F，Degner M W，Lorenz R D．Analysis and design of current regulation using complex vectors[J]．IEEE Transaction on industrial Applications．2000，36(3)：815-825．

[11] 陈耀军，钟炎平．基于合成矢量的电压型PWM整流器电流控制研究[J]．中国电机工程学报，2006，26(2)：143-148．

CHEN Yaojun，ZHONG Yanping．Study on the current control for voltage-source PWM rectifier using complex vector[J]．Proceedings of the CSEE，2006，26(2)：52-56(in Chinese)．

Improvementon control strategyof three-phase voltage-sourced PWM rectifier

FENG Jing1,XIONG Lu1,LI Wenzhuan2

(1. National Laboratory for Optoelectronics,Huazhong Institute of Electro-optics,Wuhan 430223,China; 2. School of Electrical and Electronic Engineering,Huazhong University of Science and Technology,Wuhan 430074,China)

The control strategy of three-phase voltage-sourced high frequency PWM rectifier is based on current and voltage double closed-loop controlunder the d-q coordinate system. In order to study the relationship between the control effect of the traditional three-phase voltage-type PWM rectifier and the AC-side inductance parameter, the method of synthesizing vector. is used and thena mathematical model and a control strategy of the three-phase voltage-sourcedPWM rectifieris analyzed, in order topropose the current decoupling control programwithout the use of inductance parameters underd-qcoordinate systemand with voltage andcurrent double-closed loop. MATLAB simulation results show that the improved control strategyis ofsimple system structure, offast response, of good robustness, and easy to implement, which effectively solves the problem caused by changes in inductance parameters.

PWM rectification; decoupling withoutinductance; double closed-loop control; MATLAB simulation

2017-05-24；

2017-08-30。

冯 菁(1971—)，女，工程师，研究方向为应用电子技术。

TM461

A

2095-6843(2017)05-0382-05

(编辑侯世春)