具有截断控制参数学习效应及退化效应加工时间依赖于资源的单机排序问题

翟雯瑾，罗成新

(沈阳师范大学 数学与系统科学学院， 沈阳 110034)

具有截断控制参数学习效应及退化效应加工时间依赖于资源的单机排序问题

翟雯瑾，罗成新

(沈阳师范大学 数学与系统科学学院， 沈阳 110034)

讨论具有截断控制参数学习效应和退化效应且工件的加工时间依赖于资源分配的单机排序问题。在凸资源消费函数条件下研究问题，每个任务有一个松弛工期窗口，任务的实际加工时间依赖于截断控制参数、工件的开始加工时间。分别考虑了在工件的提前惩罚、延误惩罚等费用受限的前提下，最小化资源费用；资源消耗总费受限的前提下，使带有提前、延误、交货期开始时间、交货期大小、最大完工时间及总完工时间加权和最小的单机排序问题。将问题转化为指派问题，证明了该问题是在多项式时间内可解的，并分别给出了两个多项式时间的最优算法，并给出了一个算例。

排序；资源分配；截断控制参数；退化效应；指派问题

经典排序中，任务的加工时间是固定的常数，但在实际生产中，任务等待或机器等原因都会引起任务加工时间的增长，即任务的实际加工时间与该任务的开始加工时间有关。然而考虑到学习效应、退化效应、资源分配等情况，任务的加工时间不再是固定不变的。通常情况下，给任务分配一定额度资源，任务的加工时间变小。文献[2]讨论了带有学习和退化效应的单机排序问题，目标函数包括提前、延误和工期的总费用。由于实际生产活动中的需要，带有资源分配的问题逐渐引起关注，文献[3-5]研究了关于资源分配的单机排序问题。文献[6]在工件的加工时间与学习指数相关的凸函数下，研究了工件提前、延迟的工期指派问题。文献[8-13]讨论了带有提前、延误的工期指派问题。文献[14]研究了具有截断控制参数学习效应和退化效应且工件的加工时间依赖于资源分配的单机排序问题，并求得最大加工时间与总完工时间最小值时的最优算法，本文与文献[14]的差别在于目标函数不同。文献[15]研究了具有维护活动及公共工期的加工时间依赖资源的单机排序问题。

在大多数排序模型中，往往以最小化所需费用为首要目标。但在实际生产过程中，有时即便使得总费用最小，也不能满足生产者对费用的预估最小值。因此生产者常常会事先给定预算以限制总费用。文献[1]与文献[11]研究了多种工期下资源受限的单机排序问题，并给出了在总费用受限的前提下资源总数的最优算法。

本文在上述两篇文献的基础上，研究了两个问题。第一个问题是在资源消耗总费用受限的前提下，使带有提前、延误、交货期开始时间、交货期大小、最大完工时间及总完工时间加权和最小单机排序问题。第二个问题是在带有提前、延误、交货期开始时间、交货期大小、最大完工时间及总完工时间加权和受限的前提下，求得总资源消耗费用最小的单机排序问题。在两个问题中，工件的实际加工时间是关于位置与资源的具有截断参数学习效应与退化效应的线性函数与凸函数，通过将问题转化为指派问题得到了多项式时间的最优算法。

1 问题描述

考虑如下的问题：n个独立且在零时刻到达的工件N={J1,J2,…,Jn}，需要在一台机器上加工，在同一时刻机器最多只能加工一个工件，工件必须连续加工不允许中断。在本文中，考虑两种资源分配，分别为退化效应与具有截断控制参数的学习效应模型。在许多资源分配的问题中，普遍采用线性资源消耗函数与凸资源消耗函数。本文里凸资源消耗函数模型中工件的实际处理时间表达式为

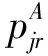
其中α>0,β>0,γ>0,δ1≥0,δ2≥0,μ≥0为给定常数。

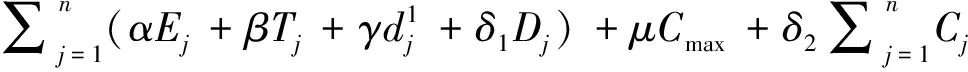
其中α,β,γ,δ1,δ2,μ意义同上，Gj(>0)为资源分配的单位费用。使用文献[7]三参数表示法可将上述问题分别表示为

(1)

(2)

2 问题的最优解

2.1 重要结论

引理1 对于任意给定的排序π=(J[1],J[2],…,J[n])，存在最优的q1和q2，分别是第k个和第l个工件的完工时间(l≥k)，即

证明详细证明见参考文献[1]。

引理2 引理1中的k,l由以下两式确定：q1=C[k]，k=[n(δ1-γ)/α]，q2=C[l]，l=[n(β-δ2)/β]。其中[x]表示不超过x的最大整数。

证明详细证明与参考文献[1]中证明类似。证毕。

引理3 给定排序π=(J[1],J[2],…,J[n])，问题(1)与问题(2)中工件J[k](k=1,2,…,n)的实际加工时间为

(3)

证明 详细证明与参考文献[14]中证明类似。证毕。

由此可以得出

(4)

其中

(5)

Ω1=ω1+cω2+c(1+c)ω3+…+c(1+c)n-2ωn

Ω2=ω2+cω3+c(1+c)ω4+…+c(1+c)n-3ωn

Ω3=ω3+cω4+c(1+c)ω5+…+c(1+c)n-4ωn

………………

Ωn-1=ωn-1+cωn

Ωn=ωn

(6)

2.2 最优算法

引理4 问题(1)中给定工件的排序π=(J[1],J[2],…,J[n])可以得到最优资源分配

(7)

证明 详细证明与参考文献[14]中证明类似。证毕。

将式(7)代入Z1(π,u*)，得到

Z1(π,u*)=U-l

(8)

其中Ωj由(6)决定。

为了求出式(13)最小值，考虑下述指派问题。令

(9)

则转化为如下指派问题：

(10)

(11)

(12)

xjr=0或1j,r=1,2,…,n

(13)

因此，对于问题(1)可以给出如下最优算法。

算法1

第一步 根据引理2，计算出k与l；

第二步 根据式(9)计算出νjrj,r=1,2,…,n；

第三步 求解指派问题(10)～(13)，得到最优排序π*=(J[1],J[2],…,J[n])；

定理1 对于问题(1)可以通过求解指派问题在O(n3)时间内得到最优解。

证明上述分析保证了定理结论的正确性。算法1中的第一、四、五步可以在O(1)时间内完成，第二、三步需要O(n3)时间内完成，所以算法的时间复杂性为O(n3)。证毕。

引理5 问题(2)对于给定的排序π=(J[1],J[2],…,J[n])可以得到最优资源分配

(14)

证明 对于给定排序π=(J[1],J[2],…,J[n])，拉格朗日函数如下：

(15)

其中λ为拉格朗日乘子。对式(20)中的变量分别求偏导,令其为零。得到最优解的充分必要条件

(16)

j=1,2,…,n

(17)

由式(21)和式(22)得到

(18)

(19)

由式(23)和式(24)得到式(19)。证毕。

将式(19)代入Z2π,u*，得到

Z2(π,u*)=

(20)

其中Ωj由式(6)决定。

为了求出式(25)最小值，我们将问题(2)化为指派问题。令

(21)

考虑指派问题

(22)

(23)

(24)

xjr=0 或 1j,r=1,2,…,n

(25)

算法2

第一步 根据引理2，计算出k与l；

第二步 根据式(21)计算出τjrj,r=1,2,…,n；

第三步 求解指派问题(22)～(25)，得到最优排序π*=(J[1],J[2],…,J[n])；

定理2 对于问题(2)可以通过求解指派问题在O(n3)时间内求得最优解。

证明证明过程与定理1证明过程类似。此处省略。证毕。

下面给出问题(1)与问题(2)各一个实例，说明算法的运算过程。

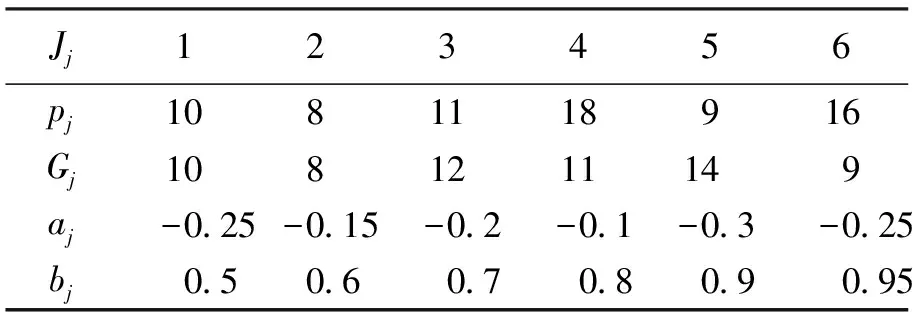
表1 例1的数据

表2 例1中vjr值

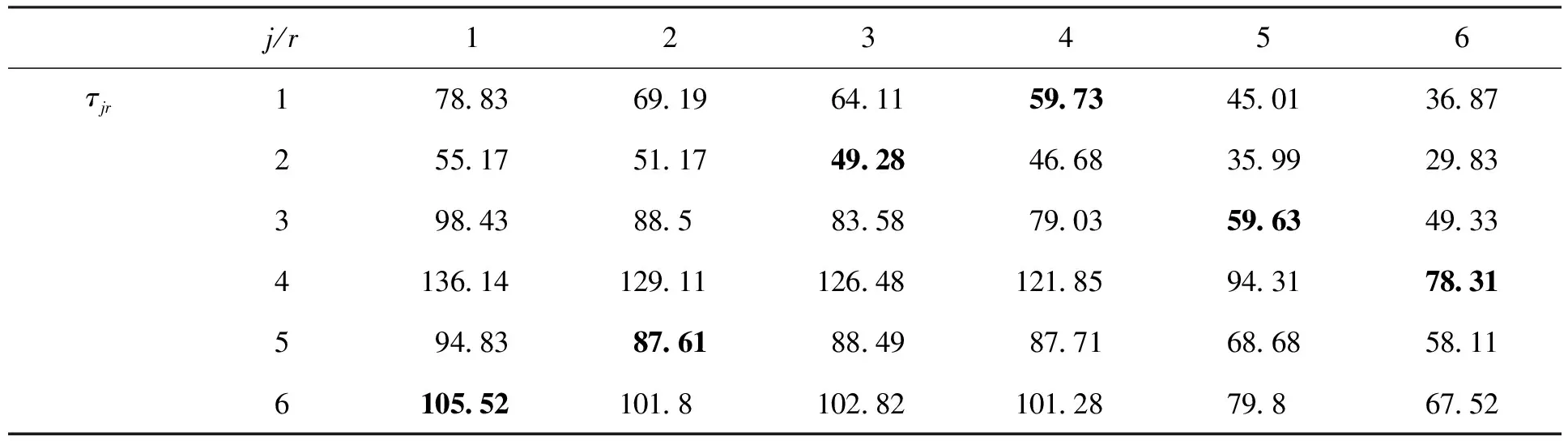
表3 例2中τjr值

3 结论

本文研究了具有截断控制参数的单机排序问题。加工时间是关于资源的凸函数，分别给出目标函数求得最小值的最优算法并证明问题是多项式时间内可解的。在工件的提前惩罚、延误惩罚等总费用和受限的前提下，最小化资源费用的单机排序问题，确定最优资源分配，通过将问题转化为指派问题，证明问题在多项式时间内是可解，并给出了多项式时间算法。

[1] LI GANG,LUO MEILING,ZHANG WENJIE,et al.Single-machine due-window assignment scheduling based on flow allowance,learning effect and resource allocation[J].International Journal of Production Research,2015,53(4):1228-1241.

[2] WANG JIBO，GUO QIAN.A due-date assignment problem with learning effect and deteriorating jobs[J].Appl Math Model,2010,34(2):309-313.

[3] LU Y Y,LI G,WUB,et al.Optimal due-date assignment problem with learning effect and resource-dependent processing times[J].Optimization Letters,2014,8(1):113-127.

[4] WANG X Y,WANG J J.Single-machine due-date assignment problem with deteriorating jobs and resource-dependent processing times[J].International Journal of Advanced Manufacturing Technology,2013,67(1-4):255-260.

[5] WANG J B,WANG J J.Research on scheduling with job-dependent learning effect and convex resource-dependent processing times[J].International Journal of Production Research,2015,53(19):1-11.

[6] WANG JIBO,WANG JIANJUN.Research on scheduling with job-dependent learning effect and convex resource-dependent processing times[J].Int J Pro Res,2015,53(19):5826-5836.

[7] GRAHAM R L,LAWLER E L,LENSTRA J K,et al.Optimization and approximation in deterministic sequencing and scheduling:A survey[J].Annals of Discrete Mathematics,1979,5(1):287-326.

[8] BAKER K R,SCUDDER G D.Sequencing with earliness and tardiness penalties:a review[J].Oper Res,1990,38(1):22-36.

[9] GORDON V S,TARASEVICH A A.A note:Common due date assignment for a single machine scheduling with the rate-modifying activity[J].Comput Oper Res,2009,36(2):325-328.

[10]BISKUP D,JAHNKE H.Common due date assignment for scheduling on a single machine with jointly reducible processing times[J].Int J Prod Econ,2001,69(3):317-322.

[11]SHABTAY D,STEINER G.The single-machine earliness-tardiness scheduling problem with due date assignment and resource-dependent processing times[J].Ann Oper Res,2008,159(1):25-40.

[12]KUO W H,YANG D L.A note on due-date assignment and single-machine scheduling with deteriorating jobs[J].J Oper Res Soc,2008,59(6):857-859.

[13]YANG S J,LEE H T,GUO J Y.Multiple common due dates assignment and scheduling problems with resource allocation and general position-dependent deterioration effect[J].International Journal of Advanced Manufacturing Technology,2013,67(1-4):181-188.

[14]WANG J B,LIU M Q,YIN N,et al.Scheduling jobs with controllable processing time,truncated job-dependent learning and deteriorations effects[J].Journal of Industrial and Management Optimization 2017,13(2):1025-1039.

[15]隋楠，罗成新.具有维护活动及公共工期的加工时间依赖资源的单机排序问题[J].沈阳航空航天大学学报，2016,33(6):90-96.

[16]王吉波，刘璐，许扬涛，等.具有恶化工件的不同工期指派问题研究[J].沈阳航空航天大学学报，2013,30(5):83-87.

[17]王吉波,汪佳,牛玉萍.具有学习效应的单机可控加工时间排序问题研究[J].沈阳航空航天大学学报 2014,31(5):82-86.

[18]王吉波,郭苗苗，刘桓，等.具有依赖开工时间恶化工件的流水作业排序问题研究综述[J].沈阳航空航天大学学报 2016,33(3):1-10.

Singlemachineschedulingproblemwithprocessingtimeofajobdependenttruncatedcontrollearningeffectanddeteriorationeffectandresource

ZHAI Wen-jin,LUO Cheng-xin

(School of Mathematics and System Science,Shenyang Normal University,Shenyang 110034,China)

We study a single machine scheduling problem with truncated job-dependent learning effect and deterioration effects and processing time dependent on resource.The actual processing time of a job is a convex function of the resource amount allocated to it.Each job has a slack due-window.The actual processing time of each job depends on a truncated control parameter,the starting time and the resource amount allocated to it.Two single scheduling problems are studied.The first is to minimize total cost of early and tardy job,the start time,size of each due-window,makespan and total completion time,assume that total resource is limited by a given constant.The second is to minimize the total resource cost under the condition that a total objective value is limited by a given constant.We show that the problem is polynomial solvable by transforming this it into an assignment problem.Two polynomial time optimal algorithms are presented.An example is given to show the algorithm.

scheduling;resource allocation;truncated control parameter;deterioration effect;assignment problem

2017-07-04

辽宁省教育厅项目(项目编号：L2014433)

翟雯瑾(1993-),女,辽宁鞍山人,硕士研究生，主要研究方向：组合最优化，E-mail:724482159@qq.com;罗成新(1958-),男,辽宁新宾人，教授,博士,主要研究方向：组合最优化,E-mail:luochengxin@163.com。

2095-1248(2017)05-0086-06

Q221.7

A

10.3969/j.issn.2095-1248.2017.05.013

(责任编辑：刘划 英文审校：刘勇进)